基于白噪声的网络传染病模型动力学分析*

曹晓春， 荆文君， 靳 祯

（1. 山西财经大学 应用数学学院，太原 030006；2. 山西财经大学 统计学院，太原 030006；3. 山西大学 复杂系统研究所，太原 030006）

引 言

网络传染病学是传染病学的一个分支，近年来受到越来越多的关注，已取得了丰富的成果[1].其中应用最为广泛、成果相对集中的一类模型是 Pastor-Satorras 和 Vespignani 提出的无标度网络传染病模型[2].该模型把人看作社交网络的节点，人与人之间的相互接触看作有边相连，一个人在单位时间内接触的人数是网络中节点的度，按照节点的度将人分为若干组，用Sk和Ik分别表示网络中度为k的易感者和染病者的密度，且假设网络中人数保持不变，即Sk+Ik=1，建立了 SIS(susceptible-infected-susceptible) 传染病模型，其具体形式为

在实际传染病流行过程中，流行病系统在其演变时会受到各种形式的随机干扰.可把随机干扰大致分成两类：一类是许多独立的、细小的随机干扰的总和，这种干扰在数学上通常用白噪声来描述；另一类是数量虽少但强度较大的随机干扰，一般可以用连续时间的 Markov 链或半 Markov 链来描述，亦称之为色噪声.关于色噪声对传染病的影响，已经取得了丰富的成果[4-8]，结果表明，Markov 链的稳态分布对传染病传播有非常重要的影响，既可以抑制也可以加速传染病传播.关于白噪声对传染病的影响，也有许多杰出的工作和成果[9-13].张丽娟等建立了一类潜伏期具备传染性的传染病传播模型，求得了基本再生数，给出了系统稳定性条件[9].Gray 等分析了具有固定人口的随机 SIS 传染病模型，得出了传染病随机持久和灭绝的充分条件，并得到了在传染病持久的情形下染病者数量的稳态分布[10].Lin 等研究了带接种的随机 SIS 传染病模型的平稳分布，证明了模型解的分布密度在适当的条件下能收敛到一个不变密度[11].Miao 等研究了一类具有垂直传播的随机 SIR模型的阈值动力学[12].Chang 等提出了一种具有两种不同的非线性发病率的随机 SIRS 传染病模型，并给出了一种获得随机传染病模型阈值的数学方法[13].前面提到的研究，以及现有文献中绝大多数的研究，是基于传统均匀混合的“仓室”传染病模型，而对描述传染病更加精确、合理的复杂网络传染病模型，这方面的研究还很鲜见.鉴于此，本文将讨论白噪声对复杂网络上的传染病传播动力学的影响，以丰富和补充网络传染病动力学的建模方法和理论分析.

本文结构安排如下：第 1 节建立了复杂网络上的随机 SIS 传染病模型并分析了模型全局正解的存在性和唯一性；第 2、3 节分别给出了传染病随机灭绝和随机持久的充分条件，并分析了其动力学性态；第 4 节数值模拟验证了本文的理论结果；第 5 节给出了本文的结论.

1 随机网络传染病模型

从而 τ+∞=+∞，a.s..证毕.

2 传染病随机灭绝

此处

由条件 (7) 可得

这就意味着

根据Martingale 的强大数定律

由上式和命题(12)得证.

在定理 2 中要求噪声强度 σ2≤λ2/，下面的定理则包含了 σ2>λ2/的情形.

定理3 若

则对任意给定不全为零的初值Ik(0)∈(0,1),k=1,2,···,n，模型 (2) 的解满足

与定理 2 的证法相同，易知

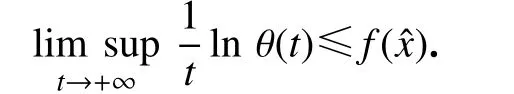
从而命题得证.

3 传染病随机持久

下面将讨论在白噪声影响下网络传染病模型 (2) 随机持久的充分条件.

定理4 若

且

此处

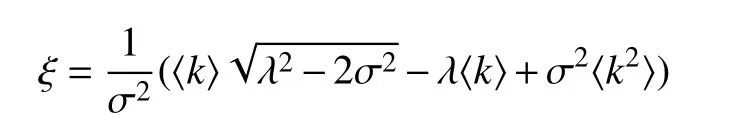
是方程

当 ξ ∈(0,〈k2〉) 时，

于是有

的情形，本文没有从理论上证明传染病动力学行为，传染病在此种情况下既可能随机持久也可能随机灭绝.下一节中将数值模拟在给定时间内传染病随机持久这一情形.

4 数 值 模 拟

本节进行了一些数值模拟，以验证第 2 节和第 3 节中的理论结果，假设所有参数均已适当地单位给出.我们选取了最大度为 30 的网络，其度分布服从参数为 8 的Poisson 分布，度的一阶矩 〈k〉=8.002 7，二阶矩〈k2〉=72.024 2.用 MATLAB 数值模拟，时间步长 ∆=0.001.

图1 参数为 λ=0.1,σ=0.08, 从而RD0=0.9<1,RS0=0.640 8<1, σ2=0.006 4<λ2/RD0=0.011 1. 且 图1 (a)Ik(0)=0.5,图1(b)Ik(0)=0.8,k=1,2,···,n. 图1 表明，在条件 (7) 下，给定任意初值，模型 (2) 的解以指数速度趋于零，即传染病以概率 1 指数灭绝，定理 2 得到验证.

原料：大米 25 g，黑米 25 g，大豆 25 g，红豆 25 g，核桃仁 25 g，花生 25 g，红枣 15 g，桂圆 10 g（2人份）。

图1 不同初值下，确定性模型(1)灭绝情形与随机性模型(2)灭绝情形的I(t)路径模拟：(a) 初值Ik(0)=0.5；(b) 初值Ik(0)=0.8Fig. 1 For different initial values, I(t) path simulations of the extinction case of deterministic model (1) and the extinction case of stochastic model (2):(a) initial value Ik(0)=0.5；(b) initial value Ik(0)=0.8

图2 (a) 参数为 λ=0.1,σ=0.15,Ik(0)=0.5,k=1,2,···n，从而RD0=0.9<1,RS0=−0.011 2<1, 又 σ2=0.022 5，λ2/RD0=0.011 1,λ2/2=0.005, 此时 σ2>λ2/RD0成立.图2 (b) 参数为 λ=0.23,σ=0.6,Ik(0)=0.5,k=1,2,···,n, 从而RD0=2.07>1,RS0=−12.51<1, 又 σ2=0.36,λ2/R0D=0.025 6,λ2/2=0.026 5, 此时 σ2>λ2/2 成立.图2 表明，条件 (13) 暗示了RS0<1，给定初值，随机模型 (2) 的解以指数速度趋于零，验证了定理 3 的理论结果.值得注意的是图2(b)，对确定性模型 (1)，RD0>1, 传染病持久形成地方病，但在白噪声影响下，随机模型 (2) 的RS0<1，传染病随机灭绝，大的噪声可以让原本持久的传染病灭绝，说明白噪声起到抑制传染病传播的作用.

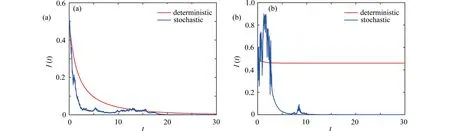
图2 确定性模型(1)灭绝(持久)情形与随机性模型(2)灭绝情形的I(t)路径模拟：(a) 确定性模型(1)灭绝情形与随机性模型(2)灭绝情形；(b) 确定性模型(1)持久情形与随机性模型(2)灭绝情形Fig. 2 I(t) path simulations of the extinction (persistence) case of deterministic model (1) and the extinction case of stochastic model (2): (a) the extinction case of deterministic model (1) and the extinction case of stochastic model (2); (b) the persistence case of deterministic model (1) and the extinction case of stochastic model (2)

图3 参数为 λ=0.4,σ=0.2, 从而RD0=3.6>1,RS0=1.98>1.又图3(a)中Ik(0)=0.5，图3(b)中Ik(0)=0.8,k=1,2,···,n.图3 表明，在条件 (15) 下，给定任意初值，随机模型 (2) 的解是持久的，即传染病以概率 1 随机持久，定理 4 得到验证.

图3 不同初值下，确定性模型(1)持久情形与随机性模型(2)持久情形的I(t)路径模拟：(a) 初值Ik(0)=0.5；(b) 初值Ik(0)=0.8Fig. 3 For different initial values, I(t) path simulations of the persistence case of deterministic model (1) and the persistence case of stochastic model (2):(a) initial value Ik(0)=0.5；(b) initial value Ik(0)=0.8

图4 参数为 λ=0.32,σ=0.225, 从而RD0=2.880 0>1,RS0=0.829 7<1, 且 σ2=0.050 6,λ2/RD0=0.035 6,λ2/2=0.051 2, 满足 λ2/RD0<σ2<λ2/2，又图4(a)中Ik(0)=0.01，图4(b)中Ik(0)=0.1,k=1,2,···,n.图4 模拟了RS0<1且λ2/R<σ2<λ2/2 的情形，给定任意初值，模型 (2) 的解在给定区间上是随机持久的.

图4 不同初值下，确定性模型(1)与随机性模型(2)的I(t)路径模拟图：(a) 初值Ik(0)=0.01；(b) 初值Ik(0)=0.1Fig. 4 For different initial values, I(t) path simulations of deterministic model (1) and stochastic model (2): (a) initial value Ik(0)=0.01;(b) initial value Ik(0)=0.1

5 结 论

本文在网络传染病模型 (1) 中考虑了随机因素，构建了随机网络传染病模型 (2)，证明了模型 (2)存在全局唯一的正解，利用随机微分方程理论得到了传染病随机灭绝和持久的充分条件.当RS0≤1 时，在适当的条件下，传染病将随机灭绝(定理 2 和定理 3)；当RS0>1 时，传染病将随机持久(定理 4).值得注意的是RS01)的传染病灭绝.因此，白噪声在网络传染病传播过程中起着不可忽视的作用，也表明随机模型 (2) 的建立是非常有意义的.最后，通过数值模拟验证了本文的理论结果.

参考文献（ References ） ：

［1］靳 祯, 孙桂全, 刘茂省. 网络传染病动力学建模与分析[M]. 北京: 科学出版社, 2014: 1-393. （JIN Zhen, SUN Guiquan, LIU Maoxing.Dynamic Modeling and Analysis of Network Infectious Diseases[M]. Beijing: Science Press,2014: 1-393. （in Chinese））

［2］P ASTOR-SATORRAS R, VESPIGNANI A. Epidemic spreading in scale-free networks[J].Physical Review Letters, 2001, 86（14）: 3200-3203.

［3］W ANG L, DAI G Z. Global stability of virus spreading in complex heterogeneous networks[J].SIAM Journal on Applied Mathematics, 2008, 68（5）: 1495-1502.

［4］C AO X C, JIN Z. N-intertwined SIS epidemic model with Markovian switching[J].Stochastics and Dynamics,2018, 19（4）: 1950031.

［5］C AO X C, JIN Z. Epidemic threshold and ergodicity of an SIS model in switched networks[J].Journal of Mathematical Analysis and Applications, 2019, 479（1）: 1182-1194.

［6］C AO X C, JIN Z, LIU G R, et al. On the basic reproduction number in semi-Markov switching networks[J].Journal of Biological Dynamics, 2021, 15（1）: 73-85.

［7］曹 娟, 任凤丽. Markov切换时滞基因调控网络的均方同步和随机无源同步[J]. 应用数学和力学, 2022, 43（2）: 198-206. （CAO Juan, REN Fengli. Mean-square synchronization and stochastically passive synchronization of delayed gene regulatory networks with Markovian switching[J].Applied Mathematics and Mechanics, 2022, 43（2）: 198-206.（in Chinese））

［8］何 雪晴, 韦煜明. 同时具有logistic 出生和Markov切换的随机SIRS传染病模型的动力学[J]. 应用数学和力学, 2021,42（12）: 1327-1337. （HE Xueqing, WEI Yuming. Dynamics of a class of stochastic SIRS infectious disease models with both logistic birth and Markov switching[J].Applied Mathematics and Mechanics, 2021, 42（12）: 1327-1337.（in Chinese））

［9］张 丽娟, 王福昌, 万永革, 等. 一类潜伏期有传染性的传染病模型动力学分析[J]. 应用数学和力学, 2021, 42（8）: 866-873. （ZHANG Lijuan, WANG Fuchang, WAN Yongge, et al. Dynamic analysis of an epidemic model with infectivity in the incubation period[J].Applied Mathematics and Mechanics, 2021, 42（8）: 866-873.（in Chinese））

［10］G RAY A, GREENHALGH D, HU L, et al. A stochastic differential equation SIS epidemic model[J].SIAM Journal on Applied Mathematics, 2011, 71（3）: 876-902.

［11］L IN Y G, JIANG D Q, WANG S A. Stationary distribution of a stochastic SIS epidemic model with vaccination[J].Physica A:Statistical Mechanics and Its Applications, 2014, 394: 187-197.

［12］M IAO A Q, ZHANG J, ZHANG T Q, et al. Threshold dynamics of a stochastic SIR model with vertical transmission and vaccination[J].Computational and Mathematical Methods in Medicine, 2017, 2017（2）: 1-10.

［13］C HANG Z B, MENG X Z, LU X. Analysis of a novel stochastic SIRS epidemic model with two different saturated incidence rates[J].Physica A:Statistical Mechanics and Its Applications, 2017, 472: 103-116.

［14］Ø KSENDAL B.Stochastic Differential Equations and Applications[M]. New York: Springer-Verlag Heidelberg Press, 2000: 1-332.

［15］M AO X R.Stochastic Differential Equations and Applications[M]. Cambridge: Woodhead Publishing Limited Press, 2011: 1-422.

［16］L I X Y, GRAY A, JIANG D Q, et al. Sufficient and necessary conditions of stochastic permanence and extinction for stochastic logistic populations under regime switching[J].Journal of Mathematical Analysis and Applications, 2011, 376（1）: 11-28.