考虑磁通流动效应的超导薄膜基底结构界面断裂行为研究*
丁洁莹, 薛 峰, 苟晓凡
(河海大学 力学与材料学院,南京 211100)
(我刊编委苟晓凡来稿)
引 言
超导薄膜是一种采用化学涂层制备而成的多层薄膜结构,因其具有极佳的低温高场电性能,广泛应用于电力、交通、医疗等各个领域.对于超导薄膜结构,通常超导层与基底结合界面较为脆弱[1-2].这种超导薄膜界面强度不仅关乎超导薄膜结构的破坏与完整性,更为重要的是,与导电能力密切关联.为此,针对超导薄膜界面裂纹破坏及其影响规律的研究非常必要.截至目前,已有不少针对薄膜基底结构的界面裂纹问题的研究[3-4].Hutchinson 等[5-6]通过理论推导,提出了稳态开裂下双层膜的界面裂纹计算模型,可用于分析裂纹尖端处的应力分布.由于解析方法的局限性,以有限单元法和边界元法为代表的数值解法纷纷涌现[7-8].Ma 和Su 等[9]使用拓展有限元法(X-FEM),解决了静态双材料界面断裂问题;Gu 等[10]提出了基于边界元法的新型裂纹尖端单元,可用于分析复合材料的界面裂纹.以上方法为分析超导薄膜界面处断裂性能提供了帮助.
超导薄膜受到的电磁力是导致其界面发生裂纹破坏的重要因素.Gruss 等[11]观察到外加磁场变化和温度变化都会对薄膜内电磁场产生影响,进而影响超导薄膜所受的电磁力.Zeldov 等[12]对无限长的Ⅱ型超导薄膜的临界状态进行了理论分析,指出磁通穿透区域内电流密度的幅值等于临界电流密度jc.Brandt 和Indenbom等[13]给出了在外部磁场垂直作用下,Ⅱ型超导薄膜在临界状态下的电流密度和总磁场分布.然而,上述方法的临界电流密度都是恒定的,McDonald 等[14]在临界电流密度Jc(B) 任意给定的前提下,分析了无限长Ⅱ型超导薄膜的电磁场.此外,磁通钉扎效应引起磁致伸缩对不同形状的Ⅱ型超导体的应力、应变的影响不容忽视[15-16],Zhao 等[17]考虑了在磁通钉扎效应影响下,通量流动速度对超导薄膜的磁化强度和应力的影响.结合以上方法,考虑磁通钉扎效应的影响,可以更为合理地描述超导薄膜受到的电磁力.
为此,针对超导薄膜,在外磁场作用下,引入了超导磁通钉扎效应所引起的黏性通量流动对于薄膜结构电磁力的影响,并优化了电磁力计算方法,深入研究了磁通流动速度对薄膜基底结构界面裂纹的影响.
1 计算模型与公式
1.1 计算模型
如图1(a)所示,长L、宽2a的超导薄膜(1#)被沉积在基底(2#)上,厚度分别为h1和h2,且满足h1≪h2.超导薄膜和基底之间的界面与y轴重合,在界面上存在初始裂纹.问题满足以下假设:超导薄膜和基底都是各向同性和线弹性的;初始裂纹长度为超导膜厚度的数倍,初始裂纹尺寸不影响裂纹开裂;2a≪L,问题满足平面应力条件.
在垂直于超导薄膜、平行于z轴方向施加密度为Ba的外加磁场,图1(b)为超导薄膜内电磁力分布的示意图,在临界状态下,磁通Bz垂直于xOy平面穿透超导薄膜,使得超导薄膜内产生密度为jc的矩形环状电流,同一个电流环上的任意点到外部边界的距离相等[15].屏蔽区对应薄膜内磁场强度为零的区域,图中 2b对应屏蔽区的宽度, 2b˜为薄膜内电磁分布的另一个间断点,满足a>b˜>b.由于电流回路的特性,可以将薄膜划分成四个区域.为了便于描述薄膜内的电磁场分布,选取横截面A,截面A 满足y=L/2 且平行于xOz平面.

图1 计算模型示意图: (a) 超导薄膜/基底结构界面裂纹问题;(b) 电磁力分布Fig. 1 The schematic drawing for calculation: (a) interface crack between superconducting thin film and substrate; (b) electromagnetic force distribution
1.2 电磁场公式
场冷和零场冷是使得Ⅱ型超导体内产生俘获磁场的两种常用方法.场冷指的是超导体在一个固定的外加磁场中冷却,最后撤去外加磁场的过程;零场冷指的是先冷却然后再施加外加磁场,最后撤去外加磁场的过程.这两种方法在超导体内产生的俘获磁场分布不同,与路径有关[18].本文研究零场冷的磁化过程.

当外加磁场和临界电流给定时,可由上式解出屏蔽区域尺寸b.
根据式(2),可将式(1)与式(3)结合,得到考虑通量流动速度的屏蔽区尺寸的表达式为

超导膜内的电流密度分布和磁通密度分布如下[14]:
1) 磁场上升阶段

超导膜内的电流密度和磁通密度分布明确后,磁化过程的电磁体力可以通过f=j×B得到.由于垂直于yOz平面的力fx对沿y轴的裂纹几乎没有影响,因此我们只考虑fy:

1.3 断裂公式

需要说明的是,如图2 所示,如果裂纹在界面中间且关于中轴对称,则可以将问题简化为图1(a)的简化计算模型[6],此时断裂公式(11) ~ (17)依旧可用,注意需要满足前面部分所作的假设:h1≪h2,2a≪L且初始裂纹长度为薄膜厚度的数倍.

图2 薄膜与基底结构界面中心处裂纹计算模型示意图Fig. 2 The calculation model of a crack at the center of the interface between the thin film and the substrate
2 结果与讨论
2.1 磁场上升阶段薄膜内电磁场分布
当外加磁场Ba/Bp=2时,截面A 的电流密度和磁通密度分布分别如图3、图4 所示,为了清楚地反映变化趋势,选定磁通流动速度v0/a=0 s−1, 0.5 s−1,3 s−1.由图3 可知,随着磁通流动速度的增大,膜内电流密度的最大值将会增大,并且电流密度分布的变化速率加快,这意味着维持膜内最大电流密度的能力变弱.从图4 可以看出,随着磁通流动速度的增大,磁通密度的极值随之增大.此外,注意到图4 薄膜内磁通密度为零对应的x轴范围为屏蔽区的尺寸,即图1(b)中所示的2b,较大的磁通流动速度将会导致较大的屏蔽区尺寸.
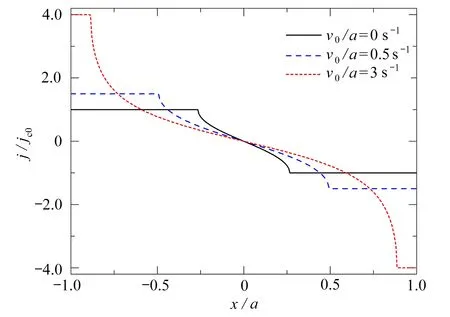
图3 截面A 的电流密度分布 (磁场上升阶段)Fig. 3 The current density distribution in cross-section A (the increasing field)

图4 截面A 的磁通密度分布 (磁场上升阶段)Fig. 4 The flux density distribution in cross-section A (the increasing field)
进一步可以得到,当磁通流动速度增大时,非零的电磁力将会向膜边缘集中,且电磁力最大值将增大.
2.2 磁场上升阶段裂尖应力场
图5 和图6 分别给出了Ⅰ型应力强度因子和Ⅱ型应力强度因子与外加磁场的关系.Ⅰ型应力强度因子表示裂纹尖端处法向正应力的强度,Ⅱ型应力强度因子则表示裂纹尖端处切应力的强度.图5 和图6 表明,随着外加磁场逐渐增大,裂纹尖端处的正应力和切应力均增大.在外加磁场不变的情况下,磁通流动速度越大,裂纹尖端处正应力和切应力越大,且切应力的增量相对于正应力更大一些.此外,较大的磁通流动速度将会导致裂尖应力场的变化速率加快.

图5 Ⅰ型应力强度因子KI/K0 与外加磁场的关系(磁场上升阶段)Fig. 5 The relationship between mode Ⅰ stress intensity factor KI/K0 and the magnetic field (the increasing field)

图6 Ⅱ型应力强度因子KⅡ/K0 与外加磁场的关系(磁场上升阶段)Fig. 6 The relationship between mode Ⅱ stress intensity factor KⅡ/K0 and the magnetic field (the increasing field)
通过以上分析可以得到,磁通流动速度和裂纹尖端处的应力是正相关的,且磁通流速变化对切应力的影响更大.
2.3 磁场下降阶段薄膜内电磁场分布
当Ba/Bp=1.5时,截面A 的电流密度和磁通密度分布分别如图7、图8 所示.如图7 所示,电流密度分布关于零点反对称,在x轴正方向,电流密度从零点开始先增大至极大值,后减小至极小值随后保持恒定,两个极值对应的x轴坐标分别是b和b˜.图7 表明,磁通流动速度的增大将会导致膜内电流密度的最大值增大,电流密度分布的变化速率也将提高,同时电流密度的分布将会更加靠近薄膜边缘.如图8 所示,磁通密度分布关于截面A 的中轴对称,与电流密度分布一致,磁通密度分布也存在两个分段点.图8 表明,磁通密度峰值的大小会随着磁通流动速度的增大而增大.此外,磁通流动速度的增大会导致磁通密度分布更加接近薄膜边缘.

图7 截面A 的电流密度分布 (磁场下降阶段)Fig. 7 The current density distribution in cross-section A(the decreasing field)

图8 截面A 的磁通密度分布 (磁场下降阶段)Fig. 8 The flux density distribution in cross-section A(the decreasing field)
将上述内容与磁场上升阶段的相关内容进行对比,可以得出:超导薄膜在外加磁场的作用下,磁通流动速度越大,膜内屏蔽区尺寸就越大,同时薄膜内电流密度的极值和变化速率也将增大,磁通密度分布同理.相对于磁场上升阶段,上述变化在磁场下降阶段更为明显.
2.4 磁场下降阶段裂尖应力场
Ⅰ型应力强度因子和Ⅱ型应力强度因子与外加磁场的关系分别如图9、图10 所示.由于裂纹面正向压应力对裂纹张拉破坏没有影响,也就是说KI/K0取负值没有意义,因此将负的KI/K0取为零.由图9 和图10 可知,磁通流动速度的增大,会导致裂纹尖端的应力(正应力和切应力)增大,以及应力场的变化速率加快.需要注意:大约在外加磁场Ba/Bp<1 的区域内,裂纹尖端正应力为零,切应力为负,磁通流动速度的增大将会减小出现这一现象的Ba/Bp的范围.结合式(10)、(15)可以得到,裂纹尖端应力为负值是由于此时作用在裂纹边缘处的合力 σu为负值造成的,这对应了超导薄膜两端受拉的情况.

图9 Ⅰ型应力强度因子KI/K0 与外加磁场的关系(磁场下降阶段)Fig. 9 The relationship between mode Ⅰ stress intensity factor KI/K0 and the magnetic field (the decreasing field)

图10 Ⅱ型应力强度因子KⅡ/K0 与外加磁场的关系(磁场下降阶段)Fig. 10 The relationship between mode Ⅱ stress intensity factor KⅡ/K0 and the magnetic field (the decreasing field)
将上述内容与磁场上升阶段的相关内容进行对比,可以得出:随着磁通流动速度的增大,裂纹尖端场的应力(正应力和切应力)将会增大,且变化速率加快.特别是在磁场下降阶段中,当外加磁场的取值为靠近零点的一个小范围时,会出现裂纹尖端处拉应力为零且剪应力为负值的现象,磁通流动速度的增大将减小这个范围.
2.5 能量释放率
图11 展示了不同的磁通流动速度下,能量释放率G与外加磁场强度Ba的关系,用不带标记的线和带标记的线分别表示磁场上升阶段和磁场下降阶段.从图11(a)可以看出,磁场上升和下降阶段都在Ba=Bm时达到G的最大值.相同外部条件下,磁通流动速度越大会导致能量释放率越大,这意味着裂纹开裂的风险增大.大多数时候磁场上升阶段的能量释放率都大于磁场下降阶段,这意味着最大开裂概率发生在磁场上升阶段.如图11(b)所示,在Ba接近于零点的一个较小范围内,磁场下降阶段中的能量释放率大于上升阶段.需要注意到,在磁场下降阶段中,随着外加磁场的增加,能量释放率有一个先上升至峰值后减小至0 最后继续上升的山形走势,通过增大磁通流动速度,将会使得出现上述山形曲线对应的Ba的范围减小.

图11 磁场上升阶段和磁场下降阶段能量释放率与外加磁场的关系:(a) Ba≤2.0Bp;(b) Ba≤1.2Bp, G/G0≤0.04Fig. 11 The relationship between the energy release rate and the external magnetic field in increasing and decreasing fields:(a) Ba≤2.0Bp; (b) Ba≤1.2Bp, G/G0≤0.04
我们得出,在磁场上升阶段和磁场下降阶段中,能量释放率均在Ba=Bm处均达到最大值.相同条件下,磁通流动速度越大,裂纹开裂的风险就越大,此外,最大开裂概率发生在磁场上升阶段.
3 结 论
为了分析超导薄膜与厚基底在外部磁场作用下的界面裂纹问题,本文基于磁通量子穿透薄膜理论和线弹性断裂理论,建立了研究超导层与基底界面裂纹问题的解析模型,对外加磁场作用下磁通流动速度对裂纹尖端应力场和能量释放率的影响进行了分析.所得结果表明:超导薄膜在外加磁场的作用下,磁通流动速度越大,裂纹尖端处的应力越大,能量释放率也越大,这意味着裂纹开裂的风险越大.本解析模型有助于分析磁通流动效应对薄膜基底结构界面断裂行为的影响,但与超导薄膜的实际应用情况相比仍有差距,例如做出了线弹性假设以及忽略了热应力的影响,因此,今后仍需针对更为复杂的情况进行研究.
参考文献( References ) :
[1]Z HANG Z X, XUE F, GOU X F. Interaction of two parallel cracks in REBCO bulk superconductors under applied magnetic field[J].Chinese Physics Letters, 2016, 33(7): 077401.
[2]高 配峰. 高温超导复合带材力学行为及变形对临界特性影响的研究[D]. 博士学位论文. 兰州: 兰州大学, 2017.(GAO Peifeng. Mechanical behaviors and influence of deformation on critical properties for high temperature superconducting composite tapes[D]. PhD Thesis.Lanzhou: Lanzhou University, 2017. (in Chinese))
[3]M BAM S O, GOU X F. Interface crack growth rate and fatigue life of multilayer-coated conductor tapes[J].Engineering Fracture Mechanics, 2020, 228: 106910.
[4]Y ONG H D, ZHOU Y H. Interface crack between superconducting film and substrate[J].Journal of Applied Physics, 2011, 110(6): 063924.
[5]H UTCHINSON J W, SUO Z. Mixed mode cracking in layered materials[J].Advances in Applied Mechanics,1991, 29: 63-191.
[6]S UO Z, HUTCHINSON J W. Interface crack between two elastic layers[J].International Journal of Fracture,1990, 43(1): 1-18.
[7]李 聪, 牛忠荣, 胡宗军, 等. 求解双材料裂纹结构全域应力场的扩展边界元法[J]. 应用数学和力学, 2019, 40(8): 926-937. (LI Cong, NIU Zhongrong, HU Zongjun, et al. Computation of total stress fields for cracked bi-material structures with the extended boundary element method[J].Applied Mathematics and Mechanics, 2019, 40(8):926-937.(in Chinese))
[8]张 厚源. 考虑层间界面失效行为的REBCO超导层合带材裂纹扩展数值研究[D]. 博士学位论文. 兰州: 兰州大学,2020. (ZHANG Houyuan. Numerical study on crack propagation of REBCO superconducting laminated tapes considering the behavior of interfacial[D]. PhD Thesis. Lanzhou: Lanzhou University, 2020. (in Chinese))
[9]M A P, SU R K L, FENG W J. Crack tip enrichment functions for extended finite element analysis of two-dimensional interface cracks in anisotropic magneto-electro-elastic bimaterials[J].Engineering Fracture Mechanics,2016, 161: 21-39.
[10]G U Y, ZHANG C Z. Novel special crack-tip elements for interface crack analysis by an efficient boundary element method[J].Engineering Fracture Mechanics, 2020, 239: 107302.
[11]G RUSS S, FUCHS G, KRABBES G, et al. Superconducting bulk magnets: very high trapped fields and cracking[J].Applied Physics Letters, 2001, 79(19): 3131-3133.
[12]Z ELDOV E, CLEM J R, MCELFRESH M, et al. Magnetization and transport currents in thin super conducting films[J].Physical Review B, 1994, 49(14): 9802-9822.
[13]B RANDT E H, INDENBOM M V, FORKL A. Type-Ⅱ superconducting strip in perpendicular magnetic field[J].Europhysics Letters, 1993, 22(9): 599-610.
[14]M CDONALD J, CLEM J R. Theory of flux penetration into thin films with field-dependent critical current[J].Physical Review B, 1996, 53(13): 8643-8650.
[15]J OHANSEN T H. Flux-pinning-induced stress and strain in superconductors: long rectangular slab[J].Physical Review B, 1999, 60(17): 11187-11190.
[16]X UE F, YONG H D, ZHOU Y H. Effect of flux creep and viscous flux flow on flux-pinning-induced stress and magnetostriction in a long rectangular slab superconductor[J].Journal of Applied Physics, 2010, 108(10):103910.
[17]Z HAO Y F, XIONG K. Magnetization and stress in superconducting film under electromagnetic force with viscous flux flow[J].Modern Physics Letters B, 2020, 34(26): 2050283.
[18]章 立源, 张金龙, 崔广霁. 超导物理学[M]. 北京: 电子工业出版社, 1995. (ZHANG Liyuan, ZHANG Jinlong, CUI Guangji.Superconductivity Physics[M]. Beijing: Publishing House of Electronics Industry, 1995. (in Chinese))
[19]Y ANG Y, XIAO L Y, LI X H. Impact of viscous flux flow on the stress in long rectangular slab superconductors[J].Journal of Applied Physics, 2010, 107(2): 023910.
[20]E VANS A G, HUTCHINSON J W. The thermomechanical integrity of thin films and multilayers[J].Acta Metallurgica et Materialia, 1995, 43(7): 2507-2530.

