弯曲载荷作用下舱段连接螺栓组载荷数值研究①

姚 琪，尤军峰，吴 敏

(中国航天科技集团有限公司四院四十一所 燃烧、流动和热结构国家级重点实验室，西安 710025)

0 引言

导弹、火箭舱段之间大量使用螺栓连接结构，螺栓连接结构强度是影响火箭结构可靠性的重要因素。1969～1984年，在7种型号发动机的50次试验中，约有18%的故障是由连接结构的问题引起的。为保证舱段之间可靠连接，需要准确研究螺栓的受力载荷情况。

根据《紧固件连接设计手册》中受翻转力矩的螺栓组连接的章节内容，可求得螺栓组的理论工作拉力载荷。然而，由于结构的变形协调，螺栓组实际受力状态和理论计算存在较大的偏差。对于工程结构连接螺栓的受力问题，国内外诸多学者在螺栓及螺栓预紧力方面做了大量研究。张倩等使用ANSYS软件，仿真分析压力容器螺栓连接结构的受力特征，发现有限元方法计算得到的螺栓载荷远大于理论计算结果。邱凯等通过建立导弹关键螺栓连接结构的有限元分析，优化了螺栓预紧力范围。CAO等研究了含有预紧力的环状螺栓法兰受力特点，发现当螺栓工作拉力小于1.1倍预紧力时，螺栓拉力近似为1.1倍预紧力，当螺栓工作拉力大于1.1倍预紧力时，法兰面会分离，螺栓拉力与螺栓工作拉力相等。蒋国庆等建立了螺栓法兰结构的参数化模型，分析得到连接拉伸刚度与开孔半径、法兰厚度、开孔位置等因素的关系。姚星宇等分析了螺栓个数、预紧力、螺杆直径、法兰厚度对航空发动机双层连接结构、三层连接结构的连接刚度的影响。谢雪峰分析了预紧力、螺栓长度、法兰厚度、螺栓位置等因素对拉力作用下法兰连接结构中螺栓载荷的“杠杆效应”和“环状效应”的影响。栾宇等研究了螺栓法兰连接结构的拉压静刚度非线性，分析了航天器的动力学响应。姜运哲等研究了随机激励下螺栓法兰连接结构稳态响应分析。袁彪等研究了弯矩作用下火箭对接面螺栓拉力分布。然而，上述研究仅考虑了螺栓的拉力，忽略了螺栓受到的弯矩载荷、应力、预紧力和对接面张口大小等因素。

本文针对弯曲载荷作用下舱段间连接螺栓组的载荷问题，建立了精确的舱段螺栓连接结构有限元模型，计算分析舱段弯矩作用下的螺栓组的轴拉载荷、弯矩载荷、螺栓应力和舱段对接面张口大小等，并分析螺栓预紧力、螺栓数量、螺栓直径、螺栓分布圆直径、舱段法兰厚度等因素对螺栓连接结构的影响。

1 舱段间连接螺栓组载荷工程理论计算

假定两个舱段对接面始终保持为平面，且在翻转力矩的作用下，舱段有绕螺栓组形心翻转的趋势。翻转面一侧受到拉力载荷，另一侧预紧力减小，相当于受到负的拉力。螺栓的拉力和另一侧相对应的压力都与各自至翻转面的距离成正比。螺栓拉力载荷分布如图1所示。在翻转力矩作用下，螺栓拉力载荷为

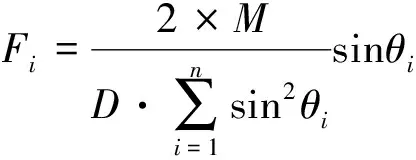
(1)

式中为螺栓个数；为螺栓分布圆直径；为螺栓绕翻转面的角度。

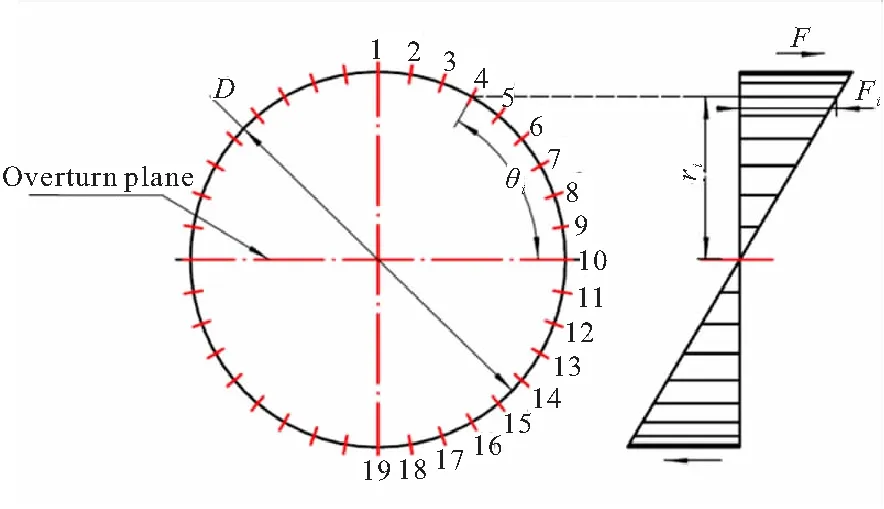
图1 翻转力矩M作用下的螺栓组拉力载荷Fig.1 Loads on bolt-set under the bending moment M

2 舱段间连接螺栓组载荷有限元计算

2.1 几何模型

舱段连接结构包括舱段1、舱段2、36个均布的M8螺栓和螺母，如图2所示。

图2 舱段连接结构Fig.2 Connecting structure for cabins

舱段直径为750 mm，螺栓组的分布圆直径为698 mm，舱段法兰厚度为7 mm，法兰内径为678 mm，舱段长度为300 mm，舱段螺栓和螺母直径按照螺纹小径建模。

舱段1、舱段2、螺栓和螺母的材料均为钢，弹性模量210 GPa，泊松比0.3，密度7850 kg/m。

2.2 有限元模型

使用ABAQUS有限元分析软件，建立舱段连接结构的有限元模型，共有612 904个C3D8R单元，784 041个节点。其中，单个螺栓有5700个单元，单个螺母有1440个单元，如图3所示。

接触设置：在螺栓与舱段1之间、螺母与舱段2之间、舱段1与舱段2之间施加接触约束，共73个接触对，摩擦系数设为0.2。

绑定设置：在螺栓与螺母之间的螺纹接触段，使用绑定设置来模拟，共36个绑定对。

边界条件与载荷设置：在舱段2右端面施加舱段弯矩载荷=-20 000 N·m，在舱段1左端面施加固定约束。

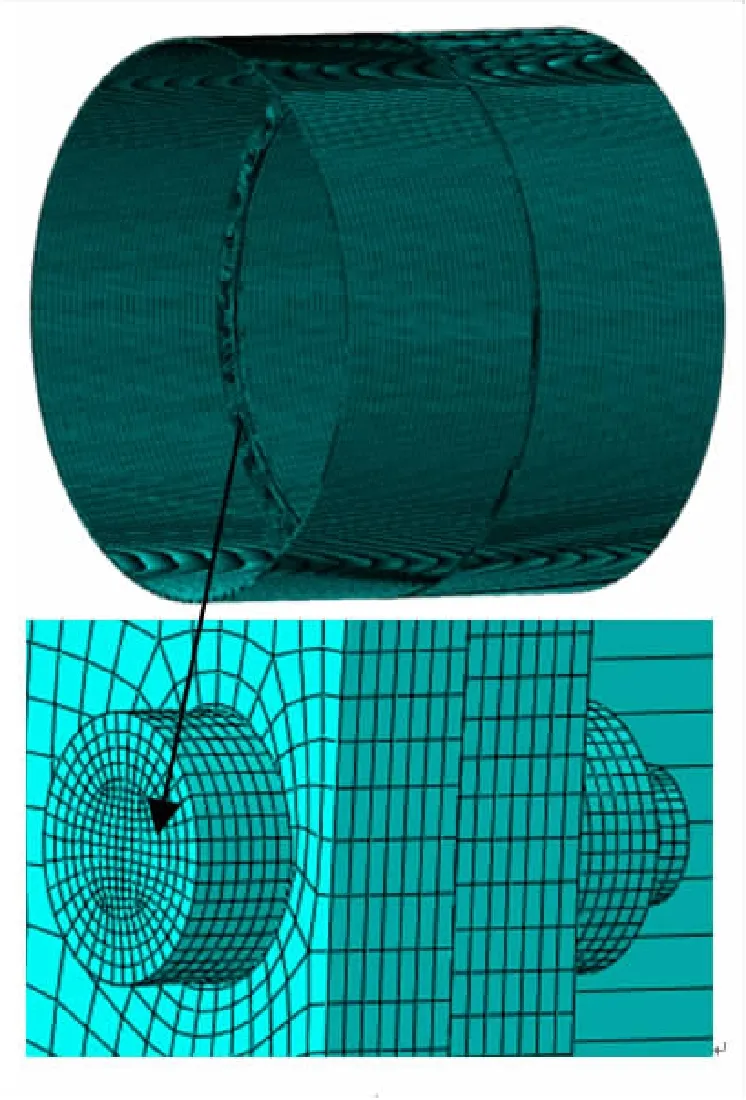
图3 舱段连接结构的有限元模型Fig.3 Computational mesh of connecting structure for cabins

2.3 计算结果

由于结构对称和载荷对称，因此仅对比分析螺栓1～19的载荷(1为顶部受拉螺栓)。

由于有限元计算中考虑了结构变形协调，螺栓既承受轴向载荷，又承受弯矩载荷。以1号螺栓为例，其轴拉载荷和弯矩载荷随舱段弯矩的变化曲线如图4所示。可见，螺栓的轴拉载荷和弯矩载荷随舱段弯矩的增加而近乎线性增加。

图4 1#号螺栓载荷Fs和Mz随舱段弯矩载荷变化曲线Fig.4 Curves of No.1 bolt load Fs and Mz changing with cabin bending moment

螺栓载荷的理论计算结果和有限元计算结果如表1所示。

表1 螺栓组载荷的理论计算和有限元仿真计算结果

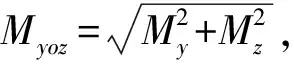
理论计算中螺栓仅受轴向载荷，且螺栓轴向载荷与螺栓距理论翻转面的距离成正比，螺栓最大轴拉载荷为3184 N，发生在距离理论翻转面最远的1号螺栓处，远小于有限元计算结果7875 N。

有限元计算结果中，螺栓1～9的轴拉载荷是理论计算的2.03～2.47倍。螺栓12～19的轴拉载荷较小，几乎为0。螺栓10和螺栓11螺栓的轴拉载荷分别为567.6 N和141.1 N，而对应的理论计算结果分别是0和-553 N。结果表明，螺栓轴拉载荷随着的减小而减小，但是螺栓组的实际翻转面并非理论翻转面，螺栓轴拉载荷与并不是理论计算中假定的正比关系，如图5所示。

(a)Axial tension load distribution diagra (b)Axial tension load bar diagram图5 螺栓组轴拉载荷分布图和柱状图Fig.5 Distribution and bar diagram of axial tension load on bolt-set

理论计算忽略了螺栓所受的弯矩载荷。有限元计算结果中，螺栓弯矩载荷随着螺栓距理论翻转面距离的减小而减小，与螺栓轴拉载荷的分布规律一致，如图6所示。螺栓的最大弯矩载荷为4.724 N·m，发生在距离理论翻转面最远的1号螺栓处。

图6 螺栓组弯矩载荷Myoz分布图Fig.6 Distribution diagram of bending moment(Myoz)on bolt-set

以1号螺栓为例，分析其应力。其轴拉载荷=7875 N，弯矩载荷=4.724 N·m。根据式(2)和式(3)，计算得到螺栓的顶部和底部应力分别为390 MPa和63 MPa。

(2)

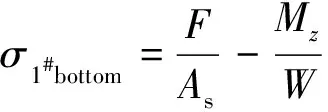
(3)

式中为螺栓横截面面积；为螺栓抗弯模量。

图7为1号螺栓及其螺杆段的Mises应力云图，螺杆段最大Mises应力和最小Mises应力分别为381.9 MPa和73.14 MPa，和上述计算结果一致性较好。

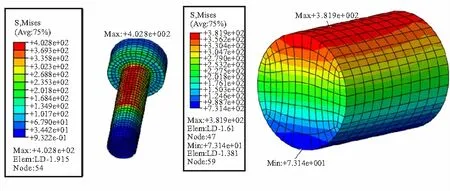
图7 1#号螺栓及其螺杆段Mises应力云图Fig.7 Mises stress contours of No.1 bolt and its rod

结果表明，螺栓弯矩载荷显著增大了螺栓的最大应力。在弹性范围内，同时考虑了螺栓轴拉载荷和弯矩载荷的螺栓等效轴拉载荷，可用来表征螺栓弯矩载荷和轴拉载荷对该螺栓最大应力的影响。以1号螺栓为例，1号螺栓的等效轴拉载荷为13 558 N，最大应力为390 MPa，分别是理论计算轴拉载荷3184 N和应力91.7 MPa的4.26倍。

舱段1与舱段2之间的相互作用力为86 574 N，压心位置为=40.934 2 mm，模型的静力和弯矩平衡。而理论计算中，舱段1和舱段2之间相互作用力为0。

舱段1和舱段2对接面的张口大小分布图如图8所示，与螺栓轴拉载荷和弯矩载荷的分布规律一致。对接面最大张口为0.212 mm，发生在1号螺栓附近，如图8所示。法兰内径处紧密贴合，以此处为支点，螺栓到支点的力臂小于舱壁到支点的力臂，从而产生“杠杆效应”，导致螺栓轴拉载荷的放大。

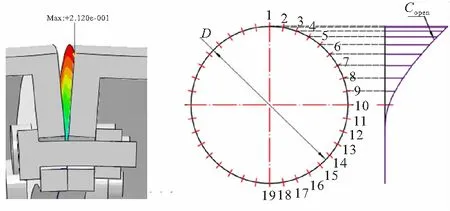
(a)Contact opening contour (b)Contact opening distributiondiagram图8 对接面张口云图及大小Fig.8 Contact opening contours and values of the contact surface

3 螺栓载荷影响因素分析

3.1 预紧力

创建多个分析步，在第1个分析步中，在每个螺栓上施加螺栓预紧力12 500 N；在其余分析步中，将施加的预紧力设置改为“fix at current length”，并分别施加大小为10 000、20 000、25 000、30 000、31 700、40 000、60 000 N·m舱段弯矩载荷-cabin。

19个螺栓轴拉载荷(含预紧力)在不同舱段弯矩载荷作用下的的分布图和折线图，如图9所示。当螺栓轴拉载荷(不含预紧力作用)远小于预紧力时，舱段之间紧密贴合，螺栓轴拉载荷(含预紧力)等于螺栓预紧力；当螺栓轴拉载荷(不含预紧力)接近螺栓预紧力时，舱段之间开始有轻微张口，螺栓轴拉载荷(含预紧力)略大于螺栓预紧力。以1号螺栓为例，当舱段弯矩为31 700 N·m时，其轴拉载荷(含预紧力)为15 520 N，是其轴拉载荷(不含预紧力) 12 500 N的1.24倍；当螺栓轴拉载荷(不含预紧力)大于螺栓预紧力时，舱段之间有较大的张口，螺栓轴拉载荷(含预紧力)近似于螺栓轴拉载荷(不含预紧力)。以1号螺栓为例，当舱段弯矩为60 000 N·m时，其轴拉载荷(含预紧力)为25 580 N，接近于其轴拉载荷23 625 N (不含预紧力)。

(a)Axial load distribution diagram

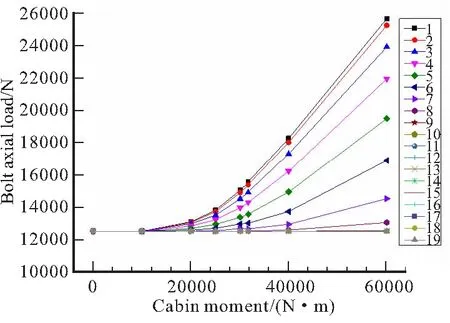
(b)Axial load line chart图9 不同舱段弯矩载荷作用下螺栓轴拉载荷分布图和折线图Fig.9 Distribution diagram and line chart of axial tension load on bolt-set under different cabin bending moment

19个螺栓弯矩载荷(含预紧力)在不同舱段弯矩载荷作用下的分布图和折线图，如图10所示。

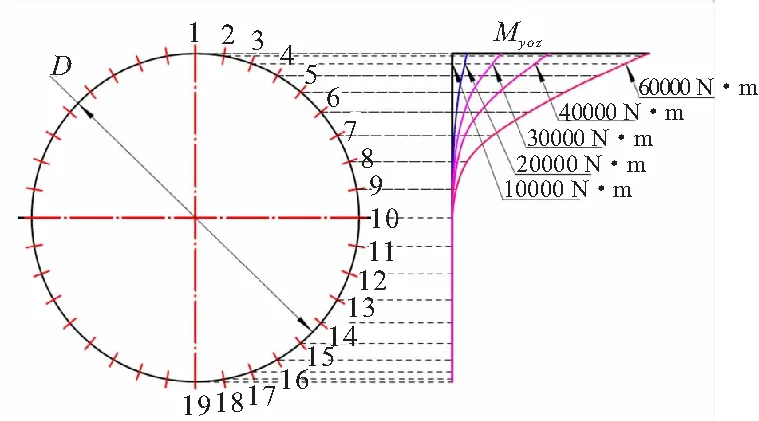
(a)Bending moment distribution diagram

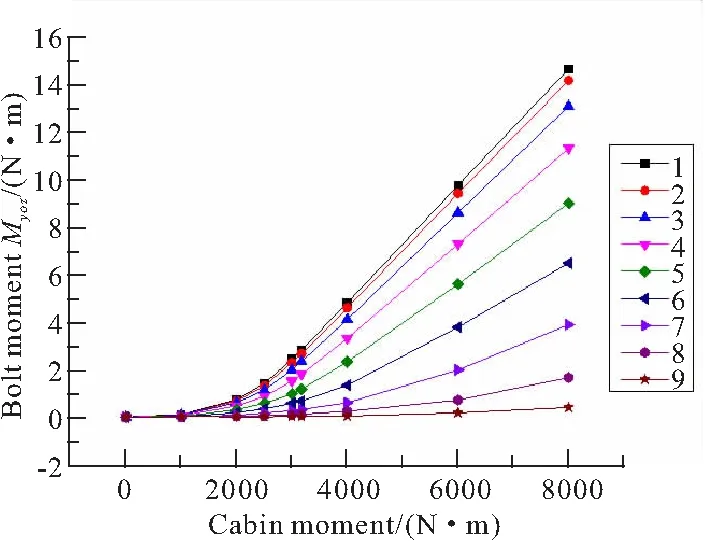
(b)Bending moment line chart图10 不同舱段弯矩载荷作用下螺栓弯矩载荷分布图和折线图Fig.10 Distribution diagram and line chart of bending moment on bolt-set under different cabin bending moment

当螺栓轴拉载荷(不含预紧力)远小于螺栓预紧力时，舱段之间紧密贴合，螺栓弯矩载荷等于0；当螺栓轴拉载荷(不含预紧力)接近螺栓预紧力时，舱段之间开始有轻微张口，螺栓弯矩载荷开始从0缓慢增大；当螺栓轴拉载荷(不含预紧力)大于螺栓预紧力，舱段之间有较大的张口，螺栓的弯矩载荷迅速增大，螺栓弯矩载荷近似于螺栓弯矩载荷(不含预紧力)。

螺栓弯矩载荷会显著增大螺栓最大应力。因此，在设计螺栓预紧力时，须确保螺栓预紧力大于螺栓轴拉载荷(不含预紧力)。

3.2 螺栓数量和直径

改变连接螺栓的数量，其余设置保持不变，计算结果如表2所示。结果表明，随着螺栓数量的减小，螺栓最大轴拉载荷、最大弯矩载荷、最大等效轴拉载荷、最大Mises应力和舱段对接面的最大张口显著增大。螺栓最大轴拉载荷是理论计算结果的2.00～2.47倍，螺栓最大等效轴拉载荷是理论计算结果的3.44～4.26倍。随着螺栓数量的减小，螺栓轴拉载荷越接近理论结果。很明显，螺栓最大轴拉载荷与螺栓数量之间不是理论计算中的反比例关系。

改变连接螺栓的直径，其余设置保持不变，计算结果如表3所示。结果表明，随着螺栓直径的增大，螺栓最大轴拉载荷没有明显变化，螺栓最大弯矩载荷和最大等效轴拉载荷显著增大，最大Mises应力和舱段对接面的最大张口显著减小。螺栓最大轴拉载荷是理论计算结果的2.40～2.47倍，螺栓最大等效轴拉载荷是理论计算结果的4.26～7.06倍。虽然随着螺栓直径的增大，螺栓最大弯矩载荷和最大等效轴拉载荷显著增大，但螺栓有效承载面积和抗弯截面模量也随之显著增大，螺栓的最大Mises应力随之显著减小。

表2 不同螺栓数量对应的计算结果

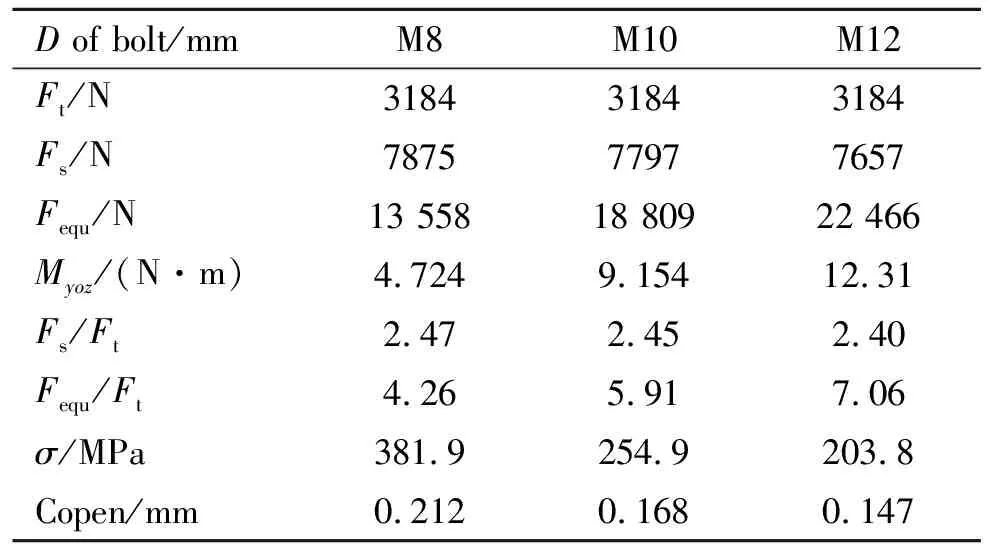
表3 不同螺栓直径对应的计算结果

3.3 螺栓分布圆直径

改变螺栓分布圆直径，其余设置保持不变，计算结果如表4所示。结果表明，随着螺栓分布圆直径的增大，螺栓最大轴拉载荷、最大弯矩载荷、最大等效轴拉载荷、最大Mises应力和舱段对接面的最大张口显著减小。螺栓最大轴拉载荷是理论计算结果的1.45～2.47倍，螺栓最大等效轴拉载荷是理论计算结果的2.43～4.26倍。随着螺栓分布圆直径的增大，螺栓轴拉载荷越接近理论结果。这是由于随着螺栓分布圆直径的增大，螺栓越靠近舱壁，“杠杆效应”中螺栓对应的力臂越接近舱壁的力臂，螺栓轴拉载荷的放大效应越不明显。

表4 不同螺栓分布圆直径对应结果

3.4 法兰厚度

改变舱段的法兰厚度，其余设置保持不变，计算结果如表5所示。结果表明，随着舱段法兰厚度的增大，螺栓最大轴拉载荷没有明显变化，螺栓最大弯矩载荷、最大等效轴拉载荷和最大Mises应力明显减小，舱段对接面的最大张口先减小，然后保持恒定。随着法兰厚度增加，舱段刚度增大，螺栓相对舱段法兰的刚度减小，螺栓最大弯矩载荷减小。

表5 不同法兰厚度对应计算结果

4 结论

使用有限元软件ABAQUS，对舱段连接结构进行了仿真分析，获得了舱段弯矩作用下的舱段连接螺栓组的轴拉载荷、弯矩载荷、螺栓应力和舱段对接面的张口，并与工程理论计算结果进行了对比分析。

进一步研究分析了螺栓预紧力、螺栓数量、螺栓直径、螺栓分布圆直径和法兰厚度对螺栓连接结构的影响。结果表明，在舱段弯矩载荷作用下：

(1)螺栓最大轴拉载荷的有限元计算结果是工程理论计算结果的1.45～2.53倍，在线弹性范围内，同时考虑螺栓轴拉载荷和弯矩载荷的螺栓最大等效轴拉载荷的有限元计算结果是工程理论计算结果的2.43～7.06倍；

(2)螺栓的弯矩载荷显著增大了螺栓的最大应力；

(3)螺栓的最大轴拉载荷随着螺栓数量的减少、螺栓分布圆直径的减小而远离舱段直径，且显著增大，而螺栓直径大小、法兰厚度对其影响较小；

(4)螺栓的最大弯矩载荷随着螺栓数量的减少、螺栓直径的增大、螺栓分布圆直径的减小而远离舱段直径、法兰厚度的减小而显著增大。