基于卷积神经网络的固体火箭发动机内弹道参数辨识①

孙瑞阳，姜 毅，牛钰森，张曼曼，强新伟

(1.北京理工大学 宇航学院，北京 100081；2.中国船舶集团公司713所，郑州 450015)

0 引言

考虑到经济、环保等因素，判断长期贮存的固体推进剂各项参数是否满足发动机使用要求具有重要意义。由于实验测量过程较为繁琐、资源消耗较大，常用数值模拟方法进行固体火箭发动机内弹道参数辨识。庄建华等基于拉丁超立方设计(LHD)的方法对内弹道模型中的燃速系数、压强指数及侵蚀燃烧模型参数进行辨识；郭风华等使用有限元软件进行仿真计算，同时与实验结果对比；魏瀚、范健等采用CAD实体造型法，通过访问几何造型平台内核来计算燃面-肉厚关系，带入内弹道验证计算；张小平、王晓锋等利用神经网络预示推进剂燃烧性能变化规律；樊超等基于遗传算法，利用固体火箭发动机燃速模型和喉径变化模型进行参数辨识；褚佑彪等用残值函数法模拟出了变燃速药柱的燃面推移过程，分析了高低燃速推进剂交界面的位置对药柱燃面演化过程和内弹道的影响。然而，针对长期贮存的固体推进剂，众多学者大都依靠数学公式或隐藏层较少的神经网络进行推导求解，这些方法的本质均是将压强随时间变化的离散数值点进行迭代，存在效率低、计算成本高、模型不易收敛、准确率低等缺陷。因此，依然需要一种适合工程应用、资源消耗小，同时准确率高的方法来求解固体推进剂重要参数。

根据现有内弹道参数辨识技术结合卷积神经网络，本文提出一种基于卷积神经网络的固体火箭推进剂参数辨识方法。首先，将燃速系数和压强指数带入固体火箭发动机内弹道程序中，根据变化参数的数量，对应生成若干张压强-时间曲线图像，以此作为卷积神经网络训练样本集；然后，通过卷积神经网络对样本集训练，获得卷积神经网络模型；最后，将此模型带入卷积神经网络辨识程序，获得内弹道燃速系数和压强指数，从而计算得到对应压强下的辨识燃速。该方法可以较为准确地获得燃速结果，不存在迭代算法中发散的问题，且误差控制在1%以内。

1 辨识模型

基于经典AlexNet网络，设计针对固体火箭发动机内弹道参数辨识卷积神经网络，本章节详细介绍完成该任务的辨识流程及采用的网络框架结构。

1.1 辨识流程

参数辨识流程如图1所示。

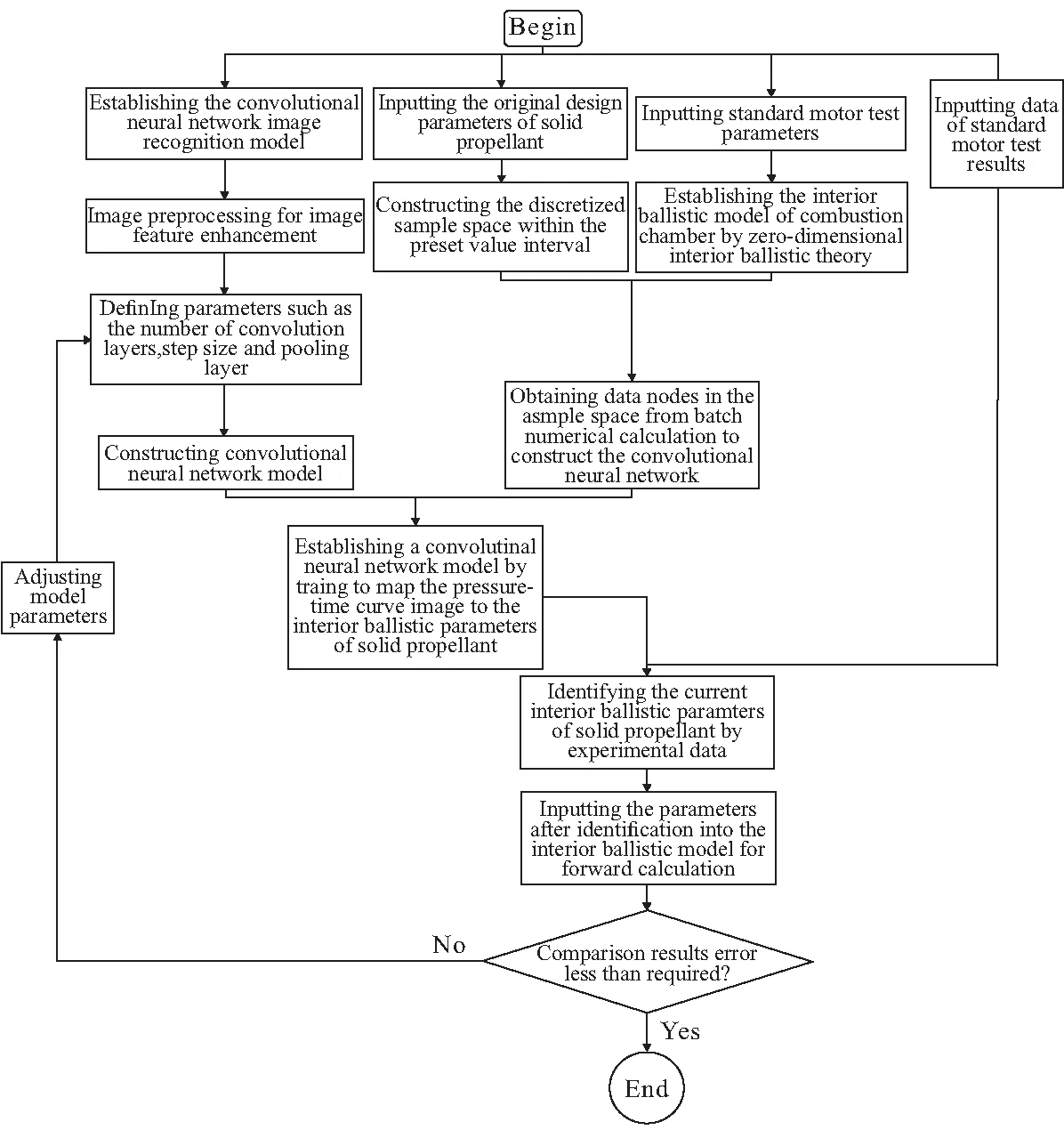
图1 内弹道参数辨识流程Fig.1 Identification process of internal ballistic parameters

主要流程：

(1)基于卷积神经网络中经典的AlexNet训练模型的连接层及参数，将推进剂的对应参数输入固体火箭发动机内弹道程序中，程序基于固体火箭发动机零维内弹道，其计算公式如下：

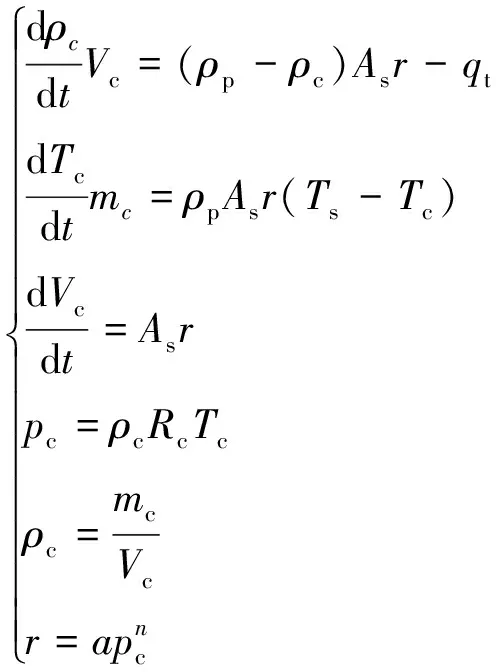
(1)

式中为燃气密度；为时间；为燃烧室容积；为推进剂密度；为燃面面积；为燃速；为喷管喉部的质量流量；为燃烧室内温度；为燃烧室内生成气体的总质量；为推进剂绝热燃烧温度；为燃烧室内压强；为气体常数；为燃速系数；为燃速压强指数。

通过计算得到的离散点集，判断该内弹道模型是否与实验内弹道模型一致。

(2)待模型校对一致后，通过改变固体火箭发动机内弹道的两参数——燃速系数和压强指数，生成若干组压强-时间的离散点集，并绘制曲线，生成图像集(生成的图像采用位图文件存储格式，其具体存储形式为每一个像素点存储3个8位十六进制数)。

(3)将图像集输入卷积神经网络中进行训练，生成卷积神经网络。

(4)将实验图像带入训练模型中，获得燃速系数和压强指数。

(5)根据辨识得到的燃速系数和压强指数值带入固体火箭发动机内弹道程序中进行正向计算，判断误差是否满足要求：若误差不满足要求，则根据图像特征修改卷积神经网络模型中的参数，再次进行神经网络的训练；若误差满足要求，则可确定卷积神经网络的参数，由此生成了有针对性的固体火箭发动机内弹道参数辨识卷积神经网络及训练模型。

1.2 卷积神经网络结构设计

1.2.1 输入层

整个网络的输入，一般代表了一张图片的像素矩阵。图2中最左侧三维矩阵代表一张输入的图片，三维矩阵的长、宽代表了图像的大小，而三维矩阵的深度代表了图像的色彩通道(channel)。在本模型中，输入层(input)是选定辨识参数后，通过内弹道计算得到的若干张内弹道压强-时间曲线图像(每张图像的燃速系数和压强指数不相同)，每张均为227×227像素、RGB 色彩模式，在该模式下图像的辨识深度为3。

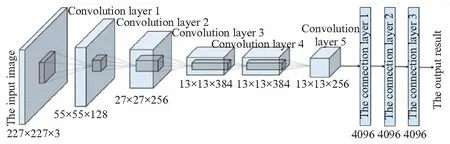
图2 AlexNet构架Fig.2 The AlexNet architecture

1.2.2 卷积层

卷积层(convolutional layer,Conv)是所有类型的卷积神经网络中最为重要的部分。与全连接层不同，这一层由可学习的过滤器组成。卷积层中每一个节点的输入只是上一层神经网络中的一小块，通过卷积层处理过的节点矩阵会变得更深。

卷积层中一个神经元的输出可以通过如下公式计算：

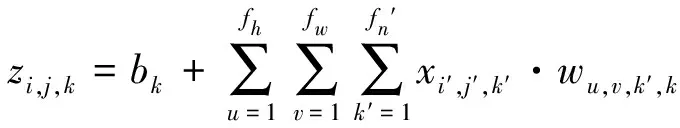
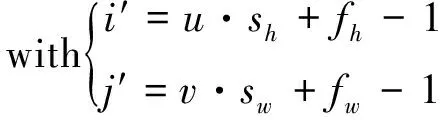
(2)

式中,,为当前卷积层第个特征图中行列的神经元的输出；和为垂直和水平步长；和为接收域的宽和高；′为前一层特征图的数目；′,′,′为下一层第′个特征图或通道中′行′列神经元的输出；为一层中第个特征图的偏移项，可以调整特征图的亮度；,,′,为一层第个特征图中任意一个与其输入层第′个特征图中位于行列的神经元(依赖于一层神经元的接收域)之间的连接权重。

1.2.3 归一化层

归一化层(batch normalization，BN)是对一个小批处理中的每个输入通道进行规范化。为了加快卷积神经网络的训练速度，降低对网络初始化的敏感性，主要在卷积层和非线性层之间使用。

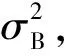
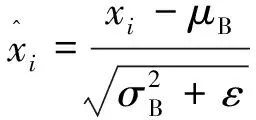
(3)

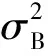
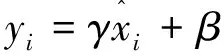
(4)

其中，偏移量和尺度因子是可学习的参数，在网络训练过程中不断更新。

1.2.4 激活函数

激活函数(ReLU)的作用是增加了神经网络各层之间的非线性关系。在本文辨识模型中，使用ReLU激活函数，其主要优势为：对于线性函数而言，ReLU的表达能力更强，尤其体现在深度网络中；而对于非线性函数而言，ReLU由于非负区间的梯度为常数，因此不存在梯度消失问题(Vanishing Gradient Problem)，使得模型的收敛速度维持在一个稳定状态。

ReLU层对输入的每个元素执行阈值操作，其中任何小于零的值都被设为零：

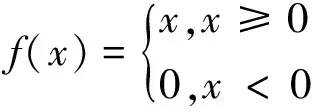
(5)

图3 ReLU函数作用示意图Fig.3 Diagram of ReLU function

1.2.5 池化层

池化层(maxpool layer)通常跟随在卷积层后，通过池化层，可以进一步缩小最后一个全连接层中节点的个数，从而到达减少整个神经网络参数的目的。

池化层可以非常有效地缩小矩阵的尺寸(主要减少矩阵的长和宽，一般不会去减少矩阵深度)，从而减少最后全连接层中的参数。使用池化层既可以加快计算速度，也可以有效防止过拟合问题。

1.2.6 全连接层

全连接层(fully connected layers，FC)是对前层是全连接的全连接层转化为卷积核为1×1的卷积，前层是卷积层的全连接层可以转化为卷积核为×的全局卷积，和分别为前层卷积结果的高和宽。在经典的卷积神经网络中，FC层的参数占总参数的绝大部分，因为全连接层的每一个结点都与上一层的所有结点相连，需要把前边提取到的特征综合起来。本次参数辨识需要获得输入图片对应的输出参数，因此最后一个全连接层仅需要2层参数，这大大减小了全连接层参数的数量，提高了整个神经网络训练效率。

1.2.7 防止过拟合层(dropout layer)

在全连接层训练过程中，由于全连接层的每一个结点都与上一层的所有结点相连，一方面会导致神经网络训练费时，另一方面也会使训练结果过拟合。为解决上述问题，在训练过程中用“Dropout”(弃权)方法改善过拟合情况，有效地避免了因训练样本不足而导致的网络过拟合现象。

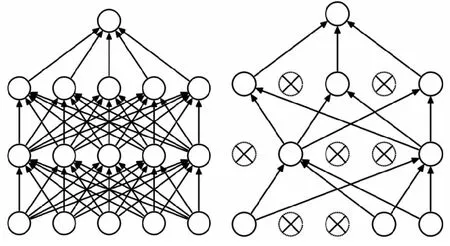
(a)Standard neural net (b)After applying dropout图4 Dropout层作用示意图Fig.4 Schematic of the Dropout layer

1.2.8 损失函数

为确定卷积神经网络模型性能，需设置损失函数进行评判。任何机器学习模型的目标都是通过训练使损失函数的值最小化，尤其是在预测模型更接近已知数据集的时候。该辨识模型所考虑的损失函数是如下所示的均方误差，这是典型的回归问题：

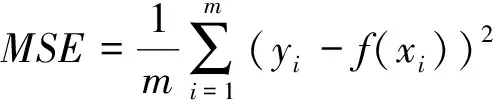
(6)

式中和()分别为第个样本的真实值和预测值；为样本个数。

本文使用的卷积神经网络模型共设置1000个迭代步，即损失函数对辨识模型进行1000次整体修正。

2 实验结果及分析

为检验AlexNet网络性能是否改进，结合实验结果，将压强-时间曲线图像通过改进AlexNet网络进行训练，并根据结果准确率进行分析。

2.1 数据集

通过建立的固体火箭发动机内弹道程序，设置不同的燃速系数和压强指数，得到若干张如图5所示的压强-时间曲线图像(该内弹道为测试单根药柱的燃烧性能而设计，故最大压强和最小压强差值较大)。燃速系数和压强指数取值范围根据推进剂出厂时提供的参数范围确定。

样本点的范围确定后，即明确燃速系数和压强指数的取值范围之后，需将燃速系数和压强指数值通过拉丁超立方随机采样的方法进行随机组合，从而确定生成图像的样本点。由于该样本区间较大，导致生成的压强-时间曲线图像的时间范围和压强范围较大，从而影响辨识结果精度。为解决该问题，在采样区间选择一定燃速范围内的样本点对应的燃速系数和压强指数生成压强-时间曲线图像，其采样结果如图6所示。

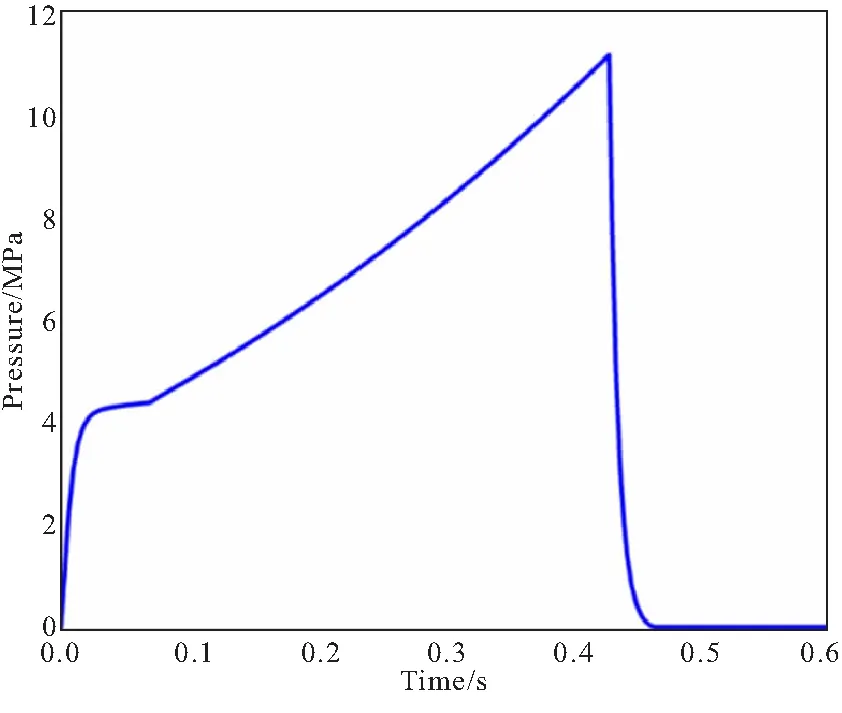
图5 压强-时间曲线Fig.5 Pressure-time curve graph

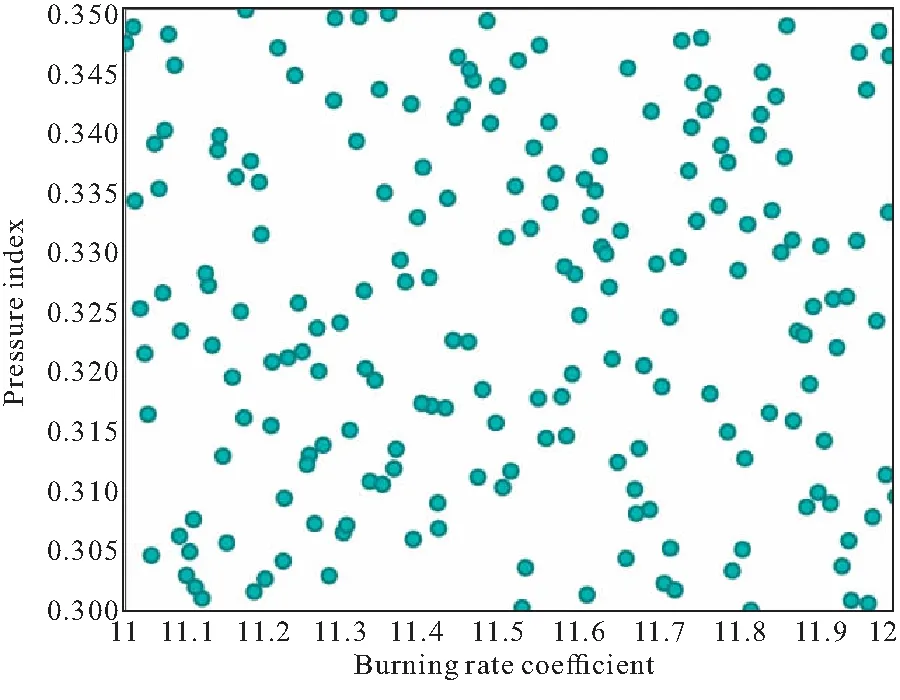
图6 拉丁超立方采样结果Fig.6 Latin hypercube sampling results

2.2 曲线处理

由于实际燃烧过程中初始阶段可能存在侵蚀燃烧，结尾段装药不均可能导致燃烧速率低于理论值等随机情况，均无法通过理论分析准确预估。为保证结果的准确性，决定选取稳定上升段的压强-时间曲线图像进行辨识，从而消除实验的压强-时间曲线图像中上升段和拖尾段的图像与理论不符从而影响运算误差的情况。在本实验中，选取0.1～0.4 s，4～11 MPa的图像生成样本集，如图7所示。

2.3 图像增强

在卷积神经网络训练之前，需要对生成的曲线进行图像增强，以获得神经网络可识别明显特征的图像信息。本实验中，对图像进行随机旋转和随机平移，有目的地强调图像的整体或局部特性，将原来不清晰的图像变得清晰或强调某些感兴趣的特征，扩大图像中不同物体特征间的差别，抑制不感兴趣的特征，从而改善图像质量、丰富信息量，加强图像判读和识别效果。

计算模型所设置的参数为图像随机旋转-20°～20°之间，沿轴及轴方向均随机平移0～6像素。图像增强处理后，输出图像的尺寸依然设置为227×227，与输入尺寸一致。

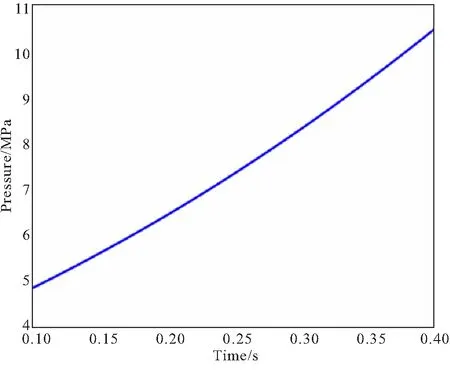
图7 卷积神经网络训练样本集图像Fig.7 Training sample set image of convolutional neural network

2.4 卷积神经网络训练

卷积神经网络以一种可扩展的方式从复杂的真实数据中捕捉不变性，这是由于其具有局部接受域子结构，该结构具有权值共享并随后通过子采样层进行映射的能力。AlexNet是在经典卷积神经网络LeNet5和传统BP神经网络基础上进一步发展和改进的深度卷积神经网络。其中，使用的ReLU激活函数加快了网络的收敛速度，并且有效防止梯度消失等问题；在全连接层使用“Dropout”技术，避免了过拟合现象；在第二卷积层和第三卷积层之前，对输入数据进行LRN操作，避免了网络模型参数在训练过程中不断更新导致每个后续层的输入数据分布发生变化。

本模型基于AlexNet搭建连接层并确定其相关参数，网络框架图与参数设置如图8所示。在模型训练过程中运用数据增强、随机失活、ReLU激活函数和局部响应规范化(LRP)的训练技巧，使用了5个卷积层、3个池化层和3个全连接层对图片参数进行处理。

表1显示了经典AlexNet不同层的特征尺寸和参数数量，总参数量为6096多万。本文所提出的辨识模型参数设置如表2所示，其中共需要参数总量为5605多万，是经典AlexNet总参数的91.95%。

表1中网络参数量的计算公式为

=××

(7)

式中为卷积核的大小；为卷积核通道数；为输出特征图的通道数。

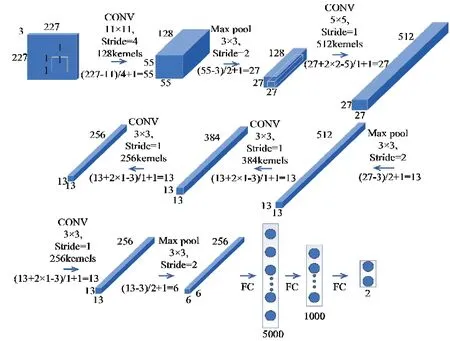
图8 内弹道参数辨识卷积神经网络框架Fig.8 Convolutional neural network framework for internal ballistic parameters identification

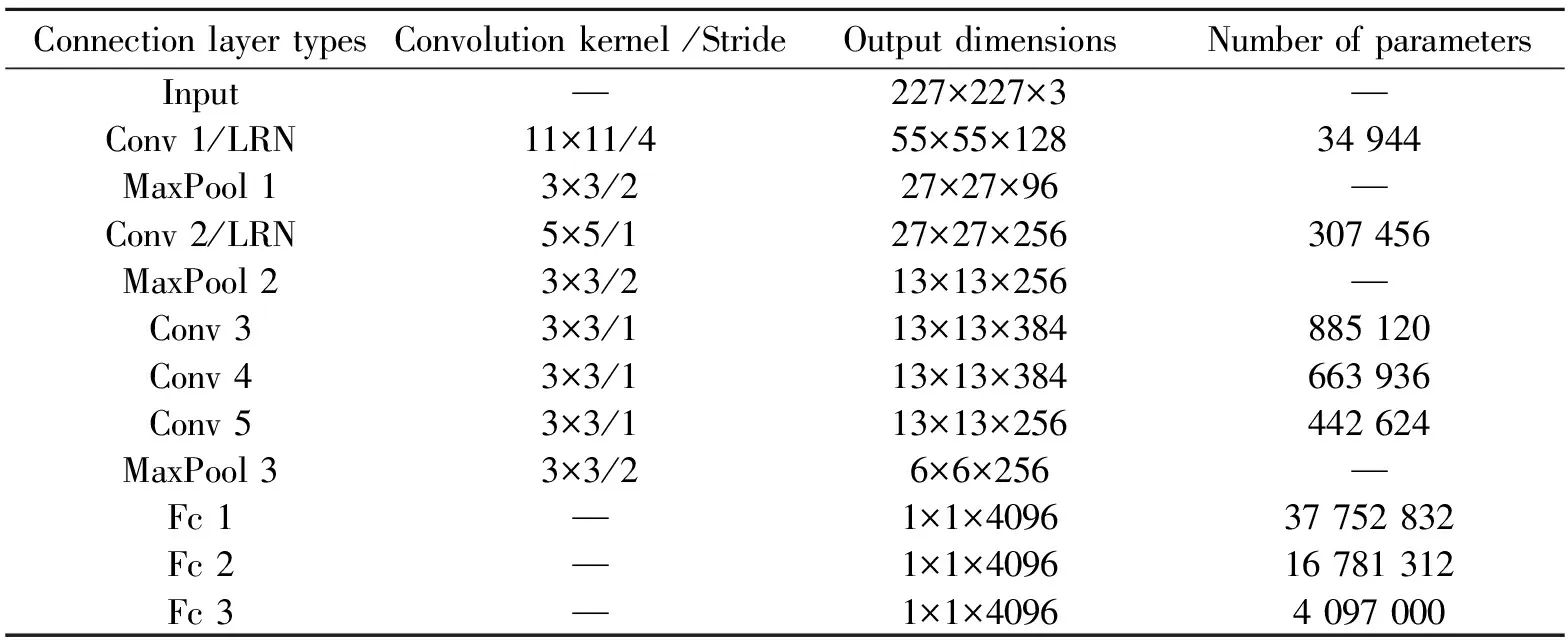
表1 AlexNet网络参数设置

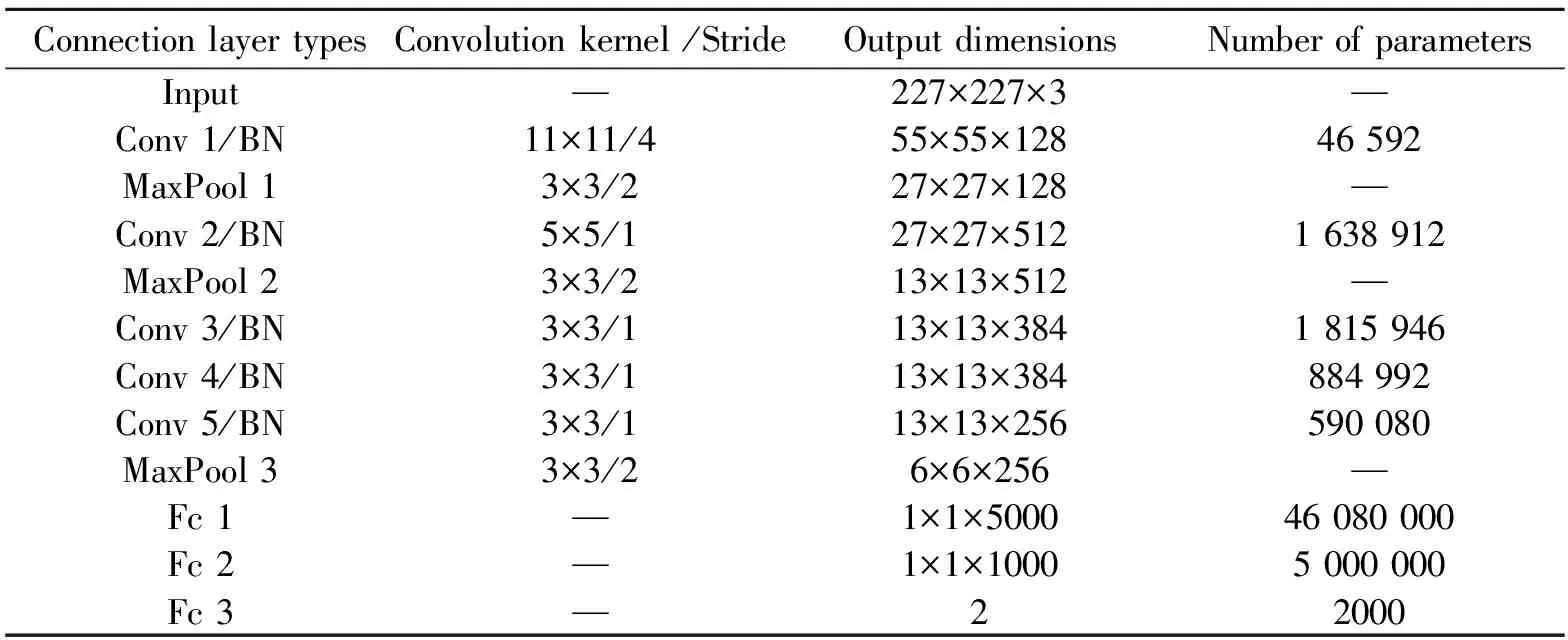
表2 辨识模型网络参数设置

从表1可见，网络的参数主要集中在全连接层，其中全连接层的参数占总参数的96.17%，容易造成过拟合现象，这是由于传统的AlexNet算法大都进行图像识别，因此第三层全连接层的输出参数较大，其目的是为保证图像辨识结果的判断参数足够大，从而保证结果的准确性。而该辨识模型需要解决的参数回归问题，最终需要将图像与参数匹配的结果作为训练结果，且压强-时间曲线所生成的图像所含特征较少，参数过多容易导致过拟合。因此，如表2所示，计算模型所使用的网络中全连接层参数为5108.2万个，占总参数的91.12%，相比于经典AlexNet，全连接层参数总量减少了5.05%，从而更好地解决网络的过拟合现象。

2.5 实验设计及结果

该辨识任务的主要难度在于图像特征少于普通图像，导致结果易出现过拟合问题，且曲线图像中包含的特征与普通情况的图片识别相比特征值少，相比于普通的图像识别问题，参数辨识问题要求的辨识精度更高。对于该情况，选定高精度参数值是很重要的。表3所示为设定不同数据集样本量、训练集数据占比及验证集数据占比，获得训练所得的燃速系数辨识准确率及压强指数辨识准确率。

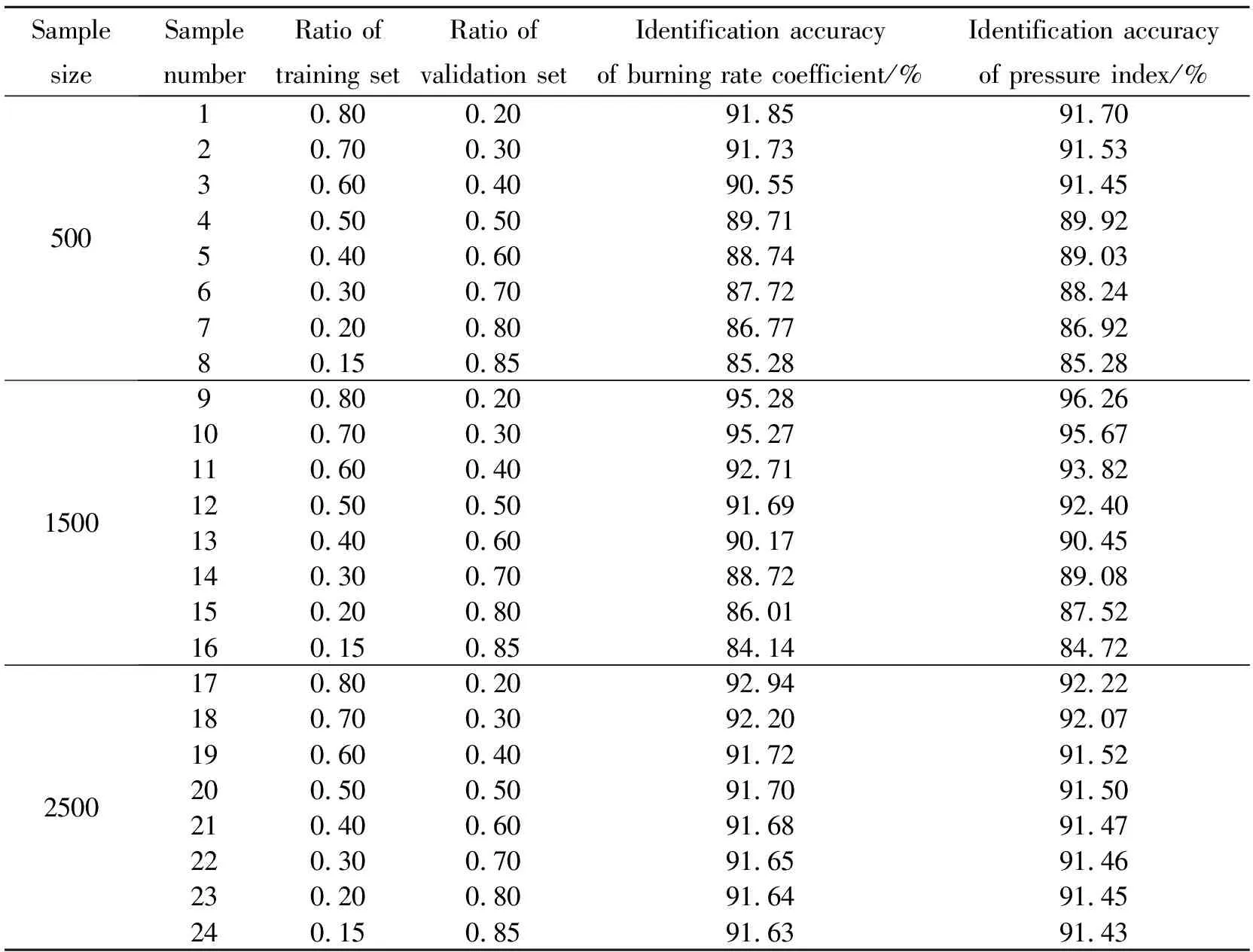
表3 卷积神经网络训练结果

2.6 结果分析

根据表3中结果，得到相同数量样本集、不同比例训练集的燃速系数和压强指数辨识准确率结果，如图9所示。根据卷积神经网络结果准确率对比图中可以得出以下结论：

(1)当训练集占比为15%时，准确率最小，样本集为500张和1500张时准确率均为85%左右，样本集为2500张时，准确率超过了90%，随着训练集占比数量增大，准确率持续增长，当训练集占比为80%时，样本集为500张和2500张时，准确率均为92%左右，样本集为1500张时，准确率为96%左右。

(2)当训练集占比数量相同时，样本集数量为500和2500时，其准确率均小于样本集为1500时，这表明样本集数量为当训练集数量为500张时，图像样本集数量可继续增加，使卷积神经网络学习更多特征，当样本集数量达到2500张时，已经出现了过拟合的趋势；

(3)当样本集数量一定时，训练集比值越大，训练的准确率越高，但这种情况也有可能是由于测试集数量减少导致的准确率提高，有可能使训练得到的神经网络普适性较低。

训练结束后，将待辨识的实验压强-时间曲线图像放入训练卷积神经网络得到的训练模型中，图像如图10所示。为保证坐标系不干扰重要特征的提取，将实验曲线的图像设置其横纵坐标与理论内弹道生成的压强-时间曲线图像一致。得到实验曲线图像的燃速系数和压强指数的辨识结果，将结果带入内弹道后，将实验结果与理论结果进行对比，其结果如图11所示。由实验数据可以看出，0.127～0.413 s为上升工作段，在该段实验值与理论值数据集误差最大值为0.203 MPa，平均误差值为0.101 MPa，是峰值误差的0.9%。为验证辨识结果的准确性，根据实验测试，截取药柱进行返厂燃速测试，测得在20 ℃、9.81 MPa下的燃速为22.5 mm/s，根据辨识结果，药柱燃速为22.28 mm/s，与测得的实验结果比，其误差为0.98%。

由推进剂出厂数据显示知，在20 ℃、9.81 MPa下推进剂的燃速为22.6 mm/s，贮存15 a后，其燃速下降了1%，但依然满足该推进剂出厂时规定的使用要求。其中，推进剂燃速下降与推进剂贮存环境以及自身材料特性有关。

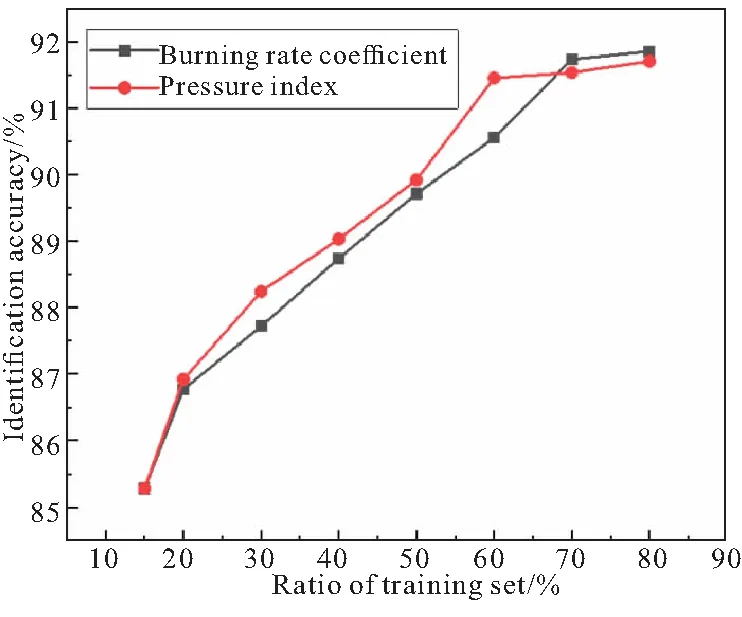
(a)The sample size of 500

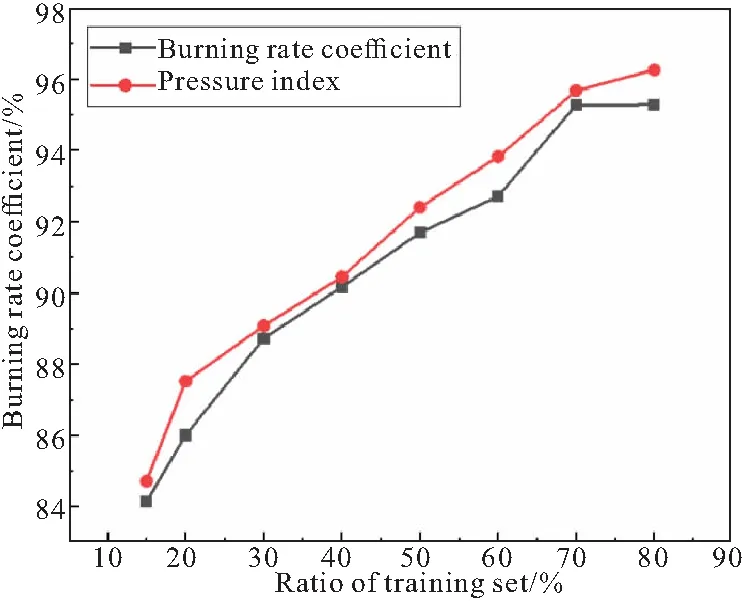
(b)The sample size of 1500

(c)The sample size of 2500图9 卷积神经网络结果准确率对比Fig.9 Accuracy comparison of convolution neural network result

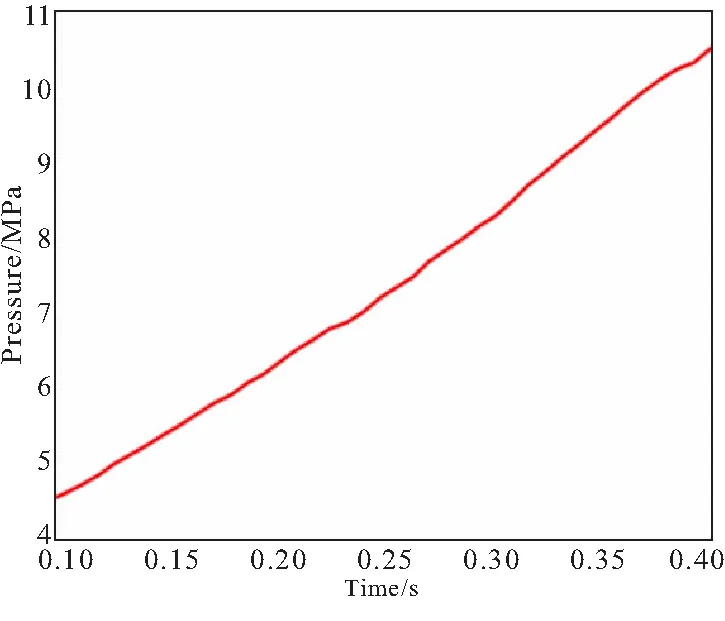
图10 实验压强-时间曲线截取图像Fig.10 Part of the experimental pressure-time curve image

图11 实验结果与辨识结果对比图像Fig.11 Image of the experimental result comparing with the identification result

3 结论

本文提出了一种基于卷积神经网络的固体火箭发动机内弹道参数辨识方法，此方法基于经典AlexNet网络模型，将固体火箭发动机内弹道的燃速系数和压强指数两重要参数通过理论压强-时间曲线建立样本集，训练卷积神经网络模型后，辨识实验压强-时间曲线图像中的燃速系数和压强指数值，其结果与实验值的误差在可接受范围内。

该辨识模型的研究价值主要基于以下三点：

(1)针对性地对AlexNet网络设计，与经典AlexNet方法相比，本文提出的方法针对参数辨识主要有两点优势：一是设计一种特殊的卷积神经网络用于内弹道参数辨识任务，即更改相关参数，尤其是全连接层的参数，在减小计算量的同时使卷积神经网络在完成参数识别任务时达到最佳准确率；二是使用BN层代替经典网络中的LRN层，加快了网络的收敛速度，并在一定程度上防止了过拟合现象。

(2)对于长期贮存的固体推进剂的参数辨识，可节省成本。本实验中所建立的辨识数据集是针对理论内弹道，修改其燃速系数和压强指数获得的压强-时间参数值来进行样本集的训练，此过程不需要大量的实验数据和结果，只需要若干验证数据集，因此可节省大量的时间和经济成本。

(3)根据相关内弹道模型可以设置多个变量进行参数辨识。在实验过程中，基于燃速系数和压强指数两个变化参数，增加喷管喉部直径这一变化参数后，计算求解时间和资源成本几乎没有增加，即内弹道变化参数增多，更能凸显使用卷积神经网络的优越性。本文所使用的内弹道模型忽略了发动机侵蚀燃烧现象，使实验结果与辨识结果在0.1 s附近产生一定误差偏离；截取燃烧稳态段(0.1～0.4 s)进行卷积神经网络辨识，这可能会导致辨识精度降低。因此，在后续的研究工作中，将针对上述不足进行完善，从而提高模型的辨识准确度。