实测燃速处理误差对内弹道性能预示的影响分析①
刘 杨,丁 淼,白彦军,李卓然
(中国航天科技集团有限公司四院四十一所 燃烧、热结构和内流场重点实验室,西安 710025)
0 引言
固体火箭发动机的内弹道主要指发动机在设计或非设计状态下燃烧室及喷管内流动参数随时间或空间的变化规律,根据简化程度的不同,分为零维内弹道、一维内弹道和多维内弹道。零维内弹道将发动机内部参数看作平均值,主要解决燃烧室平均压强随时间的变化规律,零维内弹道计算方法简单、直观,在适当修正的基础上能够得到比较满意的计算结果,是工程上实用的求解方法。固体火箭发动机的内弹道对发动机性能有重要影响,能够决定飞行器能否按照规定的推力-时间历程工作。因此,内弹道性能预示精度是导弹系统最重要的指标之一,是影响全弹射程、精度等指标的关键因素。
为提高全弹的性能水平,弹总体往往对发动机内弹道性能预示精度提出较高的要求。内弹道性能预示方法最著名的是美国NASA的SPP方法,国内工程上有各种预示方法,主要利用零维平衡压强公式为基础采用多台实测结果反算燃面并加以修正,进一步计算试验或交付发动机的压强、推力和流量曲线。为提高内弹道性能预示精度,窦毅芳等通过对内弹道计算模型进行优化,提出采用基于径向基函数的响应面法建模,可以提高内弹道拟合精度和计算效率。邹汝平等通过建立固体发动机一维混合内弹道计算模型,提出了提高内弹道性能预估精度的工程方法,并对内弹道计算不确定性进行了研究。李春艳等对现有固体发动机内弹道性能计算方法进行适应性修改,建立了适用于短时间工作固体发动机的高精度内弹道计算方法。
发动机内弹道预示误差是综合因素作用的结果,包括传感器误差、测量误差、环境误差、计算误差和随机性误差等。在工程中,发动机内弹道性能预示往往从既有的试车数据着手,对试车数据进行分析、计算得到发动机反算燃面等数据;然后,根据燃速表征发动机燃速和燃速相关性计算得到的全尺寸发动机燃速(工程上对全尺寸发动机和燃速表征发动机之间燃速相关性的描述常用差值关系);最后,结合反算燃面数据和燃速进行单发发动机的内弹道性能预示。本文从当前工程对实测数据的处理方法入手,通过理论分析和不同压强比发动机实测数据,研究当前数据处理方法对发动机内弹道性能预示精度的影响,同时根据分析结果,提出发动机实测数据的修正计算方法。
1 从实测数据出发预示内弹道的方法分析
1.1 工程中实测数据的处理方法
当前发动机内弹道性能预示流程如图1所示。

图1 发动机内弹道性能预示的流程Fig.1 Performance prediction of SRM internal ballistic
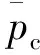

(1)
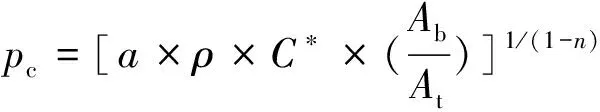
(2)
式中为时间所对应的发动机压强;为压强指数;为推进剂密度;为特征速度;为燃面面积;为喉面面积。
1.2 计算方法带来的误差分析
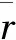
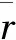
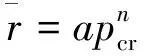
(3)
而
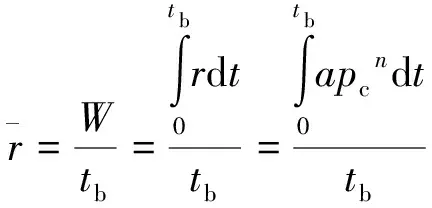
(4)
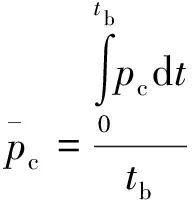
(5)
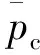
假设:
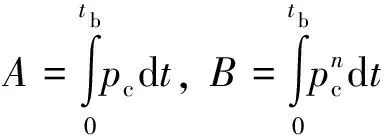
(6)
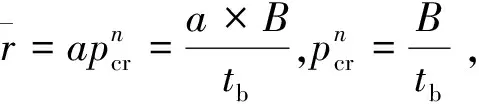

(7)

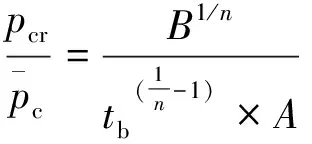
(8)


1.2.1 燃速误差分析
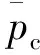
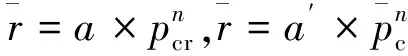

(9)
与之间的相对误差为

(10)
即反算燃速与实际燃速之间相对误差。
1.2.2 反算燃面误差分析
将燃速系数′、分别代入燃面-压强公式:

(11)

(12)
其中,、、、均为实测数据。则有

(13)
与之间的相对误差为
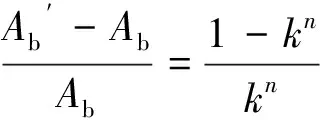
(14)
1.2.3 由反算燃面预示压强的误差分析
考虑由、计算压强、带来的误差。假设预示发动机的燃速已知,则
为提前精准锁定即将发生异动事件,甚至是停运故障的配变设备,为运维人员主动运维、提前安排抢修工作赢得宝贵时间,有效防范配网异动风险,本文通过构建配变重过载、低电压等异常状态预警模型,能够提前7天预测即将配变异常状态的精准预测,可精确到96个时刻点。
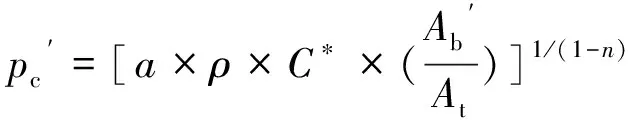
(15)
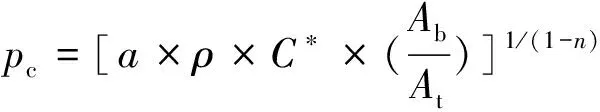
(16)

(17)
与之间的相对误差为

(18)
1.3 实测数据的修正计算方法

1.4 实验算例对比分析
根据以上分析结果,计算了不同压强比(压强比为1.1~1.3)发动机根据实测数据采用两种燃速处理方式带来的反算燃面的误差对比,如图2所示。
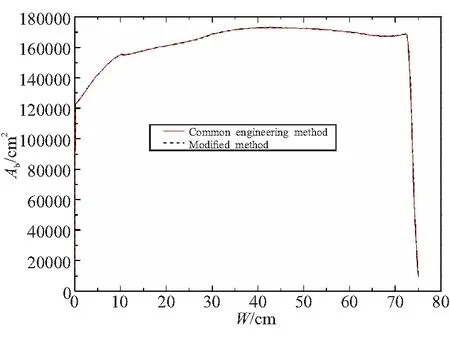
(a)Pressure ratio is 1.1
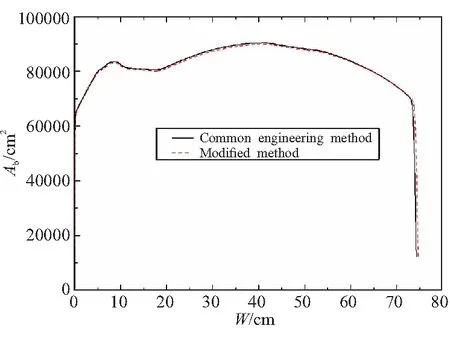
(b)Pressure ratio is 1.2

(c)Pressure ratio is 1.3图2 不同压强比的发动机燃面计算误差Fig.2 Calculation error of SRM combustion surface at different pressure ratio
由图2可以看出,发动机压强比大,两种计算方法计算得到燃面的相对误差也就大。发动机压强比为1.1时,两种方法计算的燃面相对误差约为0.1%~0.5% (不同压强指数带来的相对误差不同);当发动机压强比为1.2时,燃面的相对误差约为0.5%~1%;当发动机压强比为1.3时,燃面的相对误差约为1.5%~2.5%。
1.5 内弹道性能预示结果与遥测数据对比分析
前文提出了对实测数据的修正计算方法,为验证两种计算方法对内弹道性能预示精度的影响,本文根据某固体发动机地试的实测数据,通过两种不同的压强积分方法对燃面进行反算,从而得到燃面、燃速和燃速相关性等数据,其中两种方法反算的燃面结果如图3所示。
根据两种反算的燃面数据和该型飞行发动机的预示燃速(通过燃速表征发动机的实测燃速和燃速相关性计算得到)对其内弹道进行预示,预示结果与该发动机实际遥测数据进行对比,结果如图4所示。可明显看出,修正后的计算方法内弹道预示精度更高。其中,修正后方法预示平均压强的误差为1.5%,而传统工程方法预示平均压强的误差为2.3%。

图3 两种方法计算得到的燃面对比Fig.3 The comparison of SRM combustion surface calculated by the two methods

图4 内弹道性能预示结果对比Fig.4 The comparison of internal ballistic property prediction results
2 发动机内弹道性能预示精度分析
2.1 工程燃速相关性处理误差分析
当燃速相关性为差值关系时,假设燃速表征发动机燃速为,全尺寸发动机实测燃速准确值为,用近似处理方法得到全尺寸发动机燃速为。如果全尺寸发动机与表征燃速之间相关性为差值关系,则表示为
=+Δ,=+Δ
(19)

(20)
用两种方法计算发动机的压强为
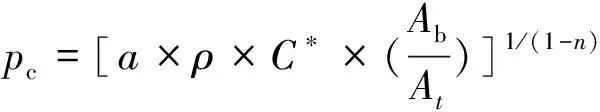
(21)

(22)
忽略喉径变化的影响,有

(23)
显然,当表征燃速稳定时:

(24)
两种方法得到的结果一致。实际中,燃速表征发动机燃速有一定波动,假设其波动系数为,则燃速表征发动机燃速为,两种方法计算的发动机压强之比为

(25)

2.2 改进燃速相关性处理方法分析
通过前文分析可以看出,若不采用本文提出的实测数据处理方法计算燃速系数,那么采用差值关系燃速相关性预示的压强将不可避免地产生计算误差。为了减小计算误差,可采用倍数关系描述燃速相关性。
当燃速相关性为倍数关系时,有=,=。于是,两种方法预示的发动机压强之比为
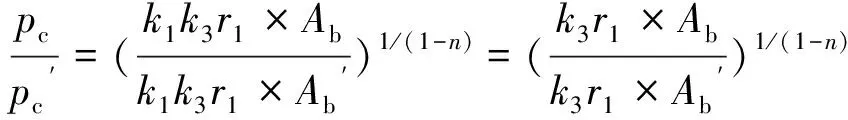

(26)
因此,燃速相关性为倍数关系时,近似处理方法可以减小预示结果的计算误差。
3 结论
(1)当前工程实测数据处理方法会带来反算燃面计算误差,不同压强比发动机数据处理带来的误差一般不同,通常压强比越大,误差越大。
(2)揭示了当前发动机数据处理方法误差产生的原因,从理论上提出修正的数据处理方法,并通过与遥测数据对比,表明修正后的方法内弹道性能预示精度更高,可为后续发动机内弹道性能预示提供指导。
(3)后续将进一步通过物理机理研究和更多型号发动机实测结果的大数据分析,对发动机内弹道性能预示方法进行评估和修正,进一步提高发动机内弹道性能预示精度。
- 固体火箭技术的其它文章
- 吸气式高速飞行器内外流耦合设计与多学科设计优化
- 固体发动机挂机滑块与壳体连接结构优化①
- 基于卷积神经网络的固体火箭发动机内弹道参数辨识①
- A novel energetic potassium salt of 2,3,5,6-tetranitro-4H,9H-dipyrazolo [1,5-a:5',1'-d][1,3,5]triazinane:Synthesis,crystal structure and performance①
- Formulation research on UV-curable polyether modified HTPB solid propellant for 3D printing①
- 缠绕工艺关键参数对T800碳纤维复合材料壳体强度的影响①

