多工况下变推力固体发动机喉栓喷管型面一体化优化设计①

王鹏宇，王政涛，武泽平，张 锡，张为华

(国防科技大学 空天科学学院，长沙 410073)

0 引言

固体火箭发动机具有结构简单、维护方便、可靠性高、可长期处于战备状态等优点，目前已在各类战术、战略导弹中得到广泛应用。传统固体火箭发动机缺乏节流措施，需要通过对装药构型进行详细设计以满足特定推力方案。喉栓式变推力发动机不仅保留了传统固体发动机的诸多优点，而且推力调节具有主动性、实时性、可大范围无极调节等优点，可提高固体火箭发动机性能，增强导弹机动性和突防能力，大幅提升导弹射程，已发展成为固体火箭发动机推力调节的重要研究方向。但是，喉栓运动改变喷管喉部面积实现推力调控的同时，不可避免地会影响喷管内燃气的流动情况，造成流动损失，甚至出现流动分离现象。BURROUGHS等对不同形状喉栓的变推力发动机进行试验和数值分析，发现在喉栓位置下游存在微弱激波。OSTRANDER等通过仿真分析喉栓介入对发动机流场的影响，结果表明，当喉栓沿轴线运动时，燃气流动方向偏离发动机轴线，造成一定的推力损失，且在喉栓头部及喷管扩张段内会出现流动分离现象，加重该区域内的烧蚀现象。因此，需要对喷管型面及喉栓型面进行整体优化，以减小喉栓介入所引起的流动损失。成沉等基于响应面法对喉栓式变推力发动机进行一体化优化设计，使得喉栓完全介入状态下比冲损失最小。由于变推力发动机实际工作过程中喉栓需在一定范围内移动，仅针对喉栓某特定位置进行型面优化无法综合考量发动机的性能。因此，变推力发动机优化过程需喉栓不同位置的进行多工况仿真计算。

本文基于Fluent进行喉栓式喷管多工况流场仿真计算，通过对喷管型面及喉栓型面控制参数进行优化设计，以期实现喉栓式喷管性能的提升。由于CFD模型求解耗时，直接进行数值优化设计计算成本难以接受。因此，本文采用基于代理模型的优化框架，实现型面控制参数快速优化，以满足工程优化设计效率需求。

1 优化设计模型

1.1 型面参数化

本文优化的喷管收敛段、喉部半径保持不变，而扩张段采用圆弧及三次曲线描述，设计变量包括扩张段过渡圆弧半径、扩张段过渡圆弧角、喷管出口倾角、喷管扩张段长度以及喷管扩张比。其中，喷管扩张比由式(1)给出：

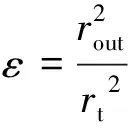
(1)

式中为喷管出口半径；为喷管喉部半径。

为保证喉栓运动过程中所形成的等效喉部面积最大、最小值相同，喉栓半径保持不变，而喉栓头部型面则采用双圆弧切线构型，由喉栓头部长度、喉栓头体过渡圆弧半径以及喉栓头部圆弧半径等设计变量唯一确定，喷管和喉栓构型示意如图1所示。

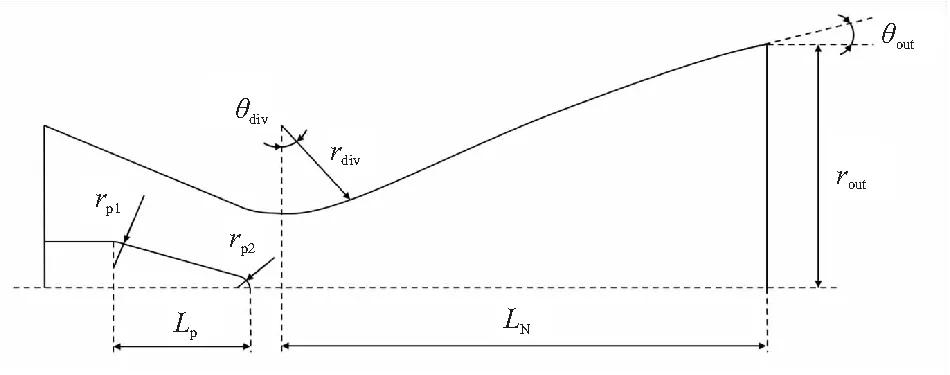
图1 喷管及喉栓型面示意图Fig.1 The contour of the pintle nozzle

1.2 数值计算模型

本文采用Favre平均N-S方程，其在雷诺平均N-S (RANS)方程组的基础上提出密度加权平均概念，即压强和密度采用时间平均，其他变量采用密度加权平均。FANS方程组解决了RANS方程组处理可压缩流动较为复杂的问题，通适于不可压缩流动与可压缩流动。

二维轴对称的FANS方程组的表达式为

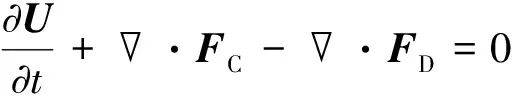
(2)

式中为流场守恒变量矢量；为对流通量矢量；为粘性扩散通量矢量。

其中，散度的表达式为

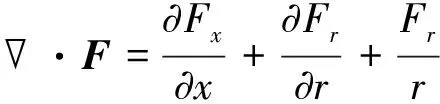
(3)

Favre平均N-S方程组中包含湍流粘性系数与湍动能，需通过求解湍流模型得到。本文采用Realizable-湍流模型，通过偏微分方程处理湍动能及其耗散速度。

边界条件是流场仿真计算的关键因素，本文设置入口边界条件为压力入口，不同于普通固体火箭发动机的定值压力入口，喉栓式变推力发动机喉栓运动过程中会引起燃烧室压力变化。因此，边界入口压强随喉栓的运动发生变化：

(4)

式中为推进剂密度；为特征速度；为燃速系数；为燃面面积；为等效喉部面积；为压强指数。

出口边界定义为压力出口，分别设定环境压强及环境温度；喷管、喉栓等壁面采用增强壁面方式处理。

由于喷管及喉栓型面变化较为复杂，本文采用非结构网格进行网格划分，并对壁面处进行适当加密处理，如图2所示。网格质量检测显示，所划分网格正交性良好，满足计算要求。网格尺度划分验证结果如表1所示。可以看出，当网格数量大于60 000时，流场结构变化较小。因此，选取60 000网格进行计算。

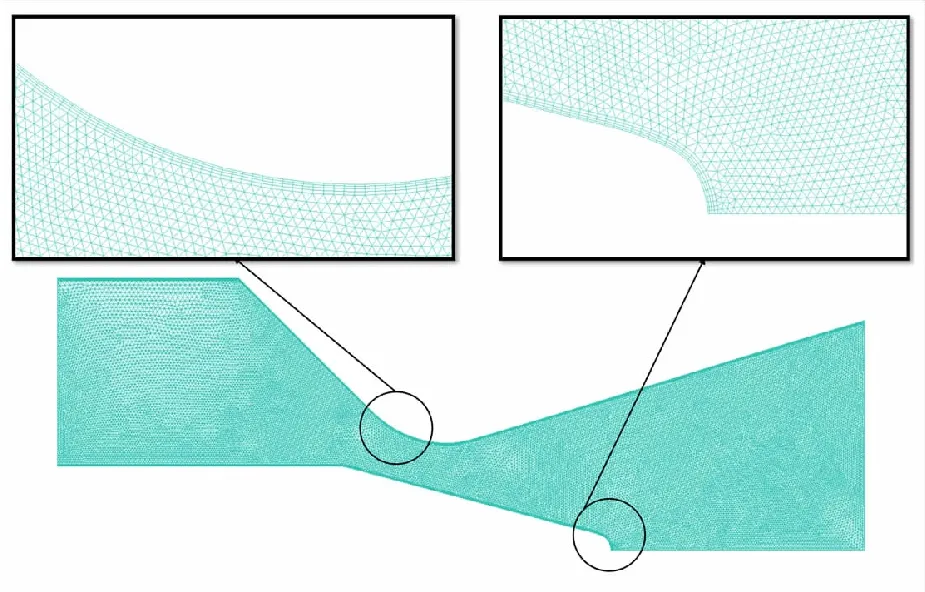
图2 计算域网格划分Fig.2 The grid of calculation domain

表1 网格无关性验证

2 基于代理模型的优化方法

基于代理模型的优化方法在20世纪80年代被首次提出，并成功应用于计算耗时的复杂模型优化问题。该方法基于少量的高精度采样点建立近似模型，用以在优化过程中替代复杂的高精度学科模型，通过对近似模型的搜索确定新的采样点并不断重构更新近似模型，以期逐渐逼近真实学科模型，预测全局最优解。基于代理模型的优化可以大幅减少真实模型的调用次数，从而提高优化设计效率，降低设计成本。

其主要步骤包括实验设计采样、构造代理模型以及序列近似采样等。基于代理模型的喉栓式变推力发动机型面优化流程如图3所示。

2.1 试验设计

实验设计是基于代理模型优化方法的关键步骤，直接影响着初始代理模型的质量，合理的实验设计方法可以获得更优的采样方案，以得到更多的空间信息。本文采用优化拉丁超立方实验设计方法，在设计空间内生成均匀的初始样本点。

2.2 Kriging模型

代理模型基于已有的样本点，采用简单的数学函数来对计算耗时的高精度仿真模型进行逼近，从而实现快速地对全设计空间函数值进行预测。龙腾等将目前使用较为广泛的多项式响应面模型、径向基函数模型、Kriging模型以及人工神经网络进行综合分析比较，发现Kriging模型在近似精度、鲁棒性等方面有着更好的综合性能。因此，采用Kriging模型对CFD真实模型进行逼近。

Kriging模型是一种基于随机过程的最优线性无偏估计。该模型通过高斯随机过程描述未知函数，并通过已知样本点对未知函数的响应进行预测，即

(5)

其中，为未知常数，表征变量域的整体变化趋势；()为局部随机偏差项，其均值为零，方差为。因此，设计空间内两点、的协方差可表示为

[(),()]=(,)

(6)

基于无偏性以及预测方差最小准则，可求得模型预测函数为

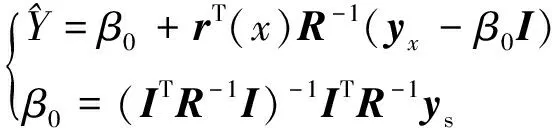
(7)

式中∈为个样本点响应值组成的维列向量；()∈为预测点与样本点的协方差；∈×为样本点协方差矩阵；∈为单位列向量。

此外，Kriging模型还能够给出预测方差：

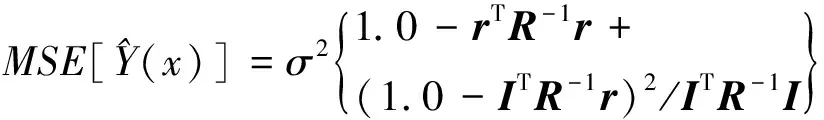
(8)

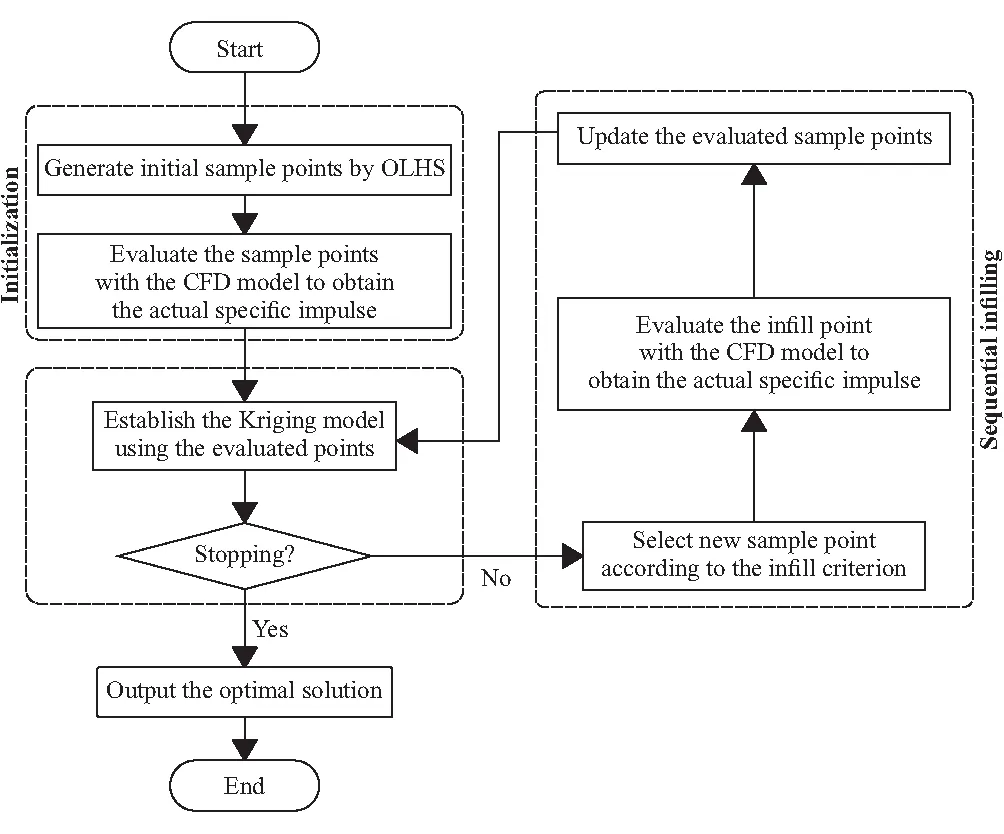
图3 型面优化流程图Fig.3 Optimization design flow chart for the contour

2.3 优化算法及序列采样准则

在基于代理模型的优化过程中，优化算法以特定采样准则为目标函数，在代理模型上搜索最优解作为新的样本点用以更新近似模型，称为“辅助优化”过程。本文在“辅助优化”过程中采用增强精英保留的多种群协同遗传算法，通过为不同的种群设置不同的交叉和变异概率丰富总群个体，并基于概率进行中群间的迁移，实现高效的全局收敛。

序列采样准则是基于代理模型优化过程的关键步骤之一，它直接影响着优化效率和结果的准确性。目前，工程实际中常用的采样准则为开发准则，即将代理模型的全局最优点作为新样本点来更新近似模型。开发准则忽略近似模型的全局精度，旨在最有潜力的区域进行采样，以加快算法的收敛速度。但由于样本量较少，代理模型在优化初期通常精度较低，对不精确的代理模型进行过渡的搜索会导致计算资源浪费，甚至可能将搜索进程引向前景较差的区域，陷入局部最优。

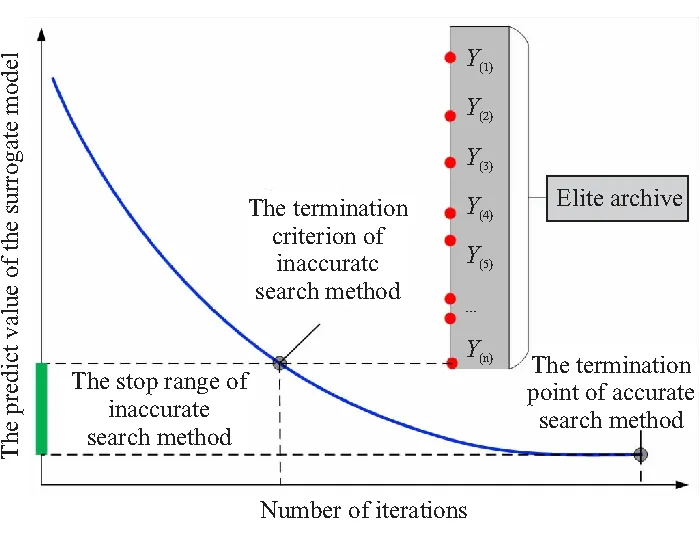
图4 基于不精确搜索的采样过程示意图Fig.4 Schematic diagram of sampling process based on inaccurate search

针对上述问题，学者将非精确搜索算法及外部精英库引入“辅助优化”过程，采用精英库动态存储所有精英个体，当发现比精英库最优解更为优秀的个体时，“辅助优化”过程立即停止，并采用高精度仿真模型计算该点的响应值。

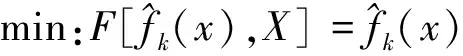
(9)

其停止准则为

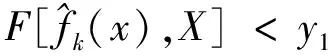
(10)

非精确搜索能够逐步地引导搜索过程朝着好的方向发展，可以有效陷入局部最优。因此，本文基于非精确搜索的开发准则序列填充新的样本点。

3 优化算例及结果分析

本文对已有喉栓式变推力发动机型面进行优化设计，基准构型设计变量及其上下限如表2所示。为衡量喉喉栓式喷管多工况条件下的实际性能，基于Fluent分别计算喉栓未介入状态(下称工况1)、喉栓部分介入状态(指等效喉部面积减小50%，下称工况2)以及喉栓完全介入状态(下称工况3)下喷管的实际比冲，并依据其工作时间进行加权平均，以此平均实际比冲作为衡量喷管性能的指标，即

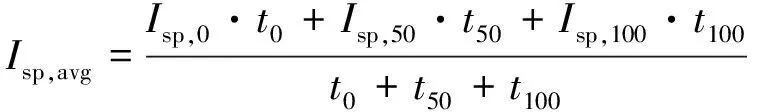
(11)

式中、分别为喉栓未介入状态及完全介入状态下的实际比冲；、分别为两种状态下的工作时间；为喉栓部分介入状态下的实际比冲；为该状态下的工作时间。

采用优化拉丁超立方实验设计方法生成20个均匀分布的初始样本点，对其进行CFD仿真计算后构建Kriging模型。基于2.3节所述“辅助优化”过程新增样本点150个，其收敛曲线如图5所示。

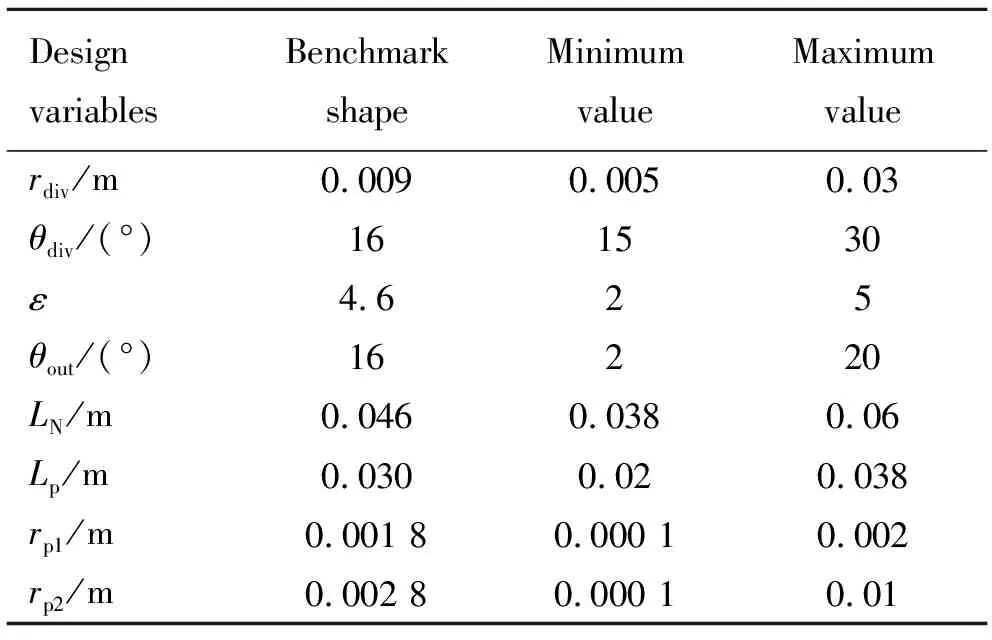
表2 设计变量取值范围及基准构型

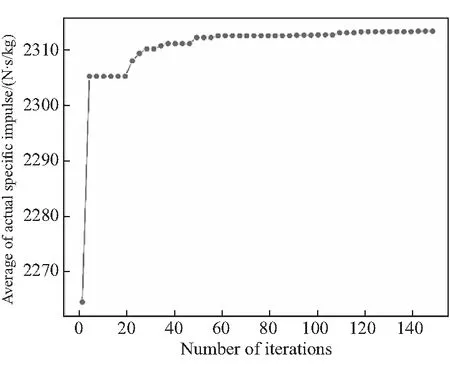
图5 收敛曲线Fig.5 The convergence curve

图6为优化前后喷管型面对比，图7为优化前后喉栓型面对比。变推力固体发动机喉栓喷管型面一体化优化设计结果如表3所示。通过对相关型面参数的优化，喉栓式喷管的由2264.536(N·s)/kg增加至2312.781(N·s)/kg，提升2.13%。

对比图8和图9优化前后流场的马赫数云图可以看出，优化后的型面使得喉栓头部下游的激波明显减弱，亚音速区域减小，这有助于减小流动过程中的损失，提高实际比冲。

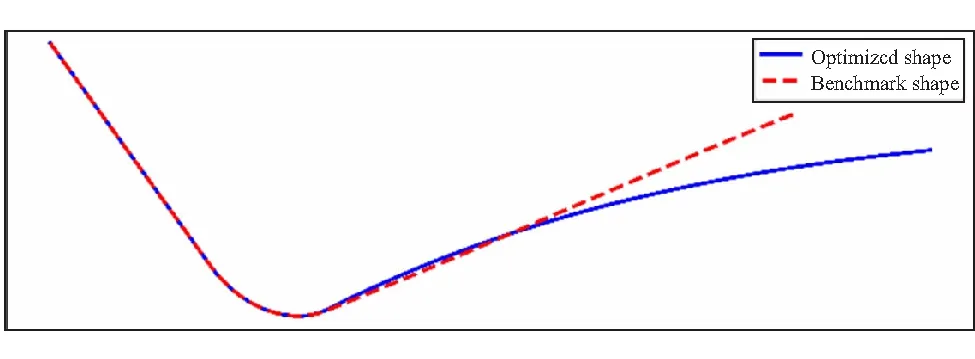
图6 优化前后喷管型面对比Fig.6 Comparison of nozzle between benchmark shape and optimized shape

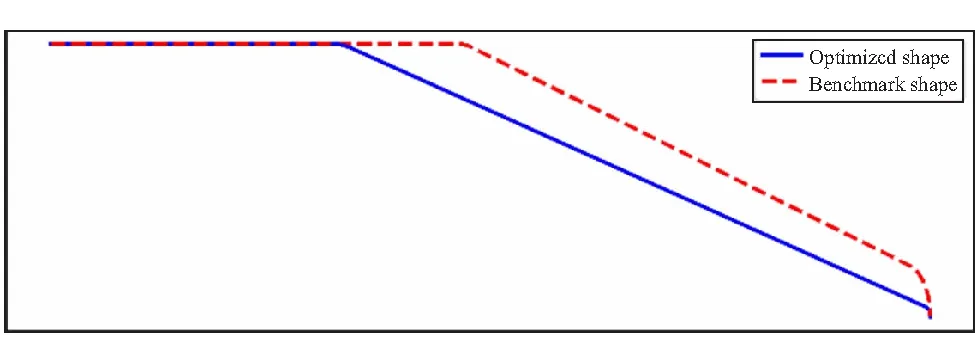
图7 优化前后喉栓型面对比Fig.7 Comparison of pintle between benchmark shape and optimized shape

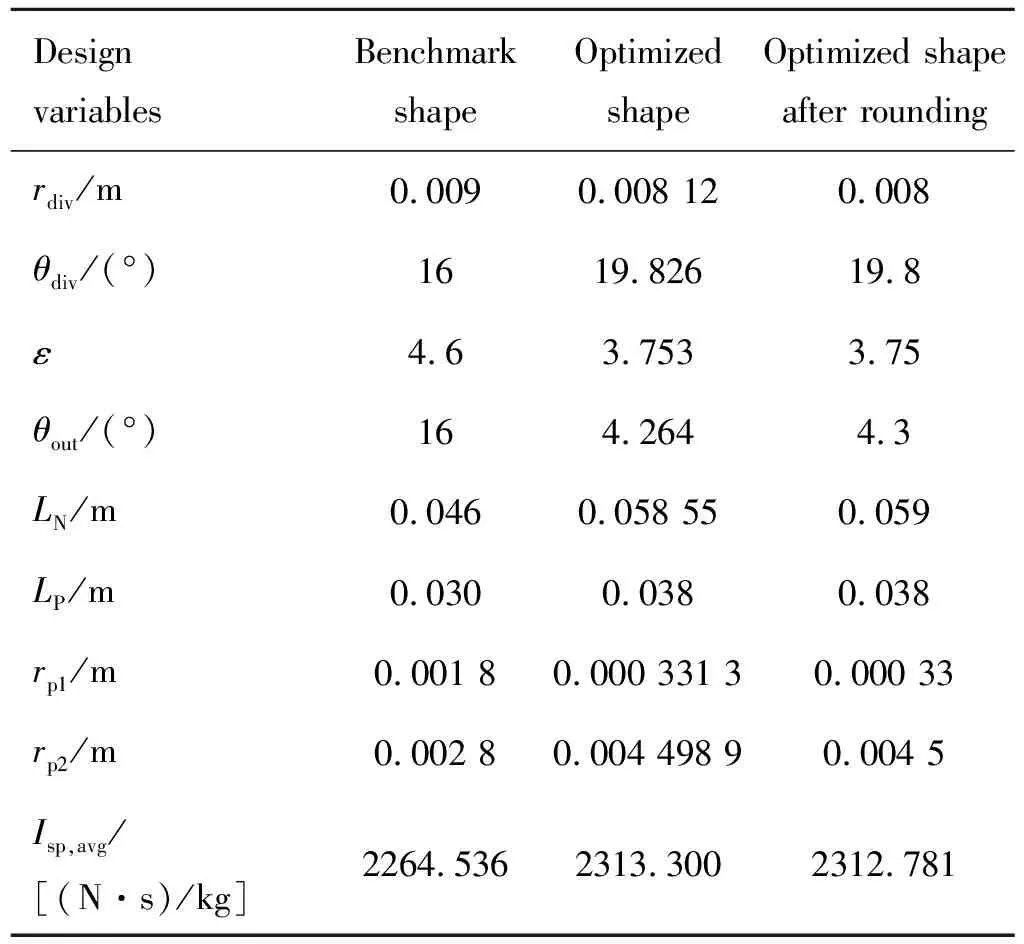
表3 优化结果对比

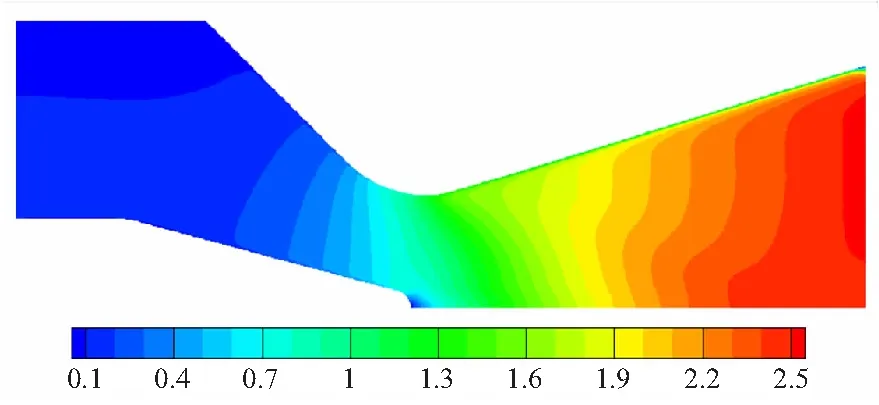
(a) Condition 1: the pintle is not inserted

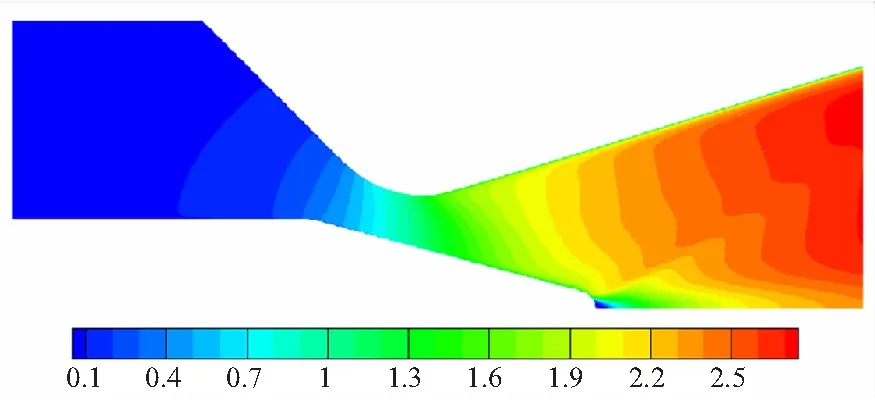
(b) Condition 2: the pintle is partial inserted

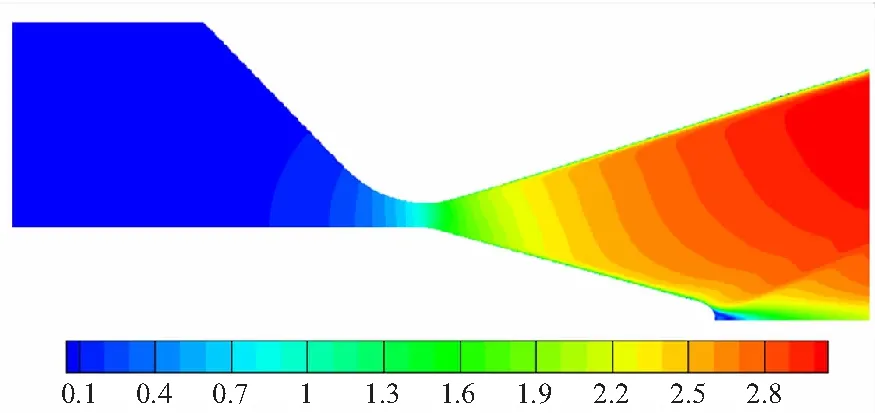
(c) Condition 3: the pintle is fully inserted

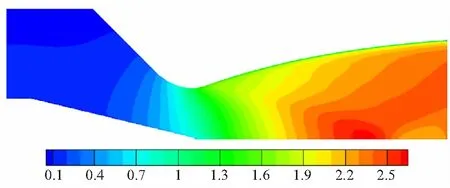
(a) Condition 1: the pintle is not inserted

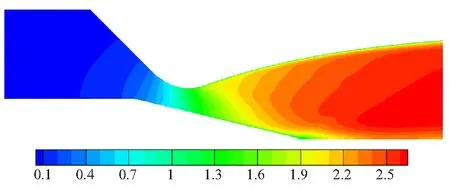
(b) Condition 2: the pintle is partial inserted

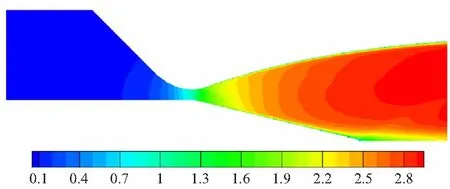
(c) Condition 3: the pintle is fully inserted

图10为喷管出口截面的径向速度分布示意图。某种程度上，发动机的比冲损失与径向速度成正相关。由图10可知，优化后型面的径向速度在三种工况下都明显减小。因此，优化后的型面能够减小流动损失，获得更高的平均实际比冲。

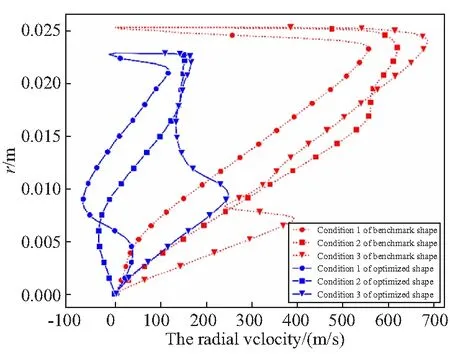
图10 喷管出口径向速度Fig.10 Radial velocity of the nozzle outlet

4 结论

(1) 本文采用优化拉丁超立方实验设计方法生成初始样本点，建立Kriging模型后，基于非精确搜索改进的增强精英保留的多种群协同遗传算法进行序列采样更新代理模型。结果表明，该代理模型优化框架能够以较少的计算量实现喉栓式喷管型面的一体化优化设计，对工程实践具有一定的指导意义。

(2) 优化后的喉栓型面头部钝度减弱，三种典型工况下喉栓下游的激波明显减弱，亚音速区域减小，符合实际物理过程。

(3) 优化后的喉栓式喷管出口截面径向速度明显减小，燃气的流动损失有所减小，发动机平均实际比冲增大，其综合性能得到改善。