基于BWI辐射效率的低气动噪声共轴对转螺旋桨的设计研究
吕昌昊 胡天翔 孙 韬 刘沛清
(北京航空航天大学陆士嘉实验室(航空气动声学工业和信息化部重点实验室),北京 100191)
0 引言
早在上世纪80年代,共轴对转螺旋桨就以其潜在的高气动效率引起科学界的关注。但是由于巨大的气动噪声,最终淡出了人们的视野。目前已知的共轴对转螺旋桨飞机也仅有苏联的图95以及乌克兰的安70,如图1所示。但是过去20年内由于燃料价格上升及航空需求的增加,共轴对转螺旋桨高气动效率以及最大起飞重量大等优势再次被人们关注。同时,气动噪声学科的发展使得降低其噪声成为可能。目前,欧盟已将其列为新一代发动机的备选构型进行研究。

(a) 图-95远程轰炸机

(b) 安-70军用运输机 图1 共轴对转螺旋桨飞机
另一方面,近年来随着环境意识增强,噪声早已被列入环境污染的一种。ICAO早已提出了逐步完善的飞机噪声标准。因此,近10年来对于对转螺旋桨的主要研究集中在气动噪声领域。主要包括用于初设阶段的气动、噪声快速预测方法,通过高精度噪声预测方法及实验方法对远场噪声机理进行研究以及降噪技术的研究。
螺旋桨噪声按照声源可以分为厚度噪声、载荷噪声以及宽频噪声。厚度噪声是由于叶片厚度周期性的排开空气产生的噪声。载荷噪声则是由于叶片上的压强分布反向作用于空气上产生的。一切随机发生的涡脱落及湍流尾迹脱落均导致宽频噪声,并且厚度噪声与周期性的载荷噪声统称为离散噪声。与单桨不同,共轴对转螺旋桨的离散噪声分为单螺旋桨噪声的独立噪声和前后桨的干扰噪声两部分。对转螺旋桨离散噪声主要噪声源按照产生机理分类,如图2所示。首先,对转桨的干扰噪声是要远超独立噪声的。而对转桨的干扰噪声又可以分为前后桨的势流干扰产生的噪声以及前桨尾迹(BWI)及桨尖涡撞击后桨(BVI)产生的干扰噪声。已有研究证实了桨间的势流干扰噪声远低于黏性尾流撞击后桨产生的噪声。

图2 对转螺旋桨噪声
随后,Horváth进一步通过实验验证了该观点并且列举出角模态(|-|)相关矩阵,如图3所示。图中横坐标与纵坐标分别为前桨和后桨在干涉频率中占的阶数,如1BPF1+1BPF2。Horváth根据辐射效率随角模态增加而减小的特性,推断干扰噪声也应有类似表现,即认为辐射效率在远场噪声中的主控性。从角模态矩阵可以看出,根据该理论的话对角线上的噪声应该较大,远离对角线时噪声衰减迅速。

图3 对转桨角模态矩阵
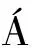
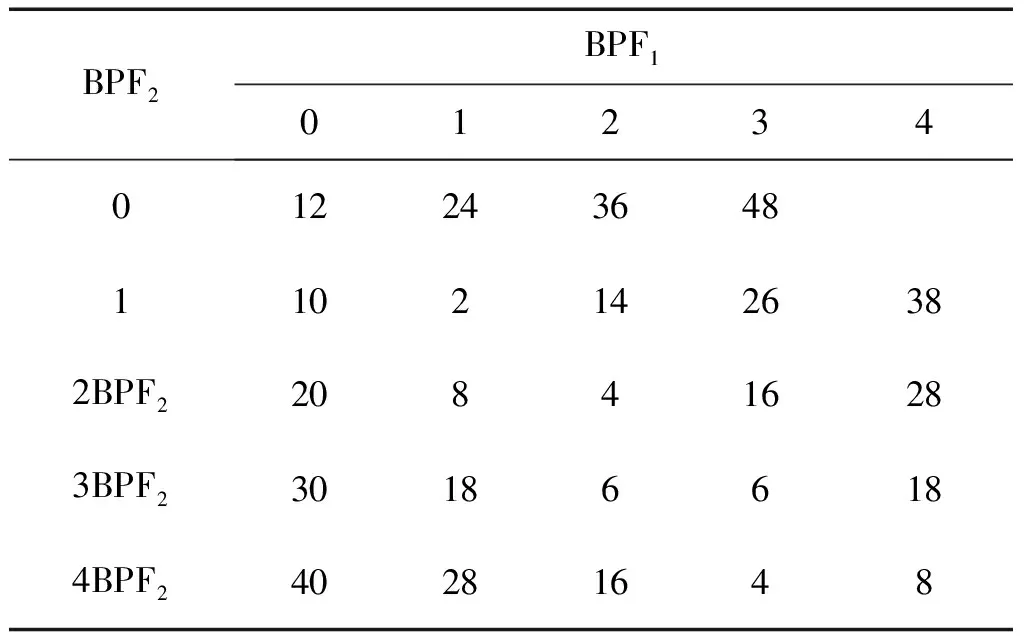
表1 12×10对转桨角模态矩阵

表2 12×12对转桨角模态矩阵
然而从角模态及辐射效率的角度考虑,不等桨叶数对转桨也可以成为很好的选择。本文通过对转桨BWI及独立噪声快速预测方法,对从低至高的(单排6-12)前后等桨叶数对转桨进行了研究。结果表明虽然低桨叶数与高桨叶数对转桨的气动噪声特性不同,但是总体上前后指向性的高声压区仍然是由BWI噪声控制。同时等桨叶数的设计只是使高声压区更集中,却无法对其进行降低。随后,对比了不同桨叶数共轴对转螺旋桨远场气动噪声的表现,认为不等桨叶数对转桨气动噪声普遍优于等桨叶数情况。
1 方法与构型
1.1 对转桨尾迹干扰噪声频域预测方法
在单桨频域噪声预测中,声压可以表示为:
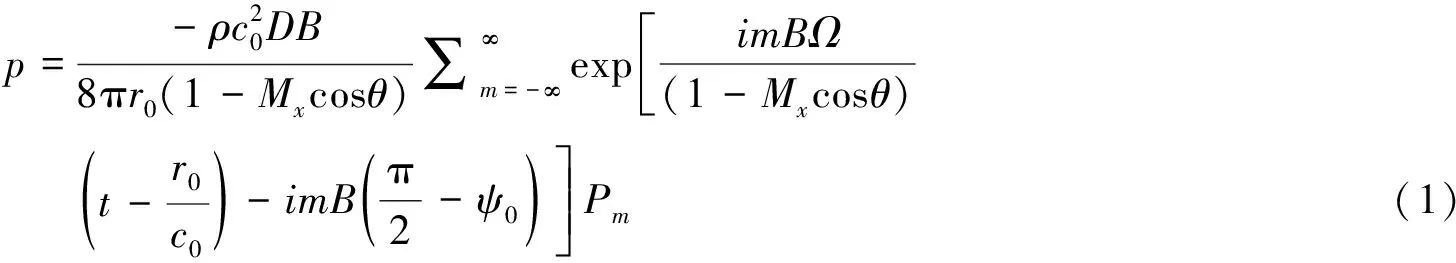
这里可以表示为:
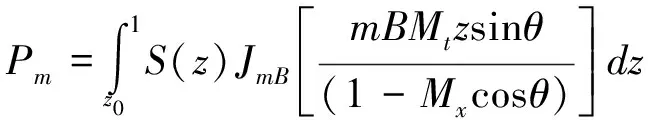
(2)
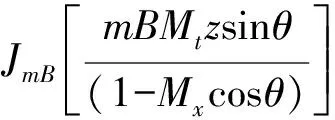
对于对转桨,同样有类似的参量定义。方程(3)和方程(4)分别为对转桨前、后桨干扰噪声公式,其中及为干扰噪声的谐波分量。

将中辐射效率以外的项均当作前、后桨径向分布的源强项()及(),则1及2如下:
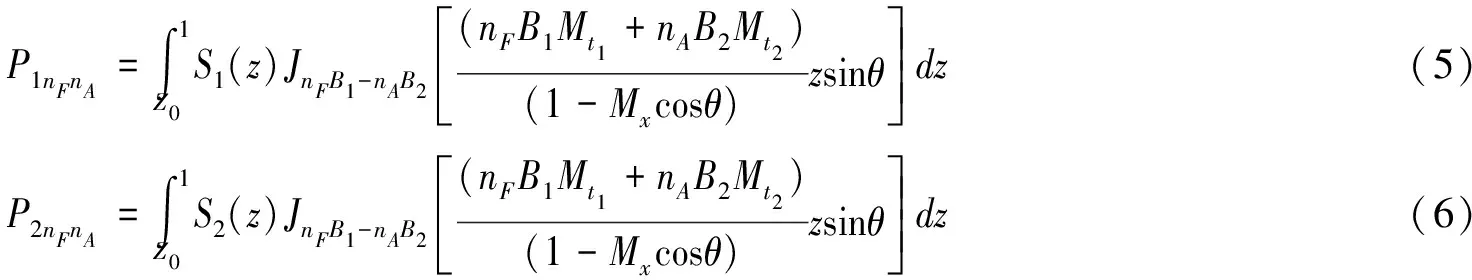
同样的,贝塞尔函数部分代表了对转桨前、后桨发出的干扰噪声的远场辐射效率,这里前后桨具有相同的辐射效率-。上述公式在使用时需要提供桨叶径向的源强项,这通常通过CFD计算或片条理论完成。本文采用共轴对转螺旋桨片条理论对桨上叶素气动力进行计算。
1.2 对转桨研究工况
本文使用的对转桨为某型6×6共轴对转螺旋桨,前后桨转速均为1 075 rpm。同时,前后桨直径为3.95 m,其几何布局如图4所示。
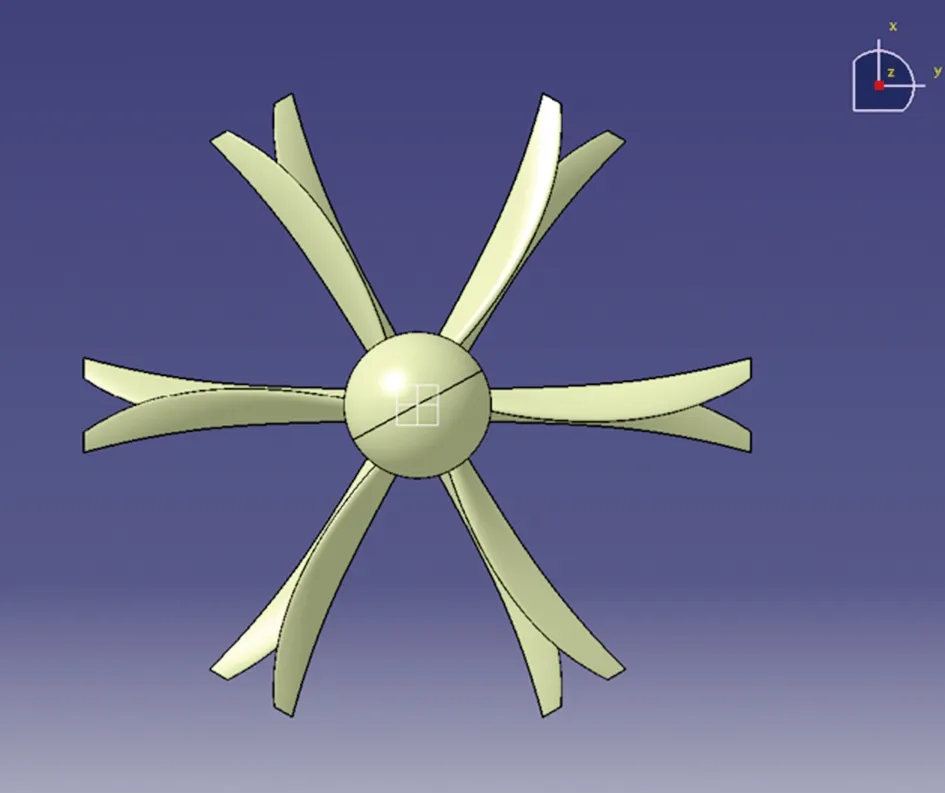
图4 共轴对转螺旋桨三维视图
对转桨噪声的研究应在保证其气动表现基本不变的情况下进行,这可以通过调整包括弦长、扭角及翼型等桨叶参数完成。本文研究使用调整安装角来调整整体扭角的方式对气动表现进行调整。研究的基准工况为6×6,前后桨安装角均为34°。其起飞气动力表现为:T = 43.0 KN, P = 3 933.6 KW。在等桨叶数研究中,对6×6、8×8、10×10、12×12在前后安装角一致的情况下进行调整,气动力与安装角见表3。这里由于基准构型为6×6,无法简单的通过调整安装角的方式得到气动表现比较接近的4×4构型,因此未对其进行研究。同时12×12桨在31°以下气动力计算发散,因此取31.1°作为研究对象。
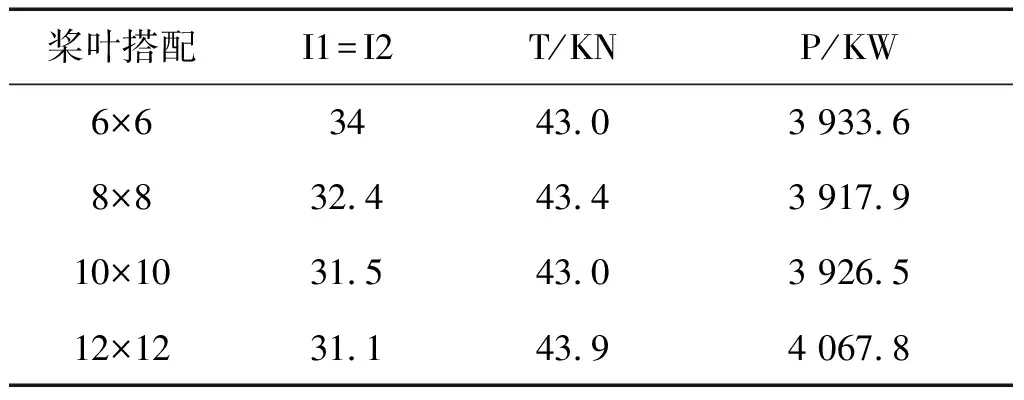
表3 等桨叶数对转桨安装角与气动表现
为了研究不等桨叶数对BWI的影响,同样需要通过调整安装角使各自的气动力表现与原等桨叶桨一致。在桨叶总数为12的情况下,不同前后桨桨叶数搭配的对转桨桨叶安装角及气动力表现见表4。
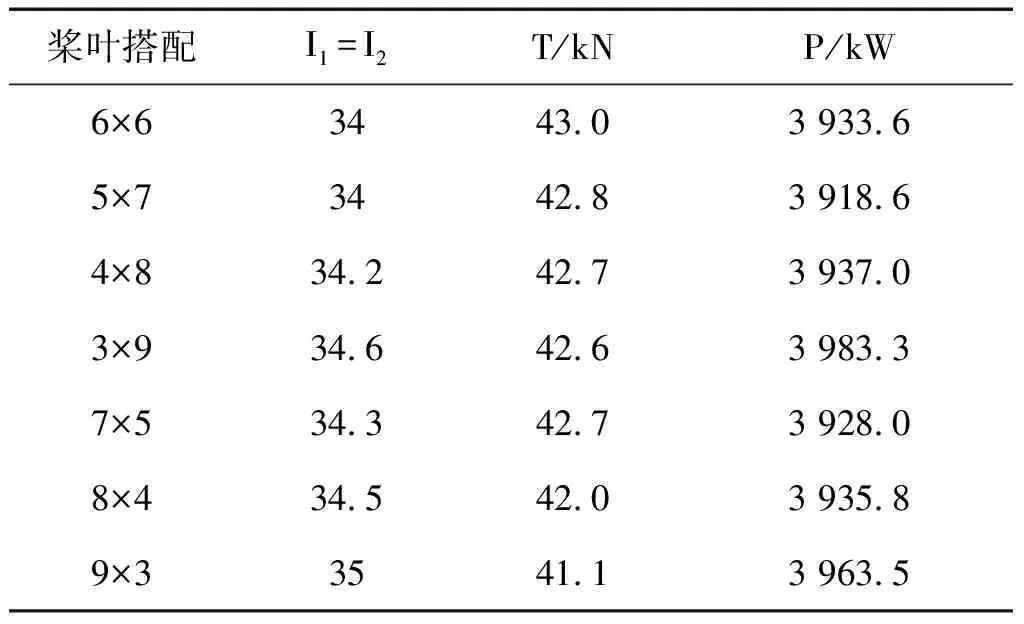
表4 不等桨叶数对转桨安装角与气动表现
2 结果与讨论
2.1 诱导角修正
上述对转桨BWI干扰噪声公式由Parry于2019年推导得出。但是在其推导过程并未考虑前桨尾迹由于诱导产生的诱导角度,如图5所示。

(a) 对转桨尾迹撞击模型

(b) 对转桨叶素三角形图5 无诱导角的BWI噪声模型
真实对转桨前桨实际入流角受到前桨自身以及后桨对前桨的诱导作用,如图6(a)所示。为此,需要在噪声计算公式中加入由片条理论计算得出的前桨诱导角度进行修正。图6(b)为考虑诱导角的BWI声压与未考虑诱导角的BWI的对比,可见诱导角对声压影响较大,不应该被忽略。
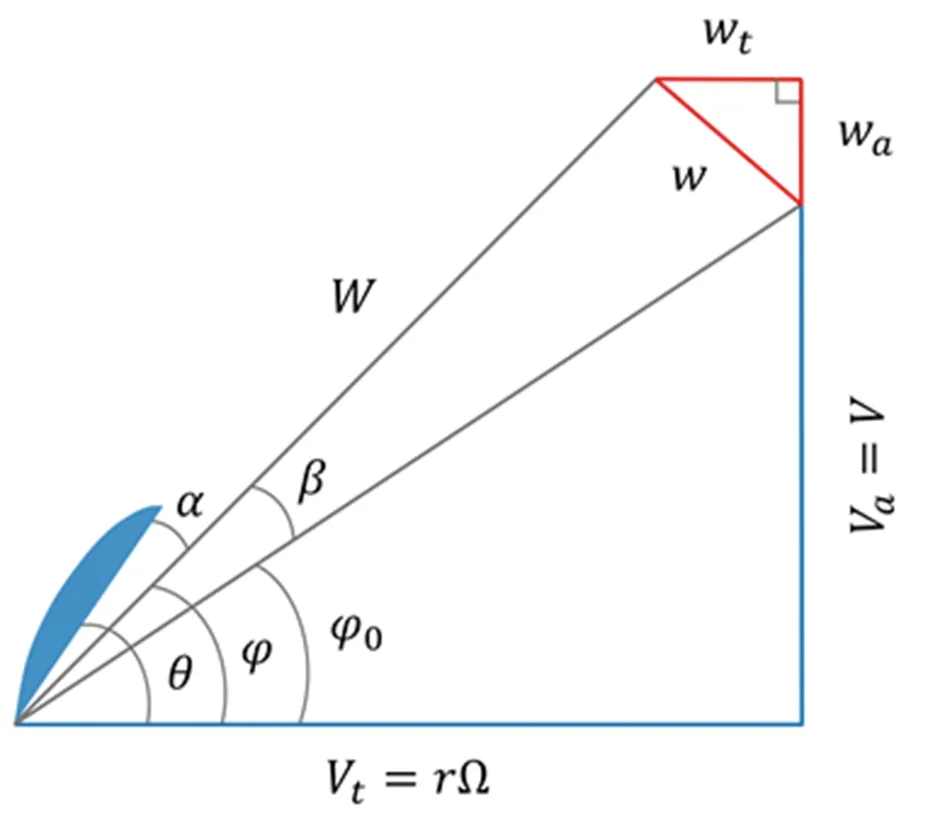
(a) 带诱导角修正的对转桨叶素三角形
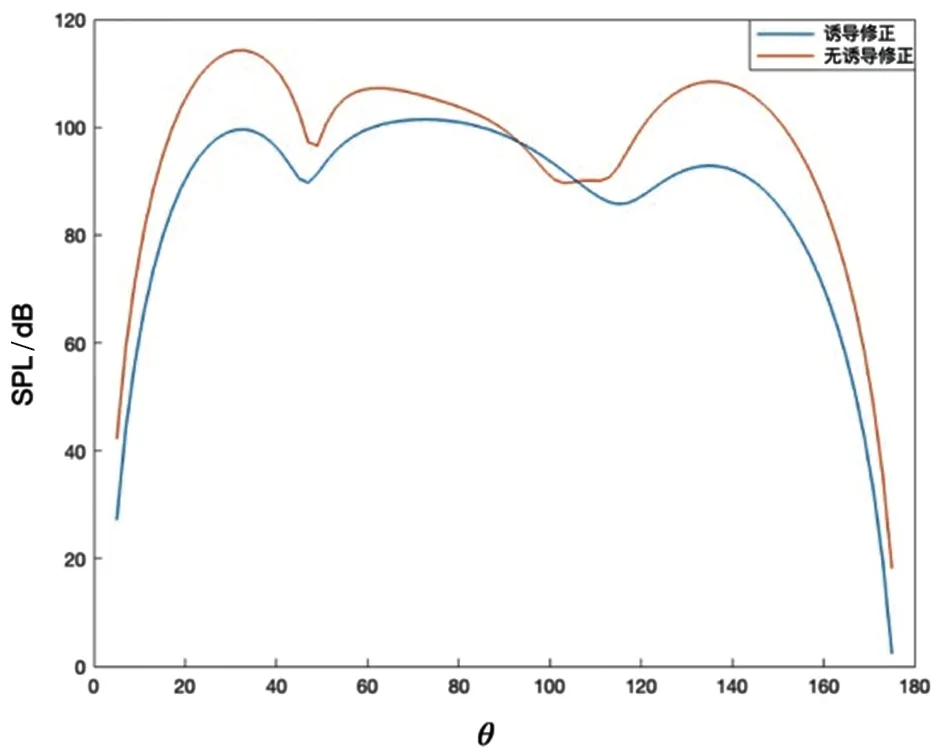
(b) 诱导角修正对BWI模型的影响图6 BWI模型的诱导角修正
2.2 等桨叶数气动噪声表现
噪声预测中,远场麦克风取在半径为10 m,间隔2°的半圆上。不同桨叶数的等桨叶数对转桨远场噪声指向性如图7所示,其中OASPL取至3阶干扰谐波。
首先,单桨独立噪声随桨叶数增加下降很明显,因此桨平面附近OASPL随桨叶数增加而减小。但是桨叶数越大,前后指向性的干扰噪声就越大。这是由于桨叶数相等时1阶谐波BWI的角模态为0,此时BWI干扰噪声辐射效率为1,噪声主要指向前后方向。这也从辐射效率的角度说明了等桨叶数的设计只能使远场噪声指向性更加集中,而不能从根本上减弱它们。
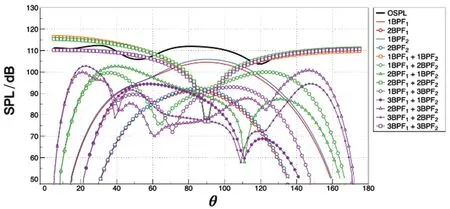
(a) 6×6

(b) 8×8

(c) 10×10
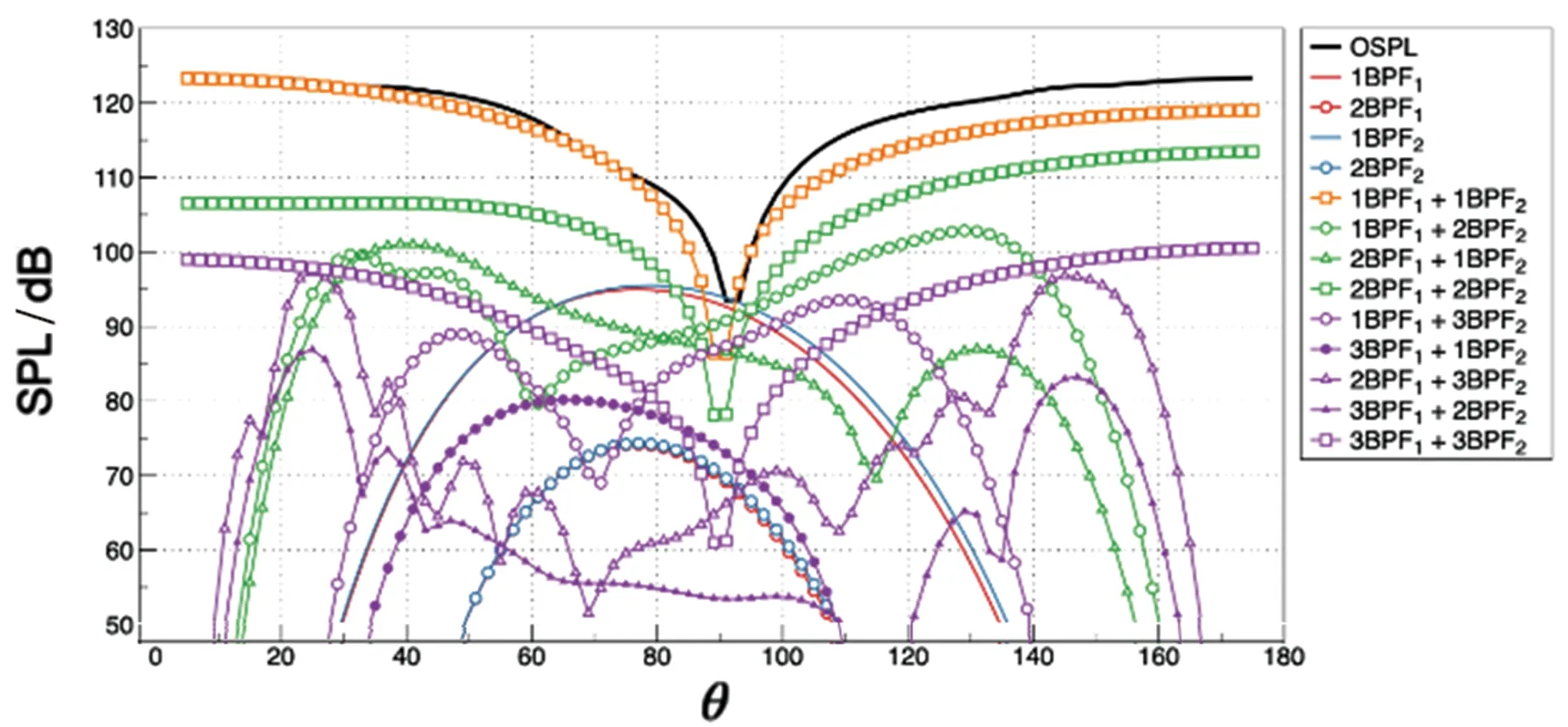
(d) 12×12图7 等桨叶数对转桨各阶谐波指向性
2.3 不等桨叶数气动噪声表现
图8为桨叶总数为12的情况下,不同前后桨桨叶数搭配的对转桨远场OASPL指向性。首先可以看到,前后桨叶数对称的构型OASPL虽然并不完全一致,但是整个指向性曲线平均来看最大声压差别不大。这说明对于前后桨叶数对称的对转桨,其BWI差别不大。同时可以看到,5×7搭配的BWI最低,而4×8搭配的BWI甚至要高于等桨叶数情况。这说明不等桨叶数搭配并不一定绝对导致噪声的降低。至于5×7搭配噪声较低原因会在下文解释。

图8 不等桨叶数对转桨OASPL指向性
图9为5×7构型各阶谐波与6×6构型各阶谐波声压对比。可以看到5×7在3阶干扰谐波以内并未出现如同6×6类似的前后非常高的干扰噪声,这是由于该类干扰噪声是由于对应频率的角模态为0导致辐射效率为1而引起的。对于5×7构型,其角模态为0的干扰频率最早出现也要在7BPF+5BPF时才会出现。图中特意对直到7阶干扰噪声的OASPL进行了计算,结果证实对于5×7构型即使包含了角模态为0的干扰噪声,其总声压级也不会显著提高。这是由于7阶干扰噪声自身随谐波的衰减导致的。同时,7BPF+5BPF仍然处在高水平也从侧面证实了辐射效率对远场噪声主控地位。
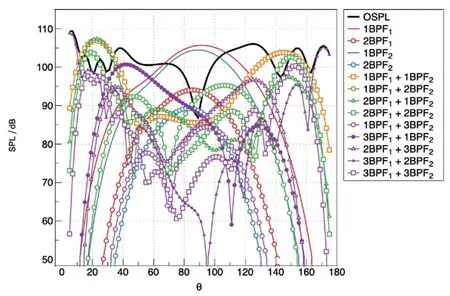
图9 5×7对转桨各阶谐波指向性
3 结论
本文首先介绍了对转桨噪声的类别。随后从对转桨BWI频域快速预测方法出发,引入了诱导角对该公式的影响。并对比了有无诱导角时对转桨声压指向性的差别。
前后等桨叶数情况下,对转桨离散噪声的OASPL随桨叶数有不同特性。桨叶数很大时,BWI干扰噪声对OASPL起主要贡献。随着桨叶数的降低,独立噪声对旋转平面中部指向性贡献增大,主控该区域OASPL。
辐射效率对共轴对转螺旋桨的BWI起着绝对的主控作用。前后桨叶数相反6×8、8×6的构型,OASPL相差不大。从桨叶数的角度考虑,对转桨应该尽量去选择前后桨叶数能满足角模态为0的干扰噪声出现在更高的阶数这一条件。后续研究将集中在通过高精CFD与FWH相结合的混合算法对对转桨桨叶数对对转桨的气动及噪声的影响进行更深入的研究。

