考虑滞回效应的锂离子电池二阶电热耦合模型∗

史永胜符 政刘博亲左玉洁王 凡

(陕西科技大学电气与控制工程学院，陕西 西安 710021)

锂离子电池是混合动力汽车(HEV)和全电动汽车(EV)中最常用的清洁无污染储能能源。它具有高能量密度、无记忆效应、长循环寿命等相对于其他电池的优良特性[1]。在研究和开发锂离子电池时，由于锂电池的非线性特性，使用稳定、精确的电池模型在应用层面显得至关重要[2]。

目前主要有三种电池模型:数据驱动模型、物理模型[3－4]以及等效电路模型，由于等效电路模型它的参数化复杂度较低，计算速度快，而被广泛使用。这种模型由基于充放电状态的开路电压(Open Circuit Voltage，OCV)、RC 对，以及欧姆电阻组成[5]，但这种电池模型没有充分考虑滞回效应以及温度环境对电池的作用。Zhang Ruifeng 等人[6]发现，电池工作温度对OCV 荷电状态特性有显著影响，因此，为了提高模型的精度，提高电池状态估计的精度，需要考虑温度因素。Roscher Michael A[7]在研究中指出，锂电池会表现出OCV 滞回特性，由于充放电调整后OCV 值的差异，所以会对电池建模以及电池状态估计问题造成影响。文献[8]描述了一种考虑温度因素的二阶RC 电池等效模型，但模型未考虑电池的极化效应，导致模型仍存在不小误差。而文献[9]对锂离子电池的迟滞行为进行了研究和建模，但模型未考虑不同温度下电池状态，模型也具有一定的局限性。

目前，锂离子电池主要用作电动汽车的中央动力部件，为了有效使用锂离子电池，通常需要精确的电池单元建模[10]。针对以上提出模型存在的局限性，文章在宽温度范围内，选择依赖于温度的电池建模方法，通过将滞回效应由单态滞回模型进行模拟，用于更精确地估计系统电压的参数，将二阶阻容等效电路模型与单态滞回模型结合，再与二态集总参数热模型进行耦合，利用不同温度下城市道路循环工况(Urban Dynamometer Driving Schedule，UDDS)工况实验，以及MATLAB 参数拟合工具箱模拟，对电池模型参数进行辨识。最后将不同温度下的模型输出端电压与真实值比较，最终得出所提出带滞回效应的电热耦合模型的高精确性。

1 锂电池电热耦合模型

1.1 等效电路模型

本文选择的等效电路模型为二阶RC 网络模型，用以捕捉锂离子电池的电气动态特性[11]。一般来说，该电路的阶数越高，即RC 对越多，模型的精确度越高，但其模拟实际电池工况时，软硬件计算的速率将大大降低。这种建模方法依赖于经验系统识别技术和实验数据。图1 为所提出的等效模型:

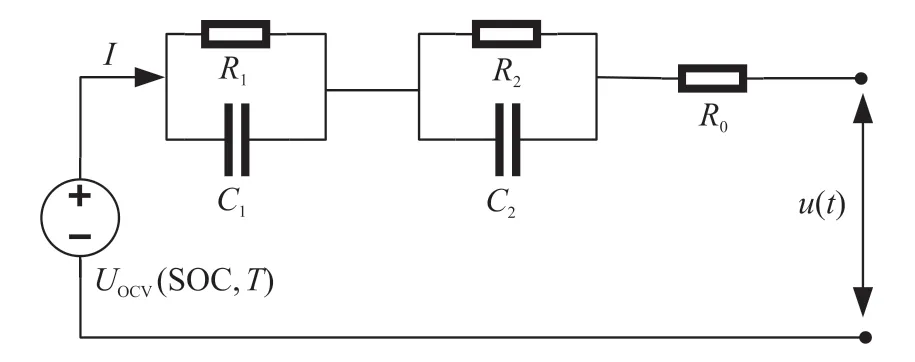
图1 二阶等效电路模型

图中，UOCV(SOC，T)表示开路电压OCV，它的值取决于电池荷电状态(SOC)和温度T。I和u(t)分别表示输入电流和端电压。该等效电路模型包括2个RC 对，每个RC 对由并联的Ri(电阻i)和Ci(电容i)组成(i＝1，2)，它们的值也随着SOC 与温度的波动而不定，其中R1、C1分别指代了电化学的极化R和极化C，R2、C2分别指代了浓差极化R和浓差极化C。在图1 中，R0代表电池的欧姆内阻。对于这个锂离子电池的模型，使用输入电流I和端电压u(t)的实验数据对图1 的等效电路进行建模。

我们定义电池完全充电时，SOC ＝z(t)＝1，当电池完全放电时，SOC 定义为z(t)＝0，将电池从z(t)＝1 放电至z(t)＝0 时消耗的电荷总量定义为总容量Q(以Ah 为单位)。因此，SOC 定义为:

以采样周期Δt采样并包括效率因子η(t)，将式(1)离散化得到:

其中效率因子η(t)称为“库仑效率”，充电时为ηk≤1，放电时ηk＝1。由等效电路结合基尔霍夫电压定律可得:

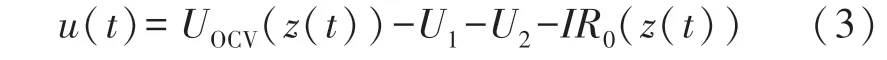
式中:UOCV代表开路电压，U1、U2代表两个RC 对的压降，IR0代表欧姆内阻压降。

1.2 滞回效应

如图2 显示了在相同电流值，充电和放电的情况下，25 ℃时OCV 的比较。图中显示，在相同的SOC 下，充电OCV 曲线一直比放电OCV 曲线高，这说明OCV-SOC 的关系不是一对一的映射。由于电池的静置，电池的端电压将收敛到OCV，所以图中的这种现象即表明，锂离子电池的端电压存在滞回效应[12]。

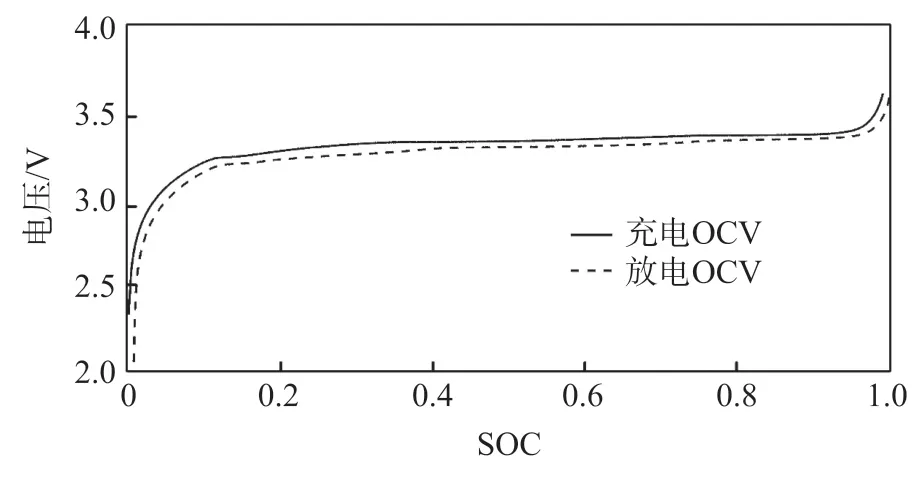
图2 实验得25 ℃下OCV 与SOC 关系

对于一些锂离子电池，如LiFePO4，如果电池模型不包括滞回效应，则SOC 的估计误差会增大。因此在以往的等效电路模型的基础上，本文采用滞回电压来反映滞回效应，从而提升模型的精确度。

表示滞回可以分为两种不同的模型，一种是:“零状态滞回模型”，另一种是:“单态滞回模型”。对于零状态滞回模型，只需要在状态空间表示的输出方程中添加一项:

式中:R0表示电池内阻，ik表示第k个时间步长的电流，sgn()是符号函数，用以判断充放电信号，M表示滞回电压。但零状态滞回模型仅仅表示出完全充电和完全放电周期期间捕捉到的充电和放电之间的差异，而在实际的循环中，频繁的充电和放电会产生微小的环路，由于电流频繁的符号变化，sgn(ik)M(zk，Tk)也会经历同样复杂的变化[13]。但实际上，滞回电压是逐渐增加或减少的，并不是瞬时改变。单态滞回模型则可以捕捉到滞回电压逐渐衰减或增加的现象，以及不同荷电状态下衰减速率的变化[14]。将滞回相关状态与SOC 关系由式(5)给出:

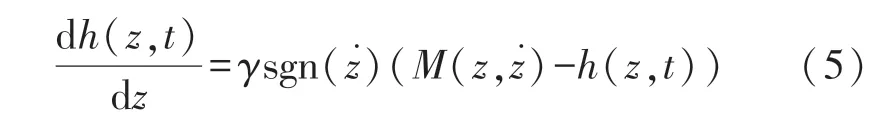
式中:h(z，t)称为滞回电压，M(z，)是SOC 与SOC变化率的函数，它表示滞回效应引起电池的最大极化电压。方程中的M(z，)－h(z，t)项表示滞回电压的逐渐增加或衰减，γ是用于调节衰减率的正值常数，它使得方程在充电和放电时都是稳定的。将等式两侧同时乘以dz/dt，使等式从关于SOC，处理为关于时间t的微分方程，再使用链式法则变形得:

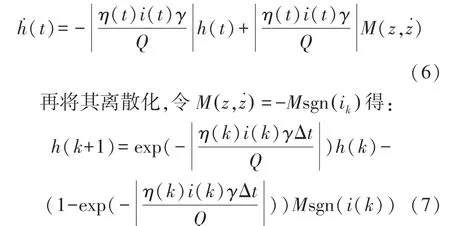
假定在充电和放电情况下，最大滞回电压M分别为负常数和正常数[15]。在式(7)中，如果输入电流i(k)足够小，最大滞回电压M即为零。除了随着SOC 的变化而变化的动态滞回效应之外，还经常看到在电流符号变化时，建立瞬时变化滞回电压模型可以带来的模拟优势。由定义式(8)得到瞬时滞回电压为M0s[k]，滞回电压即可表示为等式(9)。从文献[16]得到的滞回电压数据可以看出，在5%～95%的电池工作范围内，滞回电压值随SOC 的变化不大，可以将滞回电压定义为与温度相关的变量。

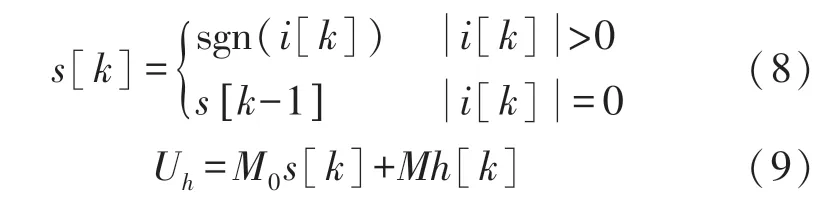
将滞回电压包含在等效电路模型中，等式(4)可扩展成如下:

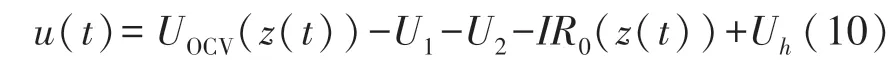
式中:Uh表示滞回电压，这样我们可以得到如图3改进过的等效电路模型。

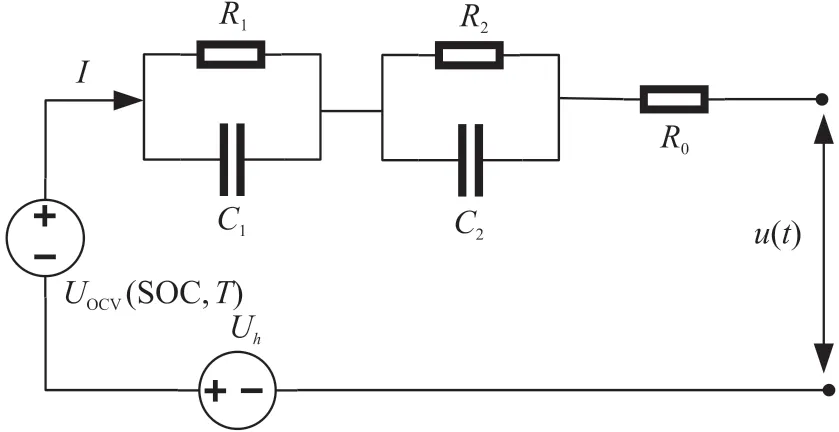
图3 带滞回效应的等效电路模型

就计算复杂程度而言，所提出的等效电路模型并不复杂，在计算量适当的同时，实现了捕捉模型动态的合理性以及真实性。

1.3 二态热模型

本文采用了简化的二态热模型来捕捉圆柱形电池的核心和表面温度，此模型假设发热位于电池核心，中心的热通量为零，在文献[17]中，为了评估表面温度均匀性假设的有效性，对电池侧面和末端表面进行了红外成像，结果表明，不同表面之间的温差在2 ℃以内，证明了二态热模型的合理性，所以可以假设热量传递均匀，沿电池高度的温度变化被忽略。如图4 所示为所搭建模型原理图。定义式写为:

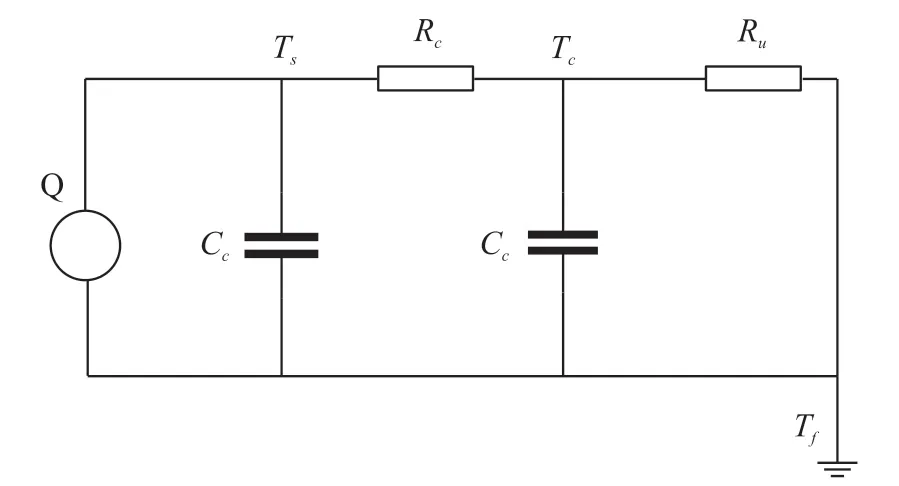
图4 二态等效热模型

式中:Ts、Tf、Tc分别表示电池表面温度，环境温度以及核心温度，Q代表电池芯中的发热量，等效热传导电阻Rc是一个集总参数，它集合了致密和不均匀材料的导热和接触热阻，并模拟了电池芯和表面之间的热交换。电池表面和周围冷却剂之间的热交换由等效对流电阻Ru模拟。在一些电动汽车应用中，冷却剂流速是可调的，用以控制电池的温度，这使得Ru的值随着冷却剂流量的变化而变化，但在本文实验里，冷却剂流量，即环境空气保持恒定，以使Ru不变。Cc是电池极组的热容，模拟电池核心的温度变化率，Cs是电池外壳的热容，模拟电池表面温度的变化率。设采样时间为Δt，将式(11)离散化得:

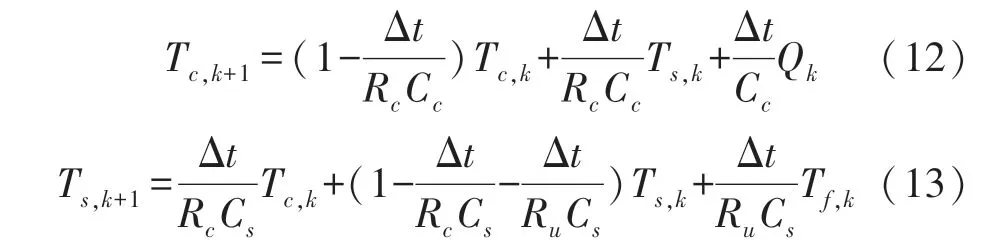
1.4 电热耦合模型

所建立的电模型和热模型之间的电热耦合是通过式(11)中的发热项Q来实现的，锂离子电池的发热表达式如下:

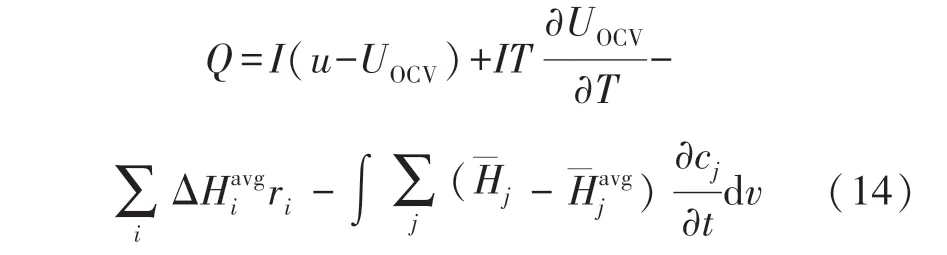
式中:I是电池电流，u是电池电压，T是温度，ΔHi表示化学反应i的焓变，ri表示i的反应速率，表示样品j的偏摩尔焓，cj表示浓度，t代表反应时间，v代表反应量，上标avg 表示在体积平均浓度下的评估性能，∂UOCV/∂T表示温熵系数，即开路电压温度系数。第一项模拟不可逆的发热，即焦耳加热和电极上的能量耗散。第二项模拟熵热，第三项是所有化学反应产生或消耗的热量，最后一项表示电池内浓度梯度和滞回过程中产生的混合热。因第三、四项对电池产热影响很小，可忽略。

电气子模型和热子模型通过双向耦合相互作用，如图5 所示。

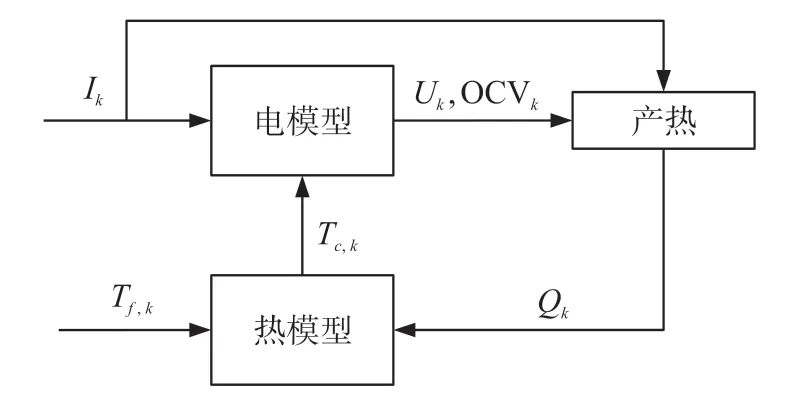
图5 电模型与热模型耦合过程

首先，等效电路模型基于输入电流I，和电参数R0，R1，R2，C1，C2计算电池的SOC，OCV 以及端电压，利用电模型得出的参数和输入电流确定发热量Q，然后热子模型基于Q和环境温度Tf计算核心温度Tc和表面温度Ts，Tc代表电池集总电极组件的温度，用于确定电模型的温度相关参数。

2 模型参数辨识

2.1 等效电路模型参数辨识

为了辨识出电模型的参数，首先需要确定不同温度下OCV 与SOC 的关系。本文对锂电池进行了实验测试，在测试开始之前，将电池充满电，然后电池非常缓慢地放电至最小工作电压，同时连续测量电池电压和累计放电安培小时数，之后电池再非常缓慢地充电至最大工作电压，同时连续测量电池电压和累计充电安培小时数。

将收集的数据进行处理，得出OCV 与SOC 的曲线。假设从真实OCV 到放电OCV 和充电OCV曲线的偏差在数量上相等，因此我们将电池的真实OCV 近似为这两个值的平均值。同时由于使用非常低的电流速率，电池中产生的热量可以忽略不计，而电池的库伦效率在不同温度下并不一致，计算25 ℃的库伦效率[18]:

不同温度下的库伦效率为:

计算各个温度下的库伦效率得出如图6，可见库伦效率在不同温度下差距不大，提升计算效率可近似为1。

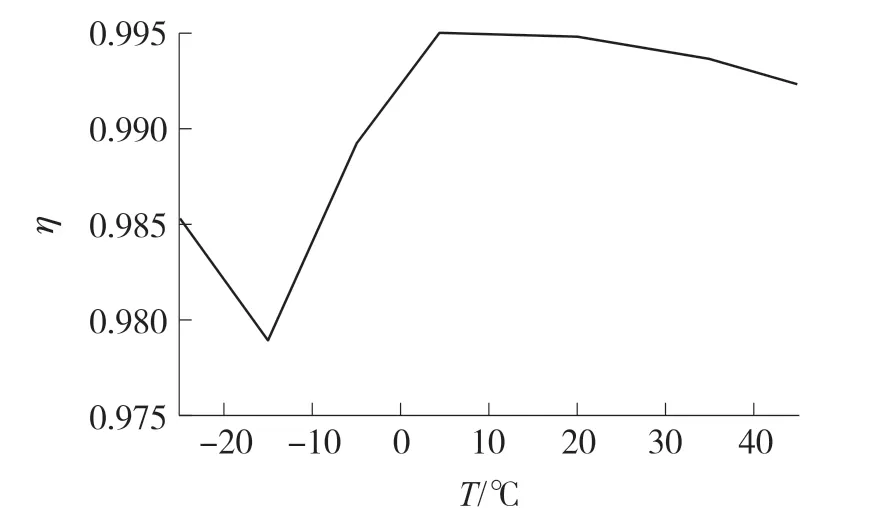
图6 不同温度下库伦效率

2.1.1 OCV(SOC，T)参数

如图7 所示，为分析实验得出35 ℃情况下OCV-SOC 关系图，计算出不同温度下每个数据样本对应的SOC，即可得到图8 各个温度下OCV-SOC 的关系曲线。

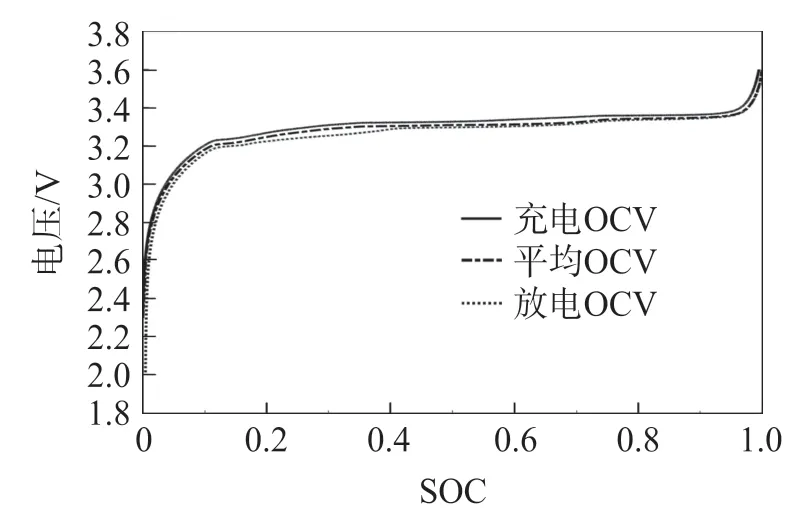
图7 35 ℃下OCV-SOC 关系图

图8 各个温度下OCV-SOC 的关系图

将测量得到的数据，利用MATLAB 中的CFTOOL拟合工具箱进行曲线拟合，拟合函数为:

式中:P1～P8为温度相关拟合参数，将不同温度下的OCV-SOC 曲线进行拟合，得到如表1 所示的参数，R-square为确定系数，可以看出系数皆逼近于1，说明曲线拟合程度较好。再将得到的数据通过MATLAB 的surf 函数进行处理，得到OCV(SOC，T)图，如图9 所示。

表1 锂离子电池SOC-OCV 拟合参数

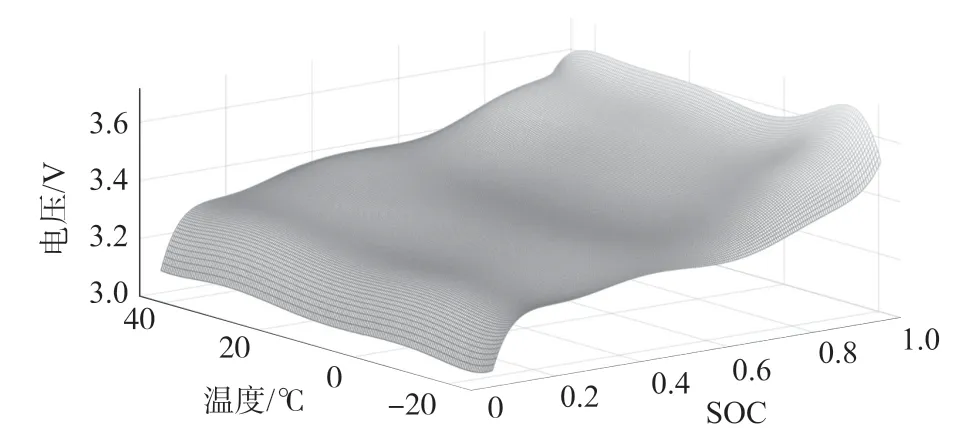
图9 OCV(SOC，T)三维曲面图

2.1.2 阻容参数

为了获取欧姆内阻和RC 对参数，进行了(Hybrid PulsePower Characteristic，HPPC)实验。实验得到电池的电压曲线如图10 所示。R0的计算是通过欧姆定律实现的，即通过图10 中的U1～U4以及HPPC 实验脉冲放电时的放电电流值Id，经式(18)得到:

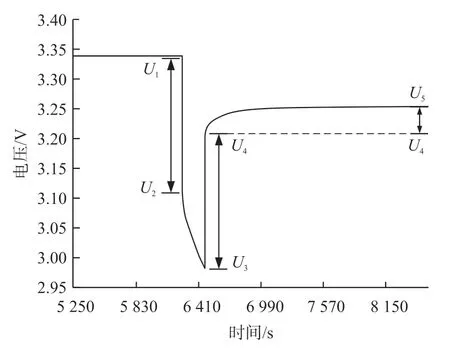
图10 HPPC 工况实验电池电压曲线图

将不同温度下的实验数据通过计算输入至MATLAB 中cftool 工具箱进行拟合，将得到的曲线利用节1.1 所述方式进行拟合，得到如图11 三维曲面图。

图11 不同温度下R0 计算结果

由于电化学极化R1和C1以及浓差极化R2和C2可以由电池放电后静置区间的测量数据进行计算得到，如图10，利用U4～U5范围的数据对电池放电的极化R1、R2和极化C1、C2进行计算，计算方法如式(19):

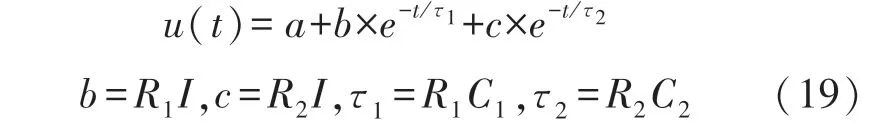
式中:u(t)，t，I分别表示电池静置区间内t时刻的端电压值，时间，电流值。利用cftool 工具进行拟合曲线得到对应b，c，τ1，τ2的值，利用上式计算出电化学极化RC 以及浓差极化RC，最后将不同温度下的实验数据进行与R0同样的数据处理，得到三维曲面图如图12 与图13。

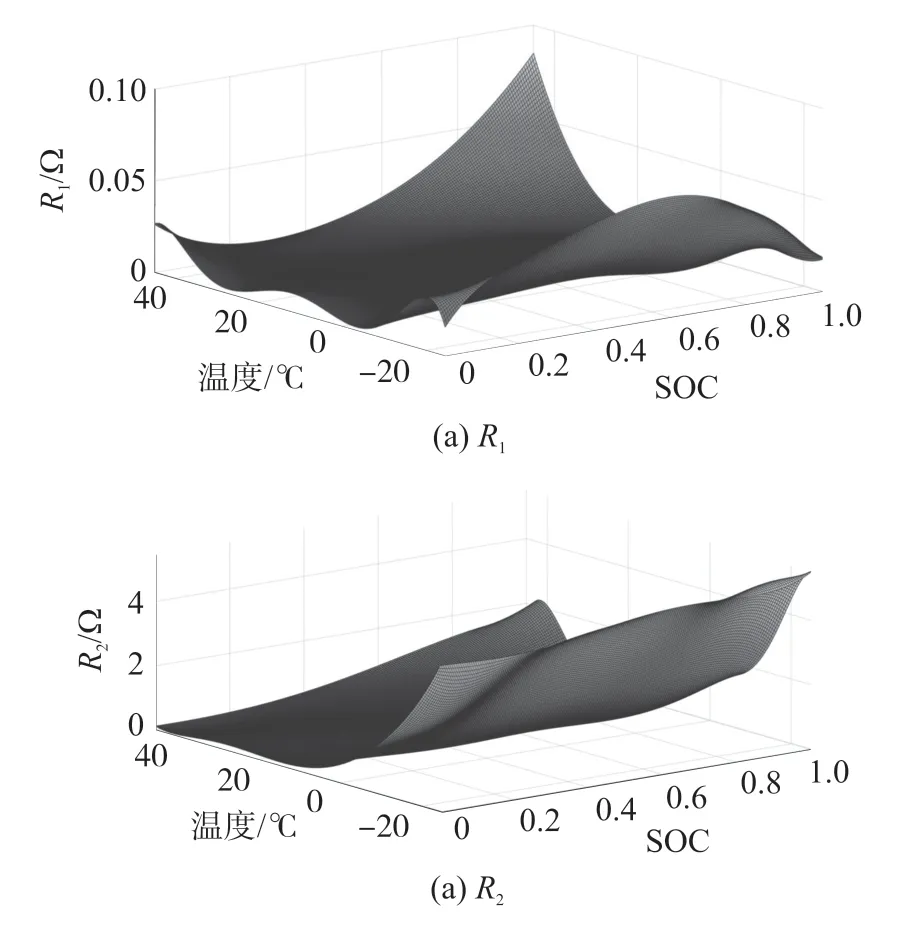
图12 不同温度下R1、R2 计算结果

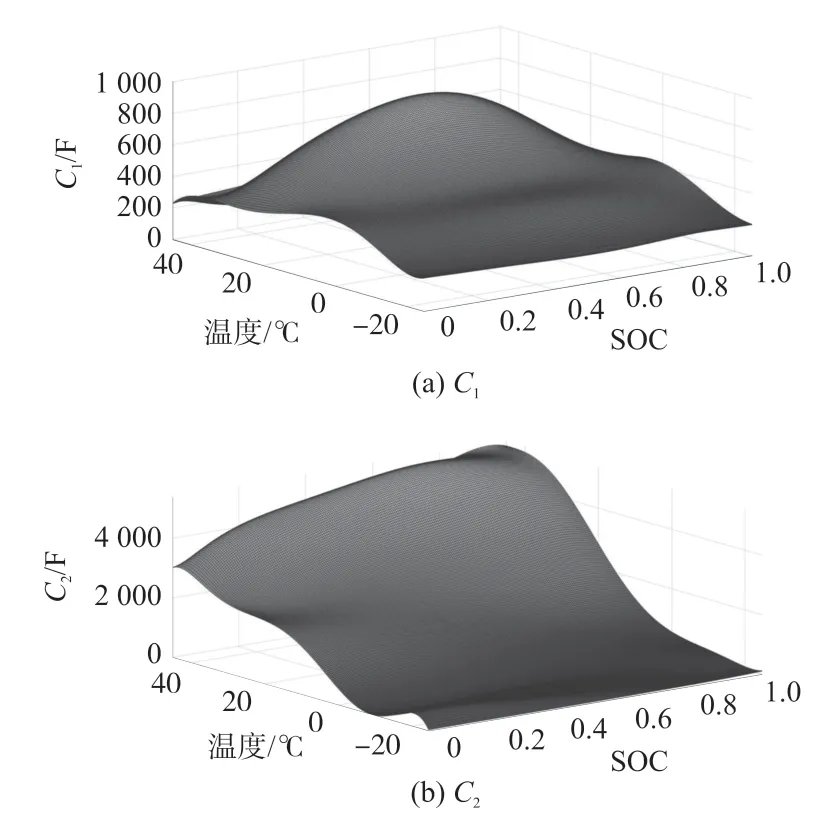
图13 不同温度下C1、C2 计算结果

由得到的实验结果可知，在不同的温度、SOC下，极化RC 与欧姆内阻R0的数值均会发生不同的改变，可见模型参数对当前时刻电池温度、SOC 准确度要求较高。对于模型参数将采用MATLAB 中2-D Lookup Table 模块加以实现。

2.1.3 滞回参数

由于以往的电模型辨识滞回电压较为困难且计算复杂，本文将采取MATLAB 参数拟合工具箱来得到其滞回参数值。将文章第一章中SOC 定义式(2)，滞回电压关系式(7)、(8)、(9)以及RC 对关系式(10)结合，利用MATLAB 的Simulink 搭建出等效数学模块电模型，如图14。

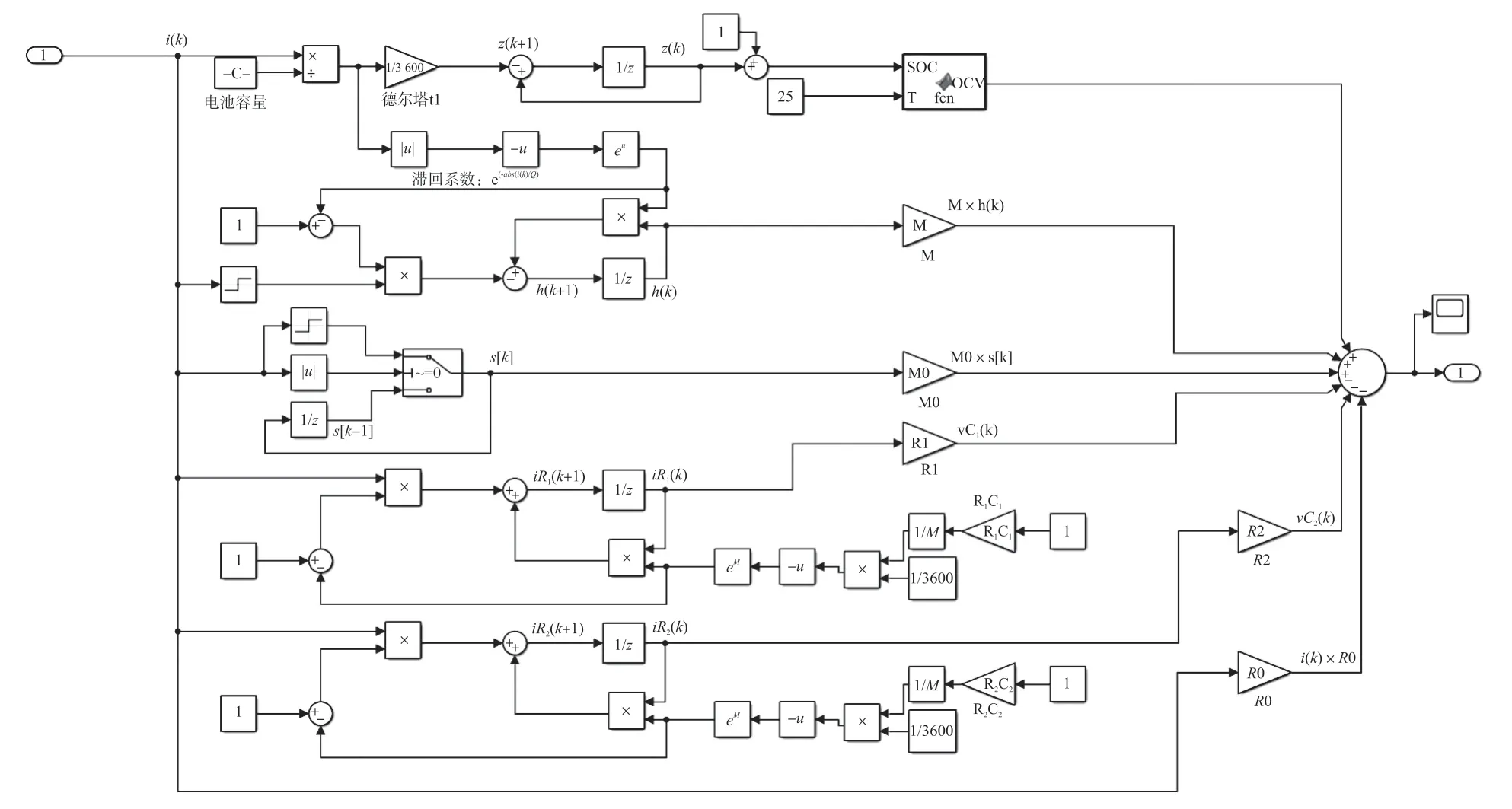
图14 Simulink 参数拟合使用模型

通 过 MATLAB/Simulink 中 的 Parameter Estimator 软件进行仿真迭代，将得到的仿真数据进行拟合，得到图15 中M、M0与温度T的函数关系。

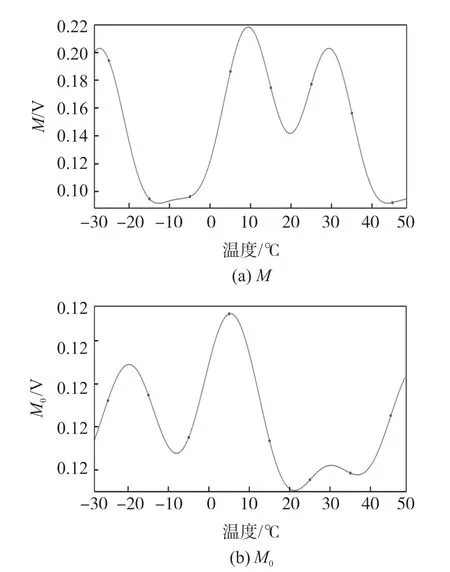
图15 M、M0 与温度的关系曲线

2.2 热模型参数辨识

由第一部分的2.1 节可知，所建立的二态热模型需要辨识的参数等效热传导电阻Rc，等效对流电阻Ru，电池极组的热容Cc以及电池外壳的热容Cs。假定表面热容量Cs是已知的，因为它可以根据外壳的比热容和尺寸很容易地计算出来[19]。Cs的值近似等于4.5 JK－1[20]。为了识别热模型的集总参数，需要根据以下离散时间参数模型重新排列模型方程:

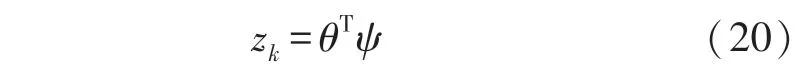
式中:z为观测值，θ为参数值，ψ为回归量，由实测信号组成。参数模型可以将方程(12)和(13)结合起来导出。利用实验得到测量信号I，u，Ts和Tf代替未测量堆芯温度Tc，假定Tf被调节为常数，Tf，k＋1等于Tf，k，所以可得到式(21):

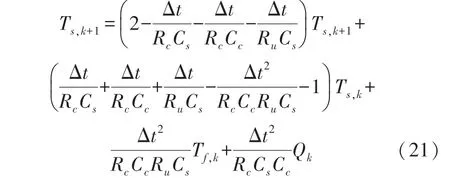
设α，β，γ，δ分别为式(21)各项系数，可得z，θ，ψ的表达式，基于参数模型，将最小二乘法用于估计集总参数，可得式(22):

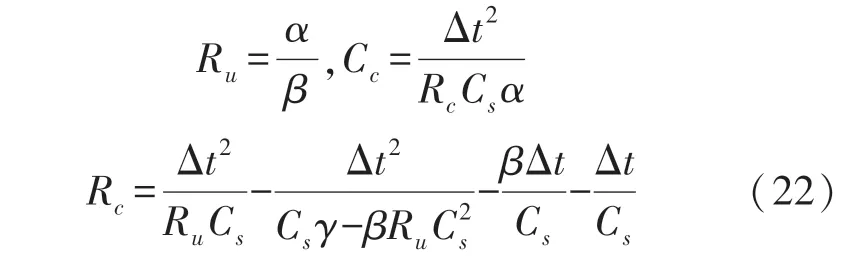
为了使用这里提出的方法确定热模型参数，进行了实验室实验。将电池放在温度调节至25 ℃的热室内，表面安装热敏电阻进行测量。在实验装置中，室内的空气温度被认为是热模型中的冷却剂流动温度。以这种方式，第二个热敏电阻被放置在电池旁边的热室内，以捕获周围的温度。使用功率放大器向电池施加频率为0.05 Hz、幅值为20 A 的对称周期性电流脉冲，以提高电池的温度，脉冲是对称的，以便随着时间的推移保持电池处于平均充电状态(50%)。之所以选择此SOC 值，是因为它是许多应用中使用的平均值(这是针对电池表现出最大充电/放电功率的SOC 周围的工作条件)。图16 描述了用于提高电池温度的输入电流脉冲，电流施加一小时三十分钟，然后关闭以允许温度松弛。使用数字示波器记录两个热电偶的输出电压并进一步转换为温度。

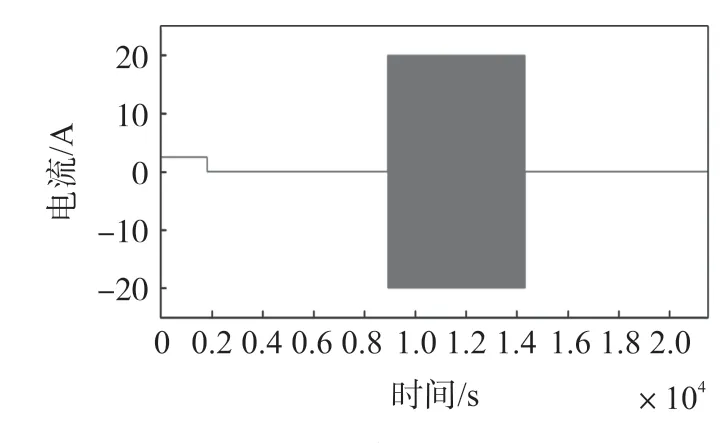
图16 用于热模型参数识别的输入电流

最后基于实验得出热模型参数，如表2 所示。

表2 二态热模型辨识参数值

对于电热耦合关键的温熵系数∂UOCV/∂T，利用热循环中SOC ＝0.5 时的OCV 变化曲线，温熵系数通过将曲线拟合成U(T)＝A＋BT＋CT2，其中A、B、C是常数，B对应温熵系数∂UOCV/∂T，如图17。

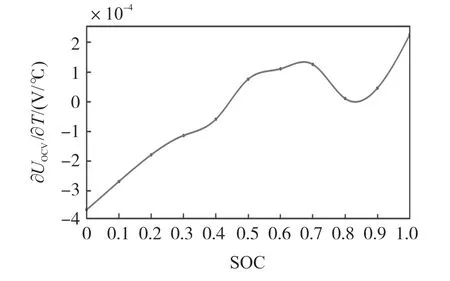
图17 温熵系数∂UOCV/∂T

基于以上的参数辨识，可将考虑滞回效应的等效电路模型与二态热子模型进行耦合。

3 仿真及实验结果分析

文章以A123 26650 型号的ANR26650m1-b 电池为实验对象，对搭建好的电热耦合模型进行实验验证。实验分为恒流条件和动态电流条件。

3.1 恒流条件下验证实验

对于恒定电流条件，选择0.5 C，1 C，2 C 恒定电流对电池进行放电实验，将实验环境温度设置为25 ℃，记录电池在放电实验中的电压、温度变化过程，得到变化曲线，将所得数据和搭建的带滞回效应的电热耦合模型，以及未考虑滞回效应的二阶RC模型进行数据对比。图18 所示表示电池在环境温度为25 ℃时，不同放电恒定电流的电压变化和温度变化，其中实线为实验曲线，虚线为所模型预测曲线，点线为二阶RC 模型模拟曲线。

图18 25 ℃时不同放电恒定电流的温度与电压变化

图18 表明，模型预测温度与实验温度跟随性较好，随着放电时间而增加，模型预测的放电电压也与实验电压保持较高的跟随性。对于电池温度曲线，可以看出，在1 C 与2 C 放电电流的情况下，放电开始时，电池温度上升速度较为迅速，在0.5 C 放电情况下，温度上升较为缓慢，而0.5 C 的误差也较高于1 C 与2 C。随着电池温度的升高，电池与空气的温差会增大，热对流效果会增强，而温度上升速率则会降低，所以在中期，0.5 C 和1 C 温度会有一个平缓的上升，但当电池放电速率增加到2 C 时，由于电池内部产生的热量过大，这种平缓的温度上升并不存在。而放电结束时，极化电阻令电池大量发热，导致电池温度快速升高。对于电池电压变化，从图18(b)可看出，所搭建的模型相对于传统二阶RC 模型电压值更加贴近，拟合精度更高。综上所述，所建立的带滞回效应的电热耦合模型能够准确描述电池恒流条件下的情况。

3.2 动态电流条件下验证实验

由于恒流条件下无法模拟电动汽车真实运行情况，基于此，采用UDDS 动态工况实验获得电压电流曲线，利用MATLAB 搭建好的模型，将辨识出来的参数以及工况电流代入，仿真得出对应曲线与实验值进行对比，从而验证所建立带滞回效应的电热耦合模型能否较为真实反映电池工作情况。为了提升实验的说服力，再与同工况下二阶RC 模型的电压值与误差值进行比较。

UDDS 是用于轻型车辆测试的城市驾驶条件下特定测试方案。对于动态实验，实验分为以下三步:①将充满电的电池在试验温度下浸泡至少2 小时，以确保整个电池温度均匀。②使用1 C 的恒定电流对电池进行放电，放电时间足以耗尽大约10%的容量(有助于确保在动态充电部分避免过电压情况)③在合适的SOC 范围内执行UDDS 工况方案，合理性上选择从90%SOC 到10%SOC。最后在不同温度下重复进行实验，得到相应的数据。UDDS 工况电流如图19 所示，图19(b)为工况电流放大图。

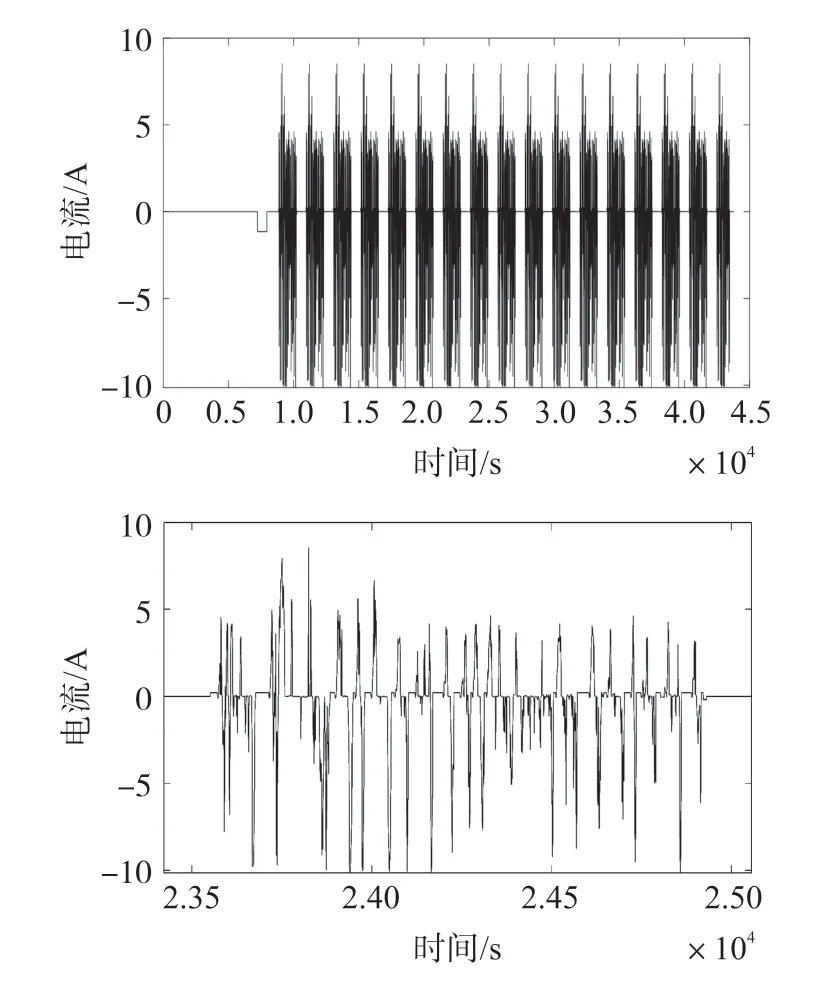
图19 UDDS 工况电流(上图为整体电流，下图为放大后部分电流)

由于UDDS 工况电流具有变化幅度不固定的特点，在模拟时锂电池的滞回效应将会更加明显，更能反映出电动汽车在运行时电池的工作状态。图20与图21 分别为15 ℃和25 ℃时，UDDS 工况下测量的电池电压以及曲线误差对比图，可以看出所搭建的带滞回效应的电热耦合模型的电压值与实际电压，虽然有一定程度的明显误差，但基本贴合，相对于传统的二阶RC 模型而言，精度更高，贴合度更好。从图20 和图21 的误差放大图可以看出，所搭建模型误差更小。

图20 15 ℃，UDDS 工况实验得出的电压曲线(上图为总图，下图为误差图)

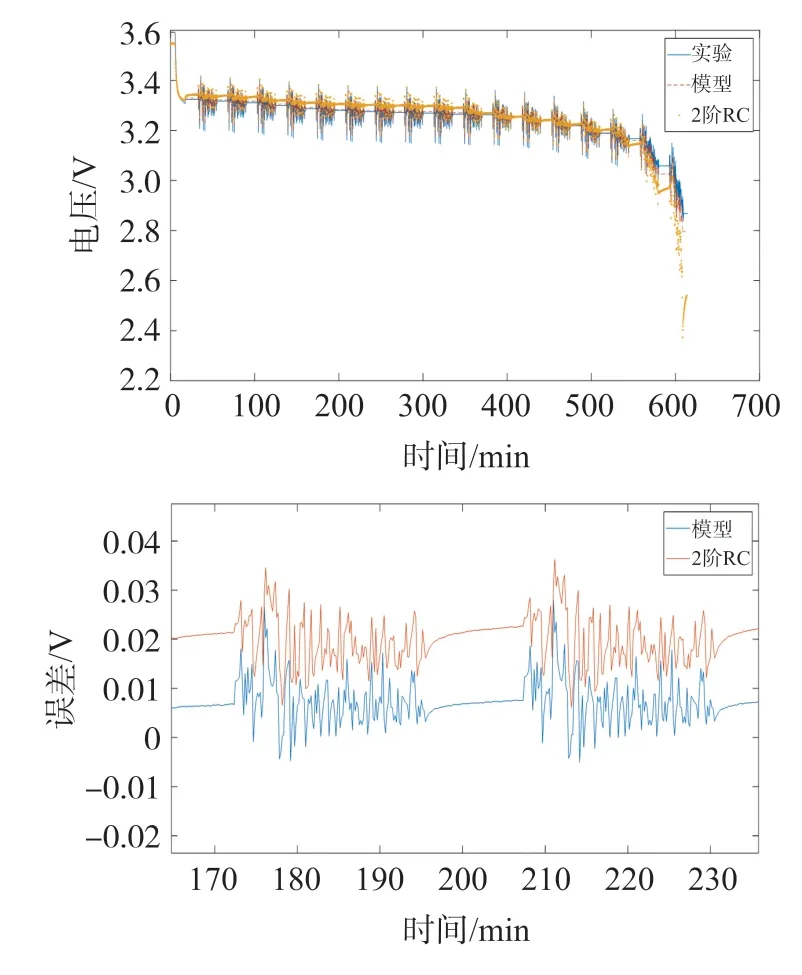
图21 25 ℃，UDDS 工况实验得出的电压曲线(上图为总图，下图为误差图)

在UDDS 工况下，由于电池的工作状态不断发生改变，所产生的滞回效应也较为明显，而文章所搭建的带滞回效应的电热耦合模型能够很好地处理这种现象，相较于以往未考虑滞回效应的电池模型，更好地跟随锂离子电池在工况过程中的电压值，提高了对锂离子电池的模拟精度。综上所述，考虑滞回效应电热耦合模型的误差在10 mV 左右，比传统二阶RC 模型精度提高了约0.013 V，在不同温度下，所搭模型的误差仍旧保持较小水平，模型精度很高。

4 结论

由于传统的电池模型忽略了电池滞回效应以及温度对模型精确度所带来的影响，文章提出了一种考虑滞回效应的电热耦合等效模型，根据实验得出数据分析了所建立模型的可靠性。通过MATLAB参数优化工具箱得出了滞回电压，利用查表法简化了等效电路模型计算复杂度以及仿真速度，将电模型与建立的二态热模型耦合，得到电热耦合模型，在此基础上，通过不同恒流和动态工况实验，对所建立的模型进行验证。

相对于以往的电池模型，本文提出的考虑滞回效应的电热耦合模型更契合锂离子电池在不同使用情况下的工作特性，能够更好地反映不同情况下电池的工作状态，有着较为出色的鲁棒性。仿真及实验结果表明本文所搭模型的误差在10 mV 左右，比传统二阶RC 模型精度提高了约0.013 V，在不同温度下，所搭模型的误差仍旧保持较小水平，模型精度很高。