基于改进PSO-BP 神经网络算法的半导体材料带隙宽度预测

肖 斌胡国梁

(西南石油大学计算机科学学院，四川 成都 610500)

半导体材料是导电性介于导体与绝缘体之间的材料。半导体材料因其“光生电”“热生电”等独特性质，被广泛地应用于电子通讯、航空航天、国防科研等领域。半导体材料的带隙宽度是影响半导体材料性能的重要属性之一。快速准确地模拟计算、预测带隙宽度对半导体材料的研究具有重要意义。在材料性能模拟计算领域，目前应用最为广泛的是基于复杂多电子波函数的密度泛函理论。然而密度泛函理论的计算需要花费大量时间，且在复杂环境下的模拟计算结果往往不尽人意。科学家们渴望一种更加快速、更加精确的材料性能模拟计算方法。随着信息时代的到来，材料科学领域产生的大数据为机器学习在材料性能模拟计算领域的应用提供了可能性[1]。从已有的材料科学领域大数据中进行数据挖掘，提炼出其中的数学规律来预测未知的材料性能是一种新型的材料性能模拟计算手段[2]。

最近几年一些通过机器学习预测半导体材料带隙宽度的探索取得了一定的进展。例如徐永林等人[3]使用套索算法(Least Absolute Shrinkage and Selection Operator，LASSO)、支持向量回归算法(Support Vector Regression，SVR)、梯度提升决策树算法(Gradient Boosting Decision Tree，GBDT)的融合算法找到了金刚石化合物带隙宽度与其相关特征之间的映射关系，开发了一种有效的带隙预测模型。Gu等人[4]将 SVR 和前馈神经网络算法(Back Propagation Neural Network，BP 神经网络)结合，提高了BP 神经网络性能的同时预测了56 种化合物的带隙宽度。Li 等人[5]通过偏最小二乘法构建纳米金属氧化物带隙值与结构参数的关系模型，预测不同晶型、不同粒径纳米金属氧化物的带隙值。郑伟达等人[6]通过随机森林算法可以有效地预测钙钛矿材料带隙性能。这些创新的工作展现了机器学习在材料带隙宽度预测上的应用。然而如何优化输入变量、降低预测模型的冗余仍是一个亟待解决的问题[7]。

本文建立一套基于统计学方法和改进粒子群优化前馈(PSO-BP)神经网络算法的半导体材料带隙宽度预测模型。该模型运用了统计学和机器学习的方法，从已知半导体材料数据集中提取9 种影响材料带隙宽度预测的重要特征属性，挖掘了这些重要特征属性与带隙宽度之间隐含的数学规律并将这种数学规律推广到带隙宽度的预测之中，从而提高了带隙宽度预测的效率。对照实验的结果表明，本文提出的预测模型均方误差相比对照模型降低了约25%，可靠性达到了75.15%，能更加有效地预测未知半导体材料的带隙宽度。

1 研究方法

1.1 数据集来源与描述

本文所用半导体材料带隙宽度实验数据源于徐永林等人[3]通过搜集整理、组分替换及理论计算等方式得到的443 种类金刚石结构材料体系的带隙宽度。该数据集包括晶体结构参数、阴阳离子的相对电负性差值、阴离子平均键长、所含元素族信息等42 种特征属性，以及1 种目标变量GAP(带隙宽度)。由于并非每种化合物都包含所有族的元素，因此数据集中部分特征属性出现大量的缺失值。为了保证算法模型的判断力及提高算法模型的泛化能力，删除了存在缺失值的特征属性，仅保留“A(晶格常数A)、B(晶格常数B)、C(晶格常数C)、BE(轴角β)、GA(轴角γ)、ED(阴阳离子相对电负性差)、NNCN(阴离子最近邻配位数)、V(方差)、ASBL(阴离子平均键长)、AAM(阴离子原子质量)、CAAM(阳离子平均原子质量)、AVEN(平均价电子数)、ETN(元素种类数)、6＿AIE(6A 组元素的电离能)、6＿AAM(6A 组元素的原子质量)、6＿AE(6A 组元素的电负性)”共计16 个特征属性。

1.2 输入变量的分析和选择

本文在数据集总体大小有限的情况下，绘制相关性系数图谱和方差表，以分析识别出高价值特征属性，尽可能降低数据集维度，缩短样本在数据空间上的距离，以降低预测算法过拟合的风险[8]。同时还要尽可能保留方差较大的特征属性，以保留数据集中隐含的信息，优化该算法的泛化能力。为此本文使用Pearson 相关系数和方差两种统计量来描述特征属性的重要程度。

Pearson 相关系数是一种描述两个变量之间的线性关系并将这种关系数值化的方法[9]。Pearson相关系数的值介于－1 与1 之间。Pearson 相关系数的绝对值越接近于1，表明两个变量之间的线性关系越强；Pearson 相关系数的绝对值越接近于0，表明两个变量之间的线性关系越弱。如果随着一个变量增大，另一个变量逐渐减小，则表明它们之间是线性负相关的，Pearson 相关系数小于0；如果随着一个变量增大，另一个变量也随之增大，则表明它们之间是线性正相关的，Pearson 相关系数大于0。具体公式如下:

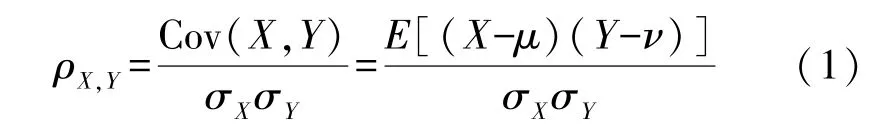
式中:Cov(X，Y)为随机变量X和Y的协方差，E为数学期望，μ和ν分别为随机变量X和Y的总体均值，σX和σY分别为随机变量X和Y的标准差。

采用方差评估单一特征属性的离散程度时，单一特征属性的方差越大，算法模型越容易分辨出其中的区别。具体公式如下:

式中:μ为随机变量X的总体均值，N为总体例数。

1.3 回归算法

1.3.1 基于集成学习和Adam 自适应矩估计法改进的PSO-BP 神经网络算法

本文提出一种基于集成学习和Adam 自适应矩估计法改进的PSO-BP 神经网络算法(以下简记为IPSO-BPNN)。该算法主要分为两个部分，一是基于集成学习改进的PSO 算法部分和二是基于Adam自适应矩估计法改进的BP 神经网络算法部分。

在PSO 算法部分采用了集成学习的思想进行改进。其具体方法为:第一步，随机抽取PSO-BP 神经网络训练集中20%的样本作为集成学习粒子群优化算法的训练集。第二步，无重复选取1 个集成学习粒子群优化算法的训练样本与PSO 算法构成1个弱学习器。随机抽取60%除该训练样本以外的训练样本作为该弱学习器的测试集。第三步，当集成学习粒子群优化算法的训练集中的训练样本全部取完时，利用弱学习器对应的测试集对所有弱学习器得到的神经网络权重值和阈值进行测试，选取误差最小者作为全局BP 神经网络的最优权重值和阈值。第四步，开始BP 神经网络的训练。

基于集成学习改进的优势在于在不遍历所有训练样本的前提下，尽可能重现原样本空间的数值特点，得到最佳BP 神经网络权重、阈值的估计。避免由于PSO 算法易早熟的特性导致PSO 算法优化结果远离BP 神经网络全局误差的最小值点。同时也避免了PSO 算法遍历训练数据集导致的训练时间大幅增加。

在BP 神经网络算法部分采用了Adam 自适应矩估计法作为BP 神经网络算法的优化器。Adam自适应矩估计法利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam 自适应矩估计的特点是其在经过偏置校正后，每次迭代学习率都有个确定范围，使得参数比较平稳，不易陷入局部极小值点。其公式如下:

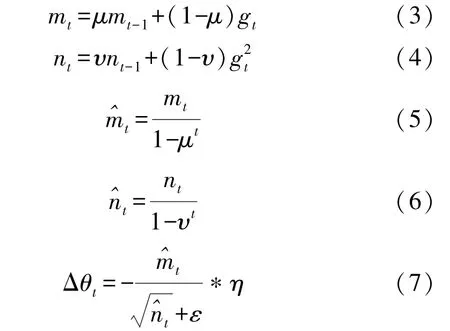
式中:gt是目标函数关于参数的梯度，mt、nt分别是对梯度的一阶矩估计和二阶矩估计。mt－1、nt－1是梯度的累计一阶矩估计、二阶矩估计，二者初始值皆为0。、是对mt、nt的校正。β1、β2分别是一阶矩估计和二阶矩估计对应的衰减速率，一般取0.9 和0.999，α是学习率，ε是防止出现除零错误的较小常数，一般取10－8。Δθt是根据、计算的动态学习率范围。

Adam 自适应矩估计法能够自动为各个参数分配学习率，训练末期不易摆动，整个训练期参数变化较为平稳。相比于随机梯度下降法，Adam 自适应矩估计法更适合优化非平稳目标，更不容易陷入局部极小值。

本算法的时间复杂度为O(m2＋mn2)，其中m正比于训练集样本数量，n正比于BP 神经网络中神经元数量。

1.3.2 对照模型的回归算法

本文使用LASSO[10]、SVR[11]、GBDT[12]以及未经改进的PSO-BP 神经网络算法(Particle Swarm Optimization-Back Propagation Neural Network，PSOBPNN)作为对照实验的回归算法。其中，LASSO 算法是在传统最小二乘估计上改良而来的一种多元线性回归算法；SVR 算法是支持向量机在回归问题上的一种应用；GBDT 是一种迭代的决策树算法。3 种算法均为回归问题常用的算法。

对照实验结果的表格引用了Ensemble 算法实验结果。Ensemble 算法是徐永林等[3]提出的一种有利于找到带隙宽度特征描述符的融合算法。它通过集成LASSO、SVR、GBDT 分别构成的弱学习器对数据集进行预处理，然后再次利用GBDT 构成的强学习器进行回归计算。

1.4 评价指标

对于1.3 节中不同回归模型产生的结果，本文使用平均绝对误差(MAE)、均方误差(MSE)、决定系数[13](R2)共3 种不同的性能评价指标描述了各个模型在测试集上的性能表现。MAE 和MSE 反映的是回归偏差的大小，其值越接近于0，说明该模型回归偏差越小，回归性能越好；R2反映的是回归结果的可靠性高低，其值越接近于1，说明该模型回归结果的可靠性越高。3 种评价指标的计算规则为如下:

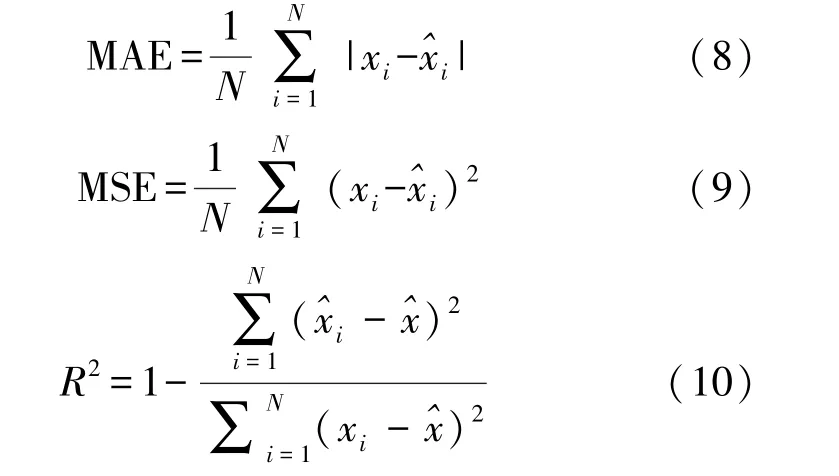
式中:N为样本总量，xi为测试集中对应的第i个实际值，为其对应的模型预测值，为测试集中所有实际值的平均值。

2 实验结果及分析

2.1 基于Pearson 相关系数及方差的输入变量选择

利用上述Pearson 相关系数公式可绘制数据集中特征属性之间、特征属性与带隙值之间的相关系数图谱[14]如图1。

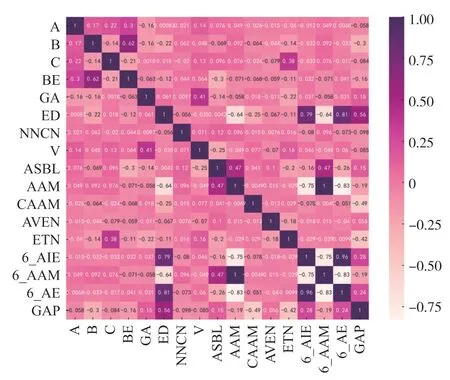
图1 数据集中特征属性之间Pearson 相关系数图谱

表1 描述了数据集中16 个特征属性的方差值。

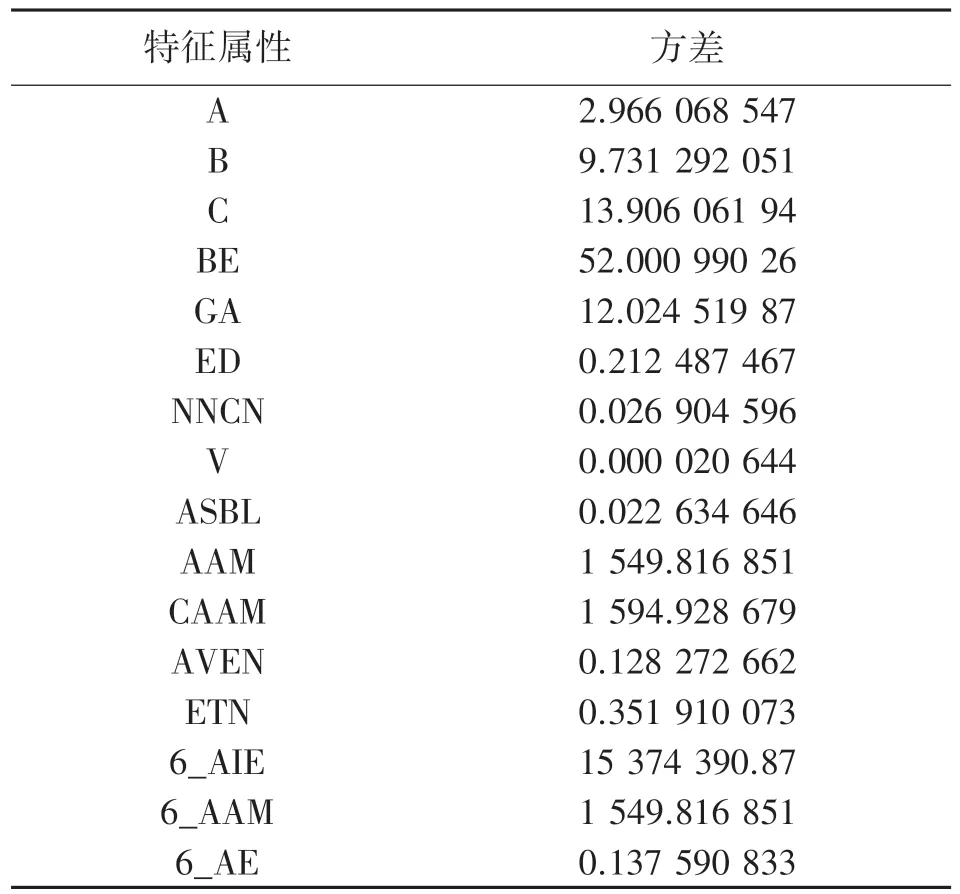
表1 特征属性的方差表

通过图1 可以发现6＿AIM、6＿AE、ED、ETN 四种特征属性之间存在多重共线性，因此只保留方差最大的6＿AIM。NNCN、V、AVEN 三种特征属性与带隙值之间的Pearson 相关系数较低，线性关系较差，因此予以删除。ASBL 的方差较低，且与AAM 存在一定的二重共线性，因此予以删除。

综上，本文在经过基于Pearson 相关系数和方差的输入变量分析与选择后，仅保留A、B、C、BE、GA、AAM、CAAM、6＿AIE、6＿AAM 共9 种特征属性。

2.2 对照实验的参数设定与结果

在对照实验中，IPSO-BPNN 与PSO-BPNN、Lasso、SVR、GBDT 一同在材料带隙宽度数据集上进行回归计算。各算法的输入变量均为上节中所述影响材料带隙宽度预测的9 种特征属性。

其中IPSO-BPNN 与PSO-BPNN 采用3 层BP神经网络结构。基于上述对输入变量的分析与选择，输入层神经元数量确定为9。以材料带隙宽度值数据为输出层，故输出层神经元数为1。隐含层节点采用ReLU 函数激活函数[15]。隐含层神经元个数由下列经验式计算并初步测试后确定为13:

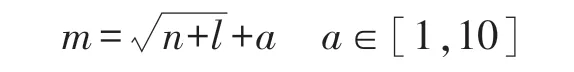
式中:m为隐含层神经元个数；n为输入层神经元个数；l为输出层神经元个数；a为1 至10 之间的整数。

在PSO 优化算法设置中，惯性权重w取0.8，加速因子c1＝c2＝2，r1、r2为(0，1)之间的随机数，粒子初始位置及速度均为随机值，迭代最大次数取50，设置粒子位置区间以防止出现权重、阈值过大的情况，但不设粒子速度区间。

在LASSO 算法中，正则项系数α值设为0.06，最大迭代次数设为1 000。

在SVR 算法中，核函数Kernel 设为径向基函数(Radial Basis Function，RBF)，核函数系数γ值设为10，错误项惩罚系数C值设为5，模型错误分类容忍度ε值设为0.01。

在GBDT 算法中，回归树个数设为1 500，学习率设为0.03，子采样值设为0.6。

在训练集上分别对PSO-BPNN 和IPSO-BPNN进行调优后，将测试集数据代入模型中输出预测结果并与实际值进行比较。

图2 所示为5 种算法预测结果的散点图。图中横坐标为带隙理论值，纵坐标为算法预测值。散点越接近于斜率为1 的黑线，预测效果越好。表2 是各个模型在材料带隙宽度数据集上的预测结果。

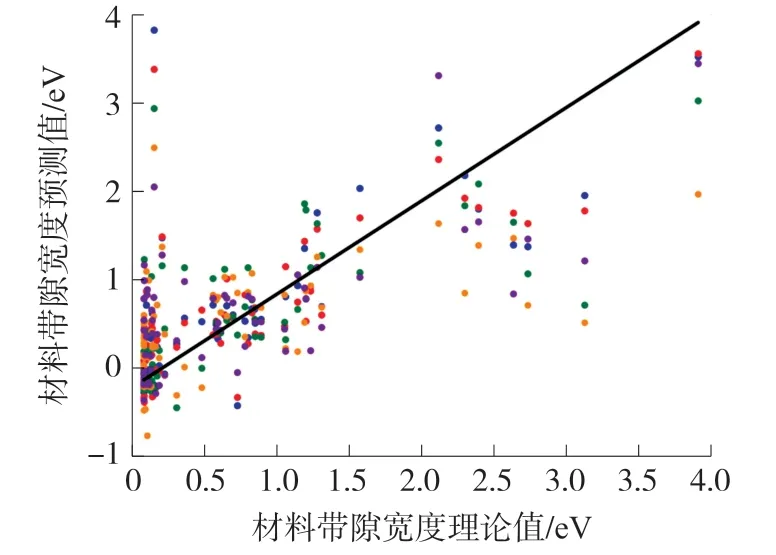
图2 5 种算法预测结果的散点图

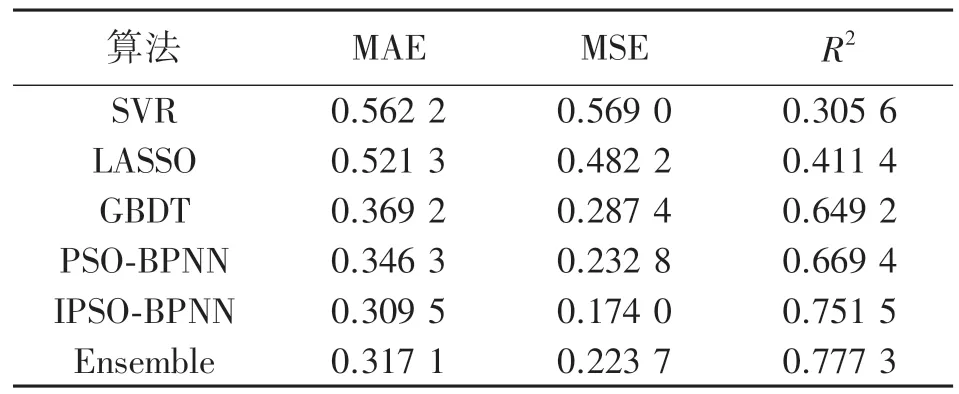
表2 各个算法在材料带隙宽度数据集上的预测结果

由图表可见IPSO-BPNN、PSO-BPNN、GBDT 具有较好的预测效果。而IPSO-BPNN 预测值相比于其余4 种算法都更加接近真实值，其MAE、MSE 均为5 种算法中最低，分别达到了0.309 5 和0.174 0，相比次好算法降低了约11%和25%。R2值为5 种算法中最高，达到了0.751 5。得益于优化的回归算法，IPSO-BPNN 具有更好的预测效果。

IPSO-BPNN 相比于引用的Ensemble 算法来说各有胜负，MAE 相差无几，MSE 占据优势，R2略有不足。IPSO-BPNN 略微牺牲了R2值换得了更小的预测误差。

此外，5 种算法均对于0～0.2 eV 之间的材料带隙预测效果较差，其原因可能是该段用于训练的数据集较少，使得5 种算法没能很好学习到该段数据的特点，其次带隙宽度为0～0.2 eV 之间的材料性质接近于导体，与典型的半导体之间存在着差距，致使5 种算法未能很好地分辨其中的区别。

3 结论

本文设计了一种基于统计学方法和机器学习的半导体材料带隙宽度预测模型，并针对于类金刚石材料带隙宽度数据集进行了预测实验。通过输入变量的分析与选择、PSO-BP 神经网络算法的优化等手段，使得本预测模型预测的均方误差低至0.174 0，决定系数提升至0.751 5，相比于对照算法更具准确性。本预测模型在材料带隙宽度上的预测精度能够更好地满足研究实际需求，对提高预测材料带隙宽度的效率具有重要的应用价值。而本算法的时间复杂度较高，实际运行速度较PSO-BPNN 算法更慢。下一步的工作将降低算法的时间复杂度，使得本算法在材料带隙宽度预测方面取得更加令人满意的效果。