反应堆压力容器在严重事故条件下的断裂力学评价
王大胜,周 强,毛剑峰
(1.深圳中广核工程设计有限公司,广东深圳 518124;2.浙江工业大学 化工机械设计研究所,杭州 310023)
0 引言
在堆芯熔毁的严重事故(SA)中,先进的核电站(NPP)广泛采用 “容器内滞留(IVR)”策略来维持反应堆压力容器(RPV)的安全[1]。事实上,自1996年以来,美国核管理委员会(NRC)已将IVR措施认证为SA管理的标准措施。在大多数情况下,IVR措施是在RPV的外壁上提供长期的水冷却,因此在SA期间无需任何人为行动,就可以去除衰变热。IVR措施实施过程中,外部水冷却是事故管理的最重要特征,如图1[2]所示。在IVR的传统概念中,RPV的下封头(LH)在堆芯碎片到达内部之前完全淹没在水浸中[3]。因此,在RPV内形成的熔池温度约为1 327 ℃,而容器外壁的温度接近150 ℃[4]。根据事故期间RPV临界热流(CHF)的基本假设,可以从先前的研究中得知,RPV的安全性可以在规定的时间内得到保证[5-7]。在2011年日本福岛核事故之前,上述常规IVR概念并未受到严重挑战。但是,当冷却水突然注入后,RPV结构内外温差急剧增大,加上热冲击作用,RPV外表面产生了多处裂纹,如图2,3[8]所示,事故后果表明,按照无裂纹RPV结构的安全评估结果受到了严重的挑战[9]。实际上,标准事故设计中没有考虑带裂纹的RPV结构,因而类似福岛核事故完全超出了传统事故条件下的设计和安全评估范围。因此,在严重事故条件的72 h内,有裂纹的RPV能否保持压力边界的完整性是防止核泄漏的关键问题之一。
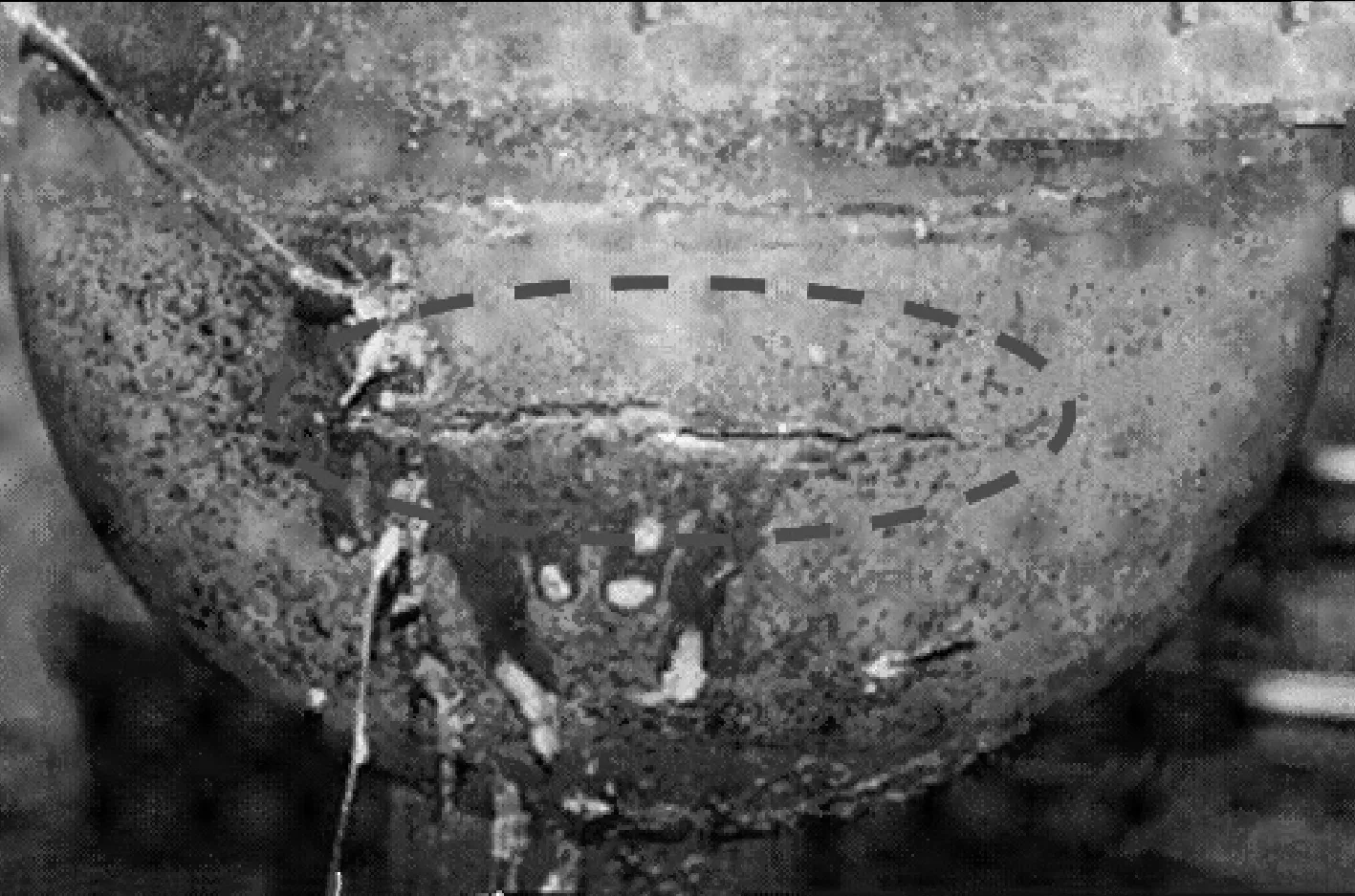
图2 失效后的反应堆压力容器Fig.2 The surface of failed RPV
欧盟核电堆芯熔毁试验项目(EC-FOREVER)测试提供了丰富的数据源,部分验证了RPV的断裂模型和欧盟核电行业结构安全评估规范,其RPV破裂如图3所示。EC-FOREVER的项目总协调在德国罗森多夫进行,以WILLSCHÜTZ等[10]都对每项测试进行背靠背地模拟计算及分析,主要采用Ansys多物理耦合方法,建立2D的RPV结构对主要IVR测试项目进行了热-流-固耦合分析。国内MAO等[11]研究者利用非线性多物理场有限元法,计算分析了IVR条件下RPV的蠕变失效。KOUNDY等[12]指出,测量和计算的最大位移值都出现在失效破裂处,Ansys模拟预测的RPV破裂点与试验测量值非常一致。对于IVR下RPV结构分析,一般需要同时考虑热模块和结构模块的耦合计算,才能较好地预测RPV 失效模式、位置和时间。KULKARNI等[13]利用38 kW的恒定功率加热器对RPV进行堆芯熔融试验,容器内充入25 bar的氩气,发现RPV材料的初始熔化温度略小于焊缝熔化温度,利用数值方法分析了2D轴对称RPV失效破裂,发现裂纹水平沿壁厚法向分布,并分析了单个裂纹行为[14]。ABENDROTH等[15]计算分析了包括1/1(真实比例)和1/10(缩比模型)的3D裂纹尺寸及其位置变化对RPV破裂行为影响。本文给出RPV在严重事故条件下的断裂力学计算结果,包括与温度相关的应力(应变)分布。由于外壁温度低于蠕变温度范围,没有考虑蠕变影响,但是建立了含裂纹下封头的有限元模型,用于分析研究J积分、温度及应力变化规律。

图3 裂纹和蠕变孔隙破坏示意图Fig.3 The schematic diagram of creep porosity and crack
1 理论背景与建模
1.1 热应力体J积分的理论模型
为了简单起见,先给出适用于超弹性材料的下列公式。
(1)
(2)
式中,σij为热-机引起的势函数,表示应力张量;W为应变能密度;εij为应变张量。
实际上,上述公式也可用于塑性增量理论。在该理论中,禁止局部卸载,应力空间中的所有加载路径应保持径向,以便主应力的比率保持不变。塑性区应封闭在积分路径(或积分区域)内,并假设裂纹面没有载荷,也不存在体载荷。
为了说明3DJ积分,绘制了具有弯曲裂纹前缘的3D平面裂纹,如图4所示,图中定义了一个局部裂纹尖端坐标系,其中ξ1轴垂直于裂纹扩展方向上的裂纹前缘,而ξ2轴垂直于裂纹面,ξ3轴与裂纹前缘相切,s是局部裂纹前缘坐标。实际上,在计算3DJ积分时,通常使用两种典型的J积分公式,第一种是路径积分和面积积分的组合,即:
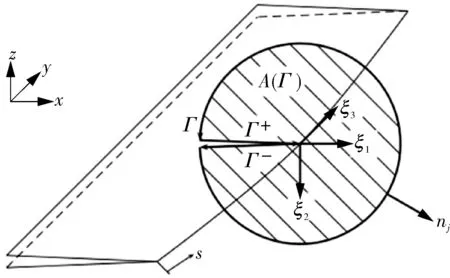
图4 3D积分路径/面积Fig.4 The 3D integral path/area
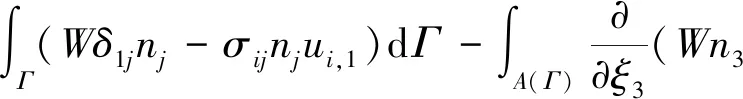
(3)
关于虚拟裂纹扩展(VCE)的另一个公式[16],采用qk的3D坐标函数和体积积分域来求解(见图5):
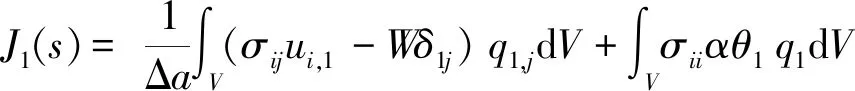
(4)
在上述两个方程中,指数i,j,k在坐标ξ1,ξ2,ξ3上变化。式(4)中,q1是ξ3和裂纹尖端径向距离(r,q2=q3=0)的函数,q1可表示为:
(5)
具体讲,积分域是具有长度δs和半径r0的圆柱形体积,如图5所示。由此产生的虚拟裂纹前缘扩展(VCFE)可描述为一个平面抛物线形区域,其大小可表示为:
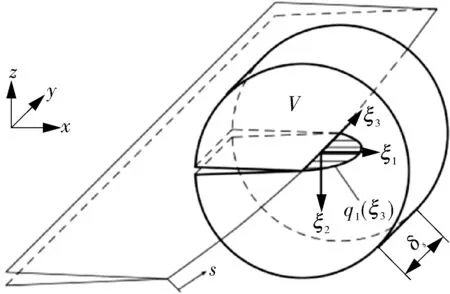
图5 具有弯曲裂纹前缘的3D积分体积Fig.5 The 3D integral volume of curved crack front edge
(6)
1.2 Ansys中的J积分计算策略
沿定义路径的积分算法早已实现,以2D面积积分为例,其近似为沿Γi的n个线积分之和,乘以环段wi的宽度,如图6所示。实际上,wi在这里被设置为一个常数,这在利用有限元网格计算时是有用的。可以看出,对裂纹尖端进行了加密细化,离裂纹尖端越远,宽度随之增加。Ansys中的积分计算策略认为[17],最内侧和最外侧积分环的宽度必须适合积分区域内最小和最大的有限元网格。
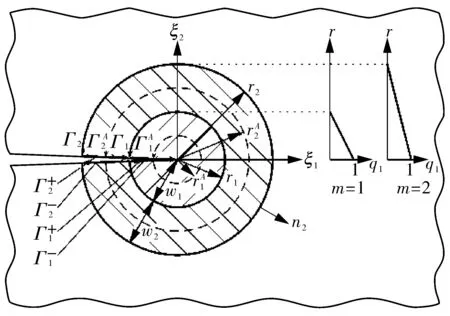
图6 Ansys中进行区域积分的不同积分路径Fig.6 The different integral paths of integral region in Ansys
(7)
(8)
(9)
(10)
(11)
(12)
在3D情况下,计算不同ξ位置的3个面积积分,乘以加权因子δsj,然后相加。沿ξ3的积分格式类似于一维高斯积分,位置ξj和权重δsj在式(11)(12)中表示。应注意圆柱形积分体积δs的深度,因为它们必须等于或小于沿裂纹前缘的单元尺寸。
1.3 含裂纹RPV有限元模型
本文重点研究RPV内熔融物滞留情况下的断裂力学行为。在有限元建模中,外部水冷效果由温度相关传热函数给出,在IVR启动注水后,RPV外部将被快速淹没,注水液面上升比较快,因此本文分析中假设RPV外表面被冷水淹没的情况。在临界热流密度下,从核状沸腾到膜状沸腾过渡,RPV的外表面最高温度约为150 ℃[9]。由于单元(Solid 182)不允许直接热-机耦合,因此必须执行顺序耦合,计算分解为预定义的时间步长,对于每个时间步,得到一个瞬态解,并且在随后的力学计算中采用空间温度场作为体载荷来计算热相关场,以及应力场,文献[18]证明以上有限元计算方案有利于结果收敛。为此,本文利用Ansys计算了3种不同内外径比(Ro/Ri=1.01,1.10,1.70)RPV上不同半椭圆裂纹排列结构下沿裂纹前缘的3DJ积分。
1.4 半椭圆表面裂纹的3D子模型
建立半椭圆形表面裂纹的3D子模型,位置和形式如图7所示。由于瞬态温度场由热计算求得,所以只需要得到力学解。这种方法在前面已描述,用于获得热机械解,并使用第1.2节中的3D积分模型和计算策略来计算沿3D裂纹前缘的J积分。图7示出了带有裂纹的RPV模拟中的边界和起始条件,3D轴对称模型在外侧的最大应力位置(也称为“焊缝”)处包含周向裂纹。对于边界条件,外表面温度为150 ℃,而RPV内熔体温度约为1 327 ℃,与临界热流条件相对应。
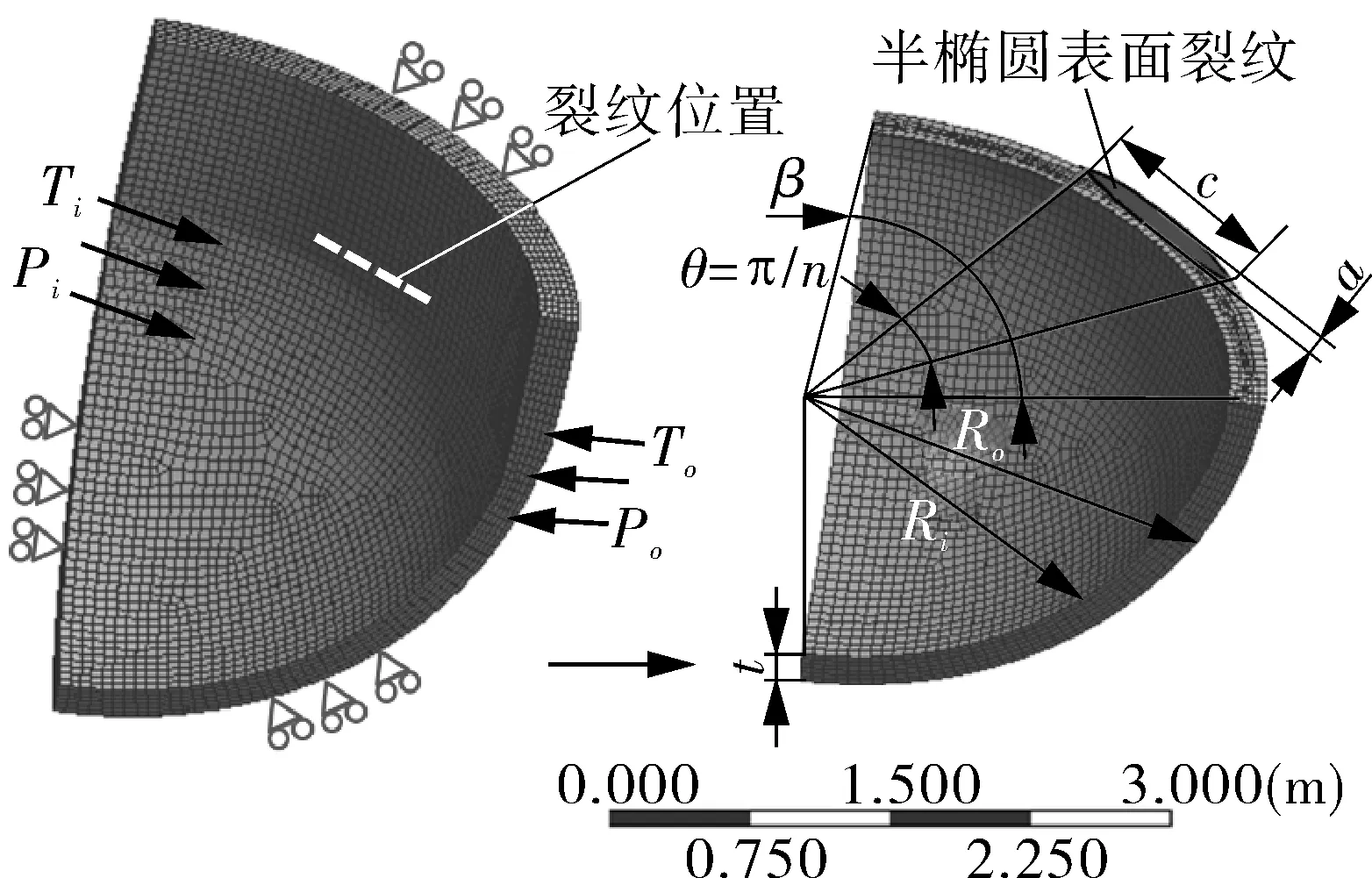
图7 RPV含裂纹的三维有限元模型Fig.7 The 3D finite element model of crack-containing RPV
1.5 裂纹的无量纲J积分及验证
当工作温度较大时,应考虑材料的延性,采用修正的弹性本构关系作为基准温度下延性断裂分析的基础。在韧性断裂模型中,损伤起始准则为最大主应力准则,演化规律以能量释放率为判据,弹塑性断裂力学(EPFM)分析采用指数软化模型。在平面应变条件下,能量释放率可由下式计算:
(13)
根据文献[19]给出的K00,所有的归一化应力强度因子(SIF)均进行归一化处理,薄、厚球形压力容器外表面产生的环向裂纹的SIF与裂纹深度的关系如下:
(14)

(15)
Q为椭圆裂纹的形状因子,由第二类完整椭圆积分的平方给出,通常近似[20]为:
(16)
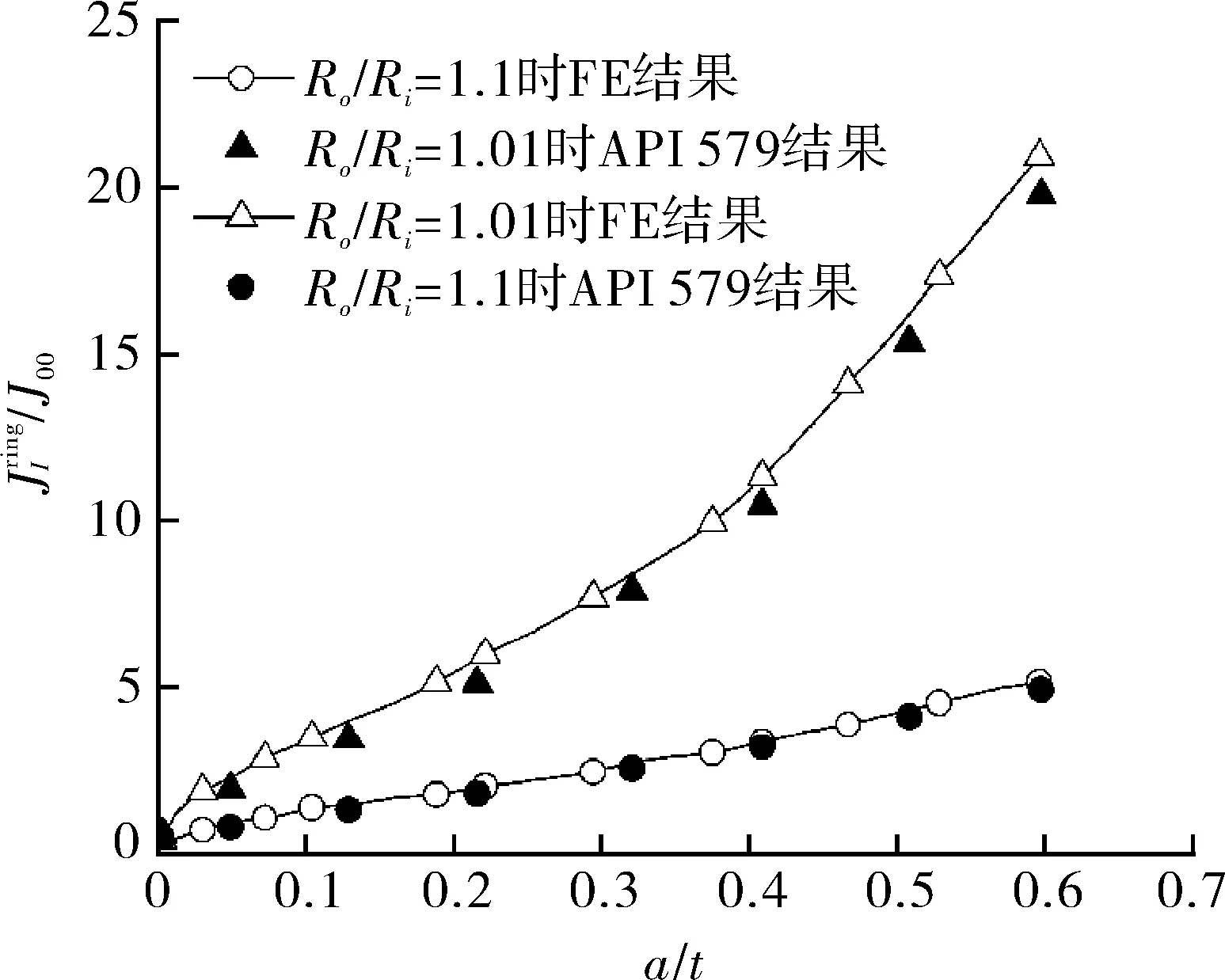
图8 有限元法和API 579标准中解的对比Fig.8 Comparison of J-integral solutions of finite element and API 579
由于几何构型的对称性不同,只对含裂纹的球形下封头进行了分析,赤道面ψ=0°和纵面ψ=90°如图9中定义。下封头内表面施加p=2.5 MPa压力,在裂纹张开面考虑内压的作用。为了适应裂纹前缘附近的奇异应力场,采用一层20节点等参块状单元折叠成楔状,在裂纹前缘形成奇异单元,并划分相应位置,顶部至少有4层网格。此外,模型的其余部分同时包含了20节点块状和10节点四面体单元。裂纹尖端附近的网格很小,网格密度随裂纹尖端距离的增大而增大,如图9所示。利用裂纹面位移外推法提取J积分,并将其计算方案以用户子程序构建在Ansys中。考虑到RPV上最可能的裂纹位置,假设所有裂纹在赤道面上是相同、等间距和共面的。在有限元计算中,考虑了具有不同a/c的最可能的半椭圆形裂纹,裂纹形式如图9所示。
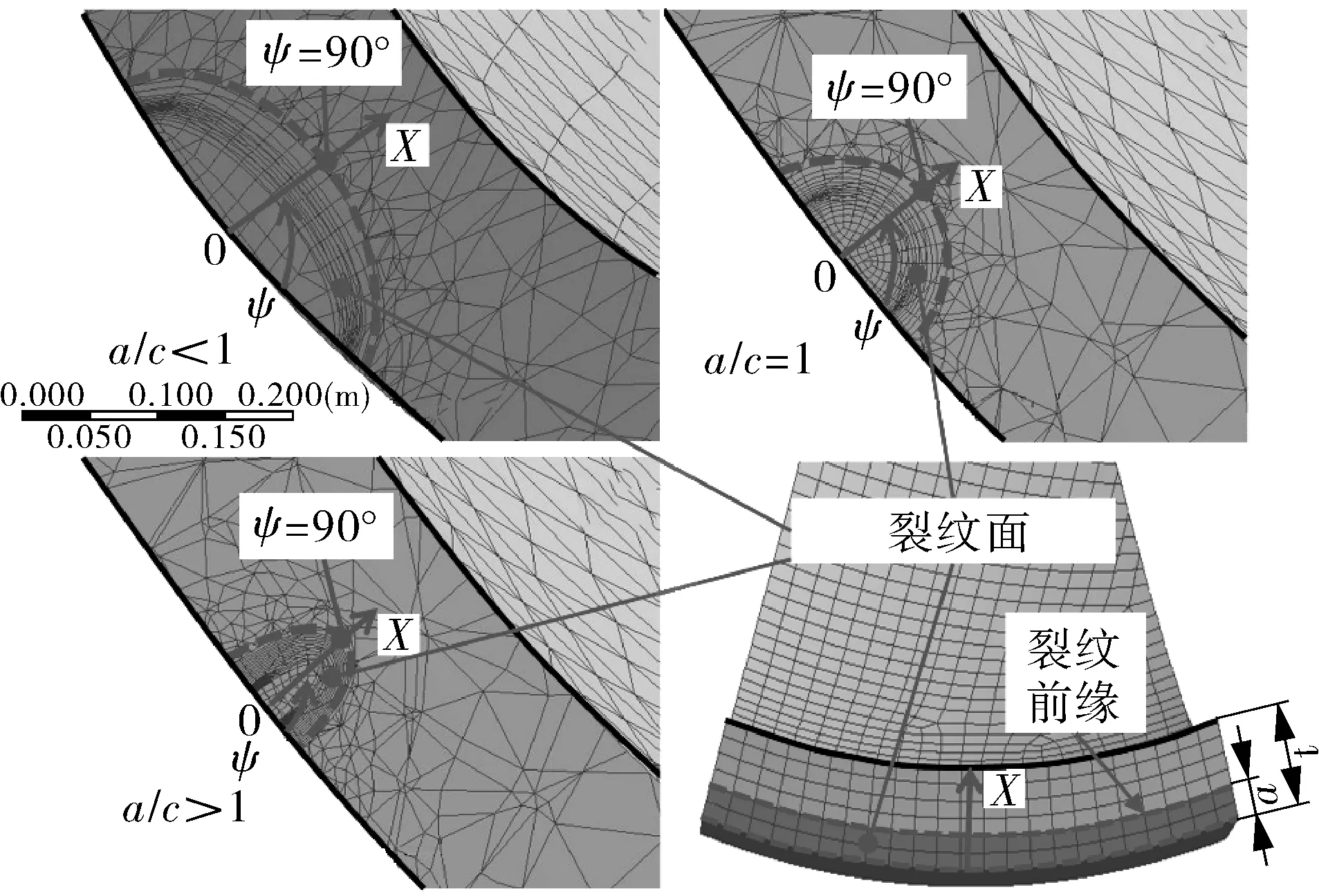
图9 不同椭圆度裂纹前缘区域的有限元网格Fig.9 The grids of crack front edges of different semi-elliptical cracks
2 结果与讨论
2.1 RPV场参数演化及分布
堆芯熔融严重事故条件下,冷却水最终淹没RPV,因为水注满整个堆腔的时间相对较短,本文不考虑水位上升的过程。图10示出了不同时间沿着壁厚路径A的温度分布,可以看出,内壁温度等于开始时的熔池温度,并且随着时间的增加而缓慢下降。实际上,在前几秒内,靠近内壁的温度有急剧下降的趋势,而随着时间的增加,整个壁厚仍存在较高的温度梯度。虽然72 h内的内壁温度略低于10 h时的内壁温度,但t≥1 h时沿壁厚温度分布已非常相近。
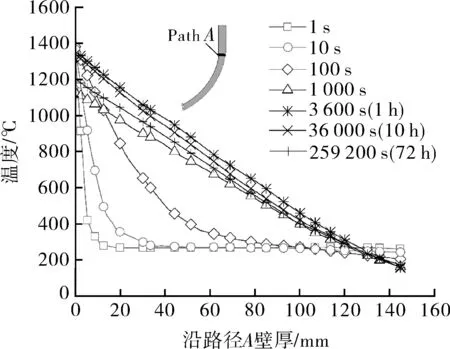
图10 不同时间下路径A沿壁厚的温度分布Fig.10 Temperature distribution of path A along wall thickness at different time
从RPV外表面(x=149 mm)上看,温度梯度实际上是随着时间的增加而上升的,在3 600 s(1 h)左右达到最大值。因此,该温度梯度导致容器外部出现较大的环向应力,如图11所示。
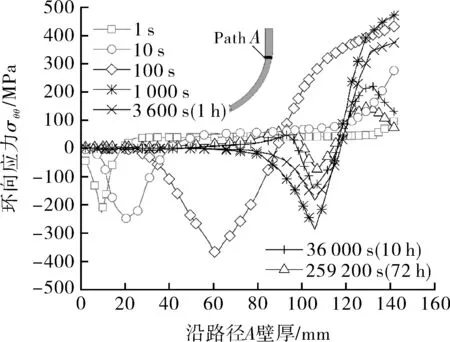
图11 不同时间路径A沿壁厚的应力分布情况Fig.11 Stress distribution of path A along wall thickness at different time
图11揭示了压缩状态应力朝着内壁表面减小,导致其应力承载能力减少,主要是因为熔融物接近或高于RPV材料熔点的高温作用。此外,最大应力出现在球形封头和圆柱段的过渡区,即焊缝位置,这个位置容易出现裂缝,也是最危险的地方。因此,假设半椭圆形裂纹出现在上述位置。
在传统的IVR概念中,RPV的内表面暴露于温度T>1 000 ℃的熔池中,而内压是通过多级泄压阀释放完全,因此只要RPV材料没有被熔穿,即不会发生所谓的“热失效”,堆芯的熔融物就被滞留在RPV内。但是实际的事故情况下存在内压和结构裂纹的影响,这时RPV的破裂风险急剧加大。图12示出在p=2.5 MPa内压下含半椭圆形裂纹RPV的应力场和温度场,由此可知,裂纹尖端处应力集中现象非常明显,已超过材料的屈服强度,在内压和热应力的作用下发生了整体膨胀和局部外凸,特别是含裂纹区域存在更大的应力和温度梯度。
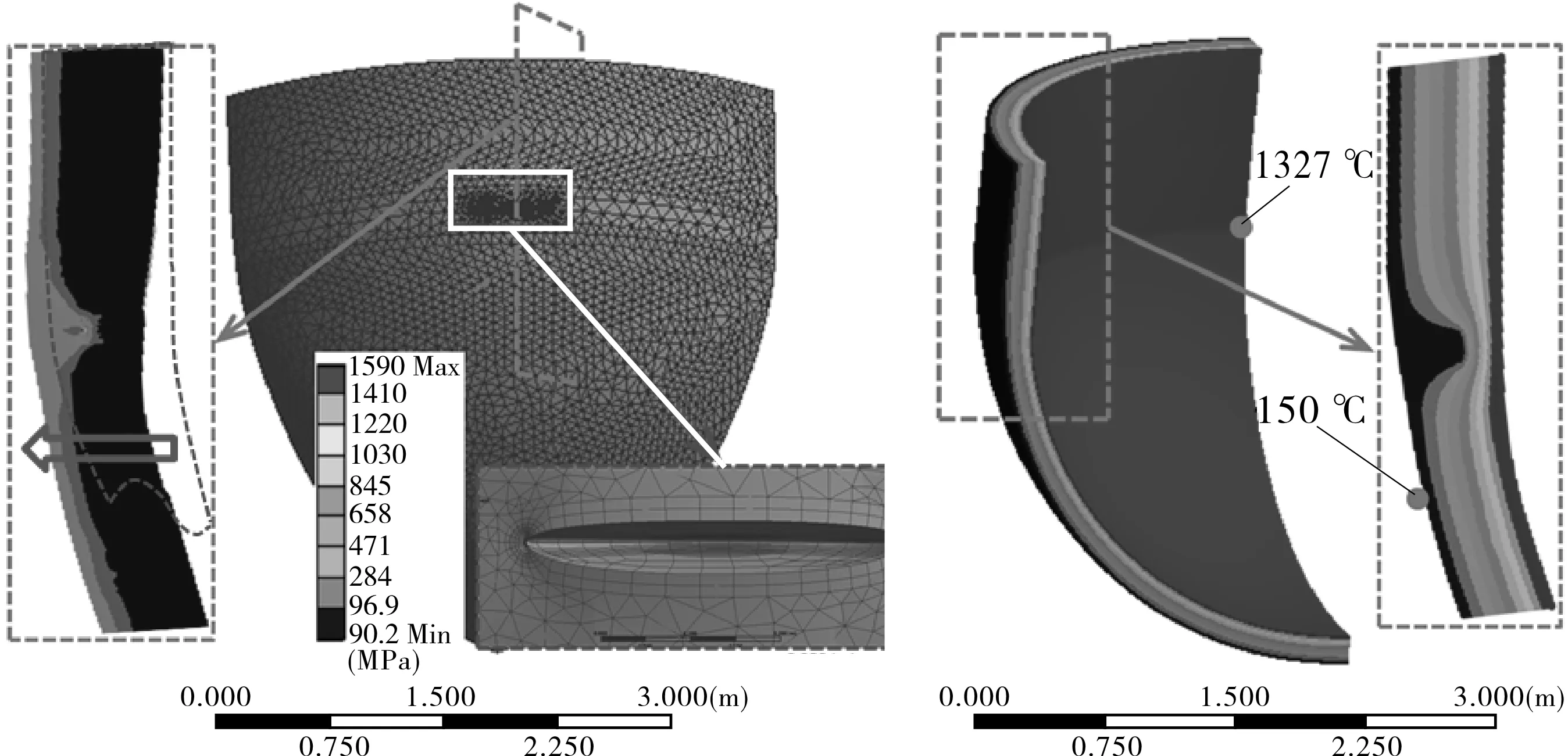
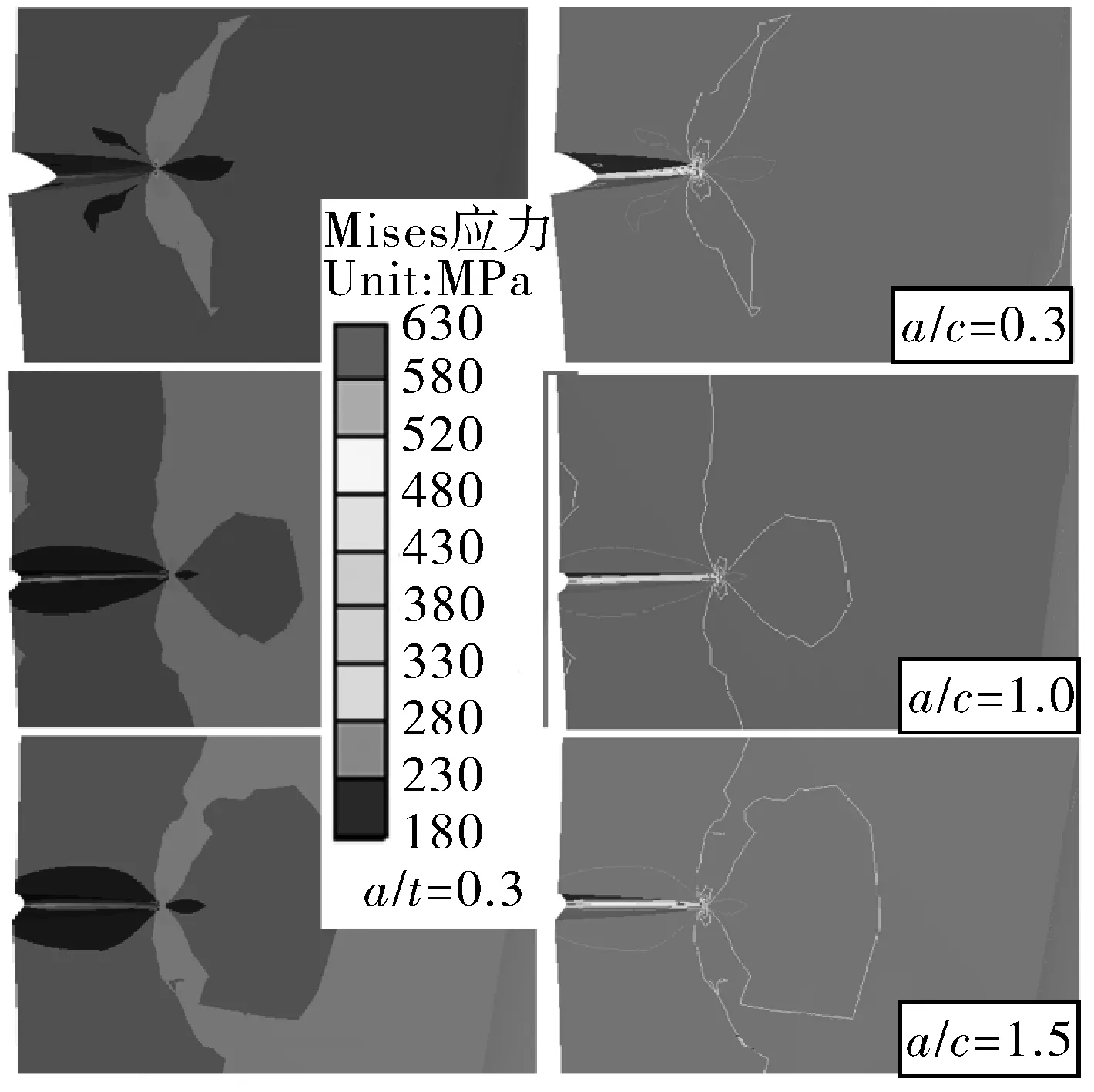
图12 半椭圆形裂纹周围的应力及温度分布Fig.12 Stress and temperature distribution around the semi-elliptical crack
图13(a)示出不同椭圆度裂纹(a/c=0.3,1.0,1.5)前缘周围的等效应力分布。结果表明,裂纹尖端的应力集中现象比较明显,但裂纹尖端的应力集中并不总是发生在裂纹最深处。实际上,图13描述的周向裂纹处于1/4对称RPV模型外侧应力最大处,应力最大值约680 MPa。从图13还可以看出,3种椭圆度裂纹的整体应力水平不一致,以裂纹最深处应力水平看,呈现a/c=0.3的应力水平大于a/c=1.0的,同时a/c=1.0的应力水平大于a/c=1.5的。从裂纹剖切面看,应力分布明显不对称,如图13(b)所示。值得注意的是,不同椭圆度裂纹最大应力处也不同,比如针对a/c=0.3椭圆度裂纹,最大应力处出现在靠近中间深度,而对于a/c=1.0,1.5的裂纹,最大应力处出现在靠近RPV外表面的裂纹尖端。不同椭圆度裂纹对应不同的裂纹前缘应力分布,a/c=1.0椭圆度对应的裂纹前缘应力较小,应力集中现象相对不明显,而a/c=0.3椭圆度的RPV出现最严重的应力集中现象。
(a)水平视角
2.2 裂纹参数对无量纲J积分的影响
为了确定不同参数对裂纹前缘J积分分布的影响,考虑了半椭圆裂纹的3种几何形式,椭圆度分别为a/c=0.3,1.0,1.5,不同裂纹深度a/t=0.05~0.55,以及不同裂纹密率阵列δ=0~0.9情况下的裂纹前缘J积分分布,分析评估了JI/Jo分布情况,其中Jo为a=15 mm情况下的J积分结果。
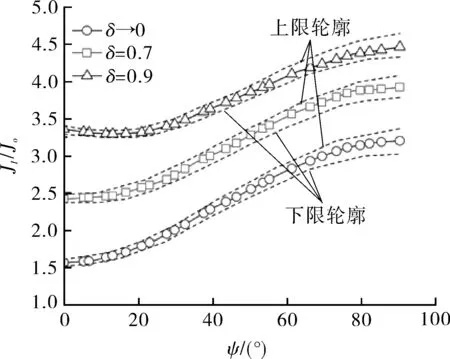
典型球形下封头Ro/Ri=1.1,当裂纹密率δ=0~0.9时,在相对浅裂纹a/t=0.3(见图14(a))和深裂纹a/t=0.6(见图14(b))前缘的J/Jo随参数角ψ的变化如图14所示。由图14(a)(b)的比较可以看出,沿裂纹前缘的JI/Jo分布具有不同的模式,a/t=0.3浅裂纹的J/Jo分布的模式与a/t=0.6深裂纹的几乎相反。对于浅裂纹情况,JI/Jo的最大值出现在ψ=90°的最深裂纹处,如图14(a)所示;而对于深裂纹情况,JI/Jo的最大值发生在尖端ψ=0°附近,如图14(b)所示。对于浅裂纹或深裂纹,沿整个裂纹前缘的JI/Jo值随裂纹密率δ的增加而增大。在共面周向裂纹中,沿整个裂纹前缘的JI/Jo随裂纹密率δ的增加而增大,反映了阵列裂纹的增加导致RPV承载力的下降,裂纹往前扩展加剧。相邻裂纹之间的主要相互作用发生在ψ=0°的尖端,从而导致JI/Jo梯度和Jmax增大。
(a)a/t=0.3
为了评估下封头裂纹密率对裂纹前缘最大J积分的影响,对a/c=0.3的椭圆度和Ro/Ri=1.1的几何形状,δ=0.9,0.7,0的3个共面裂纹阵列的Jmax/Jo与裂纹深度的关系分析如图15所示。尽管裂纹密率δ有所不同,但Jmax/Jo与a/t的之间关系趋势相似,如图15所示,随着δ的增大,Jmax/Jo随之增大。此外,随着裂纹深度a/t的增加,Jmax/Jo单调增加,Jmax/Jo与裂纹深度a/t呈分段线性关系。由图15可以看出,Jmax/Jo与a/t之间关系曲线可分为两个阶段,即初期快速增加和后期稳定增加。
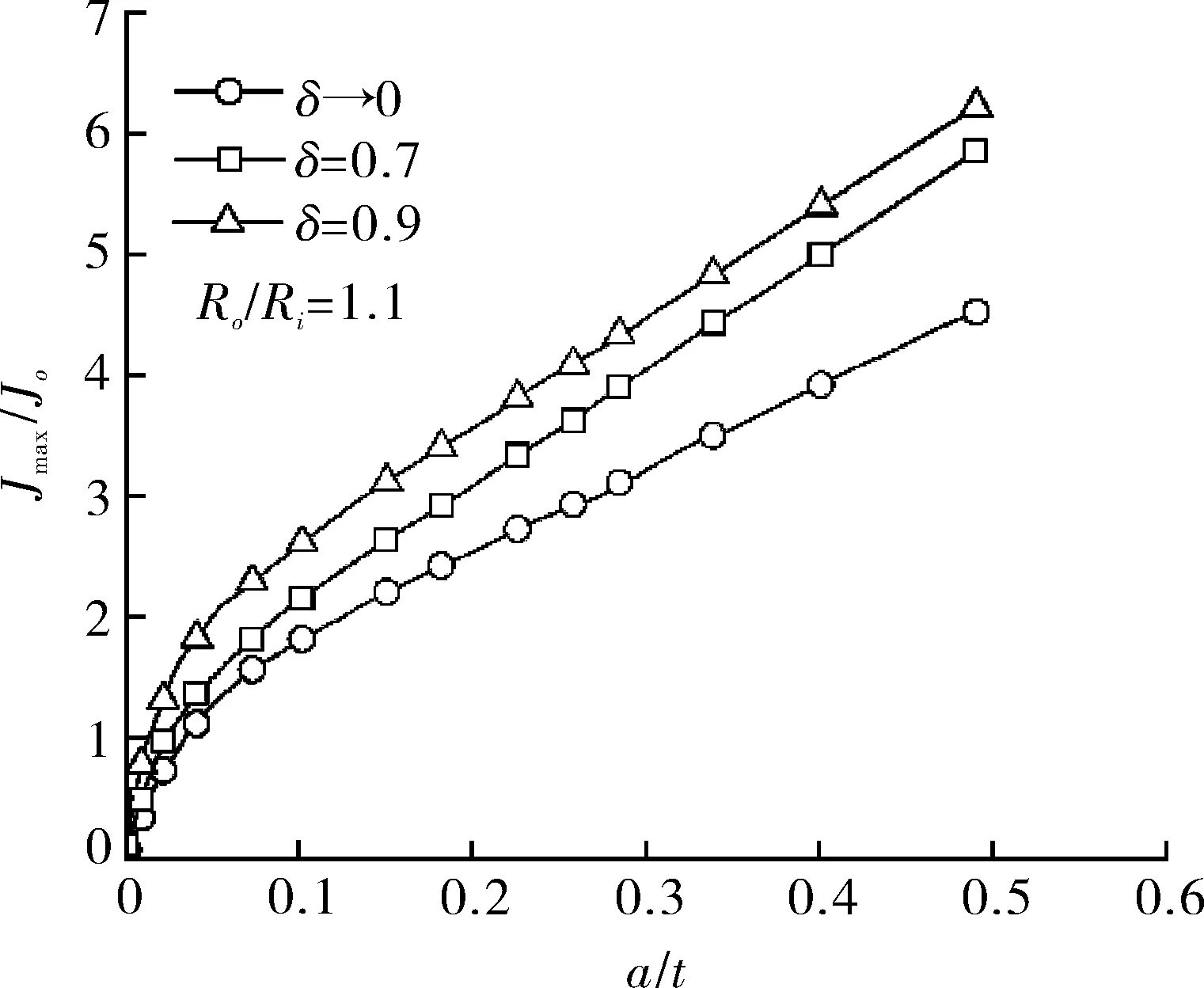
图15 椭圆度a/c=0.3下不同裂纹密率δ对Jmax/Jo变化影响Fig.15 Effect of crack density δ on Jmax/Jo for crack a/c=0.3
与椭圆度a/c=0.3裂纹J分布相比,a/c=1.0的裂纹最大JI的位置在尖端ψ=0°与裂纹最深点ψ=90°之间,并靠近ψ=0°的位置,JI随裂纹深度的增加而呈现不同分布,如图16所示。对于较浅裂纹和较深裂纹,JI值也随裂纹密率的增加而加快上升,沿整个裂纹前缘的JI/Jo分布随裂纹密率δ的增加而增大。在a/c=1.0的裂纹椭圆度下,a/t=0.3和a/t=0.6深度的JI/Jo沿裂纹前缘分布相似。由图16可以看出,当裂纹深度变大时,最大JI所在位置更接近最尖端点ψ=0°,而且最大JI值更高。与最大JI位置不同,对于浅裂纹和深裂纹,最小JI都出现于最内侧点ψ=90°(也称为“最深裂纹深度”)。JI/Jo随着裂纹深度a/t的增加而增加,但随着裂纹深度的增加,裂纹密率δ引起的JI/Jo数据的离散更为明显,如图16(b)所示。由图16(b)还可以看出,当a/t=0.6和δ=0.9时,最大JI是Jo的7.0倍,而a/t=0.6和δ=0时,最大JI是Jo的3.2倍。从图17可以看出,当裂纹形状接近圆形(a/c=1.0)时,裂纹密率δ对Jmax/Jo的影响非常敏感,而且影响也很大,随着裂纹深度a/t增加,Jmax/Jo单调增加。
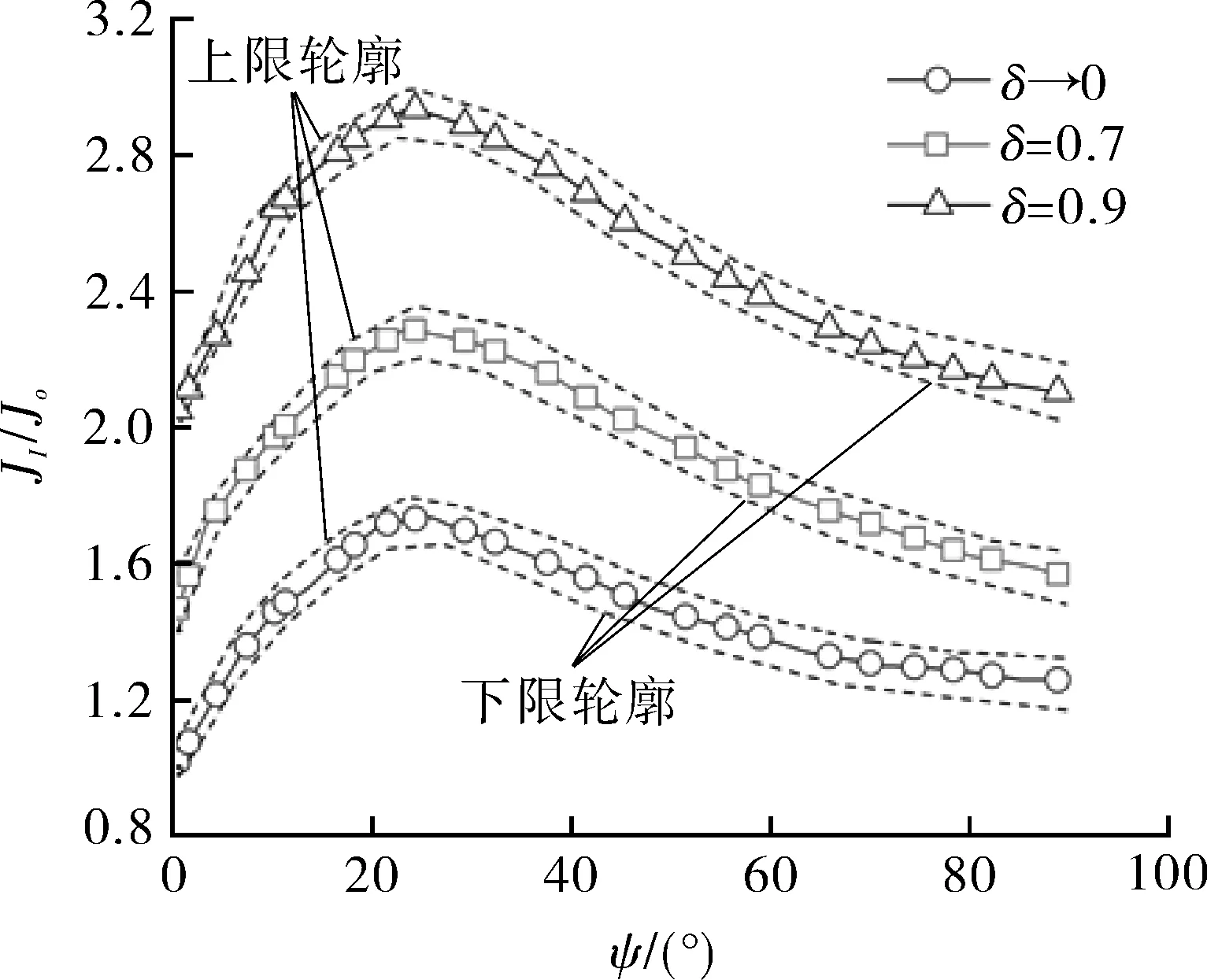
(a)a/t=0.3
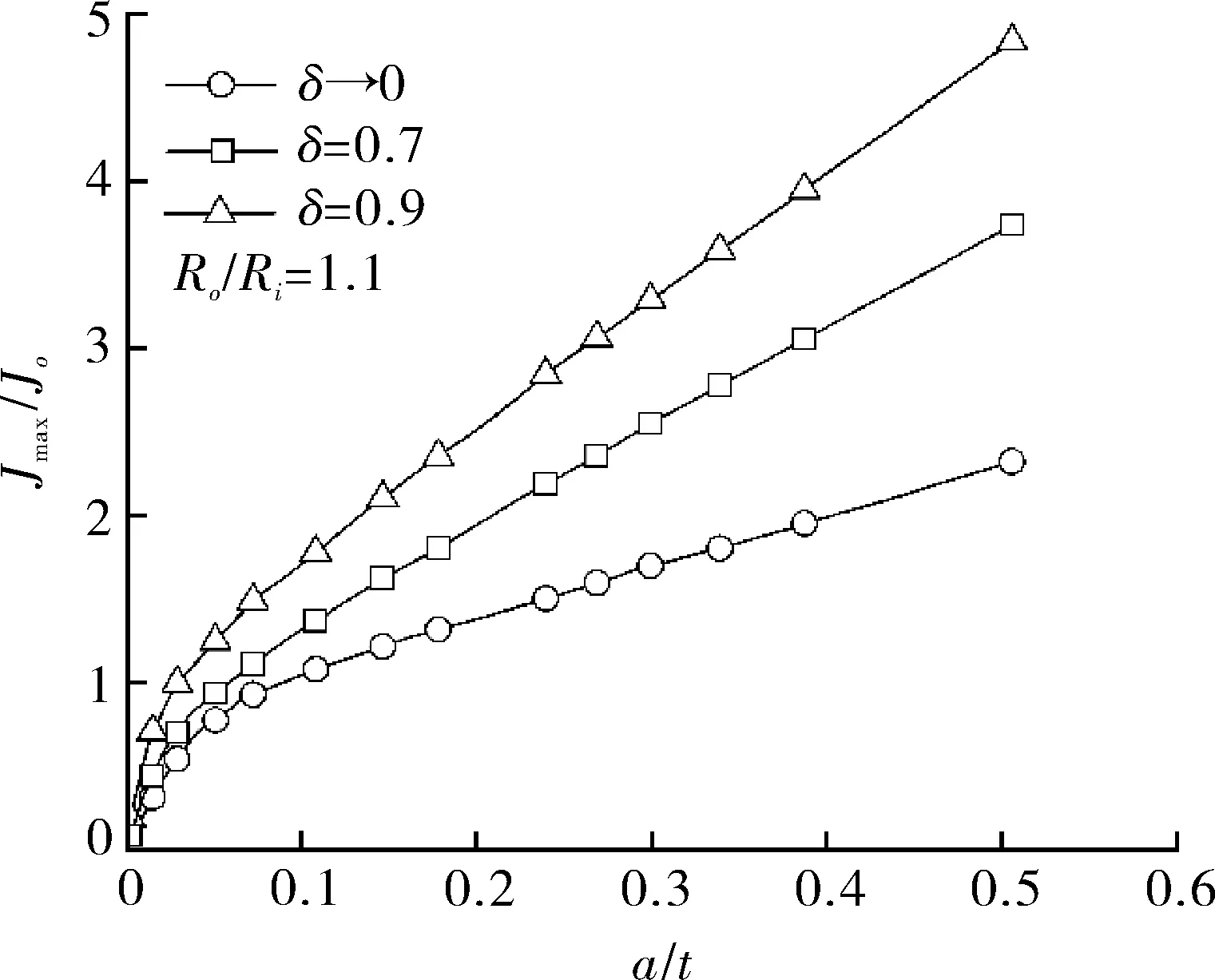
图17 椭圆度a/c=1.0下不同裂纹密率δ对Jmax/Jo变化影响Fig.17 Effect of crack density δ on Jmax/Jo for crack a/c=1.0
相对深度分别为a/t=0.3和0.6,对于椭圆度a/c=1.5裂纹,最大JI/Jo总是位于裂纹尖端ψ=0°附近,如图18所示。对比图18(a)和(b)可以看出,对于相对较浅裂纹a/t=0.3,最大JI/Jo附近的集中分布现象更为显著,如图18(a)所示。实际上,最大JI/Jo一致出现在裂纹尖端ψ=0°附近,并朝着尖端略微减小,如图18(b)所示。
图18和图16相比,a/c=1.5对应的沿裂纹前缘的JI/Jo分布类似于a/c=1.0(圆形裂纹轮廓)的JI/Jo分布。尽管如此,图18揭示了由于较高的裂纹密率δ导致整体上JI/Jo相对较大。此外,随着裂纹密率δ的增加,尖端点附近JI/Jo的下降变得更加显著。比较图18(a)和(b)可以看出,随着裂纹深度a/t的增加,JI/Jo的值虽然变大,但是JI/Jo峰值变得更加平坦。由图18可以看出,无量纲J积分的数据离散度随椭圆表面裂纹深度a/t的增加而增大,此外,还发现JI/Jo数据离散度随裂纹密率δ的增加而增大。J积分的数据离散主要是因为RPV壁厚上的温度分布不均匀,加上沿壁厚方向一次应力、二次应力和峰值应力的共同作用。
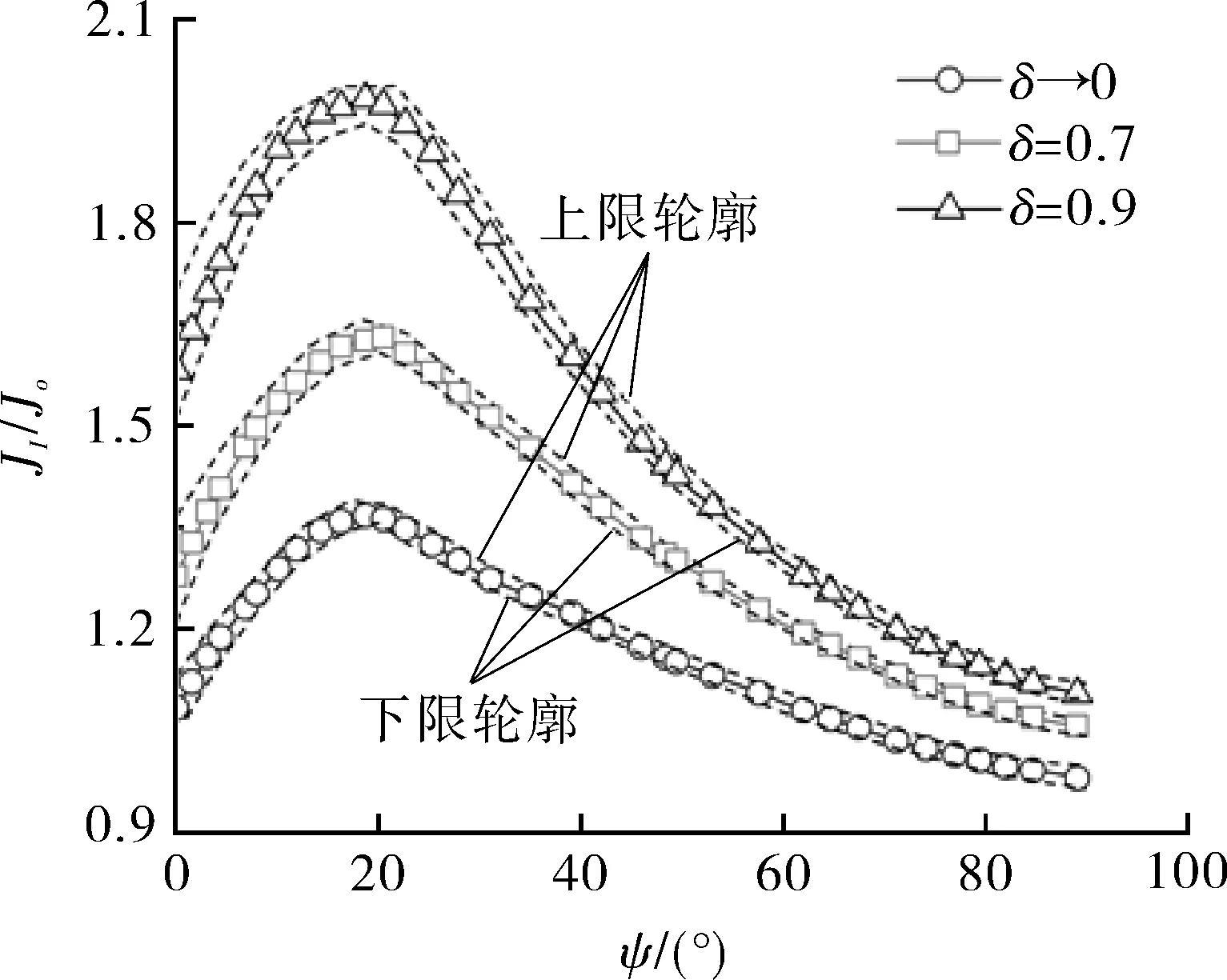
(a)a/t=0.3
椭圆度a/c=1.5下不同裂纹密率δ对Jmax/Jo随a/t变化的影响如图19所示,可以看出,裂纹密率δ对Jmax/Jo-a/t的关系有较大的影响。总体上看,Jmax/Jo-a/t关系曲线还是呈现分段线性和单调增加的特征,另外,随着裂纹密率δ的增加,Jmax/Jo表现为先缓慢增加(0<δ<0.7)、后快速增加(0.7<δ<0.9)。与图15,17不同的是,δ=0.7和δ=0.9对应Jmax/Jo-a/t曲线之间的差值更小,即a/c=1.5椭圆度裂纹的Jmax/Jo绝对值相对a/c=0.3,1.0椭圆度裂纹的Jmax/Jo较小,意味着a/c=1.5椭圆度裂纹对裂纹密率δ的敏感性较低,同样载荷条件下裂纹更不容易扩展。综合来看,同样的裂纹深度a/t下,a/c=1.5椭圆度裂纹在不同的裂纹密率δ下Jmax/Jo的分散性最小,即小于a/c=0.3,1.0椭圆度裂纹Jmax/Jo的分散性。
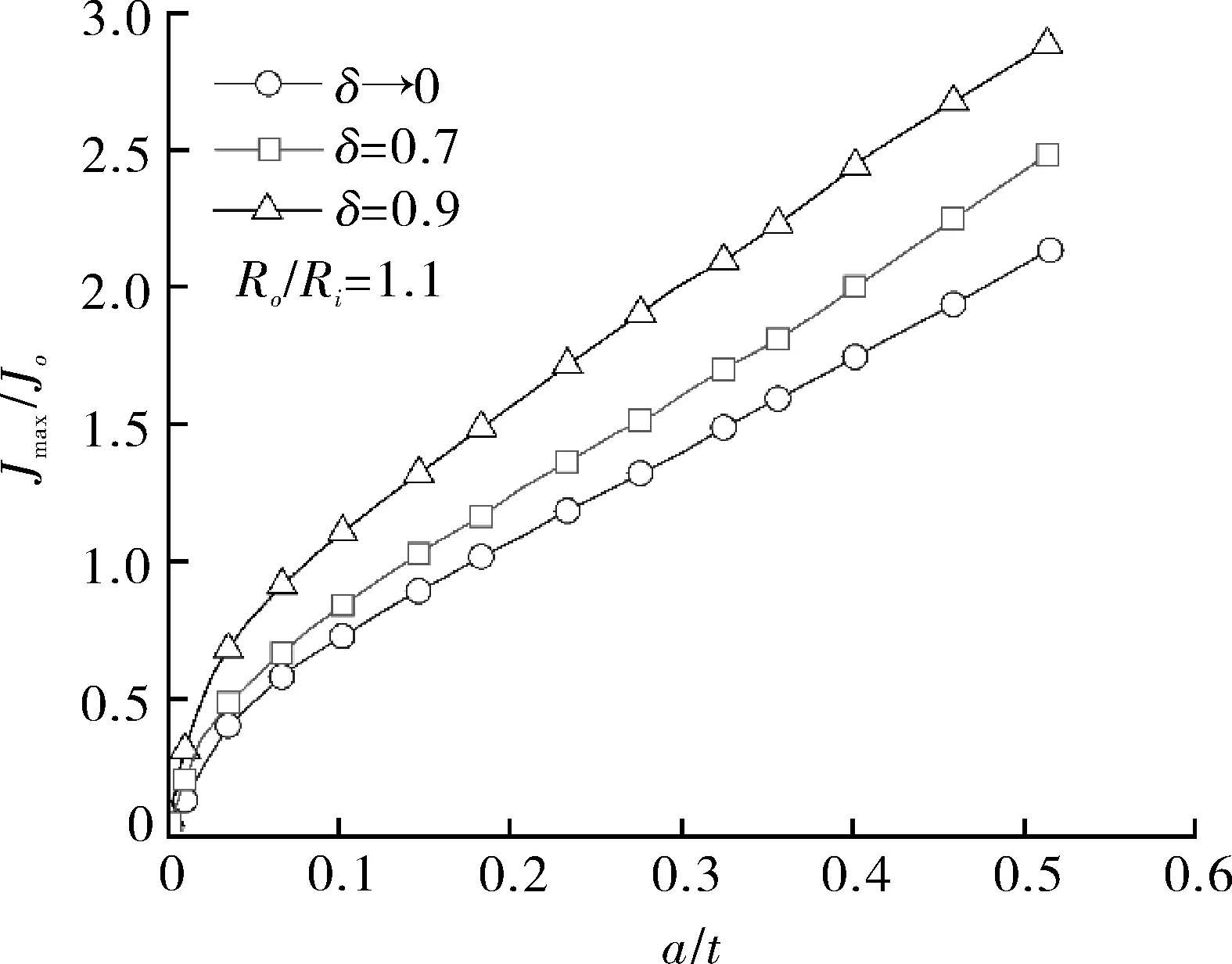
图19 椭圆度a/c=1.5下不同裂纹密率δ对Jmax/Jo随a/t变化的影响Fig.19 Effect of crack density δ on Jmax/Jo with changing of a/t crack a/c=1.5
3 结论
(1)利用热-机耦合下断裂力学方法,研究了堆芯熔毁事故下反应堆压力容器(RPV)下封头的断裂行为。计算了含半椭圆形裂纹的3D裂纹的J积分,考虑了裂纹椭圆度分别为a/c=0.3,1.0,1.5情况。结果显示,对于不同的半椭圆形裂纹,裂纹前缘的J积分分布显著不同,尤其是a/c=0.3的裂纹,其J积分分布与其他两种相反。对于a/c=0.3的半椭圆形裂纹,随着裂纹深度的增加,J积分分布会发生本质性的变化。对于较浅裂纹(a/t=0.3),J积分最大值出现在最大裂纹深度处,而对于较深裂纹(a/t=0.6),J积分最大值出现在ψ=0°的裂纹尖端附近。
(2)裂纹密率δ和裂纹椭圆度a/c是影响RPV压力边界完整性的两个重要因素。随着δ的减小,J积分峰值明显减弱。RPV周围材料对裂纹的稳定作用更为显著。一般,δ=0的J积分约为δ=0.9的J积分的2~3倍。
(3)如果不考虑RPV壁厚上的高温度梯度,势必会错误估算J积分分布和峰值大小,可能会较大地高估和低估J积分值,说明在严重事故条件下对RPV进行断裂力学评价时,热-机边界条件精度对RPV安全设计的重要性。

