基于Fluent的火炮减后坐喷管数值计算与分析

薛 滨，何 永，胡元涛

(南京理工大学机械学院， 南京 210094)

1 引言

在现代战争中，功率增大、机动性提高是传统火炮的发展趋势。体积小、质量轻、射程远、功率大、打击类型多是无人战车发展的重要方向。然而，随着装备火炮的威力增加，对应的火炮后坐力也在逐步增大，因此解决火炮的威力与后坐力的矛盾是十分关键的。

宋杰等对软后坐技术的大口径枪械进行研究，软后坐技术大幅降低了火炮的后坐力，但带来了武器质量增加，首发预压困难的问题。Kathe博士于2000年提出膨胀波火炮的概念，在某一时刻打开火炮喷尾可产生极大的后坐力，但严重影响了火炮的射速。

基于实现火炮减后坐与射速威力的匹配问题，结合对防护工程抗侵彻与毁伤实验，确定炮口初速不得低于860 m/s。本文利用计算流体力学耦合内弹道进行了计算，以某小口径高射速火炮为研究对象，采用了喷管减后坐模型，对喷管的位置进行了合理的选择，实现了弹丸的合理降速和减后坐效率的提高，为未来该小口径火炮与无人作战平台的耦合与装配提供了坚实的理论基础。

2 物理模型

考虑到设计时的身管的硬度与工艺性，模型在距离膛底0.372 9 m处钻了直径与深度均为8 mm的小孔，采用45°转角的导气管转角，并连接向后的喷管，当弹丸底部通过导气孔时打开喷口，此时膛内的火药燃气通过导气孔引向喷管内传递质量和能量，产生反后坐力。该装置的优势在于喷管相对于枪管无运动，枪管受力状态好，工艺性好，能量利用率高，工作可靠性高等。

建立喷管减后坐火炮模型如图1所示。

图1 喷管减后坐火炮模型示意图Fig.1 Nozzle minus recoil gun model

弹丸在发射时，火药在药室内定容燃烧，在弹丸到达导气孔之前，火药仅推动弹丸前进，在弹底到达导气孔之后，一部分气体继续推动弹丸向前运动，一部分气体通过导气孔二次膨胀导入直喷管内，最后通过喷口向外喷出，产生反后坐动量。

3 数学方程

对于气体流动的数值计算，火炮膛内的火药气体参数可由内弹道方程获得。但计算流体力学可以建立火药气体流动的二维和三维模型，利用Fluent软件通过UDF编程耦合一维内弹道模型可对导气孔处三维，喷管内二维流场进行分析。

3.1 变质量内弹道方程

根据膛内火药气体流动特性，建立符合此模型的内弹道方程：

(1)

式中:为火药燃去百分数;为火药已燃相对厚度;为压力全冲量;为内弹道时期膛内平均压力;为燃速指数;为次要功计算系数;为弹丸质量;为弹丸速度;为身管线膛内截面积;为弹丸在线膛内的行程;为导气装置导气孔到膛底的距离;为火药力;为装药量;为绝热系数;为药室容积缩径长;Δ为装填密度;为火药密度;为火药气体余容;′为考虑了火药气体流出膛内的火药燃去百分数修正值;′为药室自由容积的缩径长。未列出的相关内弹道参数可通过参考文献[11]确定。

3.2 导气孔流量和膛内气流参数的确定

在涉及导气装置气流的计算时，需要确定导气孔处膛内气流参数和导气孔最小截面处的流量。

321 膛内气流参数的确定

根据内弹道方程编写内弹道方程组，得到膛内气体的平均压力、温度、密度随时间变化的规律，根据膛内压力的抛物线分布规律，可换算出导气孔处膛内压力、密度和温度随时间的变化规律。

设=0时弹丸到达导气孔处，该处的平均膛压为，=时弹丸到达膛口，导气孔处膛内平均压力为，可得到导气孔处压力关于时间的方程:

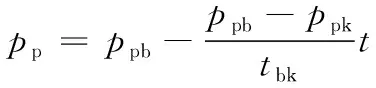
(2)

通过求解内弹道方程组可得=23052×10、=5231×10，=0001 5。因此导气孔处压力时间方程可写为：

=(23052-118 80733×)×1 000 000

(3)

由于火炮在发射过程中某一瞬时温度沿身管的变化量很小，因此在计算中可认为不变，内能可采用平均内能的计算方式：

(4)

式中：、分别为到达导气孔处和弹丸出膛口时的平均内能，由内弹道求解可得=3226 8×10，=2533 8×10。因此的公式可写为：

=(3226 8-462×)×1 000 000

(5)

纵观火药气体从出身管到进入导气孔全过程变化，气流经过导气孔道流动有正流和反流2种状态，并且在正流和反流过程中都可能出现临界流动和亚临界流动的情况，为简化计算，取导气孔气体流动时间为弹丸经过导气孔到达膛口的时间，即0.0015 s，在这个过程中，膛内气体压力恒大于导气管内气体压力，可认为气流均为正向流动。

100 mm坦克炮抽气装置导气孔为35°斜孔，但在实际加工中可知，火炮身管硬度极高，在固定身管打小于45°斜孔时钻头经常会打滑，导致钻头损毁和破裂，因此此次实验所用小口径火炮采用90°垂直孔。在外部添加带有斜角密封式导气装置。经多次实验可勘定90°直孔的流量参数为1.6左右，因此计算取流量参数为1.6。

导气孔处流量、速度、压力、密度与时间的关系如图2所示。

图2 导气孔处参数曲线Fig.2 Parameter diagram at the air guide hole

3.3 控制方程

将模型划分为三维导气管和二维直喷管区域，建立三维非定常N-S微分方程和二维轴对称雷诺平均N-S方程。

笛卡尔坐标系下三维非定常N-S方程的微分形式为：

(6)

式中：为守恒量；、、为对流通量；、、为黏性通量。

=[,,,,]

(7)

(8)

式中：为笛卡尔坐标方向的速度分量；为笛卡尔坐标方向的速度分量；为笛卡尔坐标方向的速度分量为单位气体比内能；为气体密度；，，为热通量分量,为气体压力。

332 二维雷诺方程

喷管内气流具有流动对称性质，建立喷管内对称二维雷诺平均N-S方程：

(9)

式中：为气体密度；为单位气体比内能；、分别为气体轴向和径向速度。

4 计算模型及网格划分

4.1 导气管边界条件及网格划分

为方便计算，将导气管模型进行简化，如图3所示。

图3 导气管模型简化图Fig.3 Simplified diagram of airway model

导气管三维计算模型包含一下3个部分：1/2身管厚度的导气孔，45°的导气喷管，20 mm长的喷管入口。

为精确的监测导气管出口的压力，速度，温度，质量流量等参数，将全局三维模型的网格尺寸设为0.5 mm，采用膨胀型网格对进出口面进行加密。网格划分完成共307 785个单元，71 212个节点。

由于火炮内弹道压力在短时间内有较大的变化、导气管内气流速度较大，因此选择密度求解基，瞬态进行求解。对导气管入口编写UDF程序，共15 000组数据，每个时间步的步长为1e-7，在导气管出口设置监测面，监测静压，动压，温度等参数，共1 500组。

4.2 喷管边界条件及网格划分

建立喷管的轴对称模型如图4所示，边界条件包含喷管入口，喷管出口，中心对称轴，喷管外壁和喷口外壁。

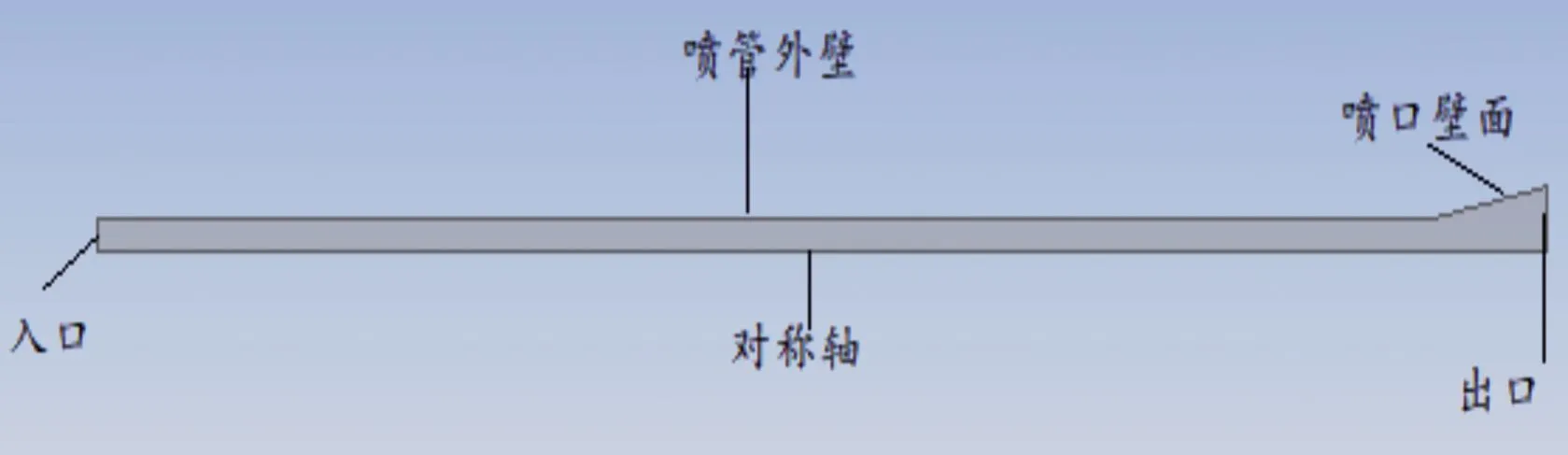
图4 喷管模型示意图Fig.4 Nozzle model diagram

基于喷管的尺寸，将其网格划大小选择为0.5 mm，采用膨胀法对喷管入口，出口进行网格加密，统计划分网格数量可得网格数共23 152个，节点个数共24 113个。采用密度求解基，瞬态进行求解。入口条件由导气孔出口条件计算可得，将导气管出口静压，总压数据编写成UDF，共1 500组数据，单个时间步为1e-6。

5 仿真结果及分析

仿真将导气管与喷管联合起来进行计算，并对仿真结果进行分析，仿真结果展示了导气管的压力速度情况，喷管压力与受力情况，为理论设计计算提供了基础。

5.1 导气管内压力分析

图5展示了不同时刻导气管的压力云图。当弹丸底部经过导气孔时，导气孔打开，火药气体从导气孔内喷出，由于导气管带有斜度的特殊情况，身管直孔喷出的火药气体不断冲刷导气管外壁和喷管外壁。=0.2 ms时刻为火药气体压力流出的最大时刻，此时导气管外壁最大压力为280 MPa，喷管外壁最大压力为180 MPa；此后流出压力不断减小，对导气管和喷管的压力冲刷也在逐渐减小。=0.6 ms时导气管外壁最大压力为190 MPa，喷管外壁最大压力为110 MPa；=1 ms导气管外壁最大压力为130 MPa，喷管外壁最大压力为80 MPa；监测压力是发现0.6 ms时刻出口压力有一定的波动，这是由于导气管的特殊结构使得有一定的压力回流，属于正常现象。

图5 导气管不同时刻压力云图Fig.5 Pressure diagram of the airway at different times

5.2 喷管内压力与喷口处速度分析

本研究中针对9°，10°，11°，12°喷口对喷管进行了受力分析与对比计算，因采用12°为基准，本节压力与速度分析以12度喷口为例。

由图6、图7所示，=0.5 ms时为喷管压力流入初期，喷管内最大静压为26 MPa，喷口处最大速度为1 700 m/s，因导气管结构的影响，静压与实验测得有所波动。=1 ms时为喷管压力注入中期，此时膛内最大压力仍为26 MPa，但在21 MPa左右区域产生了少量的回流，这是由于最大压力流动位置的改变，压力有从高压区流向低压区的趋势，但是会被导气管出口补足的压力抵消。=1.5 ms时为计算结束时期，此时膛内压力仍有20 MPa，出口速度降至1 300 m/s。

图6 喷管不同时刻压力云图Fig.6 Pressure diagram of nozzle at different times

图7 喷管不同时刻速度云图Fig.7 Velocity diagram of nozzle at different times

5.3 多角度喷口受力计算与分析

由于不同角度下喷管的受力情况都不相同，为寻求最优的喷管角度。本节对不同角度下喷口受力进行了设计与计算。结果显示，喷口受力最大值为2 161.78 N，火炮受力最大值为56 000 N，该结果与实验值吻合。

火炮炮膛面积与喉部面积比()，药室进口面积同喷管喉部面积比()，喷管出口面积与喷管喉部面积()，喷管扩张角()4个参数是喷管设计的基础。这些参数的选择是根据喷管设计理论和喷管设计性能分析共同决定的。

考虑到气流在喷管中的膨胀时间与火炮后坐的时间匹配性，取为128，为170，为40，扩张角在9～16°。

扩张角过小时，能量损失增加。扩张角过大时，气流速度受到极大的影响。在实验中发现，喷管角度大于12°时喷管受力没有太大的变化，因此修正喷管扩张角在9°～12°。

喷管扩张长度的计算公式如下：

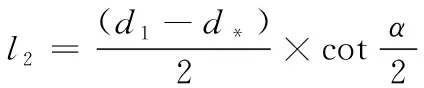
(10)

式中：为喷管出口直径；为喷喉直径。经计算求得4个角度扩张段长度分别为28.22、30.86、34.027、37.88 mm。

在火药燃气后喷的过程中，后喷装置的喷管内壁为主要受力部分，受力大小如图8所示。9°～12°喷口受力大小如图9所示。

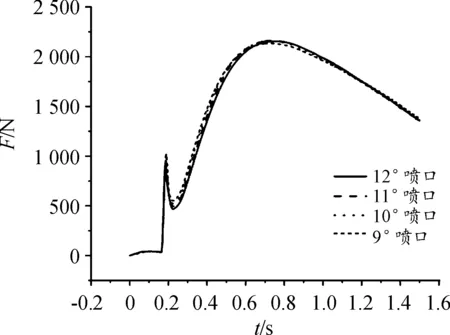
图8 喷管受力曲线Fig.8 Nozzle load diagram

图9 不同角度喷管受力曲线Fig.9 Pressure diagram of nozzle at different angles

由图9可知，9°喷管受力最大值为2 132.88 N，所受冲量为2.25 N·S。10°喷管受力最大值为2 154.29 N，所受冲量为2.24 N·S。11°喷管受力最大值为2 161.78 N，所受冲量为2.16 N·S。12°喷管受力最大值为2 154.61 N，所受冲量为2.15 N·S。

求解减后坐效率可以通过求得火炮的炮膛合力和冲量，并与同等条件下闭膛火炮炮膛合力冲量进行比较。

该火炮发射的是杀爆弹，弹丸质量为0.391 kg，泄压前后速度变化如图10所示。由图10可以看出，泄压前弹丸出膛口时最大速度为933 m/s，泄压后弹丸出膛口速度为857.8 m/s。弹丸初速降低8%。

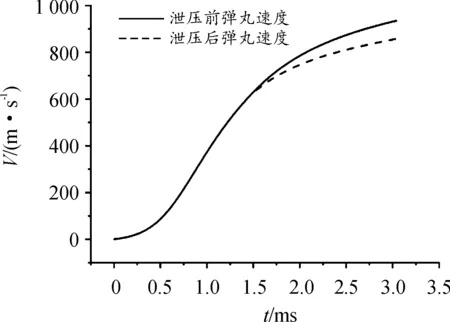
图10 泄压前后速度曲线Fig.10 Velocity variation before and after pressure relief

将弹丸速度带来的冲量减和喷管带来的冲量减相加，与弹丸未降速时的冲量对比。为开孔泄压时，火炮所受最大冲量为365.41 N·S，开孔泄压后，火炮所受冲量为332.34 N·S。如图11所示。

图11 冲量曲线Fig.11 Impulse contrast diagram

将弹丸速度带来的冲量减和喷管带来的冲量减相加，与弹丸未降速时的冲量对比。为开孔泄压时，火炮所受最大冲量为364.80 N·S，开孔泄压后，火炮所受冲量为332.34 N·S。对比结果如图11所示。

由自由后坐动能计算方法可得减后坐动能公式为：

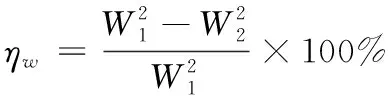
(11)

式中：为未泄压前身管所受冲量；为泄压后身管所受冲量。将上述数据代入可得，该喷管减后坐效率的值为173，该结果与实验结果相吻合。

6 结论

利用Fluent软件对火炮减后坐喷管装置内火药气体流动进行仿真计算，并对计算结果进行分析，可以得出以下几点结论：

1) 将整根火炮减后坐喷管装置拆解为导气管与直喷管并将其放入Fluent中对其进行三维模型与二维模型的计算不仅能准确的获得仿真结果，还能有效地提高工作效率。

2) 带有减后坐喷管装置的火炮损失较小的弹丸初速即可获得相对较大的制退效率，将其与膛口减后坐装置结合并进行下一步研究有着重要的意义。

3) 导气管采用45°斜角以获得高效的导气效率，但由仿真结果可知，导气管入口外壁与直喷管入口外壁会受到较大的压力冲击，在设计时应对这2个部位的材料加厚，保证导气装置的耐用性。