基于灰色关联和比例风险模型的装备环境影响因素分析

李逸源,杨江平，谢雨希，胡 欣

(1.空军预警学院，武汉 430014； 2.中国人民解放军93498部队， 石家庄 050000)

1 引言

环境是雷达装备在实际使用过程中无法回避、时刻受其影响的重要因素.装备性能指标和作战效能均与环境因素有着密切的关系，装备保障数据既包含装备历史故障信息，也包含工作环境信息。充分挖掘装备保障数据，研究复杂环境因素对装备故障的影响，对于实现智能化装备保障有着重要意义。目前，关于环境因素对装备故障影响的研究大致分为以下2类。

一类是定性分析装备在使用过程中面临的环境以及这些环境对装备造成的影响。文献[1]通过总结高原地区的气候特点，分析了高原气候因素对防空武器装备各分系统的影响,并提出了相应的改进措施。文献[2]选取高温、高湿、高盐3种典型的复杂环境因素，研究其对雷达装备的腐蚀机理。这类方法多为理论分析和定性论述，其研究数据也大多基于研制阶段的试验数据，没有充分结合装备实际故障数据。

另一类是基于环境因子定量表征不同环境对装备可靠性的影响程度。文献[3]基于寿命数据提出环境因子模型，分析多种环境因素对装备可靠性的影响。文献[4]利用装备研制阶段的试验数据，引入环境折合系数对不同试验条件下的装备可靠性进行综合评估。这类方法通常假设不同环境条件下装备的失效机理一致且服从同一形式的寿命分布，该假设在实际工作环境下难以验证，限制了方法的适用性。

针对装备保障数据利用率不足和装备在不同工作环境下寿命分布难以确定的实际问题，本文引入灰色关联分析法和比例风险模型，分别从定性和定量2个角度，研究了实际工作环境下复杂环境因素对装备故障概率的影响。通过Cox比例风险模型，构建装备在实际工作环境下的可靠度函数，将环境变量参数代入进行寿命预测。将故障记录中的故障间隔时间与装备寿命预估值进行对比，验证了分析结果的准确性。

2 基于灰色关联分析的定性分析法

灰色关联分析是按发展趋势作分析，既不需要很大的样本量，也不需要典型的分布规律，因此本文引入灰色关联分析法，探究不同工作环境对装备分系统故障的影响。其实质是将不同环境下各分系统故障次数的最大值与各分系统的故障次数进行量化比较。根据彼此差异值，分析不同工作环境与分系统故障频率之间的关联程度。灰色关联分析的步骤如下。

1构建决策矩阵。

(1)

式(1)中：)×表示在个不同的工作环境下，个分系统所对应的故障次数。

2归一化处理。在决策矩阵中不同指标的数在大小上相差较大，因此采用均值化法进行归一化处理，使得同一指标下的数量级相同。均值化变换公式为：

(2)

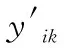
3确定参考数据序列与比较数据序列。对各个因素进行关联分析前，首先要确定参考数据序列。设经过归一化处理后的决策矩阵为′，求得′中每一行的最大值，即为各分系统在不同工作环境下的故障次数最大值，即：

(3)

设定参考数据序列()为：

(4)

设定比较数据序列()为：

()=(=1,2,…,)

(5)

4计算关联系数。

(6)

式(6)中，为分辨系数，∈(0,1]，越小，关联系数的分辨力越高，一般取=05。

5计算加权灰色关联度。假定各工作环境的重要度相同，因此令权系数=1，则各分系统与工作环境之间的灰色关联度为：

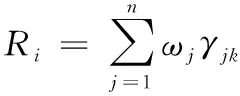
(7)

6关联度排序及关联规则提取。将各个故障分系统与工作环境之间的加权灰色关联度进行大小排序。关联度数值越大，表明该分系统受环境因素的影响越大，从而提取出相应的关联规则，定性分析不同工作环境对装备分系统故障的影响。

3 基于比例风险模型的定量分析法

3.1 Cox比例风险模型

比例风险模型由英国统计学家Cox于1972年首次提出，其风险函数表达式为：

(8)

式(8)中，为第个可能与装备故障相关的协变量，也称为故障影响因素；为协变量所对应的回归系数，为正，表示协变量与装备故障风险正相关，为负，表示协变量与装备故障风险负相关；为协变量的个数；()为基准风险函数，它是指所有风险因素为0时的基础风险率，与协变量无关，在实际应用中可以不用考虑它的分布形式，因此比例风险模型又称为半参数模型。风险函数可以转化为累计生存函数(),表征装备在时间内正常运行的概率，其表达式为：

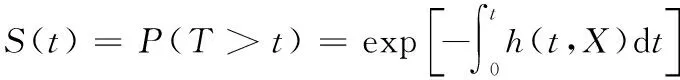
(9)

3.2 PH假定检验

Cox比例风险模型在实际应用时需满足PH假定，即模型中协变量对生存率的影响不随时间而改变。PH假定的判断方法有图示法和交互作用判断法等2类。图示法通过比较生存曲线间是否大致平行来判断PH假定的成立，操作简单但存在一定的误差。因此，本文选用后者判别PH假定检验，此时模型的表达式(,)为：

(,)=()exp(+lg())

(10)

式(10)中：lg()为协变量与时间的交互作用项；为协变量系数。对引入交互作用项的模型(,)进行假设检验，原假设H:模型参数为0。根据显著性检验方法得到原假设的值，通过检验值进行判断。若>005，原假设成立，表明协变量与时间的交互作用不明显，满足等比例风险假设。反之，若<005则拒绝原假设，协变量不满足PH假定检验。

3.3 模型构建方法

假设某型装备在不同工作环境下一共收集到n条故障数据，构建比例风险模型需要的数据形式可用一个三元组来表示，记为(X，T，δ)(i=1,…,n)。其中，协变量X为对装备故障造成影响的环境因素。雷达装备工作环境中存在高山、沿海、戈壁这类复杂恶劣的地理与气候环境，其中高山环境气候特点为低温、低压，对电子元件散热与放电均会产生影响；沿海环境气候特点为高温、高湿，并且沿海盐雾大气会对雷达装备的结构部件和电子设备造成腐蚀；戈壁环境气候特点为干燥，风沙大，易造成雷达装备机械器件磨损，并且风力过大时严重影响伺服控制性能。考虑到雷达装备工作环境的实际特点，为进一步量化环境因素的影响程度，因此，本文重点选取现场温度、现场湿度、海拔高度、风力等级、大气压力这5类环境因素作为协变量。T为寿命数据，由于雷达装备是可修复系统，因此T可视作装备故障间隔时间。δ为示性变量，表示数据的删失状态。在比例风险模型中，根据删失状态可将寿命数据T分为2种类型：一种是在观测期内已经发生下一次故障的寿命数据，删失状态δ=0，T即为2次故障之间的时间长度；另一种是在观测期内未发生下一次故障的寿命数据，删失状态δ=1，T即为本次故障到观测终点之间的时间长度。

4 实例分析

4.1 数据集

本文以某型雷达装备作为研究对象，收集整理了其在高山、沿海、平原、戈壁等4种典型工作环境下共计1 345条装备保障数据作为原始数据，其中包含3个部分信息：其一是装备的基本信息，包括所在单位、装备型号、出厂编号、技术等级、工作环境等；其二是装备的故障数据信息，包括故障时机、故障现象、故障部位与原因、维修情况等；其三是装备的环境影响因素，包括现场温度、现场湿度、海拔高度、风力等级、大气压力等。

通过对这些数据进行初步统计分析，提取出不同环境下各个分系统的故障频率，得到故障分系统占比直方图，如图1所示。由图1可知，接收分系统、发射分系统、监控分系统是影响雷达装备正常运行的主要分系统，但是不同环境对于分系统故障的影响还需要进一步分析。

图1 故障分系统占比直方图Fig.1 Primary and secondary diagram of fault sub-system

在进行故障影响因素分析之前，需要对原始数据进行预处理，预处理原则如下：

1) 依据GJB899A—2009对故障分类的定义，故障可分为责任故障和非责任故障，只有责任故障才是用于可靠性验证试验统计故障。本文研究环境因素对装备可靠性的影响，需要将原始数据中属于非责任故障的故障记录剔除，如误操作引起的故障、因测试仪表故障而引起的故障、修复过程中引入的故障等。

2) 本文研究的环境影响因素均为连续变量，在故障记录中存在少数异常值。这类异常值可能为极端天气情况或人为记录出错导致，对分析结果的准确性存在较大影响，因此依据拉依达准则，对数据异常值进行剔除。

以现场温度数据为例，设故障记录中的数据值为,,…,。

算术平均值为：

(11)

绝对误差为：

(12)

根据贝塞尔公式，计算数据的标准误差为：

(13)

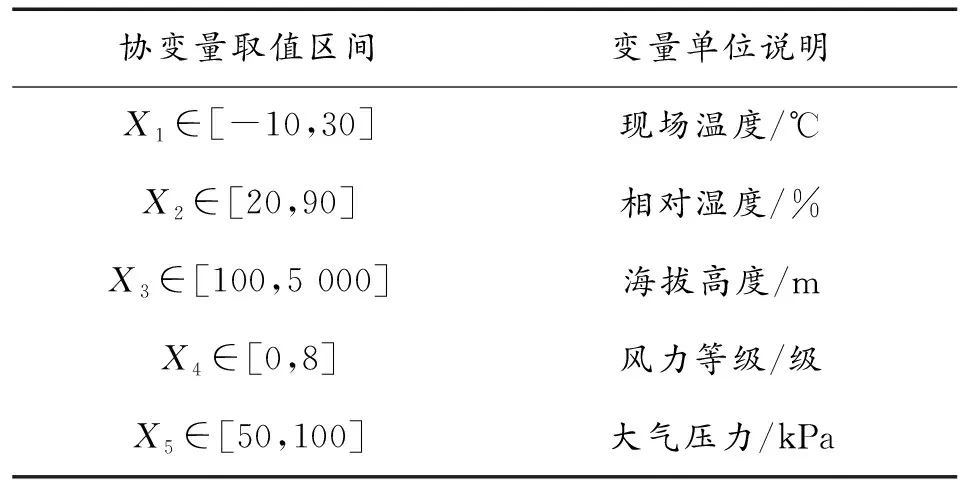
表1 各协变量取值区间Table 1 Description of each covariate

3) 本文假设装备寿命分为2类：一类是完整的寿命周期，即2次相邻故障时间间隔，由2次相邻的故障记录中累计工作时间相减得到，删失状态记为“0”；另一类是右截尾数据，即在截止观测期内装备正常运行未发生故障，由截尾日期内累计工作时间减去前一次故障累计工作时间得到，删失状态记为“1”。所采用的时间尺度统一为小时(h)。

按照上述预处理原则，整理出完整样本876条，右截尾样本249条。表2为数据集样例。

表2 数据集样例Table 2 Sample data set

4.2 灰关联分析

将数据集中的工作环境作为关联对象，以各分系统的故障次数作为关联指标。通过式(2)将各分系统的故障次数进行归一化处理。通过式(3)～(5)选定参考数据序列和比较数据序列，得到灰色关联分析数据，如表3所示。将上述数据代入式(6)和式(7)，得到各个分系统与工作环境之间的灰色关联度，结果如表4所示。

表3 故障分系统灰色关联分析数据Table 3 Grey relational analysis data of fault sub-system

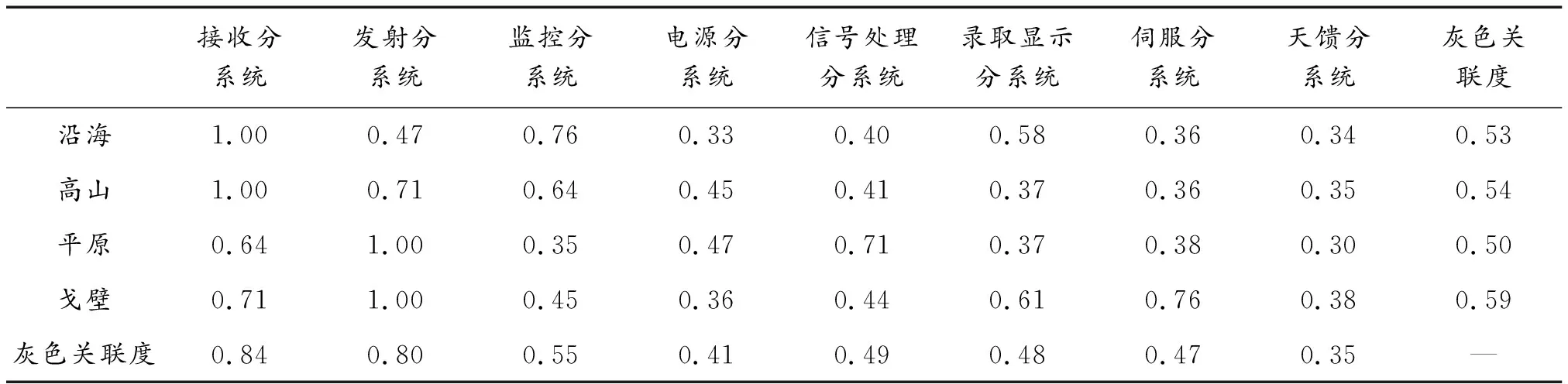
表4 故障分系统灰色关联分析结果Table 4 Grey relational analysis result of fault sub-system

依据灰色关联分析结果，提取到的关联规则如下：

1) 可靠性受工作环境影响最大的分系统分别为接收分系统(0.84)、发射分系统(0.80)、监控分系统(0.55)；

2) 沿海和高山环境下，接收分系统可靠性受环境因素影响最大；

3) 平原和戈壁环境下，发射分系统可靠性受环境因素影响最大；

4) 不同工作环境下对装备分系统的故障影响排序为：戈壁>高山>沿海>平原。

4.3 PH假定检验

本文使用SPSS25软件对雷达装备保障数据进行Cox回归分析。将待检验变量转化为时依协变量*In(),即在模型中引入一个含时间与变量的交互作用项。然后，检测该项的显著性，分析结果如表5所示。

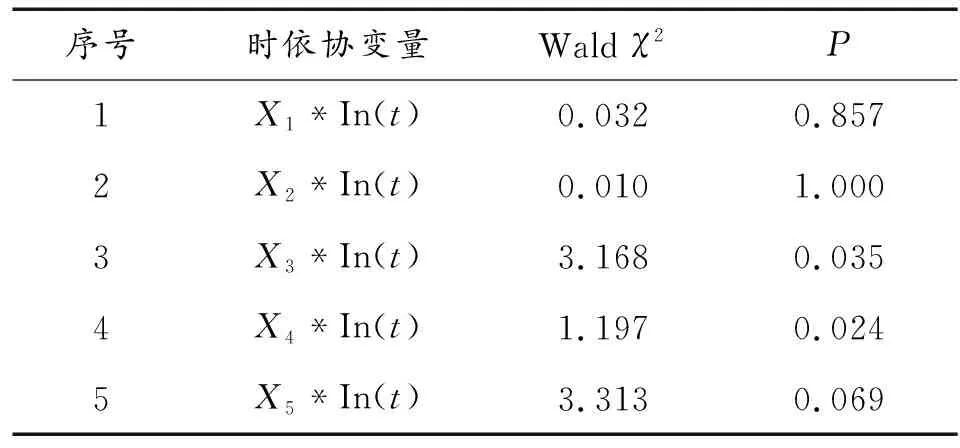
表5 PH假定检验分析结果Table 5 PH hypothesis test

由表5可知，时依协变量1、2、5的值均大于0.05，满足PH假定，即可应用Cox比例风险模型。

4.4 生存分析

由于雷达装备是由多个分系统组成的复杂电子设备，不同分系统的物理结构和运行机制各不相同，因此其故障规律也会有较大差异，需要对每个分系统作单独分析。通过灰关联分析得到接收分系统可靠性受工作环境的影响最大，因此本文优先选择以接收分系统作为研究对象，进行生存分析。

使用SPSS 25软件，以现场温度、现场湿度、大气压力等3个协变量构建Cox比例风险模型。设置原假设：=0时，协变量与雷达装备故障无关。通过wald检验，检验原假设。当值大于005时接受原假设，认为协变量与雷达装备无关；当值小于0.05时拒绝原假设，协变量与雷达装备故障相关，结果如表6所示。

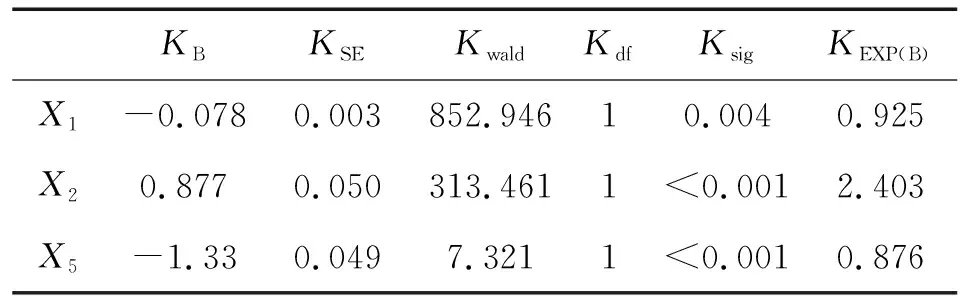
表6 方程中的变量Table 6 Variables in the equation

表6中，对应于模型中的估计值、表示估计值的标准差、表示估计值的Wald统计量、表示自由度、表示Wald检验的值、表示相对危险比。

由表6可得，协变量、、的值均小于005，通过显著性检验，对装备故障风险存在统计学意义。其中，现场温度的系数为-0078，表明当环境温度处于-10 ℃～30 ℃时，装备的故障风险与环境温度呈负相关。对于电子设备，低温通常有利于散热，分析结果看似与这一常识相悖。然而，由于部分样本来自于高原低温环境，气温过低会造成雷达装备无法开机、功率下降、探测距离衰减并且严重影响电源性能，从而大幅度降低装备可靠性。因此，综合分析，低温环境对于装备可靠性的影响更大。现场湿度的系数为0877，表明当相对湿度在20～90时，装备的故障风险与环境温度呈正相关。这是因为潮湿环境下，对雷达装备整体的电气性能和机械性能都有着明显的影响。潮湿环境极易造成金属氧化或者电化学腐蚀，从而降低机械性能，此外元器件、印制板、连接件等电子设备的介电强度和绝缘性能也会下降，导致短路或断路。大气压力的系数为-1.33，表明装备的故障风险与大气压力呈负相关。这是因为气压过低时，空气密度下降，导致电子产品空气绝缘耐压降低，对电子设备的性能影响很大。特别是对于雷达这类复杂电子设备，气压的下降还可能会导致高压部件绝缘下降，出现打火、放电等现象。

4.5 模型预测

通过求解各协变量的相关系数，代入式(8)和式(9)，即可得到装备的风险函数和累计生存函数，将特定的协变量参数代入生存函数中，即可估计相应工作环境下装备在一定工作时长内的可靠度。以数据集中某一样本为例，现场温度 9 ℃，相对湿度22%,大气压力89.9 kPa，故障间隔时间为 275 h，将协变量参数代入模型，得到装备在一定工作时长内的生存概率,如图2所示。

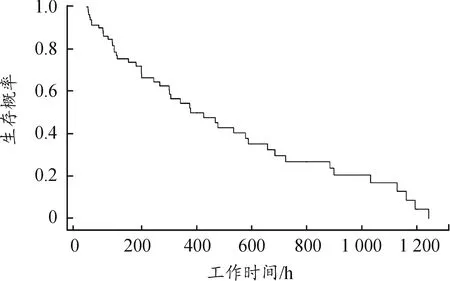
图2 生存分析函数曲线Fig.2 Survival analysis function graph

通过Cox比例风险模型的构建，计算出装备在指定协变量参数下的生存概率。为检验预测结果的合理性，需要一个合理的判断标准。定义装备故障间隔时间为的判断阈值为：

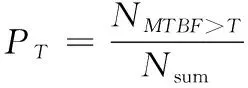
(14)

式(14)中：分子为故障间隔时间大于的样本数；分母为建模所用总样本数。如果计算样本在时刻的生存概率小于该时刻的阈值，则判断该样本在时刻会发生故障。通过样本计算得到各个时刻的阈值如表7所示。

表7 预测结果的判断阈值Table 7 Judgment threshold of prediction result

从图2可知，装备在运行300 h后，其生存概率低于0.6，小于=300 h时的阈值，因此可以判断装备在=300 h内已经发生故障。由该样本实际数据可知，其故障间隔时间为275 h<300 h，因此模型预测结果具备一定的合理性。

4.6 预测结果的可信性与鲁棒性分析

为检验预测结果的可信性，按照8∶2的比例将数据集划分为训练集和测试集。首先使用训练集中的样本构建比例风险模型，进行生存分析。然后将测试集中的样本协变量参数分别代入模型得到生存概率并与阈值比较，计算出模型预测的准确率，结果如表8所示。

表8 模型预测的准确率分析Table 8 Model accuracy analysis

由表8可知，模型判断装备发生故障的准确率为89.62%，判断装备正常运行的准确率为82.81%，综合预测准确率达到87.43%，在实际运用中具备一定的可信性。

为检验预测结果的鲁棒性，排除模型可能受到不同样本的影响。按照相同比例对原始数据随机抽取3次，组成新的数据集分别建立模型，并计算模型预测的准确率。选取预测时间为100 h、200 h、300 h，计算结果如表9所示。

表9 模型鲁棒性分析计算结果Table 9 Model robustness analysis

由表9可知，基于这3组数据建模，预测准确率与前文结果比较接近，并且模型的预测结果都较为精确。因此，模型的分析结果具备一定的鲁棒性，受样本的影响较小。

5 结论

采用灰色关联法和Cox比例风险模型，从定性和定量2个层面分析了环境因素对雷达装备的故障影响，并通过实际数据验证了分析结果的准确性。本文提出的方法能够充分挖掘雷达装备保障数据，提高数据利用率，对于装备可靠性数据分析与环境适应性研究均有参考价值。