基于WRF模式的初始场误差分析方法

刘公铄，杜英森，李 岩，冀宵玉，孙 琦

(1.南京理工大学 能源与动力工程学院，南京 210094；2.西安机电信息技术研究所， 西安 710065)

1 引言

在现代战争中，随着战场节奏加快，对于火炮武器的射击有着“首发命中”、“首群覆盖”等打击要求。如何使弹丸在保证射程的条件下，提高火炮武器的打击精度，是国内外火炮武器的重点研究方向之一。而随着目前火炮武器射程的提高，气象条件对弹道的影响会随着弹丸出膛后射程的增加而增加，成为了影响火炮武器打击精准程度的重要因素。

目前世界各国主流的火炮气象保障中，无论是通过探空气球、探空雷达、无线经纬仪GPS等设备进行气象数据测量，都难以反映整个弹箭外弹道区域气象条件的变化。数值气象预报由于能够通过数值计算，可以快速实时地向火炮外弹道区域提供气象保障，且具有高精度网格化气象数据，充分弥补了目前火炮气象保障的不足。

对于数值气象预报存在的误差，主要原因是由初始场误差，模型误差和计算误差造成的，初始场误差即模式初始场不确定性，也就是模式初始场和实际大气之间的偏差。而数值气象预报的初始场误差是从数据源头上影响数值气象预报误差的因素，初始场能否反映真实的大气运动，直接从数据源层面影响模式的预报结果。

影响数值气象预报初始场误差的因素主要有气象观测误差和网格设置所造成的边界误差。气象观测误差是气象站观测中的观测误差，又由于气象站位置并非实际的炮射坐标位置，因此需要利用数值模式对初始场进行空间网格划分，在网格划分的过程中会由于插值算法以及边界条件设置造成初始边界误差。

在目前气象观测设备精度日益完善的条件下，影响数值气象预报初始场误差的主要因素就是初始边界误差。针对WRF(weather research and forecasting,WRF)这种中尺度数值天气预报模式，马晨晨等采用次网格参数化方案，使模拟初始场条件更贴合实际气象条件，准确率、相关性都有明显提高，模拟误差明显降低。于佳兴、曹树新等设计了一种较为准确和快捷的网格划分方法，运用到WRF模式的前处理过程中，提高了数值天气预报初始场的准确度。在目前的研究当中虽然提高了数值天气预报初始场的精准度，但优化后的初始场条件多用于大气科学研究，不适合于弹箭外弹道计算用。本文在数值气象预报误差研究基础上，基于WRF模式对我国东北地区进行初始边界设置，针对模式输出的初始参量采用大气热力学公式换算成外弹道气象诸元，选用了平均误差、平均绝对误差、均方根误差和相关系数4种气象学指标评估初始场误差,并结合弹箭六自由度方程组，以仿真弹道的最终落点评估初始场误差的影响。为之后数值气象预报初始场误差的修正、提高数值天气预报的预报精度奠定基础。

2 系统模型

2.1 WRF模式前处理过程

WRF模式是由包括美国国家大气研究中心(national center for atmospheric research,NCAR)等多个部门联合研究发展的新一代中尺度数值模式，是目前世界上进行数值气象预报研究的主要模式之一，因此本文选择用WRF模式进行研究。WRF模式系统主要由前处理、WRF基础软件框架和后处理三大部分，而在数值天气预报的初始场误差研究当中，主要研究的是WRF模式的前处理过程，WRF模式的前处理系统(WRF preprocessing system,WPS)主要是为模式做前期的数据准备，其具体过程主要包括：定义模拟区域和嵌套区域、计算格点经纬度，地图投影放大系数和科氏系数、将陆面数据插值到模拟区域、将随时间变化的气象数据插值到模拟区域。

2.2 WRF模式参数设置

本研究当中设置的区域位于我国东北地区，并对WRF的前处理阶段进行参数设置，散发结构采用的是单重网格结构，格点数设置为121×121，格点间水平间距设置为4 000 m,格点的垂直层数设置为81层，模式的顶层气压为1 000 Pa。另外，WRF模式的初始场资料采用的是NCEP于当日0时(世界时)发布的0.25°×0.25°再分析资料，并采用空间插值法得到该气象点垂直方向上的数值气象数据，其中空间插值法选用普通克里金(ordinary kriging,OK)插值方法，WRF的数值模型见参考文献[3]。

2.3 弹道模型

本文通过将弹道数据与气象数据相联系构建弹丸运动模型，将气压、虚温、风速和风向的初始场误差值代入到弹道模型当中，可以更直观地看出数值天气预报的初始场误差对火炮打击精准度的影响。

在有风条件下，通常将风速和风向分解为纵风和横风：

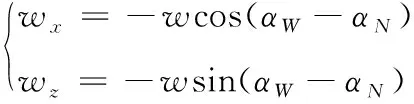
(1)

其中:纵风主要影响弹道的射程；横风主要影响弹道的侧偏；为风速；为风向；为射向。

在有风条件下弹丸的相对速度为：

=-

(2)

其中：为相对速度矢量；为相对风速矢量此时产生的空气动力和气动力矩为：

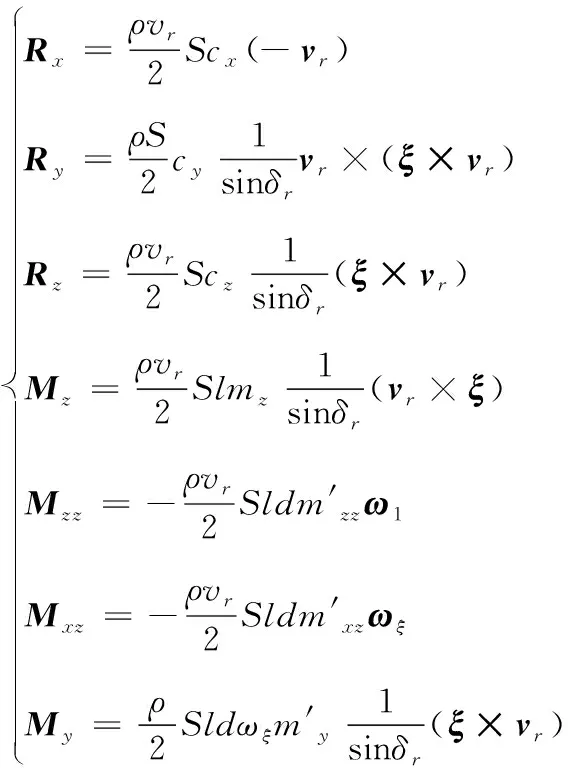
(3)

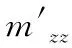
3 外弹道气象诸元误差获取方法

3.1 外弹道气象诸元的转换方法

在前处理系统计算处理后会输出包括大气要素、陆面要素、土壤要素、海洋要素在内的206个要素变量，而在使用过程中，需要从这些输出变量中选取主要影响外弹道计算的变量。本文中选取主要影响弹丸打击精准度的外弹道气象诸元有风速、风向、虚温和气压。风速和风向可分解为纵风和横风，分别影响弹道的射程和侧偏；虚温和气压通过影响大气密度和马赫数，进而影响弹道解算的精度。由于这4个气象条件不能通过WRF模式直接计算得到，因此需要对WRF模式输出计算得到的数据进行转换，以得到外弹道计算需要的气象计算条件。WRF模式输出的变量中与外弹道气象诸元相关的变量如表1所示。

表1 WRF模式输出的相关变量Table 1 Related variables output in WRF model

1) 风速和风向

结合纬向风速和经向风速并通过矢量合成可得到风速和风向：

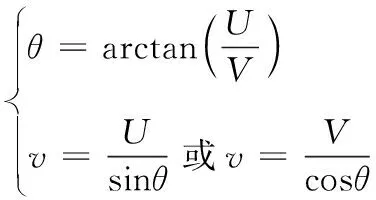
(4)

因WRF输出的每个变量处于空间网格的不同格点，为便于后续计算，需要将非质量点处的变量移动到质量点处，即将与质量点相邻的2个格点、2个格点分别取平均，作为质量点处的纬向和经向风速。

2) 气压

在气象学当中，利用WRF模式输出的扰动气压和基准态气压相叠加可以获得弹道计算用气压条件，公式为：

=+

(5)

其中气压的单位均为帕(Pa)。

3) 虚温

对于弹道计算中虚温的计算公式为：

=(1+0608)

(6)

其中:为气象学中的气温，结合扰动位温、扰动气压和基准态气压可以得到；为比湿，比湿是湿空气中的水汽质量与湿空气的总质量之比，可以通过水汽压得到。这2个条件的计算方法如下：

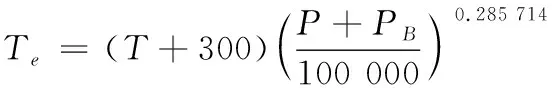
(7)

(8)

其中：气温和虚温的单位为开尔文()；E为水汽压,水汽压是空气中水汽的分压强，目前有多种计算经验公式，本文中选用改进马格纳斯(Magnus)经验公式计算得到：

3.科研创新能力：三级指标主要包括参加科研活动的情况、发表专业学术论文的情况、创新活动参与情况、创新素质。

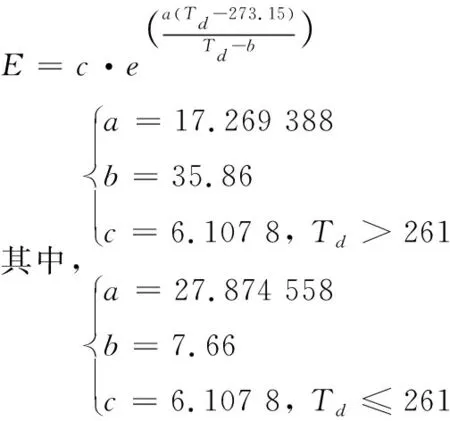
(9)

其中：为露点温度，露点温度是指空气在水汽含量和气压都不改变的条件下，冷却到饱和时的温度，它可以直接通过WRF模式输出。将式(7)～式(9)代入到式(6)当中，可以得到外弹道计算中所需要的虚温条件。

3.2 数值气象预报中的误差获取方法

对于连续变量数值气象预报的误差，主要从平均误差(Mean Error，ME)、平均绝对误差(Mean Absolute Deviation，MAE)、均方根误差(Root Mean Squared Error，RMSE)、倾向相关系数(Correlation Coefficient，R)、距平相关系数(Anomaly Correlation Coefficient，AC)、误差标准差(Standard Deviation of Error，SIDE)6个方面获取。由WRF模式输出的数据为区域模式下数值气象连续变量预报数据，因此采用ME、MAE、RMSE、R四个公式综合对气压、虚温、风速、风向4种外弹道气象条件进行误差评估。

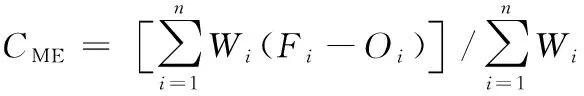
(10)

式中:为平均误差，表示模式的气象预报误差倾向。每层气象数据样本为，第个样本的气象预报值为，第个样本预报对应的实测数据为，为权重系数。

(11)

式中,为平均绝对误差，表示模式的气象预报误差幅度，和ME联用可以判断模式是否存在系统误差，若2个数值较为接近时说明系统误差较小，另外当ME为正值时表示预报数据偏大，反之预报模式偏小；

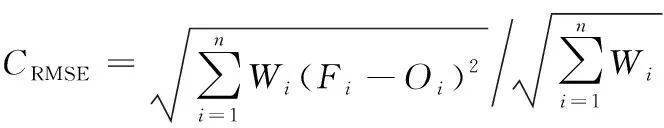
(12)

式中:为均方根误差，表示模式误差的大小，和MAE联用可以判断模式中是否存在大误差，若两个数值相近时，模式的误差相对均匀，反之具有一定的不稳定性。

(13)

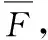
4 数据分析

在本节当中对比所用的实测气象资料为国家高空定时观测资料(T213 L31)，时间间隔为6 h，垂直方向上在规定的定压层(1 000 hPa、925 hPa、850 hPa、700 hPa、500 hPa、400 hPa、300 hPa、250 hPa、200 hPa、150 hPa、100 hPa、70 hPa)测得气象观测资料。

将WRF模式前处理后的数据与我国东北地区秋季的高空定时观测资料进行研究，主要从气压、虚温、风速和风向4个方面进行分析研究，作出图1—图4。

通过图1—图4可以直观地看出气压和虚温的计算精准度较高，风速和风向计算的数据存在着一定差异，因此需要采用3.2节中方法对误差进行分析。

图1 WRF前处理后气压数据曲线Fig.1 Comparison of atmospheric pressure data after WRF pre-processing

图2 WRF前处理后虚温数据曲线Fig.2 Comparison of virtual temperature data after WRF pre-processing

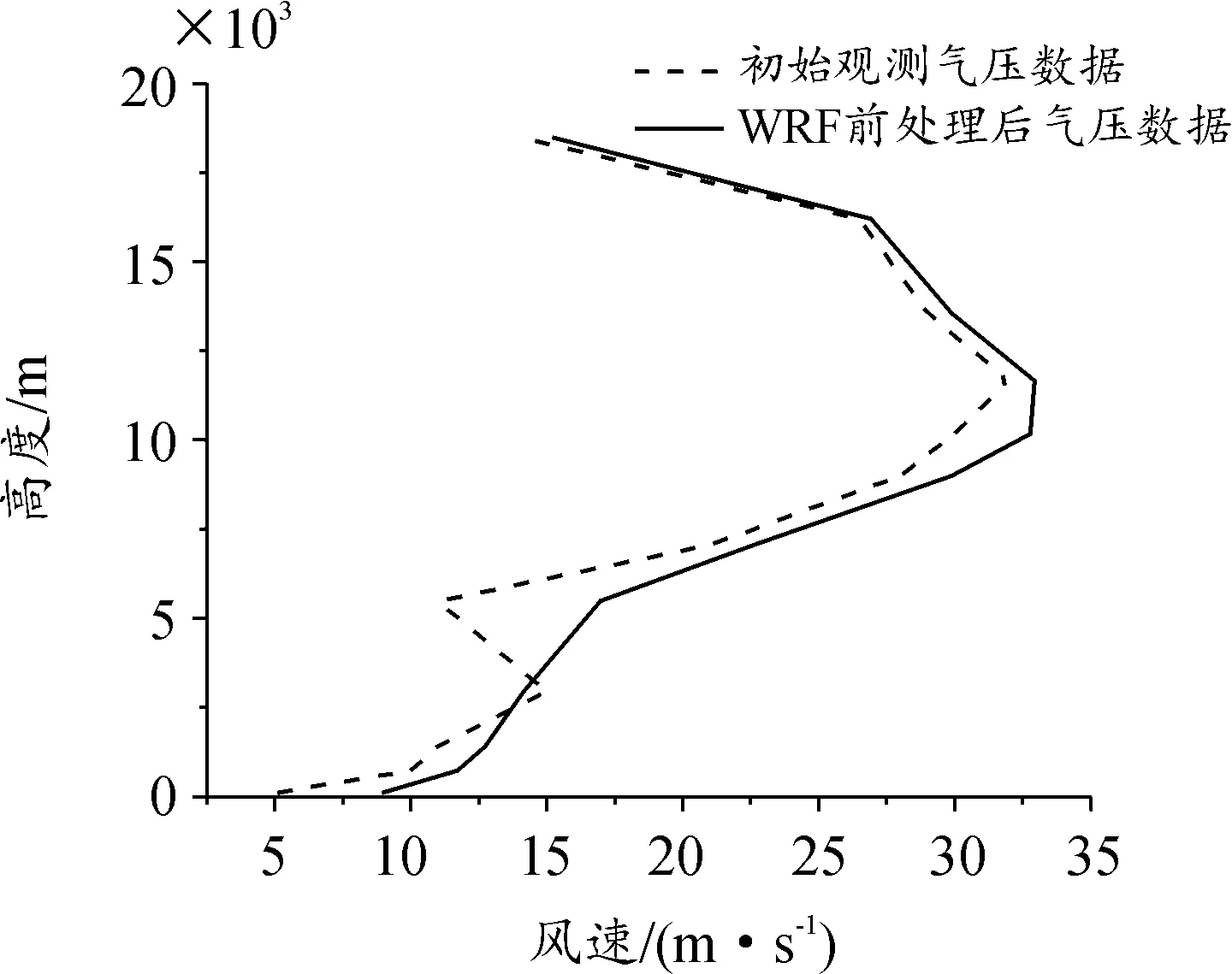
图3 WRF前处理后风速数据曲线Fig.3 Comparison of wind speed data after WRF pre-processing

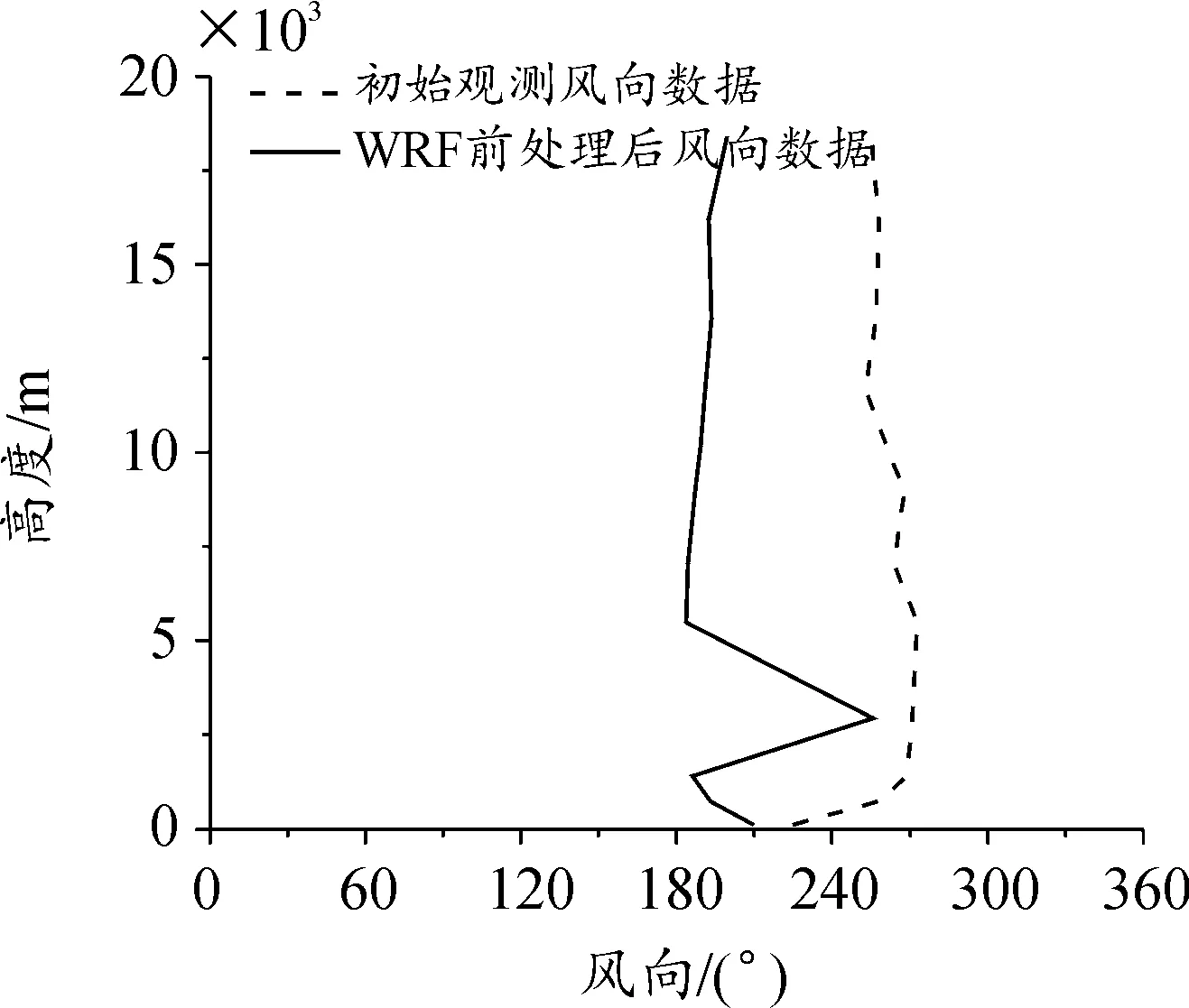
图4 WRF前处理后风向数据曲线Fig.3 Comparison of wind direction data after WRF pre-processing

之后根据外弹道计算的需求，将对气压、虚温、风速、风向4个条件在一段时间内连续进行分析，分别计算了各个气象条件的平均误差(ME)、平均绝对误差(MAE)、均方根误差(RMSE)如图5～图8所示。

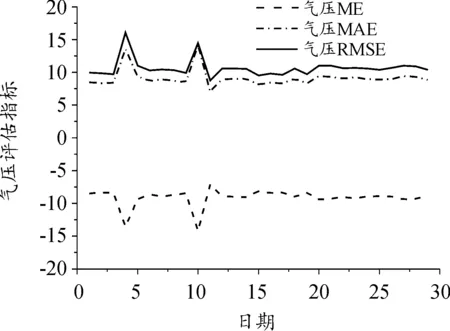
图5 气压条件的初始场误差评估参数曲线Fig.5 Initial field error evaluation parameters for atmospheric pressure conditions

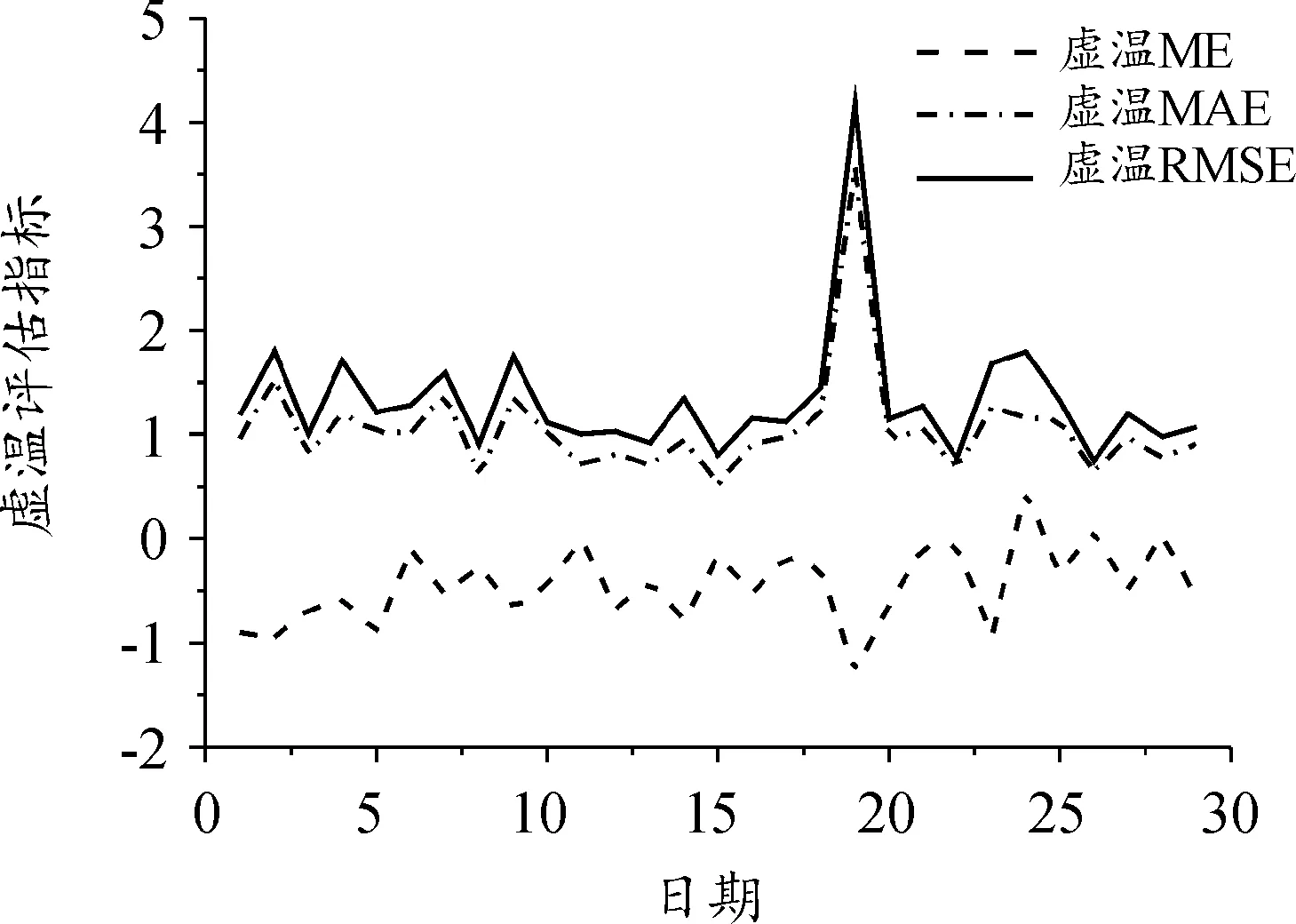
图6 虚温条件的初始场误差评估参数曲线Fig.6 Initial field error evaluation parameters for virtual temperature conditions

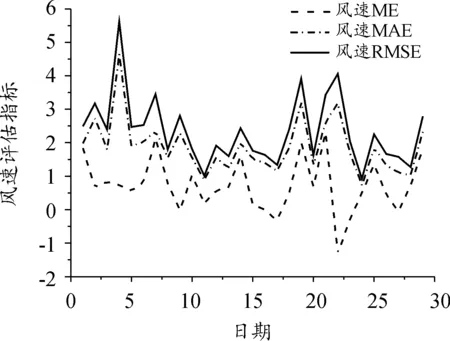
图7 风速条件的初始场误差评估参数曲线Fig.7 Initial field error evaluation parameters for wind speed conditions

图8 风向条件的初始场误差评估参数曲线Fig.8 Initial field error evaluation parameters for wind direction conditions

首先从图5～图8中4种气象诸元条件的MAE和RMSE的趋势可以看出这2个指标的相关性强，说明误差分布相对均匀，因此可以对其中每一种气象诸元进行修正。其次，对于每种气象诸元ME和MAE的值可以分析得到，如图5、图6所示，气压条件和虚温条件的ME值多为负数，说明通过WRF模式进行前处理过后的气压和虚温条件普遍为负偏差；相反，如图7所示，风速普遍存在正偏差。而如图8所示，风向条件误差每日的差别较大，相对不稳定，修正较为复杂。另外，根据RMSE的值可以对气象诸元条件进行修正，通过加权计算得到气压的RMSE均值为10.30，虚温的RMSE均值为1.23,风速的RMSE均值为2.10，风向的RMSE均值为60.52。由此可见通过WRF模式前处理后的数值气象数据，气压、虚温和风速的偏差较小，风向的偏差相对较大且相对不稳定。如图9所示，通过对相关系数的计算同样证明了该结果。

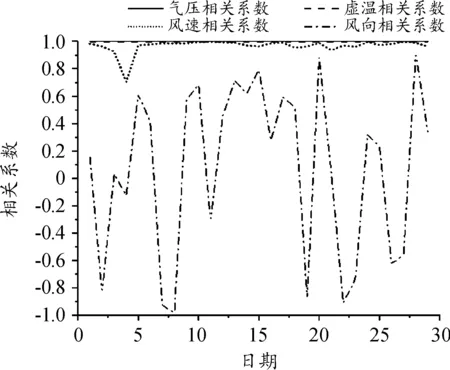
图9 WRF模式前处理后的气象诸元条件与实测气象诸元条件的相关系数曲线Fig.9 Correlation coefficients between the pre-processed meteorological conditions in the WRF model and the measured meteorological conditions

由图9可见，气压、虚温和风速3种气象诸元的相关系数都趋近于1，且均为正相关，说明了WRF模式前处理后的数据与当日的实测数据相关性强，容易修正。而风向的相关性系数波动很大，随机性大，不宜直接修正。

虽然经过WRF模式前处理后的风向条件误差值大，但平均绝对误差和均方根误差趋势较为吻合，说明可以对风向条件进行修正。本研究当中将实测气象数据当中的风速和风向分解为横风和纵风两个矢量风，并将WRF模式前处理输出的2种矢量风与当月实测气象数据分解后的2种矢量风进行对比，计算2种矢量风的平均误差(ME)、平均绝对误差(MAE)和均方根误差(RMSE)如图10、图11所示。

图10 横风的初始场误差评估参数曲线Fig.10 Initial field error evaluation parameter for cross wind

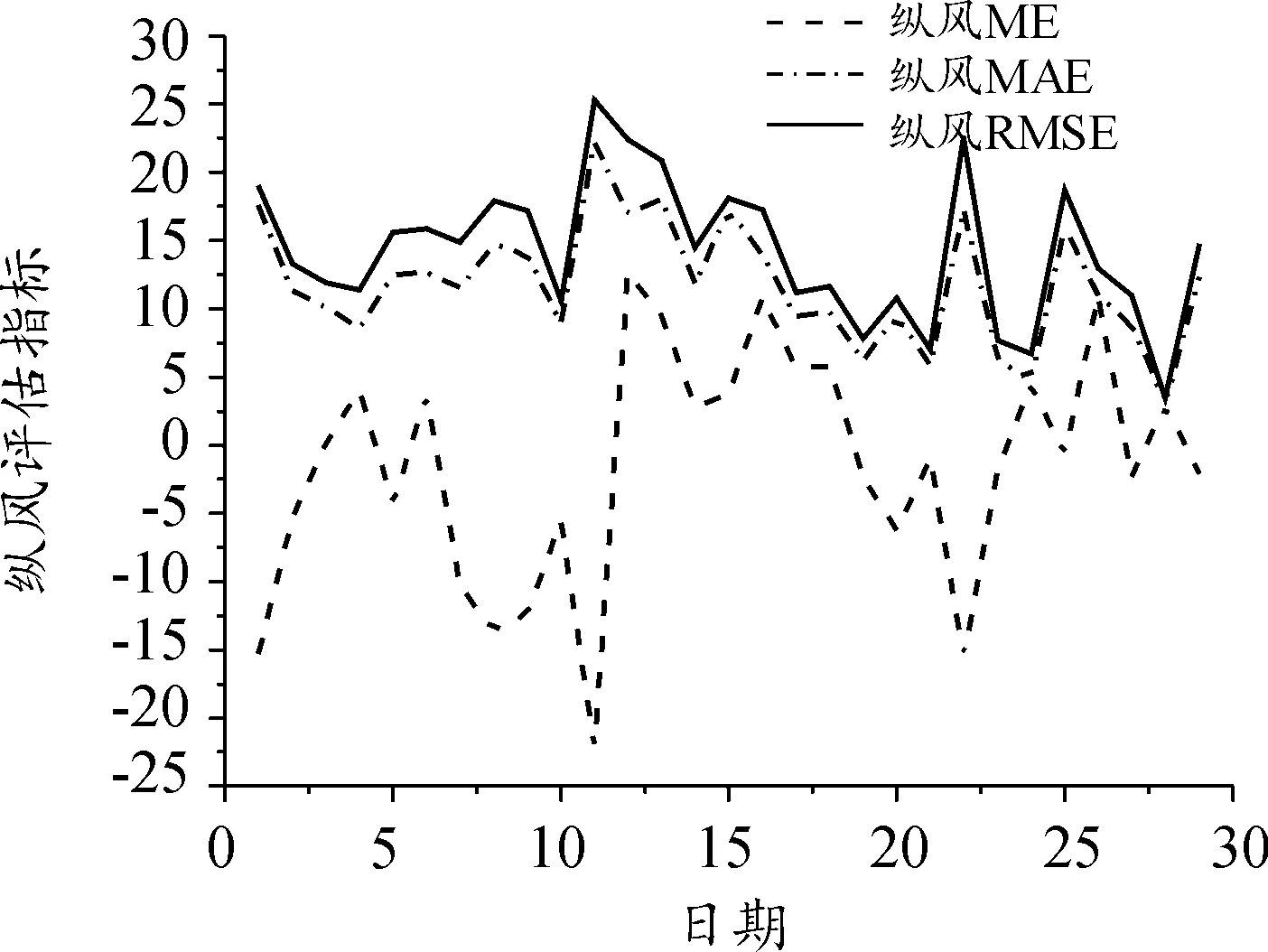
图11 纵风的初始场误差评估参数曲线Fig.11 Initial field error evaluation parameter for vertical wind

可以看出，将风速和风向2种气象条件转换为横风和纵风之后，3种评估用误差值均有明显减小和稳定，2种矢量风的均方根均值分别下降到13.91和14.21，这说明采用矢量风分解再进行修正的方法可以减小初始场误差修正的难度。

以某型榴弹炮为例，在初速930 m/s、射角51°、射向0°的炮射条件下，将WRF模式前处理后气象条件下的弹道与实测气象条件下的弹道分别进行仿真计算，得到如图12所示的弹道仿真曲线。

图12 弹道仿真曲线Fig.12 Ballistic simulation curve

5 结论

1) 本文利用WRF模式探究了以该模式作为数值天气预报初始场误差的误差值，并采用WRF模式进行前处理解算后的数值气象数据进行外弹道气象诸元转换，将得到的外弹道气象诸元数据与当日的实测气象数据进行对比，计算出平均误差、平均绝对误差、均方根误差和相关系数4个评价指标进行分析。

2) 通过分析得到：气压的RMSE值为10.30，虚温的RMSE值为1.23，风速的RMSE值为2.10，风向的RMSE值为60.52。对于基于WRF模式的初始场误差当中，气压、虚温、风速的值可以直接根据误差量进行修正。

3) 如果对风向的误差进行修正，需要进一步矢量分解，经过分解成横风和纵风的RMSE值减小到13.91、14.21，有利于后续误差修正的研究。

4) 通过一定的炮射条件得到弹道落点的平均偏差量188.02 m，射程平均偏差为170.11 m，侧偏平均偏差为80.09 m，可为后续基于WRF模式初始场误差的修正方法和修正量提供参考。