用于传感信号检测的混沌振子数值并行求解方法*

姜敏敏罗文茂赵 力

(1.南京信息职业技术学院，江苏 南京 210023；2.东南大学信息科学与工程学院，江苏 南京 210096)

近年来，将混沌理论引入信号处理领域有了较大发展，在保密通信[1]、传感信号检测[2]、信号去噪[3]、图像处理[4]等方面涌现出了众多应用成果。在应用混沌振子时，一般采用单个振子、振子阵列和耦合振子的形式。 其中，耦合振子在传感信号检测领域中有众多的研究成果，如文献[5－10]所示。 在这些文献中，普遍采用非刚性常微分方程形式的耦合混沌振子，如Lorenz 振子、Duffing 振子、Duffing-Van der Pol 振子等。 将耦合振子应用于传感信号检测的过程中，一般要进行微分方程的数值求解。随着耦合振子的增多，微分方程数量将变得庞大，所需求解运算量急剧增加。 传感信号检测的一个重要问题是求解的实时性，所以求解速度是制约耦合混沌振子应用的一个因素。

常微分方程的数值求解一般分为显式和隐式递推方法[11]。 对于刚性常微分方程一般采用隐式方法数值求解。 对于非刚性常微分方程，一般采用显式的定步长4 阶龙格库塔法进行数值求解。 采用定步长是因为变步长龙格库塔法的计算量大。 而采用4 阶精度则是因为低阶的求解精度不够，而高阶方法超出了应用的实际需求，会浪费算力。 所以采用非刚性常微分方程形式的耦合混沌振子进行传感信号检测的文献中普遍采用定步长4 阶龙格库塔法。

但是，定步长4 阶龙格库塔法的递推格式中，一个方程的求解需顺序计算4 次，运算速度较慢。 所以，提高数值计算速度是一个需要研究的问题。

半隐式递推方法在非线性问题中得到了很多研究[12－15]，但是半隐式递推格式必须根据不同非线性问题的特性来优化设计，需在稳定域、精度、计算量等方面进行考量，而没有标准算法。

针对传感信号检测时耦合混沌振子的数值求解问题，本文给出了一种半隐式的并行计算方法，其计算速度是同阶次定步长龙格库塔法的一倍。 仿真和实验证明，该方法对于常见的非刚性耦合Lorenz、Duffing 振子的求解结果与四阶龙格库塔法类似，且在实际传感信号检测任务中采用二阶方法就能得到有效结果。

1 半隐式递推格式

为了更具广泛性，考虑两个带有时间变量的2阶耦合振子，其表达式为:

式中:x、y是其中一个振子的状态变量，u、v是另一个振子的状态变量，f1、f2、g1、g2是函数，t是时间变量。

在2 阶精度时，其半隐式递推格式分为两次递推，分别为并行计算的式(2)和式(3):

式中:下标n表示第n步的数据，下标n＋1 表示第n＋1 步的数据，H为递推步长。

最终的递推结果为式(2)和式(3)的相应结果的平均值。 如变量x的第n＋1 步的递推结果xn＋1为式(2)和式(3)得到的xn＋1相加后除2，其余变量以此类推。 为了后续推导过程描述方便，将以上2 阶递推结果标记为T1(xn＋1，yn＋1，un＋1，vn＋1)。

该半隐式方法具有2 阶精度。 可以看出，式(2)中的第一、三个公式是显式递推格式，第二、四个公式是隐式递推格式。

对于式(1)所示的微分方程组，其有4个方程，如果采用定步长2 阶龙格库塔法求解，每个时间步解算4个方程，共需顺序执行2个时间步才能得到结果。 所以每次递推运算的时长是2个时间步。 式(1)如果采用以上半隐式递推算法，式(2)和式(3)可以并行计算，每次递推运算的时长是1个时间步。所以2 阶半隐式并行算法的运算速度是2 阶龙格库塔法的一倍。

对于精度要求高的情况下，需提高递推阶数。以4 阶半隐式递推格式为例，其递推分两步分别执行。

第一步的递推方法如上述式(2)、式(3)描述的2 阶方法，其递推结果为T1(xn＋1，yn＋1，un＋1，vn＋1)。

第二步的递推分为两个小步骤，第1个小步骤的递推格式如式(4)和式(5)所示:

式中:下标n＋0.5 表示第n＋0.5 步的数据，上标′表示第2 步递推的结果。

第1个小步骤的最终递推结果为式(4)和式(5)的相应结果的平均值。 如变量x的第n＋1 步的递推结果xn＋1为式(4)和式(5)得到的x′n＋0.5相加后除2，其余变量以此类推。 将以上第1个小步骤的递推结果标记为T21(xn＋0.5，yn＋0.5，un＋0.5，vn＋0.5)。

第二步的第2个小步骤的递推格式如式(6)和式(7)所示:

式中:下标n＋1 表示第n＋1 步的数据。

第2个小步骤的最终递推结果为式(6)和式(7)的相应结果的平均值。 如变量x的第n＋1 步的递推结果xn＋1为式(6)和式(7)得到的x′n＋1相加后除2，其余变量以此类推。 将以上第2个小步骤的递推结果标记为T22(xn＋1，yn＋1，un＋1，vn＋1)。

在以上的递推过程中，T1和T22的计算过程是完全独立的，可以并行计算。T1的计算是1个时间步，T22的计算需2个时间步，所以其计算时长是2个时间步。 作为对比，定步长4 阶龙格库塔法的计算需要顺序执行4个时间步。 所以，在4 阶精度下，本文方法的计算速度是定步长4 阶龙格库塔法的一倍。

以上是2 阶和4 阶的半隐式递推方法，对于更高阶的递推方法也可以类似构造。 另外，如果微分方程组的方程个数大于4，其递推格式也可以类似构造，一般要求隐式和显式格式数量相等。

2 仿真研究

2.1 耦合Lorenz 振子

Lorenz 振子作为一种常见的混沌振子，其应用非常广泛。 文献[16]提出一种非刚性耦合Lorenz振子系统，其表达式如下所示:

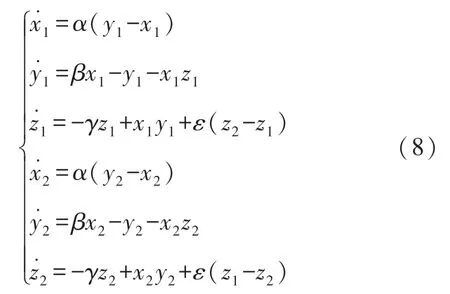
式中:x1、y1、z1是其中一个振子的状态变量，x2、y2、z2是另一个振子的状态变量，α＝10，β＝24.76，γ＝8/3，ε＝0.05。 在仿真中设定递推步长H＝0.01，递推10 000个点。

通过定步长4 阶龙格库塔法和4 阶半隐式方法计算，得到的相图分别如图1 和图2 所示。 通过对比可以看出，两种方法得到的相图是一致的，说明本文方法对于非刚性耦合Lorenz 振子的计算是精确的。

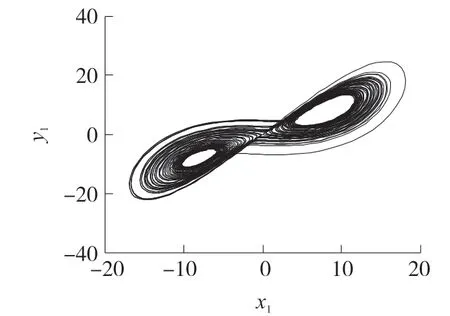
图1 龙格库塔法的相图

图2 半隐式法的相图

为了进一步对比计算精度，将两种方法对于变量x1的计算结果在不同的递推点处进行逐点对比，其结果如表1 所示。 通过对比可以看出两种方法在小数第8 位上有细小的差异，说明本文的半隐式方法在应对一般问题时具有足够的精度。

表1 计算结果对比

2.2 耦合Duffing 振子

Duffing 振子目前在传感信号检测领域应用非常广泛。 为了检测脉冲信号，文献[6]提出一种非刚性耦合Duffing 振子系统，其表达式如下所示:

式中:x1是其中一个振子的状态变量，x2是另一个振子的状态变量，s(t)为待检测信号，n(t)为噪声，F＝0.2，ω＝5×106，k＝10，ξ＝0.7，计算步长1 ns。

将以上表达式改写为1 阶微分方程组形式:

为了验证该耦合振子对脉冲信号的检测能力，仿真了一些叠加高斯白噪声的方波信号，其波形如图3(a)所示。 将该信号加入式(10)所示的耦合Duffing振子中，通过定步长4 阶龙格库塔法求解得到的结果(̇x1－̇x2)如图3(b)所示。 同样利用4 阶半隐式方法求解，得到的结果如图4(a)所示。 通过对比可以看出，两种方法得到的结果是一致的，说明本文方法对于非刚性耦合Duffing 振子的计算是精确的。

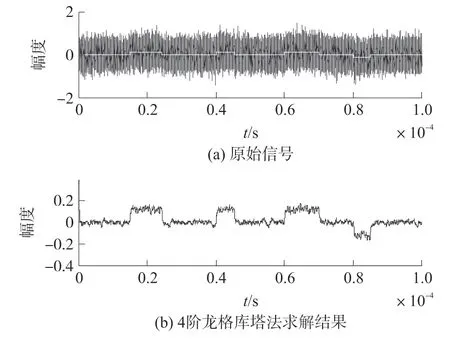
图3 龙格库塔法求解结果

图4 半隐式法求解结果

更进一步，本文探讨了2 阶精度的半隐式法对非刚性耦合混沌振子的应用可能性。 应用2 阶半隐式法对耦合Duffing 振子的求解结果如图4(b)所示。 从该图可以看出，虽然2 阶半隐式方法的求解精度不高，相比4 阶精度方法有一定的数值差异，但是落实到具体的传感信号检测应用中，可以发现2阶半隐式方法同样可以得到与4 阶方法相似的信号检测结果。 通过该算例可以得出2 阶半隐式方法可以应用于传感信号检测、可以进一步提升运算的速度的结论。

3 实验研究

为了验证本文方法在实际传感信号检测中的正确性，在高压开关柜上搭建了局部放电信号检测的实验场景。 通过带宽为300 MHz～3 GHz 的微带天线采集高频电磁信号，示波器采用LeCroy HDO9204，其带宽为2 GHz。 实验场景如图5 所示。

图5 局放信号采集场景

实验采集到的局放信号波形如图6 所示。

图6 实验采集的局放信号

将采集的局放信号输入式(9)的Duffing 振子系统，通过4 阶龙格库塔法求解，得到去噪后的输出信号如图7 所示。

从图7 可以看出，去噪后局放信号被凸显出来，说明利用Duffing 振子对局放信号能有效去噪。 同时，对比4 阶龙格库塔法和本文提出的4 阶半隐式方法对局放信号的去噪结果，可以看出两种数值求解方法得到的结果是相似的。 这说明本文半隐式方法对实际传感信号的求解也是成功的。

图7 局放信号去噪求解结果

4 结论

本文针对传感信号检测所用非刚性耦合混沌振子给出了一种半隐式并行数值算法，该算法的计算速度是相同阶数龙格库塔法的一倍。 通过耦合Lorenz 振子和耦合Duffing 振子的算例，证明了本文方法和相同阶数龙格库塔法的求解精度是相似的。并且通过算例发现，在利用耦合混沌振子进行传感信号检测的应用中，2 阶半隐式方法也能得到很好的求解结果。 因此，将耦合混沌振子应用于传感信号检测时可以尝试应用2 阶半隐式方法求解，这样可以实现更小的计算代价和更高的求解速度。 此外，局放信号的检测实验结果也表明了本文方法可以用于实际的传感信号检测环境。