基于光纤布拉格光栅的飞机装配应变检测
刘佳伟,朱永凯,徐 铭,苗 慧,王海涛
(南京航空航天大学 自动化学院,南京 210016)
0 引言
飞机装配是航空制造的重要环节,是保证飞机品质与飞行安全的关键。其流程操作极为繁琐,精度要求标准极高,故在保证装配精度的情况下进行装配所需时间较长,工作量也极大,约占飞机总工作量的50%[1-3]。装配过程中需使用装配型架对装配体进行固定与定位来保证工装质量,限制工装过程中形变与位移的产生[4-5]。期间难免会因装配人员操作失误与装配工艺的缺陷等一系列的问题而产生装配应力,这样的应力可能会导致装配体进行装配的关键位置产生偏差,这些偏差会直接影响到飞机的质量,降低飞机工作的稳定性。故装配过程中的应变监测对于整个装配环节来说极为重要。
目前,随着检测技术的不断革新,国内外学者将各种检测技术运用到工装过程中。波音公司将室内GPS测量系统运用到飞机装配中,提高了装配效率[6]。Marguet等提出一种将激光技术、视觉测量、计算机辅助测量、最佳匹配优化软件结合的装配方法,从而实现装配过程飞机组件状态的监测[7]。P.Vichare等监测了飞机装配过程中的信息,以此预测飞机组件在装配过程的尺寸变化[8]。Saadat等提出了一种基于有限元的表格预测法,来对飞机零部件装配中机翼肋条组件的尺寸变化进行预测,其预测结果与实验结果误差在1 mm之内[9]。西北工业大学田锡天等通过装配组件的工艺分析及实验数据,搭建了飞机装配精度模型,实现了对飞机机身壁板的装配质量控制[10]。
针对应变检测来说,传统的应变检测方法大致分为两种,分别为非接触式与接触式,其中非接触式主要有CCD摄像法、激光扫描法与数字图像相关方法等[11-14]。这种方法的原理是基于相机所拍摄的图片或者经物体反射所收集的光信号来进行应变特征提取。其本身结构较为复杂且所需检测设备较多,并且在获取特征的过程中,由于复杂的工装型架结构、工装定位器以及装配人员与设备的遮挡,会导致很多所需的装配体关键部位的特征信号无法被获取。此外,在大型飞行器的工装现场,非接触式测量法需要使用拼接匹配技术才能够实现整体测量,监测的难度较大。接触式的典型方法有电阻应变片法[15],其原理是将感知的应变信号转换成电信号,经过硬件将电信号进行放大最后经过信号处理得到应变信息。其可以直接粘贴于装配体表面,不受型架结构等遮挡,无需大量的检测设备就可以直观的测得所需关键部位的应变状态。但是电阻应变片法受外界环境与安装手法影响较大[16-18],而FBG传感器的抗干扰能力强、测量精度高、体积小、质量轻,可以较好的满足装配需求[19-21],故选择FBG进行飞机装配过程中的应变检测。
本文利用监测装配过程中FBG传感器的中心波长变化的方式来实现装配体局部应变的检测,设计了布设方案,标定了传感器灵敏度,并且针对所得数据提出一种基于改进的EEMD与SSA的应变信号提取算法,从而实现装配过程中装配体的局部应变监测。
1 FBG检测原理
光纤光栅是一种折射率轴向周期性调制而产生的衍射光栅,其具有稳定性好、耐腐蚀性好、体积小、质量轻、灵敏度高、抗电磁干扰等优点。而光纤布拉格光栅(FBG)是光纤光栅极为重要的组成部分之一,其一般通过紫外光照射等工艺来改变单模裸光纤的性质,使部分光纤纤芯的折射率形成周期性的调制,从而形成一小段相位光栅。光纤布拉格光栅对光有选择作用,主要体现在对光的波长大小进行选择,只有符合条件的固定波段的波长会被反射,其余波长的光则会正常通过光纤布拉格光栅。当应变振动等物理量产生时,会使光栅折射率产生周期性改变,导致反射波段的整体偏移,最终根据变化量实现对应变等物理量的检测。其原理如图1所示。

图1 FBG工作原理图
FBG的反射谱的中心波长为:
λB=2neffΛ
(1)
式中,λB为FBG的反射谱中心波长,neff为纤芯的反向耦合有效折射率,Λ为光栅周期。当应变、温度、振动等物理量作用于FBG时,从而导致光栅周期及有效折射率的变化,最终使得FBG的反射谱中心波长产生漂移,通过测量漂移量,即可实现外界物理量的测量。
FBG传感器主要对应变和温度敏感,利用FBG传感器对大部分物理量的测量都是通过检测应变来间接实现的,如位移、压力、变形、振动的测量等(温度除外)。假设光纤光栅受轴向作用力时,且温度场保持恒定,从微观上分析应变和FBG中心波长的关系。
应变对FBG中心波长的影响包含两个方面,一个是由于弹性力作用使得光栅周期发生改变,另一个是由于光纤的弹光效应引起FBG有效折射率的变化。
其中,根据胡克定律,应变带来的光栅周期Λ的变化为:
ΔΛ=ΛεZ
(2)
εZ为轴向应变。
弹光效应引起的有效折射率的变化为:
(3)
定义有效弹光系数:
(4)
Pij是弹光系数,v是纤芯材料的泊松比。
综合上式,得到仅受轴向应力时光纤光栅中心波长变化的表达式为:
(5)
显然,当FBG仅受轴向应力时,其中心波长变化量和轴向应变成正比关系。
另外,当光纤光栅受到径向压力时,光谱也会发生细微变化。早期研究人员直接对裸光纤光栅进行横向应变测量,发现对其施加横向力时,光路返回光谱的波峰变化极其微弱,很难运用于传感领域。因此,在实际的工程应用中,由径向应变产生的影响可忽略不计。
2 飞机装配应变检测系统设计
2.1 装配实验系统
为了实现关键部位装配应变的检测,首先要选取合适的监测点。飞机工装定位器可以保证飞机装配的质量与精度,其在装配过程中由于人工、机器或零件自身的问题,可能会产生强迫装配等现象,导致工装定位器产生应变,为了判断这种应变是否在装配允许产生的应变量范围之内,需要对工装定位器的具体应变量进行监测。因此在5个工装定位器上设置5个测量点,在测量点上粘贴传统的应变片传感器与光纤光栅传感器,并且在每个定位器附近位置依次进行装配,测量装配时定位器上布设的FBG传感器所产生的应变量。所用布拉格光纤光栅中心波长1 555 nm、栅区长度为10 mm,装配型架材料为钢材,机翼材料为碳纤维增强复合材料。因为机翼在装配时,需要先用工艺螺钉夹紧,装配点附近受到装配影响最大,为了得到机翼装配时的机翼形变特性,故实验中将FBG布置在距装配点2 mm处。实验首先用胶带将FBG粘贴在测量点,从而起到固定光栅的作用。随后选用硬度、杨氏模量等参数合适的聚合物胶水均匀涂覆光栅部分,起到聚合物增敏的作用。其中装配体测量点需提前进行打磨并用酒精擦拭,使其表面光滑洁净,这样可以使FBG工作更加稳定。光纤光栅解调仪为Micro-Optics公司的SM130,其解调频率为1 kHz。测试中按照安装时间顺序依次对5个装配点进行装配。

图2 装配实验系统示意图
2.2 FBG的标定
在与装配体局部应变测量相同的环境下进行FBG标定,以此来避免温度与湿度对传感器的影响。将FBG用与上一部分相同的手法粘贴于等强度板材之上对其进行应力加载实验,当波长变化量从0.01 nm增加至0.2 nm时,对应应变量从13 με增至560 με,计算得FBG传感器测量应变的灵敏度为0.35 pm/με,拟合方程线性度高于0.99,效果较好。其中FBG中心波长变化量与应力变化的特征如图3所示。

图3 中心波长变化量随应变变化特征图
2.3 原始数据分析
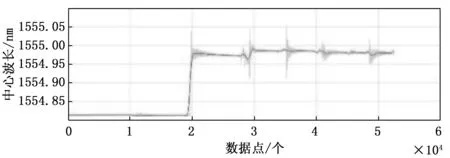
以测量点1上的FBG传感器为例,其实验原始数据如图4所示,在初始状态下信号平稳,但是携带噪声,中心波长值约为1 554.81 nm,并且可以明显看出5个装配位置进行装配时对FBG的中心波长产生了影响,但是中心波长除了受应变的影响外,还被冲击与振动影响,故需要对信号进行解耦,从而剔除掉出应变外的信号。
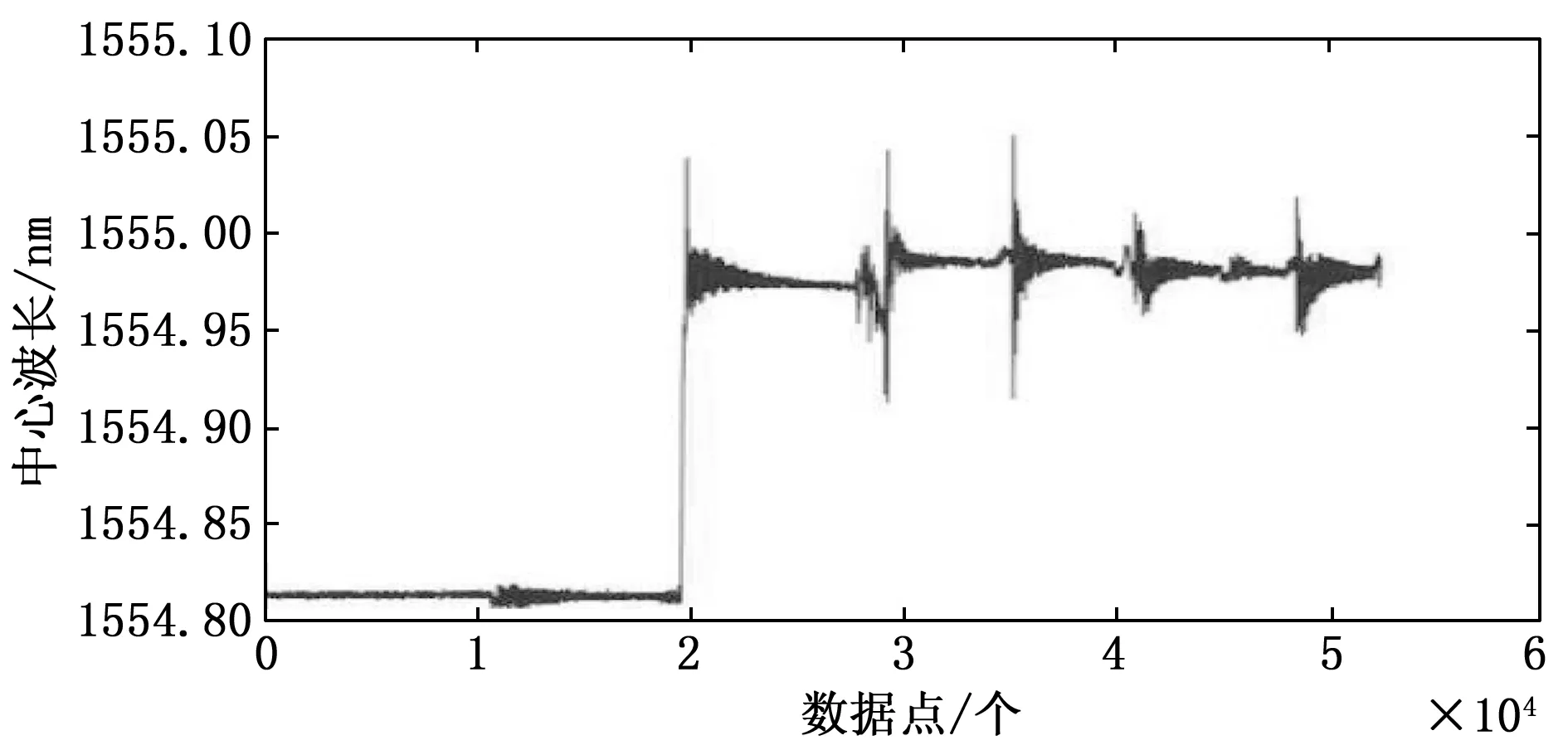
图4 原始中心波长信号图
3 应变提取算法设计
3.1 设计目的
整个装配过程中所采集的信号由光纤光栅解调仪自带的背景噪声、应变信号、冲击信号、振动信号与其他噪声信号组成。而本文所需的为装配体的应变信息,故设计一种算法对解调后的原始信号进行处理,从而实现应变的提取。
在装配应变检测实验中,因为应变、冲击、振动等信号的频率特征不同,所以可以依次进行应变的提取。最常用的频域分析方法为傅里叶变换,但是傅里叶变换仅适用于平稳信号,而针对非平稳信号具有较大局限性,其只能获取信号中包含哪些频率成分,无法得到每个频率成分出现的时域信息,因此不能识别装配体实时的状态。虽然目前已有改进的短时傅里叶变换,可以进行“加窗”的方式对时域进行等长划分,其窗口窄时,时间分辨率较高,但是频率分辨率较低;其窗口宽时,频率分辨率较高,然而时间分辨率较低。又因为高频的信号成分适合小窗口,低频的信号成分适合大窗口,所以短时傅里叶变换难以满足飞机装配应变的测量需求。
小波变换是针对傅里叶变换的不足而发展的来的时频分析方法,其将傅里叶变换所使用的无限长的三角函数基替换为有限长可以变化的基函数。当对高频信号进行分析时,小波的基函数会产生收缩;当对低频信号进行分析时,小波的基函数会产生伸展,所以可以保证对信号进行处理时同时具备较高的时间与频率分辨率。但是小波的基函数对整个信号分析的影响极大,其被确定后在整个信号处理的过程中无法被更换,缺乏适应性,对局部的特征提取可能不够准确。而经验模态(EMD)分解与小波分析理论上都可以精确提取出频率随时间变化的规律,但是EMD分解基于信号本身的极值点分布,不需要选择基函数,更适用于非线性非平稳的信号。因此将EMD分解进行一些改进来对装配应变信号进行提取。
3.2 EMD与EEMD算法
经验模态(EMD)分解与小波分析理论上都可以精确提取出频率随时间变化的规律,但是EMD分解基于信号本身的极值点分布,不需要选择基函数,更适用于非线性非平稳的信号。其原理可以简单阐释为一个信号筛选的过程,将原始信号基于自身的局部特征尺度,从低频到高频进行自适应分解,得到多个本征模态函数(IMF)分量及一个残余分量。每个IMF分量需满足两个条件:
1)对于任意IMF分量,极值点的个数和过零点的个数相等或至多相差一个;
2)使用三次样条函数连接的,由局部极大值点和局部极小值点分别形成的上下包络线的均值为零。
筛选出第一个IMF分量后,通过从原始的信号中减去筛选出来的IMF分量,并重复上述过程进而获得下一个IMF分量,当信号的残差中包含不超过两个极值时停止筛选。
虽然EMD分解具备自适应性与完备性等有点,但是其仍会存在模态混叠、拟合过冲、末端效应等缺陷。为了弥补这些缺陷,故引入集合经验模态(EEMD)分解,利用白噪声的频谱是均匀分布的特性,将白噪声引入所分析的信号,其会使得信号自适应分布到合适的参考尺度上,又因为白噪声具有均值为零的特点,经过多次平均之后对于每个点来说即可抵消噪声的影响。最终得到各个频段的信号。
3.3 SSA算法
SSA是一种用于处理非线性时间序列数据的方法,通过对所要研究的时间序列的轨迹矩阵进行分解、重构等操作,提取出时间序列中的不同成分序列。
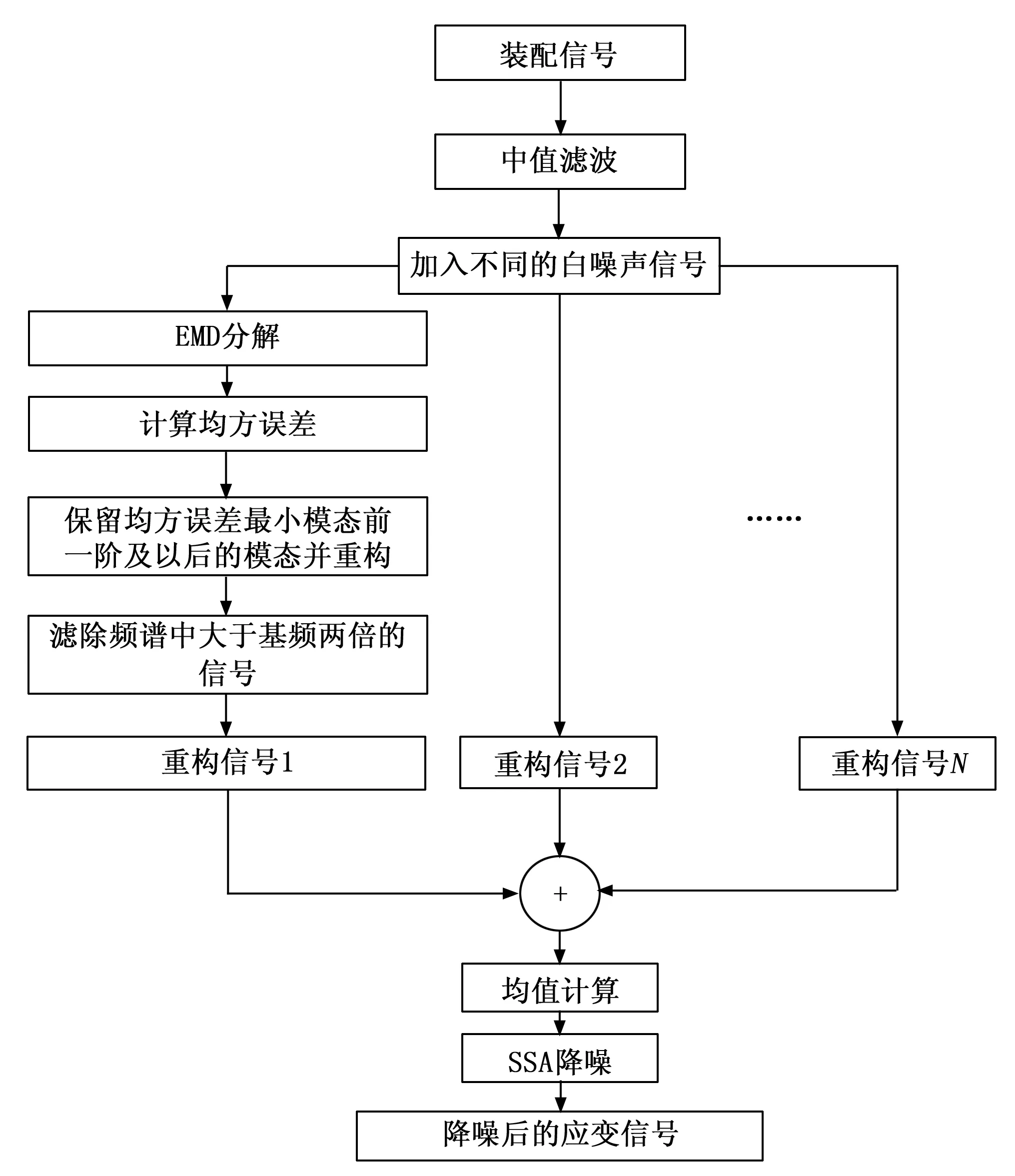
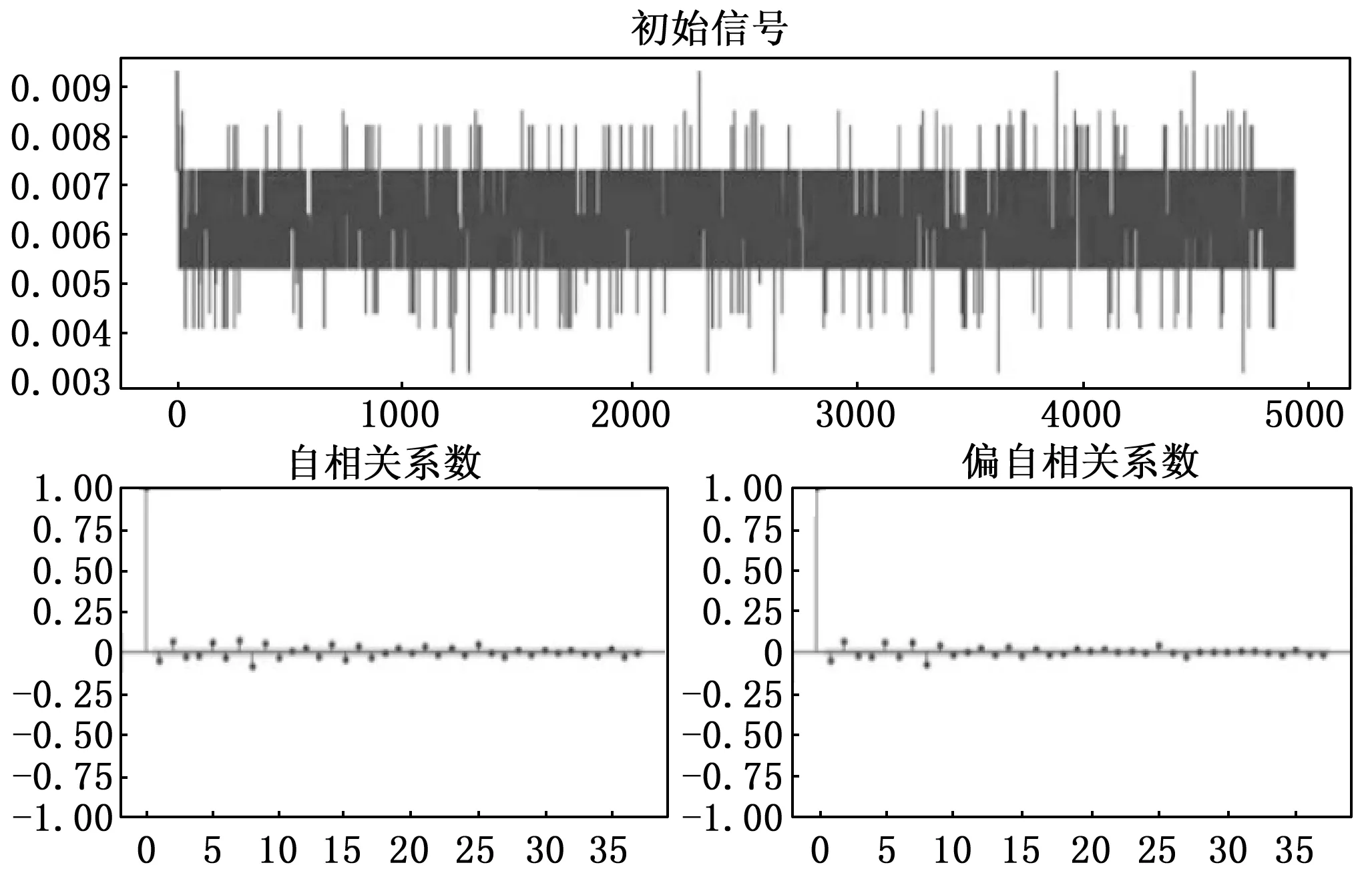
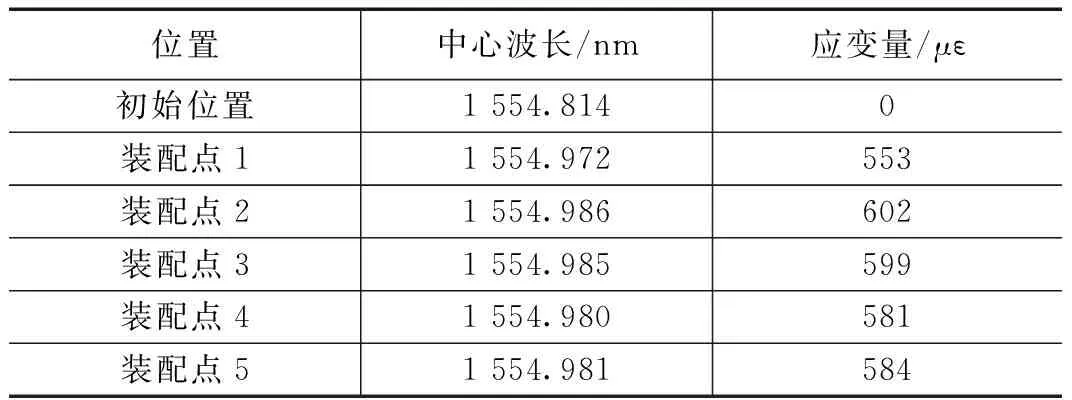
将给定的非线性信号视为一维时间序列[x1,x2,…,xN],并且给定窗口的长度为L(L (6) 因为直接对轨迹矩阵进行分解的难度较大,故取轨迹矩阵的协方差矩阵进行分解,令协方差矩阵为S: S=XXT (7) 随后对S进行特征值分解得到L个特征值λ1>λ2>…>λL≥0,以及这些特征值对应的特征向量E1,E2,…,EL,这些特征向量被称为经验正交函数。其中奇异值大小表示信号与噪声的能量大小关系,奇异值较大的点为信号点,则奇异值较小的点为噪声。接下来计算机翼的装配应变信号在特征向量上的投影: 0≤i≤N-L,i=1,2,…,m (8) (9) 取重构信号中的前面能量值大的信号即可实现应变信号的提取。 针对装配应变的提取将EEMD分解进行改进,对噪声信号进行滤除并且尽可能保留有效信号。在此基础上继续引入奇异谱分析(SSA)方法,对改进EEMD分解之后的应变信号进行分解,分解后会产生较大特征值的有效信号与较小特征值的噪声信号,保留大特征值分量即可实现降噪的目的,算法流程图5所示。 图5 算法流程图 首先对原始信号进行处理,因为背景噪声是加性噪声,选择中值滤波将其进行剔除。随后将具有标准正态分布的白噪声ni(t)叠加进原始信号a(t),从而获得新的信号ai(t),其中ai(t)=a(t)+ni(t)。取加入的信号数量为10个,则i=1,2,…,10。将这10个含正态分布噪声的信号xi(t)分别进行EMD分解就会分别得到若干个所需的IMF分量,进行重构后,即获得信号xi(t),i=1,2,…,10。在每个信号分解出的分量中,所需要的工装应变信号主要在低频的IMF中体现出来,而噪声信号主要包含在最先获得的一个或者几个高频的IMF中。其中一般认为存在某分量为噪声与应变信号的分界线。因此将分量从IMFi- IMFn进行叠加,i=1,2,…,10。并对叠加后连续的每两个信号求其均方误差。其中均方误差最小值即为分界点,但是由于装配时信号的频率可能相差并不是特别明显,最小值前一阶模态可能仍含有一些有效信号,故将分界点前提,保留最小值出现前的一个模态与其后续模态,舍弃最小值前两阶及更前的信号。为了进一步保留有效信号并消除上一步最小值前一阶中所包含的噪声信号,需对剩下的模态进行处理。通常情况下,噪声信号的频率远大于基波信号的频率,通过傅里叶变换,获得每个IMF分量的频谱,根据工装信号的特征,将频谱中幅值最高的频率作为基频,设置基频的两倍作为参考点,使用巴特沃斯型低通滤波将IMF分量中频率超出该参考点的信号滤除,最后整合为去噪后的函数。 利用白噪声均值为0的特性,将上述10个整合后的重构信号进行均值计算,得出经过改进的EEMD分解后的最终信号,即: (10) 由于解调仪会自带噪声信号,因此需要首先对噪声进行分析与剔除,为了分析解调设备自身存在的噪声,将一根光纤光栅进行固定,保持其中心波长的稳定在初始值,这样接入解调设备后,所得信号仅为初始值与噪声信号,不包含其他可能引起中心波长漂移的信号。初始信号的时域与频域信息如图6所示,可以从中看出其特征与白噪声信号相似。 图6 初始信号时域与频域信息 为了验证该信号是否为白噪声,可以使用求自相关函数的方法进行判断。一个纯白噪声信号具有纯随机性,代表其信号各项之间没有相关关系,即各项的自相关系数为0。但是该情况是只会在理论上出现的理想情况,由于实际中信号序列的有限性,信号序列的自相关系数不可能为0,并且本次检验的信号为解调仪的初始信号,除固有噪声外仍可能受其他外界物理量的微弱影响,因此其自相关系数如果满足第0项为1,其他项中大部分接近于0即可认为信号主要由白噪声组成。初始信号的自相关系数与偏自相关系数如图7所示,可以看出该信号符合白噪声的自相关系数与偏自相关系数分布,故认为解调仪的固有噪声为白噪声信号。白噪声虽然具有较强的随机性,但是其在某一段区间内存在均值为0的特性。因此可以通过对初始信号求中值的方法来进行滤波处理取滤除解调仪本身固有噪声后的信号的进行EEMD分解,其分解后的各阶IMF分量及残差信号如图8所示。 图7 初始信号的自相关系数与偏自相关系数分布图 图8 各阶IMF分量及残差信号 分解的结果如下式: (11) 其中:cj(t)代表了各种IMF分量,r(t)是最终的残余分量,对于装配应变实验中的信号来说,应变为低频信号,冲击与振动为高频信号,而IMF分量具有从高频到低频分布的特点,一般认为存在着某一阶分量,其之前的分量由冲击与振动这类高频信号主导,而其后面的分量由应变导致的低频信号主导。因此采用计算连续两个重构信号的均方误差的方式来决定高频与低频的分界点。其极小值就认为是分界点,均方误差数值如图9所示,由图可见,均方误差最小值出现在第七阶模态中,故取第六阶至最后一阶模态作为有效信号,进行频谱分析,并使用巴特沃斯滤波器将大于基频两倍的信号滤除后,进行整合,即可提取有效的应变值。经过改进算法处理的信号与普通EMD分解的信号对比如图10所示,可以明显观察到普通EMD分解后的信号忽略掉了原始信号中的许多较小的应变信息,其原因是对于被认为是噪声的模态,普通EMD分解会将其直接剔除,其包含的许多有用的信息也相应的被剔除,而经过改进后的算法则明显更贴合原始信号的应变趋势,保留了更多的有效信息。 图9 均方误差数值图 图10 算法对比图 经过改进后的算法虽然较普通EMD分解来说效果已有较大提升,然而其仍包含一些由噪声与冲击信号对其的影响,使得涌边的提取仍存在一些误差,故继续将信号进行去噪处理,将每一个经过改进算法处理后的重构信号进行均值计算,并使用SSA算法进行进一步处理。经处理后的信号如图11所示,经过均值计算与SSA降噪后的信号相比能更好地反应原始信号的变化趋势,并且曲线更为平滑,对于应变量也能更好地表征。 图11 经SSA分解后的信号图 根据算法处提取的应变信号,将工装过程中FBG的中心波长变化及其对应的装配体产生的应变量列出,以第一个FBG为例,其数据如表1所示,未开始装配时,FBG不受除解调系统自带的加性噪声之外的任何因素影响,故其初始波长保持在一个稳定的数值,中心波长为1 554.814 nm,其对应应变量为0。在第一个装配位置进行装配时,由于测点距其较近,故受到该装配位置影响最大,光栅受到冲击与应变的影响,波长迅速上升并逐渐下降,随着第一个点装配工作的完成最终稳定于1 554.972 nm,对应应变量为553 με。后4个装配点进行装配时,测点距离这些点较远,故产生的应变量较小,对应的应变量分别为602 με、599 με、581 με与584 με。在其他4个工装定位器上粘贴的光纤光栅数据与其类似,得到的数据与如表2~5所示。为了印证FBG所测应变量的准确性,故在所有装配完成后,将FBG与应变片所得应变数据进行比较。应变片1~5所测应变量分别为547 με、625 με、503 με、778 με、653 με,经计算,FBG与应变片所测应变量误差在8%以内。 表1 测量点1的应变波长对应表 表2 测量点2的应变波长对应表 表3 测量点3的应变波长对应表 表4 测量点4的应变波长对应表 表5 测量点5的应变波长对应表 本文针对飞机装配过程中装配体的局部应变监测展开了相关的研究工作。根据FBG传感器的工作原理,选择了合适的封装材料并对其应变特性进行了实验研究,实验表明封装后传感器的灵敏度为0.35 pm/;根据信号的特点设计了一种改进的EEMD与SSA相结合的信号处理算法,能够对应变信号进行提取并降噪,经过对比证明,该算法相较普通EMD分解能更好地实现有效信息的提取,更好地表征了应变量。并通过对处理后的信号进行分析,最终获取了5个装配点依次进行装配后,FBG传感器布设处所产生的应变信息,其与应变片传感器的误差在8%以内。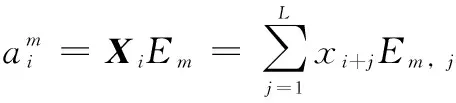
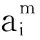
3.4 基于EEMD与SSA的算法设计
4 实验数据处理
4.1 应变信号提取




4.2 应变数据计算




5 结束语

