NiFe-YIG颗粒膜中铁磁共振线宽的角度依赖性*

韩 莹，郑博含，钟智勇

(电子科技大学 电子薄膜与集成器件国家重点实验室，成都 610054)

0 引 言

铁磁共振(FMR)线宽对基础理论研究和高频应用都有重要的意义。一般对于磁性薄膜来说，对FMR线宽的贡献包括本征效应和非本征效应，本征效应为吉尔伯特阻尼，它起源于自旋轨道弛豫和磁振子-声子的相互作用；非本征效应包括非均匀展宽、双磁子散射及镶嵌效应导致的线宽展宽，非均匀效应展宽是与频率无关的；双磁子散射效应指的是波矢为0的铁磁共振模式被激发为波矢不为0的自旋波模式，一般是由薄膜内部的短程缺陷激发；镶嵌效应则一般由长程缺陷激发[1-9]。

本文主要通过铁磁共振面外转角测试的方法来研究(Ni80Fe20)x(Y3Fe5O12)1-x颗粒薄膜的内部线宽展宽机制。通过改变外加磁场与薄膜平面的夹角，发现共振场和线宽均会发生改变，并对线宽进行分离，可进一步研究不同的YIG组分含量对颗粒薄膜线宽变化机制的影响。

1 实 验

实验中主要使用射频磁控溅射的方法来制备薄膜，采用BMS560B型高真空磁控溅射镀膜系统，采用Ni80Fe20合金靶材，并在靶材的溅射跑道上用银浆依次粘贴了1-6颗YIG贴片。由于YIG贴片的尺寸为10 mm，将所有YIG 贴片均只保留部分边缘与溅射跑道相接触，通过调整贴片位置和数量，调节薄膜内部NiFe、YIG的相对含量，成功制备出具有良好成分梯度的颗粒膜样品。实验在背底真空低于8.0×10-5Pa，Ar气溅射气压为0.5 Pa，射频功率为50 W条件下完成，在硅(100)衬底上沉积厚度为50 nm的薄膜。

本文主要通过面外转角铁磁共振对不同数量贴片条件下制备的薄膜样品进行表征(通过能谱仪(EDS)测试可知随着贴片数量由1增加至6，制备出(Ni80-Fe20)x(Y3Fe5O12)1-x薄膜(x分别为0.848、0.776、0.641、0.468、0.371、0.257)，主要使用的表征方法为Phase-FMR技术。

2 理论背景

面外转角测试数据拟合部分采用理论计算总线宽，以期计算数值与测试曲线达到最佳拟合效果；通过调整对应的拟合参数使得拟合曲线与数值曲线逼近，获取最终的拟合结果。

体系总自由能表达式为：

(1)

其中，H0为外加磁场强度，θH为外加磁场角度，θM为磁化矢量平衡角度，Ms为饱和磁化强度，Meff为有效磁化强度。

将所求得的平衡条件方程表示成以下形式：

(2)

铁磁共振频率条件[10-12]如下：

(3)

可推导出共振场Hres表达式如下：

(4)

当满足共振条件时，平衡条件方程中即有H0=Hres，通过(2)式和(4)式可得如下方程：

(5)

将人为给定的Meff、γ值以及测试中设定的外磁场转角θH值和微波频率f值带入(5)式，利用该方程求解θM的数值解。

随后将θM数值解反向带入共振场表达式(4)中，即可求得在人为设定的Meff及γ值下共振场的计算值；通过将面外转角测试的多个角度值利用上述步骤计算，可以得到设定Meff和γ条件下所有面外角度值对应的共振磁场。用理论计算得到的这一组Hres-θH值绘制曲线，观察该曲线是否与面外转角铁磁共振测试所得数据线型吻合，如偏移较大则需要调整设定的Meff和γ值，当二者相吻合时，则表示拟合成功，此时对应的Meff和γ值即为真实值。

将以上步骤中每个θH值所对应计算出该外磁场角度下发生铁磁共振时的θM数值解、以及计算得到的共振场值H0=Hres、有效磁化强度Meff值代入到磁拖曳函数[12]中：

(7)

最终求解得到随着面外转角θH值的变化，发生铁磁共振时每一个θH值对应的磁拖曳函数Ξ,当θH-θM=0时，Ξ=1[13]。在此基础上，分别计算每一部分的线宽，即可实现对总线宽的分离。

(1)吉尔伯特(Glibert)阻尼线宽项

吉尔伯特阻尼对应的线宽项即为本征线宽[12]，表达式如下：

(8)

阻尼因子α[14]还可表示为α=G/γMs，此处仅使用阻尼因子α作为唯一拟合参数进行拟合。

(2)双磁子散射(Two-magnon scattering)效应线宽项

双磁子散射效应对应的线宽展宽项表达式[15-16]如下：

(9)

该表达式中，磁拖曳函数Ξ写在分母上，是一种近似表达方法，原表达式中，磁拖曳函数Ξ写在Γ(H0,θH)函数内部[12]。在此为了保证结果偏差不大的前提下拟合更简便，即默认Γ为一常数拟合参数，此时的适用条件为：双磁子散射效应的影响强度Γ随外磁场强度及方向变化而变化的幅度较小。

(3)镶嵌效应(Mosaicity)线宽项

此处同时考虑各向异性、有效磁化强度Meff随外加磁场方向变化产生的波动进而导致的镶嵌效应对线宽展宽[19-21]的贡献。其表达式如下：

(10)

以方程中的第一项为例，共振场对外加磁场角度值θH的偏导数表达式如下：

(11)

其中，ΔθH和ΔMeff为拟合参数。

从以上讨论中可得到最终总线宽拟合公式[10-11]：

ΔH=ΔHGilbert+ΔHTMS+ΔHMosaicity+ΔHinhom

(12)

除以上讨论过的线宽成分外，还额外加入了与频率无关的磁非均匀效应导致的非均匀展宽项ΔHinhom，通过以上方法可以对线宽数据进行拟合，并根据不同的线宽机制对应的公式对总线宽进行分离。

3 结果与讨论

3.1 不同组分颗粒膜的铁磁共振表征结果

首先，对六种组分下的颗粒膜样品进行定频扫场测试，测试结果如图1(a)所示，发现在YIG掺杂含量较低时，主共振峰左侧出现了一个小的旁峰，且该峰的强度随着YIG组分含量的提升而逐渐减弱，同时该峰与主共振峰之间的间距也在逐渐缩小；该峰可能是NiFe薄膜中的涡流效应激发了垂直自旋驻波(PSSW)模式而导致的，而YIG铁氧体为绝缘体材料，随着颗粒膜样品中的绝缘物质含量逐渐增高，对涡流效应有一定的抑制作用，使得垂直自旋驻波模式逐渐消失。

该组样品无明显的面内各向异性，因此对图1(b)中共振场-频率数据进行拟合时，可忽略面内单轴各向异性场的影响，利用简化后的Kittel公式进行拟合：

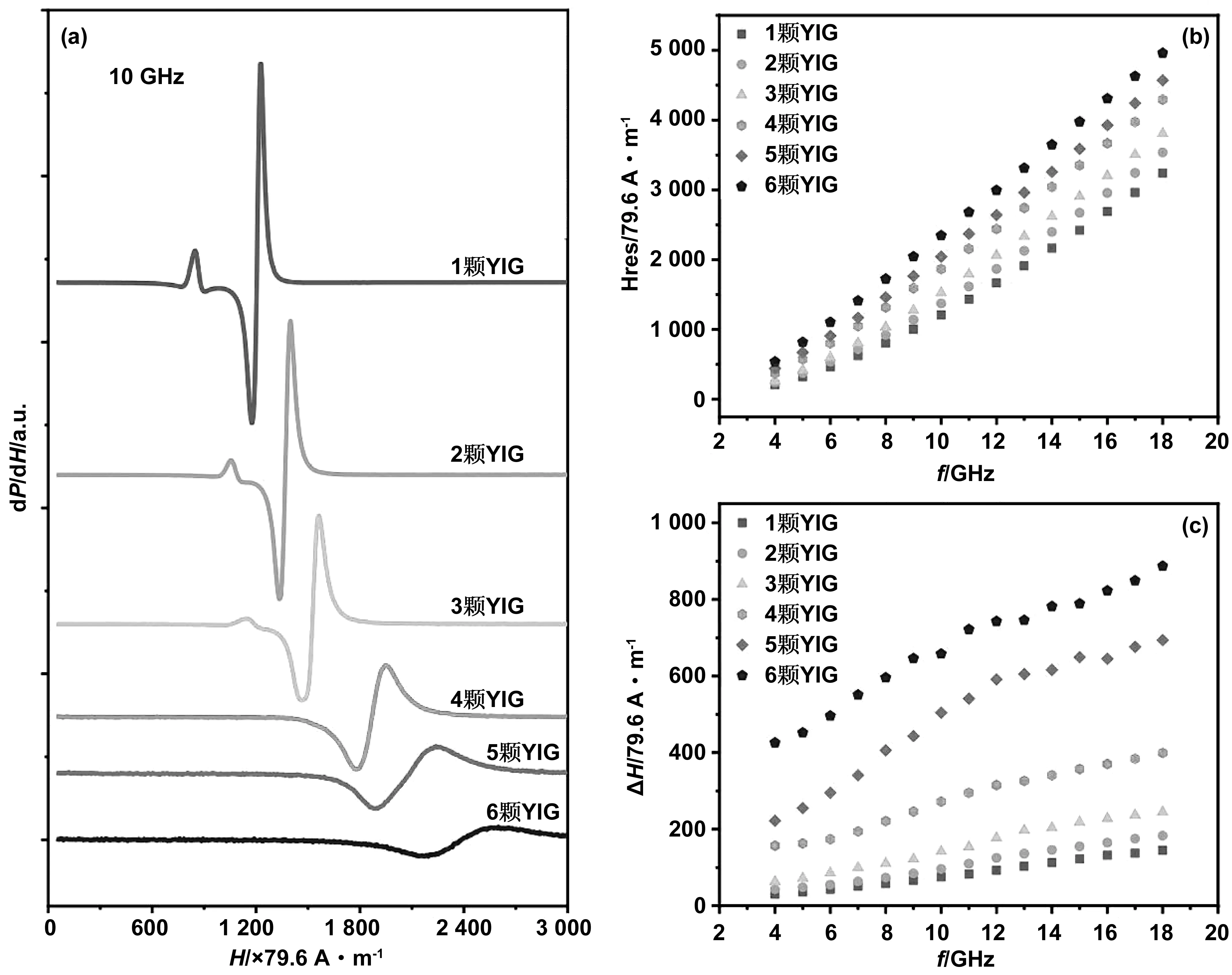
图1 不同组分下50 nm厚(Ni80Fe20)x(Y3Fe5O12)1-x薄膜的Phase-FMR扫场法测试 (a)10 GHz下随组分变化的铁磁共振峰曲线 (b)6种组分颗粒膜的变频点测试Hres-f数据 (c)6种组分颗粒膜的变频点测试△H-f数据Fig 1 Phase-FMR sweep field test of 50 nm thick (Ni80Fe20)x(Y3Fe5O12)1-x films with different components

(13)

式中：γ为旋磁比，可利用式(14)进一步计算得到g因子：

(14)

由图1(c)可看到，随着YIG组分含量的提升，线宽-频率变化关系逐渐由线性过渡到非线性。这说明随着YIG含量的增加，薄膜样品中可能产生除吉尔伯特阻尼对应的本征弛豫机制以外的其它贡献。为进一步分析该非线性关系的原因，需要分析总线宽中所包含的具体线宽成分及对应的成因。

3.2 颗粒膜部分线宽展宽机制的表达式修正

当磁场线宽-频率关系呈线性关系时，可使用式(15)进行本征线宽项的提取：

(15)

该方程是由吉尔伯特阻尼线宽项、磁非均匀性导致的与频率无关的线宽展宽项线性叠加而成；但当总线宽-频率关系变为非线性时，该方程则无法准确描述实验数据规律。就本文所制备的颗粒膜样品来说，这一非线性特征可能是由于存在双磁子散射线宽展宽以及非均匀性线宽展宽。双磁子散射线宽是由于颗粒膜内部产生的缺陷所致；从微观的角度讲，双磁子散射的强度与缺陷的尺寸、缺陷总量占比等因素相关。当外加磁场方向在转向薄膜平面外的过程中，代表双磁子散射强度的Γ(H,θH)是一个与外磁场角度相关的函数，会随着外磁场面外角度变化而发生改变。因此，更一般的双磁子散射线宽表达式为[16]：

(16)

其中:

(17)

式中：Ξ为磁拖曳函数；Hu为单轴面外各向异性场；p为缺陷在样品表面的占比；D=2A/Ms为铁磁材料的交换刚度常数。该理论模型默认缺陷为矩形，a、c即为矩形缺陷的长和宽，b为矩形缺陷的高。

3.3 颗粒膜面外转角铁磁共振的表征结果

选取6个具有代表性的外加磁场的角度值，(Ni80-Fe20)x(Y3Fe5O12)1-x薄膜面外转角度铁磁共振测试结果如图2所示。由测试结果可知，在外磁场接近于垂直薄膜表面时(图2中90°曲线所示)，主共振峰右侧出现额外旁峰。产生该旁峰的可能原因有两种，第一种是由于随着YIG掺杂含量的变化，(Ni80Fe20)x-(Y3Fe5O12)1-x薄膜趋近准均匀薄膜的过程中NiFe颗粒之间距离减小，形成大量的团簇，原本独立NiFe颗粒构成的薄膜，其内部颗粒尺寸的不均匀分布会导致共振线宽的加宽；这一现象可以理解为主共振峰是由许多共振场不同但相互接近的小共振峰叠加而成，当形成NiFe团簇后，这些小共振峰会合并形成某几个位置的共振峰。随着外磁场逐渐转向面外的过程，一些无关的线宽展宽项会被滤除，共振峰线宽减小，此时这些小的共振峰就得以显现；另一种可能是由于表面共振模式的激发，在准均匀薄膜中表面各向异性的存在会激发该共振模式，表面共振模式可能存在于外磁场垂直施加于膜面的情况[22]。

不同YIG组分含量薄膜的共振场随面外转角的变化规律如图3所示，图(a)-(f)分别对应1-6颗YIG掺杂的颗粒膜样品测试结果，可以看到随着YIG含量的增大，共振场能够达到的最大值在逐渐下降。利用上述数值计算的方法对图3中的原始数据进行拟合，通过计算所得对应的共振场与外加磁场角度之间的变化关系曲线与测试数据点集进行比较，当二者相差最小时，此时的有效磁化强度Meff及旋磁比γ的值即为实际大小；在获取有效磁化强度及旋磁比参数值后，利用这两组参数进一步对总线宽-面外磁场角度关系数据进行拟合，在此过程中，考虑三种线宽成分，分别为本征线宽(Glibert阻尼线宽项)展宽、双磁子散射线宽展宽、Mosaicity线宽展宽。

图3 变组分薄膜样品共振场面外转角度拟合(a)x≈0.848;(b)x≈0.776;(c)x≈0.64;(d)x≈0.468;(e)x≈0.371Fig 3 Outward rotation angle fitting of resonance surface of variable component film sample

3.4 颗粒膜总线宽的分离

总线宽的拟合方程如下：

ΔH=ΔHGilbert+ΔHTMS+ΔHMosaicity

(18)

利用上式对面外转角铁磁共振测试结果进行拟合，可以得到不同的线宽成分。拟合结果如图4所示，从(a)-(e)分别代表YIG 贴片为1-5颗的颗粒膜样品的总线宽随面外转角的变化。从图中可以较明显的看出，图4(a)-(c)对应的样品(NiFe含量为84.8%、77.6%、64%的颗粒膜)，其线宽主要由本征Glibert阻尼线宽和双磁子散射线宽组成，相比之下由于样品长程缺陷导致的镶嵌效应(Mosaicity)线宽展宽几乎为0。这可理解为在薄膜中仅掺杂少量YIG时，样品本身引入少量的短程缺陷，从而除本征线宽外，仍有少量双磁子散射线宽展宽项存在；而当NiFe组分为46.8%以及37.1%时，可见双磁子散射线宽展宽项在逐渐增强，同时Mosaicity效应线宽展宽项也明显增大。

图4 不同组分下的线宽分离组图(a)x≈0.848；(b)x≈0.776；(c)x≈0.64；(d)x≈0.468；(e)x≈0.371Fig 4 Line width separation group diagram under different components

从表1中可以看出，YIG 掺杂会强烈影响薄膜的阻尼因子及双磁子散射强度。除此之外，非均匀线宽展宽对样品总线宽的影响也会随着YIG含量的增加而增强，但总体来看其影响不占主导。非均匀展宽可能源于制备条件的随机涨落，此外YIG掺杂也可能会导致样品内部的非均匀，进一步使得样品各部分的磁性参数存在一个随机分布，不严格呈一个固定值。

表1 面外转角测试数据拟合结果Table 1 Fitting results of out of plane corner test data

4 结 论

通过对不同YIG组分含量的(Ni80Fe20)x(Y3Fe5O12)1-x薄膜进行研究，发现在x=0.468以下时，50 nm厚薄膜的自旋波共振模式基本消失，这是由于绝缘YIG的掺杂使得薄膜内部的涡流效应减弱所致。在Phase-FMR面外转角度测试中，当外磁场方向接近90°垂直于薄膜平面时，主共振峰右侧出现旁峰，推测为表面共振模式。同时可以发现，双磁子散射强度随着YIG含量的提升而增大，在x=0.468时，双磁子散射强度达8 771.92 A/m。可见短程缺陷在YIG含量增大后对薄膜线宽影响增大。