基于Labview 的CRC 发生器及其在卫星通信中的应用
张宏群,陈 檑,桑 峰,班勇苗,付春鑫
(1.南京信息工程大学电子信息工程学院,江苏南京 211800;2.上海卫星工程研究所,上海 201109)
在卫星测控通信系统中,常采用指令-应答式的通信模式[1]。地面应用系统发送指令,星载设备接收指令并执行相应的操作,同时将执行的情况下发给地面应用系统。为了确保指令的正确性,可采用差错控制编码来提高数字消息传输的准确性,但会使通信系统的有效性大打折扣,消耗了较多的信道资源[2]。循环冗余校验(Cyclic Redundancy Check,CRC)编码是一种常用于通信的错误检测码。CRC 编码不能纠错,但是可以有效地检测错误,从检错能力来看,它不能发现的错误的发生几率仅为0.004 7%以下[3]。同时采用CRC 编码所需代价较小,以CRC-16为例,可编码的信息码元长度达到37 251 bit[4],而监督码元只有16 bit,编码效率为99.96%,极大地减少了编码带来的链路有效性。由于空间辐射效应对电子器件的影响及无线链路的复杂性,卫星通信经常存在误码。针对这些错误,对信息码元进行CRC 编码,配合检错重发(ARQ)可以有效降低其影响,提高了通信可靠性。
1 CRC编码介绍
CRC 码是线性分组码中的一种循环码,其本质是一种缩短的循环码。在系统线性分组码(n,k)中,前k位为信息码元,后r位(r=n-k) 为监督码元。监督码元和信息码元是通过线性方程联系起来的。线性分组码具有封闭性,即任意两个许用码组之和(模2 和)仍为一个许用码组[5]。例如,通常的偶校验码即为线性分组码,设k=2,则监督码元a0与信息码元a1、a2之间的关系为a0=a2⊕a1。因此,许用码组集为{(0,0,0),(0,1,1),(1,0,1),(1,1,0)},可以看出,其具有封闭性。
循环码是线性码的一个子类。在满足线性码特性的同时,其还满足任一许用码组经过循环移位后的码组仍为一个许用码组。即若(an-1,an-2,…,a0)为一个循环码组,其任意循环移位构成的码组也为循环码组。
可以用多项式来描述循环码,设一个n元二进制循环码元序列为A=(an-1,an-2,…,a0),(ak∈{0,1},k=0,1,…,n-1),将其用码多项式来表示,则可以表示为:

循环码的特点如下:

根据循环码的特点可知,所有的A(i)(x) 也为循环码。
根据代数理论[6],A(i)(x)也可以用下式来确定:
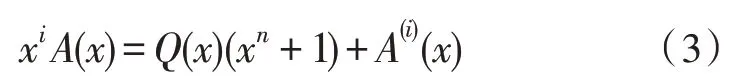
其中,Q(x) 为xiA(x) 除以(xn+1) 的商式,A(i)(x)为余式。
循环码可以完全由其码组长度n及其生成多项式g(x)来确定,生成多项式g(x)是一个能除尽xn+1的多项式。
信息码组M(x) 与生成多项式g(x) 及许用码组A(x)之间的关系可以表示为:

A(x)对应码组的前k位对应的多项式即为M(x),后n-k位是监督码元,因此,A(x)也可以表示为:
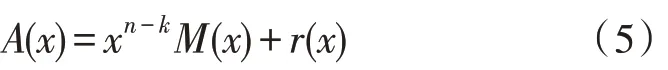
根据式(4)和式(5)可得:

因此,监督码元r(x)的求法可以简化为xn-kM(x)除以g(x)并取余式。
CRC 码是循环码中的一种,其能够检测出如下的错误[7]:
1)长度小于或等于n-k的突发错误(突发错误是一个错误序列,首尾均为1,错误序列长度定义为包括首尾1 在内的错误所波及的段落长度);
2)大部分长度等于n-k+1 的突发错误(漏检概率为2-(n-k-1));
3)大部分长度大于n-k+1 的突发错误(漏检概率为2-(n-k));
4)所有奇数个随机错误;
5)所有错误个数小于或等于dmin-1 个错误(dmin为许用码组的码距)。
目前,常用的CRC码标准[8]有4种:CRC-12、CRC-16、CRC-CCITT、CRC-32,其生成多项式分别为:

2 使用Labview产生CRC校验
基于式(6)利用Labview 产生CRC 校验算法[9],以CRC-CCITT 为例,其生成多项式为g(x)=x16+x12+x5+1,根据式(6),设计求解信息码元M(x)的CRC校验码的过程如下:
1)将M(x) 向右移动r=16位,得到x16M(x)(文中设其为N(x)),即在信息码元后面添加16 个0;
2)N(x)对g(x)取余式,采用按位异或来实现除,具体做法为:
①将N(x)与g(x)高位对齐,若N(x)最高位为0,则删除最高位后替换N(x),直到N(x)高位为1;
②将N(x) 高2~17位与g′(x)=x12+x5+1 按位异或(由于此时N(x)最高位已经为1,而g(x)高位也为1,异或值必然为0,因此可使用g′(x)进行异或),异或值添加到N(x)剩余位的前面,得到N1(x),以N1(x)取代N(x);
③重复①和②的步骤,直到N(x)次数小于16。此时的N(x)即为M(x)的CRC-CCITT校验码;
④将M(x)和其生成的CRC-CCITT 校验码进行拼接,即为所需的码组。
使用Labview 设计的CRC 校验产生的图形化程序框图和流程图分别如图1、2 所示。
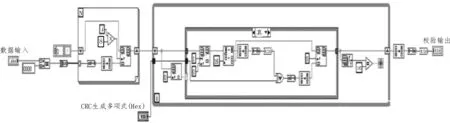
图1 使用Labview产生CRC校验的图形化程序框图

图2 使用Labview产生CRC-CCITT校验流程图
由于CRC-CCITT 的校验多项式为16 次多项式,通常需要17 bit 的变量参与运算,在计算机实际应用中,通常需要开辟32 bit 的变量存储空间,造成了存储和计算资源的浪费。文中利用CRC-16 多项式最高位为1 的特点[10],提出了将其简化为15 次多项式的方案,处理时只需要开辟16 bit 的变量存储空间即可,因此,相比与文献[11-12]中的方法,文中的算法更优。
在接收端进行CRC 译码时,其算法与图1 相似,不同的是,进行运算前不需要添加16 个0,直接将信息码元与生成码元进行异或,如果接收的信息未产生误码,其校验值应为0。
在编程时,考虑到程序的通用性,程序可以针对所有的16次CRC生成多项式进行CRC校验运算。以输入字符“1244 3104,1244 0A04”为例,CRC-CCITT(去除高位1 后的十六进制生成多项式为1021)和CRC-16(去除高位1 后的十六进制生成多项式为8005)的运算结果分别为4182 和514E,如图3、4所示。
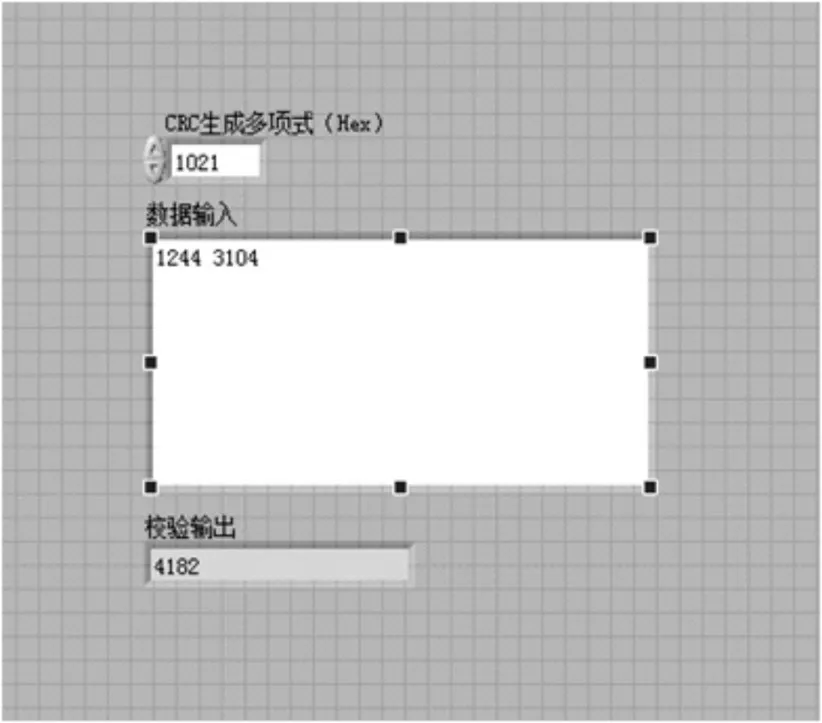
图3 CRC-CCITT计算实例
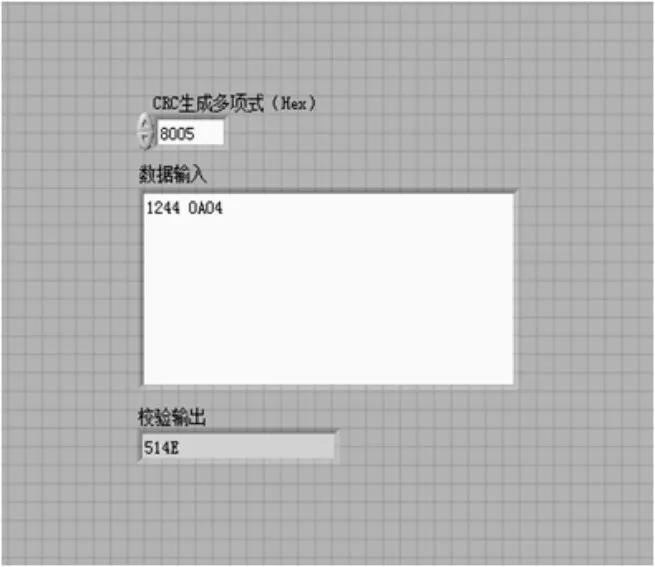
图4 CRC-16计算实例
3 基于CRC的可靠性指令设计
在卫星通信系统中,可靠性指令设计通常要求满足以下条件:
1)对于不包含数据的指令,要求指令标识符出现误码时星上不能出现错误操作;
2)对于指令出现误码的情况,星上要能正确地进行识别,并请求地面重发;
3)对于包含数据的指令,要求正确地识别指令,在识别指令后,数据无论是否产生误码,应全部接收;
4)指令之间应有一定的区分能力,对于地面连续发出的多条指令应加以区分;
5)指令格式应仅可能简单,以提高信道的利用率。
为了满足上述条件,设计了一种指令格式方案,该指令格式适用于上行链路和下行链路。由同步头、指令计数、指令标识、数据长度、CRC 校验和数据构成,可以满足使用条件。
同步头为数据开始的标志。为了防止指令格式中的同步头出现误码而不能接收的情况,同步头的长度可以适当进行选取,并进行容错处理。上行链路和下行链路均采用不同的同步头,且码距应尽可能长。
指令计数可以采用从00~FF 循环计数,地面每发一个指令,指令计数加1,至FF 后回归到00。这样每256 条指令才会出现一个重复的指令计数。指令之间具备了一定的区分能力。星上返回的内容中也含有相同指令计数信息,这样地面就可以判断指令之间的对应关系。
指令标识是区分指令的标识,选择码距较长的码字,数据长度是指令数据的长度。数据部分代表指令数据,其长度与“数据长度”部分一致[13]。
指令计数、指令标识和数据长度采用CRC 校验,根据不同的应用情况可以选择CRC-16、CRC-32 或者CRC-CCITT。地面系统CRC 编码的产生方法可以采用文中第2 节的方法,星载系统的CRC 编码产生方法可以用硬件来实现[14]。
在这种指令格式中,由于使用了CRC 校验,若指令计数、指令标识和数据长度任何一部分产生误码,CRC 校验值会以几乎百分百的概率检验出错误。若信号开始传输时接收到同步头,但CRC 校验该数据出现错误,则星上应在向地面的响应内容中进行反馈,反馈内容包括指令计数等信息,便于地面应用系统根据实际情况进行处理。对于包含数据的指令,只要CRC 校验码正确,表明数据长度正确,程序即按照数据长度进行数据接收,根据实际应用情况,数据的误码控制可以由其他的编码方式来实现[15-20]。
4 结论
文中根据CRC 理论设计了一种实用的软件产生CRC 编码的方法,并使用编程语言Labview 来实现,这种实现方式能够快速进行CRC 编码运算,不用理会复杂的语法结构、众多的数据类型及反复编译、查找错误。同时根据针对卫星通信系统应用中要求指令高可靠的需求,将CRC 理论应用到星地指令设计中,提出了一种较为新颖、可靠、有效的指令方案,并对其进行分析,相关实践表明,该算法可实现性强、资源开销小,适合应用于存储空间和处理速度受限的场合。

