含参数集值向量优化问题超有效点集的连通性

吴昌耀， 陈剑尘， 何焕民

1. 南昌航空大学， 数学与信息科学学院， 南昌 330063； 2. 汕头市林百欣科学技术中等专业学校， 广东 汕头 515057

关于集值向量最优化问题， 自文献[1-2]， 在赋范向量空间中， 给出超有效点的相关定义以来， 已有不少专家和学者对超有效性进行研究[3-6]． 受文献[6]启发， 本文对含参数的集值向量优化问题超有效点集的连通性进行研究． 首先， 引入含参数超有效点集的相关概念， 然后， 在含参数的目标集值映射是C-弧连通的， 可行域为弧连通紧且参数扰动的情况下， 证明了含参数集值向量优化问题的超有效点集的连通性．

1 预备知识

本文假设X，Y和Z均为Hausdorff局部凸的拓扑线性空间，Y*为Y的拓扑对偶空间．N(0)为Y的零点邻域基． 设M⊂Y且M≠∅， 分别用int(M)， cl(M)， conv(M)， 表示M的内部、 闭包以及凸包． 由M生成的锥记为cone(M)={lm：l≥0，m∈M}．

设C⊂Y为非空闭凸点锥， 且int(C)≠∅(其中int(C)表示C的内部)．C*为C的拓扑对偶锥， 记为

C*={f∈Y*：f(c)≥0， ∀c∈C}

C#为C的对偶锥C*的拟内部， 记为

C#={f∈Y*：f(c)>0， ∀c∈C{0}}

非空凸子集B⊆C称为C的基， 若C=cone(B)且0∉cl(B)． 显然有：

另外， 以下结论也是成立的：

定义1[7]设D⊂Y为非空子集．y*∈D称为D关于C的有效点， 记为y*∈E(D，C)， 如果(D-y*)∩(-C)⊂C． 如果C为点锥， 则y*∈D为有效点⟺(y*-D)∩C={0}⟺(y*-C)∩D={y*}．

定义2[7]设D⊂Y为非空子集．y*∈D称为D关于C的超有效点， 记为y*∈SE(D，C)， 设N(0)是Y的零点邻域基， 若对∀V∈N(0)， 都∃U∈N(0)， 使得

cl(cone(D-y*))∩(U-C)⊂V

注1显然， 超有效点必为有效点， 即SE(D，C)⊂E(D，C)． 反之不成立．

引理1[3]设D⊂Y为非空子集，C⊂Y是闭凸点锥， 且C有有界基B， 则

SE(D，C)=SE(D+C，C)

接下来， 我们介绍一下集值映射的一些基本概念和结论．

tF(x1)+(1-t)F(x2)⊂F(tx1+(1-t)x2)+C

conv(F(A))⊂F(A)+C

φx1， x2(0)=x1，φx1， x2(1)=x2

(1-t)F(x1)+tF(x2)⊆F(φx1， x2(t))+C

(1-t)F(x1)+tF(x2)⊆F(φx1， x2(t))-C

注3C-弧连通的必为C-类凸的， 反之不成立．

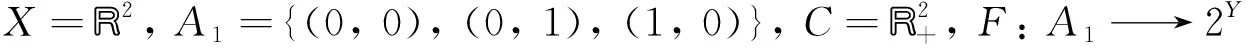
F(x)={(x1，x2)， (1， 1)}， ∀x=(x1，x2)∈A1

则F在A1上是C-类凸的， 但F不是C-弧连通的．

SE(F(A)，C)=SE(F(A)+C，C)=SE(conv(F(A))，C)

h(y*)=min{h(y)|∀y∈F(A)}

SE(F(A)，C)=∪{PE(F(A)，h)|h∈int(C*)}

其中

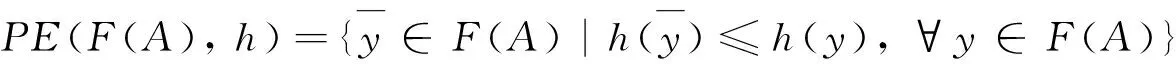
PE(F(A)，h)=PE(conv(F(A))，h)

称F在A上是上半连续的， 如果F在A上每一点均是上半连续的．

定义7[15]设X为拓扑线性空间． 集合A⊂X称为有界， 如果它能被X中的每一个零元邻域吸收， 即对于每一个V∈N(0)， 存在一个l>0， 使得A⊂lV．

定义8[15]设X为拓扑线性空间， 则在X上由X*生成的F-拓扑称为弱拓扑， 记为TX*或TW． 相应的局部凸空间记为(X，TX*)， (X，TW)或XW．

若集合A关于弱拓扑有界， 则称A为弱有界， 或称为A⊂XW有界．

引理8[15](Banach-Mackey)设X为局部凸空间， 则A⊂X有界当且仅当A⊂XW有界．

引理9[16]设X1，X2，…，Xn是n≥1个弧连通空间． 则积空间X1×X2×…×Xn也是弧连通空间．

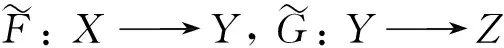
2 含参超有效点集的连通性

考虑以下含参数集值向量优化问题(PSVOP)：

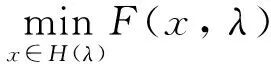
定义9设x*∈H(λ)，y*∈F(x*，λ)称为F(H(λ)，λ)关于C的(PSVOP)中的含参超有效点， 设N(0)是Y的零点邻域基， 若对∀V∈N(0)， 都∃U∈N(0)， 使得

cl(cone(F(H(λ)，λ)-x*))∩(U-C)⊂V

(PSVOP)中的含参超有效点的全体记为SE(F(H(λ)，λ)，C)．

命题1设X，Y，Z均为Hausdorff局部凸的拓扑线性空间，E⊂X为非空的紧子集， 且E为弧连通的，Λ⊂Z为非空的弧连通集，C⊂Y为闭凸点锥， 且C具有有界基B． 如果同时满足下列条件：

则SE(F(H(λ)，λ)，C)， ∀λ∈Λ是非空的连通集．

证若以下无特别说明， 都假设任意取定λ∈Λ，F(x，λ)均定义在H(λ)上．

由于E为弧连通的，Λ为弧连通的， 则由引理9可知，E×Λ也是弧连通的．

又因为含参数的目标集值映射F在E×Λ是C-弧连通的， 且H(λ)×{λ}是弧连通的， 故F在H(λ)×{λ}是C-弧连通的． 即F(x，λ)在H(λ)上是C-弧连通的． 由引理2可知

F(H(λ)，λ)+C

是凸集． 由注2知，F(x，λ)是H(λ)上的C-类凸的映射． 又因为C⊂Y是具有有界基B的凸锥， 所以由推论1知

SE(F(H(λ)，λ)，C)=∪h∈int(C*)PE(F(H(λ)，λ)，h)

SE(F(H(λ)，λ)，C)≠∅， ∀λ∈Λ

又由引理3知， ∀λ∈Λ，

SE(F(H(λ)，λ)，C)=SE(F(H(λ)，λ)+C，C)=SE(conv(F(H(λ)，λ))，C)≠∅

下面证明SE(F(H(λ)，λ)，C)为连通集， 证明过程分为3部分．

首先定义集值映射

并令

φ(h)=PE(conv(F(H(λ)，λ))，h)

对∀h∈int(C*)， 设

PE(conv(F(H(λ)，λ))，h)={y*∈(conv(F(H(λ)，λ)))|h(y*)≤h(y)， ∀y∈F(H(λ)，λ)}

因为PE(F(H(λ)，λ)，h)≠∅， 由引理5可知

PE(conv(F(H(λ)，λ))，h)=PE(F(H(λ)，λ)，h)≠∅

任取y1，y2∈PE(conv(F(H(λ)，λ))，h)，t∈(0， 1)， 则有

y1，y2∈conv(F(H(λ)，λ))

设y=ty1+(1-t)y2， 因为conv(F(H(λ)，λ))是凸集， 所以y∈conv(F(H(λ)，λ))， 且对∀z∈conv(F(H(λ)，λ))， 有

h(y)=h(ty1+(1-t)y2)=th(y1)+(1-t)h(y2)≤th(z)+(1-t)h(z)=h(z)

即y=ty1+(1-t)y2∈PE(conv(F(H(λ)，λ))，h)． 因此PE(conv(F(H(λ)，λ))，h)为凸集， 从而PE(conv(F(H(λ)，λ))，h)为连通集．

故φ(h)=PE(conv(F(H(λ)，λ))，h)也为连通集．

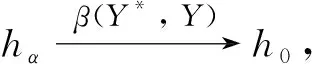
φ(hα)⊄V∀α∈Δ

由于F(H(λ)，λ)是弱紧集， 不失一般性， 故可以假设网{yα：α∈Δ}， 使得

且yα∈φ(hα)， 但是

yα∉V∀α∈Δ

(1)

又由于V是开集， 因此y0∉V．

由推论1和引理3可得，

yα∈φ(hα)=PE(conv(F(H(λ)，λ))，hα)⊂SE(conv(F(H(λ)，λ))，C)=SE(F(H(λ)，λ)，C)

因为yα∈φ(hα)， 则有

hα(yα)≤hα(z) ∀z∈conv(F(H(λ)，λ))

(2)

设K： =F(H(λ)，λ)， 由于K是弱紧的， 因此，K是弱有界的． 再由引理8可知，K是Y中的有界集．

定义

PK(h*)=sup{|h*(y)|：y∈K}，h*∈Y*

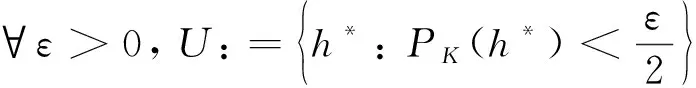
从而对∀α≥α0， 有

因此， 对∀y∈K， 有

且有

(3)

(4)

由(3)式和(4)式得

于是

对(2)式两边同时取极限， 得

h0(y0)≤h0(z) ∀z∈conv(F(H(λ)，λ))

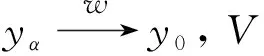
yα∈V∀α≥α2

这与(1)式矛盾， 故所定义的集值映射φ在int(C*)上是上半连续的．

综上， 由引理7知， ∪{φ(h)：h∈int(C*)}是连通的． 即∪h∈int(C*)PE(conv(F(H(λ)，λ))，h)是连通的． 又由推论1和引理5可得

SE(F(H(λ)，λ)，C)=∪h∈int(C*)PE(F(H(λ)，λ)，h)=∪h∈int(C*)PE(conv(F(H(λ)，λ))，h)

故SE(F(H(λ)，λ)，C)是非空的连通集．

定理1设X，Y和Z均为Hausdorff局部凸的拓扑线性空间，E⊂X和Λ⊂Z均为非空的弧连通紧子集，C⊂Y为闭凸点锥，C具有有界基B． 如果同时满足下列条件：

则∪λ∈ΛSE(F(H(λ)，λ)，C)是非空的连通集．

证定义集值映射

使得T(λ)=SE(F(H(λ)，λ)，C)． 由命题1可知， 对于∀λ∈Λ，T(λ)=SE(F(H(λ)，λ)，C)≠∅， 因此， ∪λ∈ΛSE(F(H(λ)，λ)，C)≠∅．

下面将证明过程分为3步进行：

由命题1知， 对于∀λ∈Λ，SE(F(H(λ)，λ)，C)是连通的， 因此

T(λ)=SE(F(H(λ)，λ)，C)

是连通的．

T(λi)⊄V∀i∈I

即∃{yi：i∈I}， 使得

yi∈T(λi)，yi∉V∀i∈I

(5)

其中I为指标集． 由推论1和引理5知

SE(F(H(λ)，λ)，C)=∪h∈int(C*)PE(F(H(λ)，λ)，h)

又由于

SE(F(H(λ)，λ)，C)=∪h∈CΩPE(F(H(λ)，λ)，h)

故有

T(λi)=∪h∈CΩPE(F(H(λi)，λi)，h)

由于yi∈T(λi)， 则∃hi∈CΩ， 使得

yi∈PE(F(H(λi)，λi)，hi)

因为网{hi}⊂CΩ， 且由CΩ是紧的， 不妨设h0∈CΩ， 使得

从而有

hi(yi)≤hi(vi)， ∀vi∈F(H(λi)，λi)

(6)

由于H(λ)及F(x，λ)均是下半连续的， 故由引理10知，F(H(λ)，λ)关于λ是下半连续的， 从而， 对于∀v0∈F(H(λ0)，λ0)， ∃vi∈F(H(λi)，λi)， 使得

记L： =∪λ∈ΛF(H(λ)，λ)． 因为G是上半连续的， 且G(λ)=F(H(λ)，λ)是弱紧的， 故L是弱紧的． 因此，L是弱有界的． 又由引理8可知，L是有界的．

这里定义

PL(h)=sup{|h(y)|：y∈L}，h∈Y*

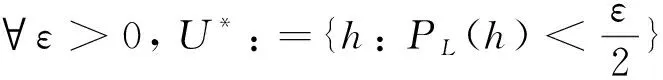
即有

(7)

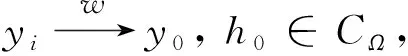
(8)

由(7)式和(8)式得

∀i≥i0， ∀i≥i1

因此

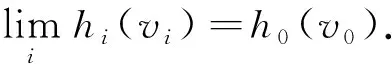
对(6)式两边同时取极限得

h0(y0)≤h0(v0) ∀v0∈F(H(λ0)，λ0)

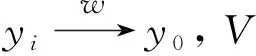
yi∈V∀i≥i2

这与(5)式矛盾． 故T在Λ上是上半连续的．

综上所述， 由引理7知， ∪λ∈ΛSE(F(H(λ)，λ)，C)是连通的． 证毕．