一种应用于人体活动识别的迁移学习算法

赵 海, 陈佳伟, 施 瀚, 王 相

(东北大学 计算机科学与工程学院, 辽宁 沈阳 110169)

人体活动识别是通过各种传感器采集人体行为数据,并利用计算机技术对其进行分析来理解人体各种行为活动的过程,它在老人监护[1]、健康监测[2]、娱乐和运动等多个方面都有着良好的应用前景.随着智能手机、智能手表等电子设备的普及,利用这些随身携带的电子设备来识别人体活动成为研究热点.范长军等[3]利用智能手机和手环组成一个体域网并基于此设计了一套在线人体识别系统,殷晓玲等[4]提出了一种利用智能手机内置的传感器来识别人体运动状态的方案,Fu等[5]则设计了一种无线传感器节点来解决用户活动个性化识别的问题.

机器学习训练过程的前提是数据独立同分布,然而每个人的数据分布是不一致的,个体之间行为活动的差异导致传统模型的识别精度不高[6].迁移学习常被用来解决在不同任务域中进行知识迁移的问题,它可以良好地解决由于数据分布不一致而导致传统机器学习失效的问题.迁移学习已经被证明在很多方向都有着良好表现,如Hou等[7]利用迁移学习实现了跨领域的语音识别,彭雨荷等[8]提出了一种基于迁移学习的异常流量检测方法.研究人员开始将人体活动识别和迁移学习相结合来解决识别精度不高的问题.Elnaz等[9]利用生成对抗网络在人体活动识别领域进行迁移学习,在超过66%的实验中优于其他方法.Niu等[10]构建了一个在智能家居场景下优于基准方法的多源迁移学习的人体活动识别模型.

如何降低不同任务域之间的分布差异是迁移学习要解决的关键问题[11].最近的研究工作已经探索出两种不同的思路:1)特征匹配,它主要通过特征变化的方式,将两个不同分布的数据集映射到同一个高维空间,在这个高维空间中,它们之间的数据分布差异被缩小[12];2)实例加权,这种方式的主要思想是通过不断地对一个任务域中的实例数据进行加权,直到它们之间的数据分布差异被缩小[13-14].

大多数的迁移学习算法都是基于上面的两种思路,然而无论是基于特征匹配的迁移学习算法还是基于实例加权的迁移学习算法,都忽视了噪声样本对数据分布的影响.噪声样本是指在数据采集的过程中产生较大偏差或被错误分类而导致迁移效果下降的样本.在人体活动识别领域常利用可穿戴传感器采集人的运动信号,在采集过程中必然会产生噪声样本,而不论是基于哪种思路,都没有考虑将噪声样本从数据集中剔除.存在噪声样本,不但会影响最终的迁移效果,还会影响对活动识别的准确性.

本文在传统算法的基础上,增加了对噪声样本的筛选过程,引入马氏距离作为衡量噪声样本的标准,提出了一种应用于人体活动识别的迁移学习算法T-WMD.并将该算法应用于两个真实世界人体活动识别数据集上,结果表明本文提出的算法可以有效地提高人体活动识别的准确率,优于其他对比算法.

1 问题定义和相关工作

1.1 问题定义

本文基于可迁移环境的人体识别场景进行详细的问题定义,考虑到噪声样本对迁移效果的影响,本文要解决的问题是如何利用已知的标签信息来对源域中的样本进行筛选,从而剔除噪声样本,并提高迁移效果,文中常用符号如表1所示.

表1 符号及说明Table 1 Notations and descriptions

本文的目标是:1)基于特征匹配的方法减小源域和目标域之间的分布差异；2)通过样本选择的方式筛选并剔除噪声样本,提高迁移性能.

1.2 基于特征匹配的迁移学习算法

特征匹配方法是通过特征变换的方式互相迁移,来减少源域和目标域之间的差异,或者将源域和目标域的数据特征变换到统一的特征空间中,然后利用传统的机器学习方法进行分类识别.本文引入迁移成分分析[14](transfer component analysis,TCA),是基于特征匹配思想的经典迁移算法.TCA假设存在一个特征映射ø,使得映射后数据分布P(ø(xs))≈P(ø(xt)).值得一提的是,TCA假设如果边缘分布接近,那么两个领域的条件分布也会接近,即条件分布P(ys|ø(xs))≈P(ys|ø(xt)).

具体而言,TCA利用最大均值差异(maximum mean discrepancy, MMD)来计算源域和目标域映射后的距离:

(1)

其中,n1和n2分别为源域和目标域的样本个数.

将式(1)展开,引入核矩阵

(2)

其中,K=[ø(xi)Tø(xj)].

以及MMD矩阵L,它的每个元素的计算方式为

(3)

将矩阵K进行分解:

(4)

(5)

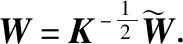
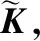
MMD(xs,xt)=tr((KWWTK)L)=tr(WTKLKW) .

(6)

为了减小源域和目标域之间的分布差异,即MMD距离,TCA将优化目标定义为

(7)

s.t.WTKHKW=Im.

最后,解决式(7)的拉格朗日对偶问题:

(8)

得到的矩阵W就是映射并降维后的样本,它的解为(KLK+μI)-1KHK的前m个特征向量,其中m≤n1+n2-1.

1.3 距离度量方法

距离是用来衡量两个数据域之间差异的基础手段,常用的距离度量方法有很多,例如欧氏距离、最大均值差异和马氏距离[15]等.本文所提出的算法使用的是马氏距离,由印度统计学家Mahalanobis提出,是基于样本分布的距离.它是一种有效计算两个未知样本集的相似度的方法,与欧氏距离相比,它考虑到各种特性之间的联系并且与尺度无关.在计算样本大、特征多的人体运动数据时,简单的计算方式可以大幅度减少计算时间,提高算法运行效率.

(9)

其中:μ为样本分布的均值;S是样本分布的斜方差矩阵.

2 T-WMD算法介绍

本文提出基于加权马氏距离的迁移学习算法T-WMD.传统的算法在进行迁移学习时,只考虑缩小源域和目标域之间的距离,没有考虑噪声样本对迁移效果的影响,T-WMD算法在传统算法的基础上加入了筛选噪声样本的步骤.

T-WMD算法首先利用TCA将源域数据集和目标域数据集进行特征映射和降维,从而达到缩小源域和目标域之间数据边缘分布差异的目的,然后利用本文提出的基于马氏距离的样本筛选算法WMD对源域样本进行噪声样本的筛选,这样做的好处有:1)可以缩小源域和目标域之间的条件分布差异;2)将噪声样本筛选出来,从而提升迁移效果和识别准确率.算法具体流程如图1所示.

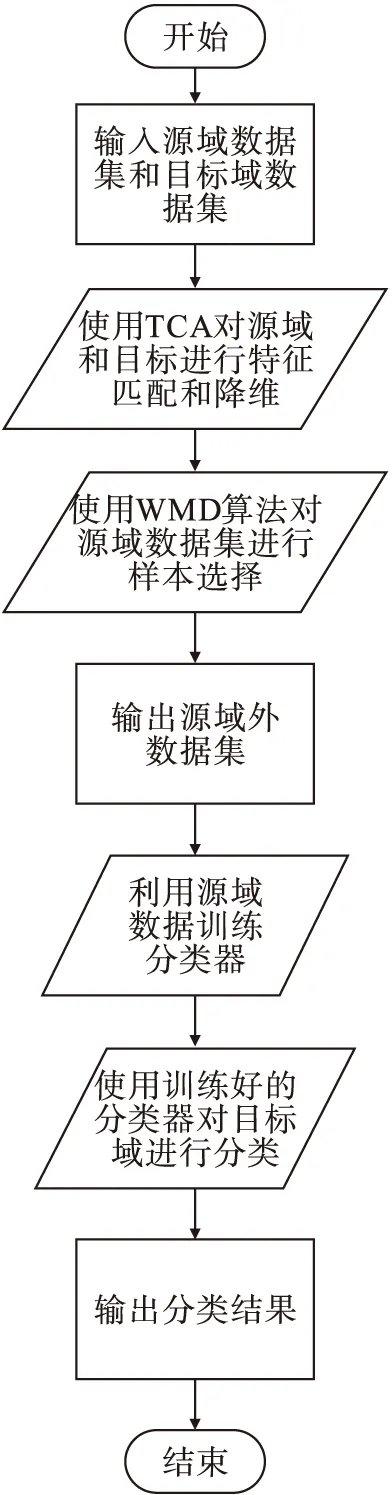
图1 T-WMD算法流程图Fig.1 Flow diagram of T-WMD

2.1 基于马氏距离的样本选择算法WMD

噪声样本是影响迁移学习效果和识别准确率的原因之一,本文所提出的WMD算法通过计算源域数据Ds和带标签的目标域DL之间的马氏距离来对源域中的样本进行筛选.

首先,计算DL各类样本的均值μc:

(10)

其中:μc是DL中第c类样本的均值;nc是第c类样本的总数;xLi是DL中第c类的第i个样本.

其次,计算DL中各类样本的协方差矩阵Sc:

(11)

其中,xLm是DL中样本的第m个特征.

然后,计算Ds中的样本到DL中各类的马氏距离:

(12)

其中:xi表示源域Ds中的第i个样本;yi表示样本xi的标签;α是本文引入的权重因子.

最后,当xi对DL中各类马氏距离计算完成后,判断和xi距离最近的类的标签与yi是否相同,如果相同则保留这个样本,否则删除.

本算法在马氏距离算法的基础上,根据生理信号采集过程中易产生噪声样本的特点引入了权重因子α.

由于人行为的不确定性,在使用可穿戴传感器针对各种不同动作进行生理信号采集的过程中,可能会采集到不属于同一类的噪声信号,也有可能导致本属于同一动作的部分信号相较于其他信号产生较大的差异,这两部分信号都有可能对最后的迁移效果和识别分类的准确率造成影响.

为了剔除出不属于同一类的噪声信号,同时筛选出产生较大偏差的信号,本算法引入权重因子α.在计算Ds中的样本对DL中各类样本的马氏距离时,如果两者属于同一类,则利用式(13)进行计算:

(13)

其中,α∈(-1,1].当α→-1时,会使样本xi对同类的计算的马氏距离减少,从而保留下产生较大偏差的同类样本.当α→1,会使样本xi对同类的计算的马氏距离增加,从而保留下与目标域距离最近的同类样本.算法流程见算法1.

算法1 WMD

输入:

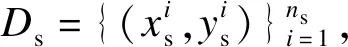
过程:

1.计算DL中各类的均值μc;

2.计算DL中各类的协方差矩阵Sc;

3.forDs中的每个样本xido:

forDL中每个标签cdo:

根据式(12)计算Ds中的样本xi到DL中c类的马氏距离;

判断距离xi最近的类标签与yi是否相同,相同则保留xi,不同则删除xi.

4. end

5.end

输出:

样本选择后的源域数据集Ds.

2.2 T-WMD算法

T-WMD算法的基本流程是:首先利用TCA算法将源域数据集和目标域数据集同时使用核函数映射到高维希尔伯特空间,再进行降维操作,来缩小边缘分布差异.然后使用本文提出的样本选择算法WMD对映射和降维后的源域数据进行噪声样本的筛选,来缩小条件分布差异.最后使用处理好的源域数据训练分类器,将目标域数据送入分类器中得到分类结果.算法流程见算法2.

算法2 T-WMD

输入:

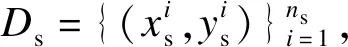
过程:

1.投影后的Ds,DL和DU= TCA(Ds,Dt,m);

2.样本选择后的Ds= WMD(Ds,DL,α);

3.把样本选择后的Ds作为训练集输入到分类器f中进行训练;

4.使用分类器f对投影后的DU进行分类;

输出:

无标签目标域DU的标签.

本文提出的算法主要由4个步骤组成:第一步投影和降维的时间复杂度为O(N),第二步样本选择的时间复杂度为O(MN),第三步训练分类器和第四步使用分类器进行分类的时间复杂度均为O(N).所以T-WMD算法的时间复杂度为O(3N+MN)≈O(MN),其中M为标签个数,N为样本个数.

3 实验结果与分析

3.1 实验数据集

为了验证T-WMD算法的有效性,本文使用了两个真实世界的人体活动识别数据集来进行实验.它们是PAMAP2数据集[16]和mHealth数据集[17-18],分别来自德国人工智能研究中心和格拉纳达大学.

PAMAP2数据集包含18种不同体育活动的数据(步行、骑自行车、踢足球等).数据集选取9位受试者,令他们佩戴3个惯性测量单元和心率检测器.在进行信号采集过程中,要求受试者遵循12种不同活动的协议.数据文件包含54行,每行有一个时间戳、一个活动标签和52个原始感官数据属性.

mHealth数据集包含了12种不同的体育活动数据.数据集采集了10名不同身材的志愿者在体育锻炼时的身体运动和生命体征记录.mHealth将传感器放置在实验对象的胸部、右手腕和左脚踝,来测量身体各个部位在运动时的加速度、转弯速率和磁场方向.除此之外,放置在胸部的传感器还提供2导联的心电测量.

3.2 实验流程及设置

本实验从两个数据集中选取了坐、躺、走四类生活中常见的人体活动样本,在这些样本中选取了在x、y、z三个方向上的胸部、手臂和脚踝的加速度以及手臂、脚踝的角速度和磁场强度共计21维数据.将这些数据进行标准化处理,并对每一维数据进行了特征提取工作,提取的特征包括平均值、方差、极差、偏度和峰度等时域特征、前5个最高峰值以及对应的频率和11个自相关系数共计546维特征.本实验所使用的处理后的数据集信息如表2所示.

表2 数据集说明Table 2 Description of data set

本实验选择的对比算法包括基于特征匹配的迁移算法TCA[14]、基于实例加权的迁移算法TJM[11]、基于联合分布自适应的迁移算法BDA[19]和JDA[20],为了突出算法性能的比较结果,本文选择KNN(K=1)作为基础分类器.

本文提出的算法需要设置两个超参数,维度m和权重因子α,这两个参数均为经验参数,本文将在3.4节中对经验参数进行参数敏感性分析,以便确定α最佳的取值范围.

实验的具体流程:首先对PAMPA2和mHealth数据集进行特征提取和标准化处理,然后使用KNN,TCA,TJM,BDA和T-WMD算法对构建的迁移学习任务进行实验,得到实验结果并分析.

3.3 实验结果分析

本实验以分类准确率作为评价指标,将PAMPA2和mHealth数据集分别作为源域和目标域构建了两组迁移任务,实验结果如表3所示.

表3 对比算法与本文算法的准确率Table 3 The accuracy between the proposed algorithm and the contrast algorithm %

由实验结果可以发现,本文提出的算法在两次实验中都获得了较高的准确率,分别为76.04%和67.64%.与未采用迁移学习的传统机器学习算法KNN(假设训练数据与测试数据满足独立同分布IID条件)相比,准确率高出了3.12%和4.71%;与其他迁移学习算法相比,准确率较最高的算法高出1.46%和2.49%,较最低的算法高出23.33%和4.93%.

TCA算法是基于特征匹配的迁移学习算法,假设通过拉近源域和目标域之间的边缘分布来使条件分布接近.TCA没有考虑样本的因素,这使得当该算法应用在生理信号这种具有噪声样本的数据集时,迁移效果不好.

TJM算法是对TCA的改进,进一步考虑到样本对迁移效果的影响,通过有限次的循环来给样本进行加权.但是循环的次数会根据数据集的不同而变化,要找到最优的循环次数可能要耗费大量的时间,而且仅仅加权并不能完全剔除噪声样本对迁移效果的影响.在本实验中TJM的迁移效果不好,其原因是TJM算法是对所有样本进行加权,但并没有考虑有噪声样本的数据集的情况,在有噪声样本的数据集中,这种做法可能加大了噪声样本的影响,导致迁移效果下降.

JDA算法是从分布自适应的角度提出的迁移学习算法,BDA算法是对JDA算法的提升.两者均没有完全剔除噪声样本对迁移学习效果的影响.对于生理信号这类容易产生噪声的数据集来说,迁移效果不好.

相较于其他对比算法,本文提出的算法考虑了特征和样本两个维度,利用部分有标签的目标域,对源域中的样本进行筛选,剔除噪声样本,提升了迁移效果.

3.4 参数敏感性分析

在本文提出的算法中,需要提前设置权重因子α.权重因子α的值会对剔除噪声样本的数量产生影响.本文按照TCA和JDA等算法原文中的设置,统一设置m为30,在两组迁移任务上,使用遍历的方式在[-1,1]范围内查找α的最优取值范围.图2展示了在维度m为30时,两次实验中权重因子对分类准确率的影响.

图2 权重因子对准确率的影响Fig.2 The influence of weighting factor on accuracy

由图2可以发现,不同的权重因子会影响分类准确率,在这两组迁移任务上,当α→-1时,被删除的噪声样本数量减少,噪声样本的存在影响着迁移效果,导致准确率下降;而当α→ 1时,被删除的噪声样本数量增多,当α过大时还会影响正常的样本,导致准确率下降.因此,从图2中可以得到,α的最优取值范围应该在[-0.75, 0.5],在这个区间中选取α可以达到最高的准确率,且不同的α对准确率的影响不是很大.

4 结 语

本文针对生理信号中噪声样本会影响迁移效果的问题,通过利用部分有标签的目标域来对源域样本进行筛选,剔除噪声样本,提出了T-WMD算法,该算法同时考虑特征和样本两个维度.并在两个公开的活动识别数据集上进行了实验,同时与其他5种算法进行对比.实验结果表明,本文提出的方法可以有效地提高活动识别的准确率,提升迁移效果,优于其他对比算法.

本文提出的算法还有不足之处.在T-WMD算法中,需要指定权重因子的值,但目前只能使用遍历的方式找到权重因子最优的取值范围,如何确定最佳的α值,找出与α有关的因素,这是未来要解决的问题.