基于FDA-MIMO雷达低空多路径目标检测

巨丹静， 邓洪高， 刘庆华， 孙少帅， 李 哲

(1.桂林电子科技大学 信息与通信学院,广西 桂林 541004；2.石家庄锐创电子科技有限公司,石家庄 050000)

近几年，由于低空空域的开放，越来越多的航模、小型无人机、动力三角翼等类型的目标活动于低空空域。随着这类低空目标的发展，带来的威胁与日俱增，对于低空非合作目标的探测也就至关重要[1]。迄今为止，国内外针对低空目标的检测方法主要包括基于粒子滤波的TBD(track before detect) 技术的检测方法[2]、基于激光防御的检测方法[3]及基于形状特征辅助的检测方法[4]等。以上方法多用于对低空目标图像或视频的处理，而用于雷达探测的方法有PD雷达探测法[5]、基于OFDM的雷达检测法[6]、MIMO雷达低空动目标检测法[7]、OFDM-MIMO雷达低空目标检测法[8]和相控阵雷达低空目标检测法[9]等。当目标飞行高度较低时，多径回波与直达回波无法区分，会导致接收信号时强时弱，因此多路径效应是雷达低空目标检测的一大难题。

自2006年Antonik等[10]提出频率多样化阵列以来，许多学者对其进行了深入研究。与传统相控阵的不同之处在于，FDA在相邻阵元间引入了一个小的频率增量[11]，在空间上形成弯曲的“S”形波束图，扩展了空间自由度。在文献[12]中，FDA被应用于前视雷达对地面运动目标的检测，与传统相控阵雷达相比，可在一定程度上抑制距离模糊杂波。仿真结果也表明，FDA能够将SAR雷达的方位方向和距离方向的成像分辨率提高。Sammartino等[13]将FDA雷达与MIMO雷达技术相结合，提出了具有频率和波形多样性的MIMO雷达概念。它不仅具有MIMO雷达优良的目标检测性能，而且具有FDA雷达的空间自由度。在此基础上，文献[14-15]进一步研究了FDA-MIMO雷达的具体应用，认为FDA-MIMO雷达在旁瓣抑制和目标检测性能方面有较大改善。文献[16]研究了频率增量误差对FDA-MIMO雷达自适应波束形成和目标检测性能的影响，为FDA-MIMO雷达的波形设计提供了理论指导。

鉴于此，将FDA-MIMO雷达应用于低空目标的检测。建立在多径条件下的FDA-MIMO雷达信号发射接收模型，并选择合适的阵列间距。由于接收端多径信号和地球反射面不一致的影响，设置了更适合的频率增量和反射系数，采用广义似然比检测(GLRT)方法对低空目标进行检测。通过理论仿真验证了FDA-MIMO雷达对低空目标检测的有效性。与传统多输入多输出(MIMO)雷达和频控阵(FDA)雷达相比，其检测效果更加显著。

1 FDA-MIMO雷达低慢小目标模型

针对低空目标存在目标闪烁效应和多路径效应的特点，只考虑一阶镜面反射，不考虑漫反射，建立基于FDA-MIMO雷达低空目标多路径信号传播模型，如图1所示。

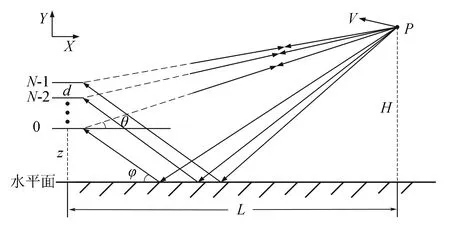
图1 FDA-MIMO雷达低空多路径信号传播模型

图1为一个N×N的均匀线性FDA-MIMO雷达系统，各阵元间距为d，每个收发阵元发射一个载频为fn的信号，n=0,1,…,N-1。设置第0个阵元位于距离水平面高度Z处，假定目标点p位于远场并以恒定的相对速度v运动，v=[vx,vy]表示运动目标的相对速度。目标的高度和目标到阵列的水平距离分别为H和L，目标与阵列法线的夹角为θ，则目标与第0个阵元的径向距离为

目标回波经水平面反射到第0个阵元的距离为

令第n个阵元发射，第m个阵元接收的直达路径信号的传播时间为

反射路径信号的传播时间为

其中，c为在真空中电磁波的传播速度，φ为反射路径回波的入射方向角。若第n个阵元发射，第m个阵元接收的直达路径信号和反射路径信号的多普勒频率分别为fd、fr，则fd、fr与目标速度v的关系可表示为

(1)

(2)

其中,vx、vy分别为目标在坐标轴X、Y方向的速度。针对低空目标，引入Swerling2目标起伏模型，目标在直达路径和反射路径中的散射系数分别为rejφ、ρrejφ。其中：ρ为镜面反射系数；rejφ为目标的散射特性，其与目标的雷达截面积(RCS)有关。令α=rejφ，β=rejφρ，假定发射脉冲信号的幅度为1，由于fd≪f0，fr≪f0，第m个接收阵元解调后的信号可简化为

(3)

对第m个阵元解调后的接收信号ym(t)进行离散采样，令t=τ0+kTPRI，根据发射阵元个数N和一个相干处理间隔(CPI)内累积的脉冲数K，在发射阵元与接收阵元数量相同的情况下，将N×N个收发组合的测量值组成一个N2×1阶列向量，构造回波观测数据矩阵：

(4)

将y(k)写成矩阵乘法形式：

y(k)=Ab(k)+e(k)，

(5)

an=[α,β]T，

是一个2N2×1阶列向量。

(6)

在一个相干处理间隔(CPI)内有K个脉冲做累积，则所有的测量数据可写为N2×K阶的矩阵形式，回波观测数据矩阵Y可表示为

Y=AB+E，

(7)

其中：B=[b(0),b(1),…,b(K-1)]为包含目标多普勒信息的2N2×K阶矩阵；E=[e(0),e(1),…,e(K-1)]为N2×K阶矩阵，包含噪声等其他干扰。

2 FDA-MIMO雷达广义似然比检测

若要实现对低空目标的检测，则需将FDA-MIMO雷达中的回波信号检测看作一个二元假设检验问题。在H0假设下，目标不存在，则散射系数A=0，噪声协方差矩阵S未知；在H1假设下，目标存在，则散射系数A≠0，目标速度v与噪声协方差矩阵S均未知。因此，检测问题可表示为

(8)

构建在高斯白噪声下的二元假设检验问题，并得到无目标和目标存在2种假设下的条件概率密度P0(Y,S0)和P1(Y,S1)，分别表示为

(9)

(10)

其中：S0为无目标时噪声的协方差矩阵；S1为目标存在时噪声的协方差矩阵。

考虑到实际应用情况，采用广义似然比检测(GLRT)方法对低空目标进行检测，而未知参数可通过最大似然估计(MLE)得到。因此，对目标散射系数A的估计步骤为：

1)因为具有块对角结构的散射系数A通常情况下不能得到一个完全封闭的MLE表达式，所以对散射系数A采用AML(近似极大值似然)估计。将矩阵A块对角向量化为向量

AAML=[vec(A11)T,vec(A22)T,…,vec(ANN)T]T。

(11)

2)求向量AAML的最大似然估计

(12)

其中：

G=Y(IK-Π)YH；

Π=BH(BBH)+B；

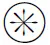
(13)

(14)

假设目标速度v=[vx,vy]已知，对式(7)的GLRT方法就是将无目标和目标存在这2种假设下似然函数的比与门限做比较，可得最终的检测统计量

(15)

其中,τ为似然比检测门限，通过给定的虚警概率计算得到。

3 仿真结果及检测性能分析

1)实验1：假设收发阵元数N=10，目标的雷达散射面积为2 m2，目标相对雷达的运动速度v=[50,0]，仿真结果如图2～5所示。

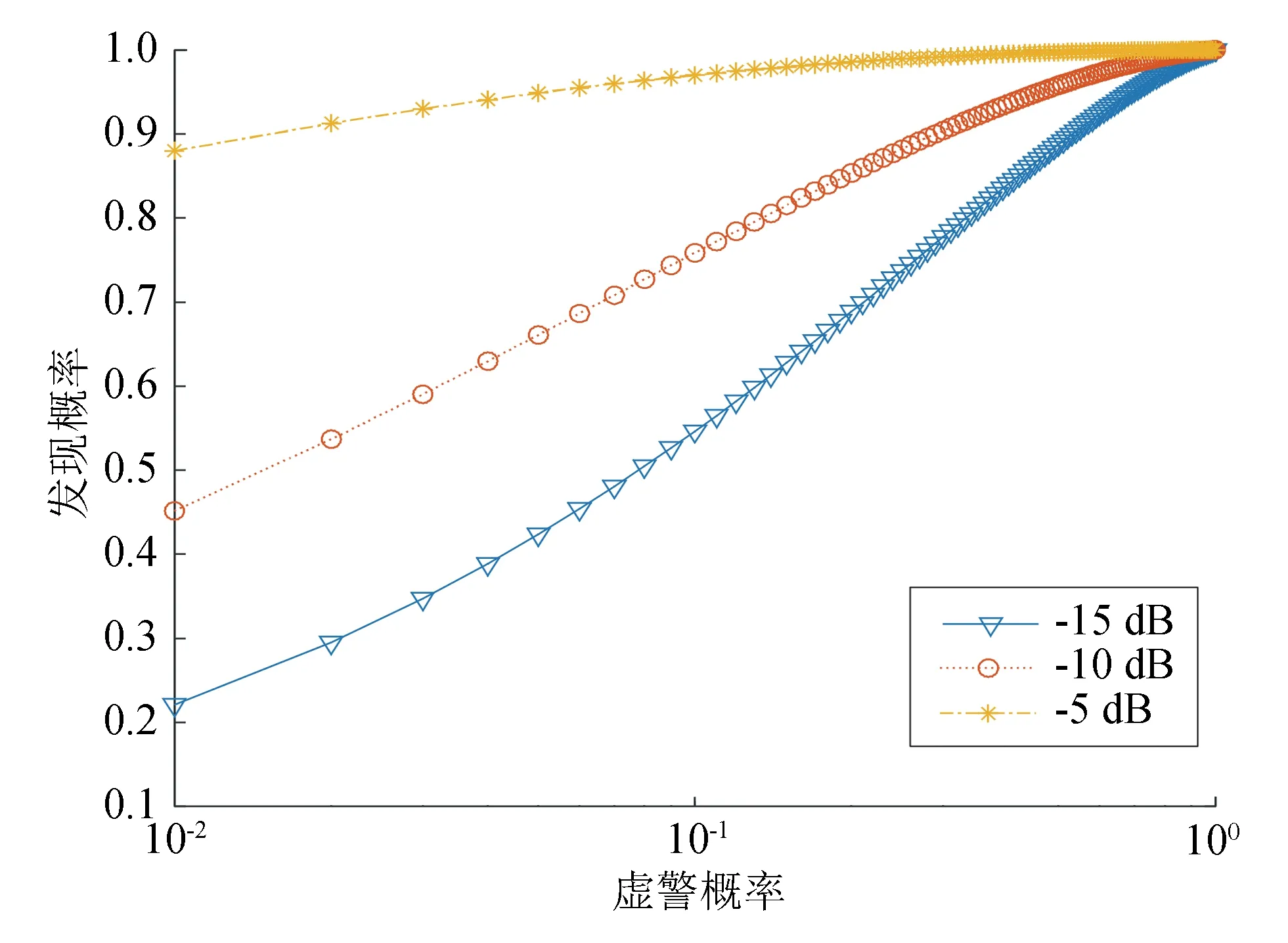
图2 信噪比不同时，发现概率随虚警概率的变化曲线

图3 阵元数不同时，发现概率随虚警概率的变化曲线

图4 目标速度不同时，发现概率随虚警概率的变化曲线

图5 信噪比为-10 dB时，3种方法的检测性能对比曲线

由图2可知，当虚警概率保持10-2不变时，发现概率由0.22提高到了0.88。从图3可看出，当虚警概率为10-2时，N=8的发现概率比N=12的发现概率提高了0.38。因此，雷达的阵元数越多，其发现概率就越高。从图4可看出，当虚警概率为10-2，相对运动速度v从[0,50]变为[50,0]时，发现概率从0.22提高到了0.78。因此，当目标相对雷达的运动方向与直达回波方向之间的角度越小时，接收端回波的多普勒频率越大，同时使得对散射系数的估计更加精确，检测性能也更优。从图5可看出，当虚警概率为10-2时，采用FDA-MIMO GLRT比单独采用FDA GLRT、MIMO GLRT方法时，发现概率分别提高了0.42、0.36。

2)实验2。针对常见的航模、无人机、动力三角翼这3种低空目标分别进行检测。信噪比为-10 dB，雷达的阵元数N=12，相对运动速度v=[0,45]，虚警概率为10-2。由图6可知，动力三角翼的发现概率比无人机和航模的发现概率高。因此，当目标的雷达散射截面积越大，发现概率也越高。

图6 3种不同RCS下发现概率随虚警概率的变化曲线

4 结束语

将FDA-MIMO雷达应用于多径低空环境下目标的检测。采用FDA-MIMO雷达体制得到的测量值个数是采用FDA雷达体制下的N倍，对目标的散射系数估计更加精确，使其对目标的检测性能更高。该方法结合了FDA雷达和MIMO雷达的优势，既能有效地抑制低空多径效应对目标检测带来的影响，也能较好地克服由目标RCS起伏带来的性能损失，从而获得较大的空间分集增益。仿真结果验证了在FDA-MIMO 雷达体制下采用广义似然比检测方法对低空目标具有良好的检测效果。