局部最大核子图搜索算法研究
罗碧彤 孙晶 李源 李欣蔚
(北方工业大学信息学院 北京市 100144)
1 引言
由于图形数据在不同应用中的普遍存在,图形分析已经引起了研究界和行业界的广泛关注。图分析中的一个主要问题是给定一个图,识别图中的内聚子图,如k核,k型桁架,派系,n-派系和n-族。其中,k核能在线性时间复杂度内计算,被定义为无向图G的极大子图,使子图中的所有顶点的度至少为k。社区搜索在社会网络分析中具有重要意义,对于图中给定顶点,目标是找到该顶点所属的最佳社区。直观地说,对于给定顶点的最佳社区应该在顶点附近。Cui等人提出了一种局部搜索策略,即在一个顶点附近进行搜索,以寻找该顶点的最佳社区。大多数现实生活中的复杂网络,包括互联网、社交网络和生物神经网络,都包含了社区结构。网络可以被划分为组,其中连接紧密,组与组之间的连接是稀疏的。在真实的网络中寻找社区是一项重要的分析任务,因为社区结构充满意义,它们与网络的功能高度相关。由于社区结构的重要性,社区搜索的问题,即寻找顶点最可能的社区,对许多现实生活网络和应用十分重要。在信息时代,图的规模变得巨大,图模型所代表的数据中的价值也越来越重要。因此,在大规模图中寻找核数最大的包含查询点的极大连通子图是一个重要且有意义的问题。在探索核数最大的包含查询点的极大连通子图的过程中,从查询点开始向外扩展,其中判断扩展的顶点是否具有提升当前k核的能力是扩展阶段的主要问题。在本文中,提出了Order算法即广度优先搜索,与遍历顶点相连个数和与未遍历顶点相连个数将需要扩展的顶点进行排序,通过Elevate-K算法即core上界和mcd上界判断需要扩展的顶点是否具有提升当前k核的能力,减少了寻找时间,提高了算法的效率。由于在探索最大k核子图的过程中,图是动态的,其中顶点/边将随着判断是否具有提升当前k核的能力被动态地插入/删除。因此,降低图不时动态更新时计算k核的计算成本是更新阶段的主要问题。Lin等人提出了分层核心维护,但本文问题只需要核数最大即可。Zhang等人提出了一种新的基于顺序的方法,在顶点的更新 图之间保持顺序,称为k阶。然而,现有的问题中提出了使用局部搜索策略寻找包含查询点的k核,忽略了核数和规模最大的问题。针对上述问题,首先通过广度优先搜索和最大发生率,将需要探索的邻接点进行排序。然后,基于核数core和最大核心度maximum-core degree(mcd),提出了通过core上界和mcd上界判断顶点是否具有提升当前核数的能力。对于规模最大的问题可以理解为什么时候停止搜索的问题,本文提出通过比较已经遍历顶点的邻接点是否属于被删除的顶点这一特性来判断是否图规模达到最大值,是否可以停止搜索,若条件成立,则当前社区是最好的,停止搜索。为了找到核数最大的包含查询点的极大连通子图:
(1)本文提出了一种全局搜索算法,通过与查询点的度比较,逐步删除度小于查询点度的顶点,称为Global Search-Max K Core(GS-MKC)。
(2)为了提高效率,进一步提出了一种具有扩展-精简思想的局部搜索算法,称为Local Search-Max K Core(LSMKC)。
2 基本概念及相关定义
本节主要介绍一些基本概念及其符号表达,阐述了k核的相关定义,并对要解决的主要问题给出具体定义。
2.1 基本概念
给定G(V,E)为顶点集合为V,边集合为E的无向图。对于任一子集H⊆V,由H诱导出的子图定义为G[H],其中顶点集合为H,边集合为(H×H)∩E。deg(v)表示顶点v在图G中的度,其中G[H]为图G的子图,因此deg(v)≤deg(v)。
定义 1(群体良度):给定G(V,E),其中集合H⊆V,由集合H诱导出的子图G[H]为一个群体。G[H]的群体良度定义为图的最小度:
δ(G[H])=min{deg(v)|v∈H}
其中δ(·)是不单调的,因此δ(G[H]∪{v})并不一定小于δ(G[H])。
定义 2(邻接点):使用nbr(u,G)表示顶点u∈V(G)的邻接点,定义为:
nbr(u,G)={v∈V|(u,v)∈E}
定义 3(群体邻接点):给定图G(V,E),对于集合H⊆V,G[H]的群体邻接点定义为集合H中的顶点与集合H外直接相连的顶点的集合:
nbr(G[H])={v|w∈H,v∈V,v∉H,(w,v)∈E}
定义 4(k核):图G的子图G表示为k核,定义为:(1)对于∀u∈V(G),deg(u,G)≥k;
G是最大的。若图G的k核不存在,则G=∅。对于一个给定的k,图G的k核G是唯一的,并且∀k≥0,G⊊G。当k=0时,G就是图G。
定义 5(核数):对于每个顶点u∈V(G),它的核数core(u,G)定义为:
core(u,G)=max{k|u∈V(G)}
定义 6(core(v,v)):由核数定义可知,在图G中加入点v之后,顶点v的核数可能保持不变,也可能增加,因此core(v,v)定义为在加入顶点v之前,顶点v的核数。
定义 7(最大核度maximum-core degree):顶点u的最大核的度表示为mcd(u),给定w为顶点u的邻接点,mcd(u)定义为具有core(w)≥core(u)性质的邻接点的个数:
mcd(u)=|{w:(u,w)∈E,core(w)≥core(u)}|
定义 8(纯核度pure-core degree):顶点u的纯核度表示为pcd(u),给定w为顶点u的邻接点,pcd(u)定义为具有core(w)=core(u)并且mcd(w)>core(w)性质或者core(w)>core(u)的邻接点的个数:
pcd(u)=|{w:(u,w)∈E,core(w)=core(u)∩mcd(w)>core(w) or core(w)>core(u)}|
定义 9(集合定义):在加入或删除一个节点之后,图中各个顶点的核数有可能发生改变,有的顶点核数增加,有的顶点会确定不在所求图中。因此,定义集合H包含已经遍历过的顶点,集合N包含需要遍历的顶点,集合C包含确定不在所求图中的顶点,集合F记录最终所求图的顶点。集合H的初始顶点为查询顶点v。N=∅,C=∅,F=∅.对于还未遍历过的顶点核数设为无穷大。
2.2 问题定义
基于以上定义,本文给出了在大规模图中发现核数最大的包含查询点的极大连通子图的问题定义。
问题:对于一个图G(V,E)和一个任意顶点v∈V,发现集合H⊆V,其中H具有如下性质:
(1)v∈H;
(2)G[H]是一个连接子图;
(3)δ(G[H])是最大的;
(4)G[H]的顶点数量最多。
接下来的章节,本文具体的阐述Max K Core(MKC)的发现算法。
3 MKC发现算法
本节讲述大规模图中核数最大的包含查询点的极大连通子图发现问题,给定查询点v,从中发现包含查询点v的最大k核。本节将从两方面出发研究探索这一问题,即全局搜索和局部搜索。全局搜索将查询图中每个节点的度,局部搜索从查询点v开始逐层向外扩展,添加具有提升当前k核能力的顶点,淘汰当前不具有提升k核能力的顶点。接下来详细的介绍两种发现算法。
3.1 GS-MKC算法
本小节的GS-MKC算法,是基于从大规模图逐步搜索核数最大的包含查询点的极大连通子图的基础策略,该算法需要遍历图中的所有顶点。
算法1.GS-MKC(G,v)
首先计算查询顶点v的度,逐个将图中度小于deg(v)的顶点删除,并将其邻接点保存在集合中,因为在删除度小于deg(v)的顶点时,其邻接点的度也会受到影响而变化,下一步便检查集合中即邻接点的度是否在删除顶点之后度小于deg(v),若邻接点为查询点v的邻接点则不删除,因为若删除查询点的邻接点,查询点的度会变小,如此一直检查,直到没有顶点可删,得到包含查询顶点v的图即为核数最大的包含查询点的极大连通子图。
输入:图G(V,E);查询顶点v;
输出:核数最大的包含查询顶点v的极大连通子图;
(1)计算查询顶点v的度;
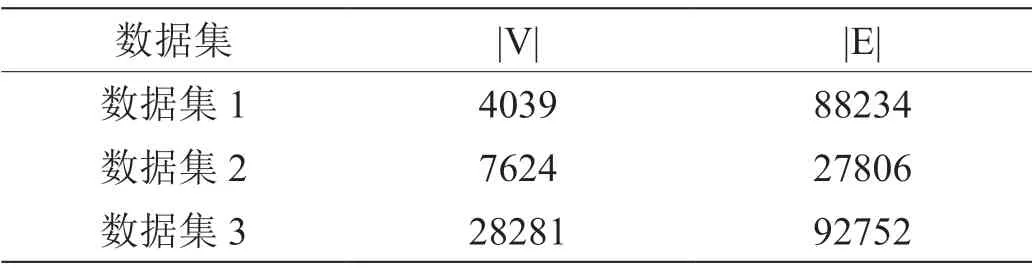
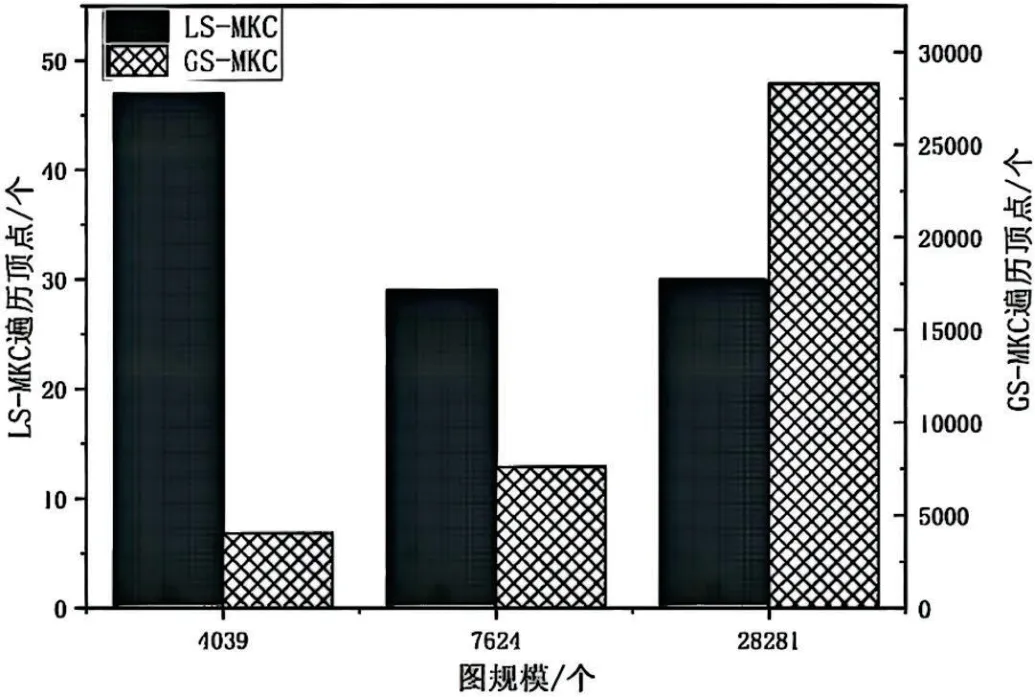
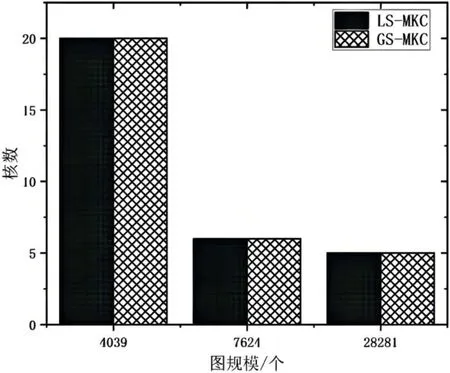
(2)WHILE deg(v) (3)删除顶点v; (4)判断顶点v的邻接点是否小于deg(v); (5)得到包含查询点的最大k核子图。 本节对上一小节的算法进行改进,上一节算法虽然简单,但代价非常昂贵,因为图中的所有顶点都需要访问,在此基础上提出一种优化策略下的LS-MKC算法,从查询点出发,对需要遍历的顶点使用Order算法排序,减少发现时间,提高算法效率,在每次插入顶点之后使用Elevate-K算法将不能帮助提升当前核数的顶点删除,其中,插入/删除顶点之后保持k核采用现有算法提出的k阶,将每个k核保存在k阶之中,顶点在k阶之间变化。 算法 2.LS-MKC(G,v) 从查询点出发,将其邻接点按照优先级排序插入图G’中,插入之后重新将顶点分组,再将需要遍历的顶点插入图中,直到已遍历的顶点集合的群体邻接点小于查询点v的核数且都处于删除集合中,表示群体邻接点已经没有顶点可以遍历,则搜索结束,得到核数最大的包含查询点的极大连通子图。 输入:图G(V,E);查询顶点v; 输出:核数最大的包含查询顶点v的极大连通子图; (1)WHILE F=∅ do; (2)从集合N中取出下一个遍历的顶点; (3)在G'中插入与H集合中顶点有关的边; (4)FOR 集合H中的顶点w IF mcd(w) (5)将顶点输入H集合; (6)将顶点输出N集合; (7)N⇐Order(G,N,v); (8)判断顶点v是否有提升当前k核的能力,若无则删除; (9)判断当前已经遍历过的顶点是否构成核数最大的包含查询顶点v的极大连通子图; (10)返回 G'。 算法 3. Order(G,N,v) 排序算法是对需要遍历的顶点集合进行排序,使顶点按照一定的优先级先后插入图G’中。首先使用广度优先搜索排序,在广度优先搜索的基础上使用功能函数对顶点进行排序,即按照在将该顶点插入图G’之后,顶点的度从大到小排序,表示与图G’连接最紧密的顶点先遍历,最后按照顶点的未扩展节点个数从大到小进行排序,表示与外界连接最紧密的顶点先遍历,因为这样的顶点提升当前k核和扩大图规模的能力更强,由此得到插入顺序。 输入:图G(V,E);需要遍历的顶点集合N;插入的顶点v;输出:有顺序的顶点集合N; (1)广度优先搜索得到需要遍历的顶点,得到集合S; (2)计算集合S中的f值; (3)计算集合S中的deg值; (4)对于集合S的顶点排序; (5)N⇐N+S; (6)返回N。 算法 4.Elevate-K(G,v,core(v,v0)) Elevate-K算法通过core值上界和mcd上界,判断顶点是否具有提升k核的能力。core值上界表示为当前顶点的核数加上顶点未扩展的邻接点,当前顶点的核数表示现在已经确定的核数,未扩展的邻接点表示该顶点提升当前核数的可能性,顶点与外界的紧密程度。mcd上界表示当前顶点的邻接点中核数大于等于该顶点的数量,同样表示该顶点提升当前核数的可能性。若core值上界或mcd上界小于查询点的核数,则表示该顶点不能为提升当前核数提供帮助,应该删除。 输入:图G(V,E);插入顶点v;插入顶点v之前v的核数core(v,v); 输出:顶点v是否具有提升查询点核数的能力; 为了有效的评估提出的算法,本实验用真实的数据集进行评估,数据集的详细统计信息汇总在表1中,其中|V|表示顶点个数、|E|表示时序边数。 表1:统计数据集 本节分析LS-MKC算法和GS-MKC算法的高效性。 由于不同的图规模对算法的高效性有影响,本节将进行不同规模图下算法性能的对比试验,选用遍历顶点个数和运行时间两个指标对算法的高效性进行评价,两个指标的具体概念如下: (1)遍历顶点个数:在算法运行过程中遍历过的顶点; (2)运行时间:本文提出的两个算法的运行时间。 从图1可以看出,通过调整图的规模可以改变发现包含查询点的最大核子图访问节点的数量。对于GS-MKC算法,由于需要图中全部顶点与查询点的度相比较,因此,GS-MKC算法访问的节点数量为整张图的节点数量,而对于LS-MKC算法,只需要从查询点开始遍历部分顶点,通过上界判断顶点是否需要删除,是否需要停止遍历搜索。从图1中可以看出,LS-MKC算法查找包含查询点的最大核子图访问节点的数量远小于GS-MKC算法。从图2可以看出,通过调整图的规模,查找包含查询点的最大核子图的算法运行时间也随之变化,从图中可以看出,对于规模较小的图LSMKC算法的运行时间比GS-MKC算法长。这是因为,对于规模较小的图,GS-MKC算法可以以较短的时间遍历整张图,并且算法只需要计算每个顶点的度即可,而LS-MKC算法会从查询点开始,通过计算mcd,pcd,核数,邻接点来判断是否插入/删除顶点和是否停止搜索,由此发现最大核子图,因此运行时间长于GS-MKC算法。但是,当图规模较大时,GS-MKC算法会因为需要遍历整张图使得运行时间变长,而LS-MKC算法只需要遍历部分顶点,虽然同样需要计算中间值,但是对比GS-MKC算法,运行时间更小。 图1:不同规模下算法发现遍历顶点数量 图2:不同规模下算法运行时间 本节使用包含查询点的极大连通子图的核数来测试我们提出的算法发现MKC子图的有效性。 图3给出了通过改变图的规模,对于某个查询点使用LS-MKC算法和GS-MKC算法发现的包含查询点的极大连通子图的核数。从实验结果可以清楚地看出,对于同一规模图的同一查询点,使用LS-MKC算法和GS-MKC算法,得到的极大连通子图的核数相同,可以得出LS-MKC算法和GS-MKC算法的有效性。总之,从总的实验结果可以看出,LS-MKC算法优于GS-MKC算法。 图3:不同规模下算法发现极大连通子图的核数 本文旨在发现在大规模图中核数最大的包含查询顶点的极大连通子图。提出了基于全局搜索的GS-MKC算法,该算法需要遍历图中的所有顶点,虽然思想简单,但是代价昂贵。因此为了更早地发现核数最大的包含查询顶点的极大连通子图,本文结合顶点的核数core和最大核心度mcd判断顶点是否具备提升当前核数的能力,决定顶点是否被删除以及是否需要停止搜索,提出了基于局部搜索的LS-MKC算法。最后,本文在三个大型真实数据集上进行了大量的实验,以证明提出的算法的高效性和有效性。3.2 LS-MKC算法

4 实验结果与分析
4.1 算法高效性分析

4.2 算法有效性分析
5 结束语

