概率布尔网络的可重构性分析

樊卓优 张雯雯

（河南理工大学电气学院 河南省焦作市 454003）

1 引言

在系统生物学中，布尔网络常被用于描述系统之间的相互作用，并广泛应用于生物学、博弈论和信息学等相关领域中。布尔网络最早被Kaffuman 用来描述基因的动态行为，因为其结构简单，很快得到了广泛关注，并慢慢扩展，引入控制信号得到布尔控制网络，引入切换信号得到切换布尔网络。2002 年，Shmulevich 提出了概率布尔网络(PBN)，其比布尔网络更加复杂，然而能够更好地模拟实际问题。由于缺乏有力的数学工具，布尔控制网络在提出的前几十年发展缓慢，近年来，程代展教授等人提出了矩阵的半张量积概念，其可以将逻辑系统转换为离散时间模型。在此基础上，布尔网络得到了迅速发展。诸如布尔网络的能控性，能观性，可重构性和状态估计，最优控制等问题都得到了有力发展。

布尔网络的可重构性问题对系统的状态估计和状态观测器设计都十分重要。布尔网络的可重构性在文献中被首次提出，并给出了多状态观测器和移位寄存观测器的设计方法。此后，关于布尔网络和布尔控制网络的可重构性和观测器设计有了较多的研究成果，其中文献提出了一种改进的多状态观测器设计，文献进一步阐述了可观性和可重构性之间的关系，推导了显示和递归两种方法，给出了终止条件，并对一般的可重构系统，设计了类龙伯格观测器。文献简要总结了能观性和可重构性的定义和基本判断定理，将可重构性和可检测性联系起来，给出了它们之间的相互关系图。对于切换布尔网络的可重构性，目前也有很多成熟的结果，文献得到了可重构性的四种定义和判断可重构性的充要条件。然而，对于概率布尔网络的可重构性，目前的研究结果较少。其中，文献提出了可重构性的强和弱两种基本定义，并给出了判断系统强弱可重构的条件。文献研究了概率布尔网络的状态估计问题，提出了可检测性的定义，并首次提出了可检测性的测度概念，并通过利用有限自动机的方法设计了状态估计器。与布尔网络和布尔控制网络相比，概率布尔网络的可观性和可重构性问题更加复杂，因为概率的不确定性，状态演化的方向是不确定的，因此使得状态观测器的设计具有一点的困难。目前，对概率布尔网络的可重构性分析和观测器的设计还缺乏一定的成果。

本文主要对概率布尔网络的可重构性进行分析，主要研究内容如下：

（1）利用状态耦合的方法，先将系统的状态分为两类；

（2）首先根据概率布尔网络的周期可重构性定义，给出了新的判断系统周期可重构的条件并把周期可重构与广义可重构进行对比；

（3）接着把系统状态耦合的形式与有限自动机的加权对图形式进行结合，并在此基础了获得了新的系统可重构的判断定理。

2 预备工作和问题阐述

2.1 预备工作

2.2 问题描述

3 主要内容

3.1 状态分析

3.2 周期可重构性

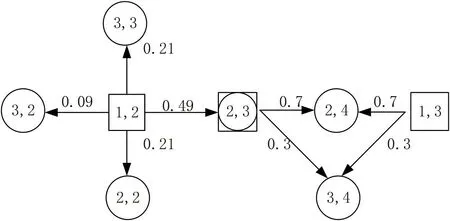
图1： 例1 的加权有向图

3.3 自动机判别法

4 实例验证

下边给出一个例子来简要说明周期判定法的使用过程。

在图2 和图3 中，黑色圆圈中的数字表示输出为的状态，白色圆圈中的数字表示输出为 的状态，实线上的数字代表模型输入结构矩阵和输出序列，例如(1,1)表示结构矩阵为L控制输入为 时的情况，其中一对数字代表有0.25 的概率，即，从状态1 有0.5 的概率转移到状态3。因此，可以得到系统的状态转移图如图2，所有周期状态模型的轨迹图如图3。

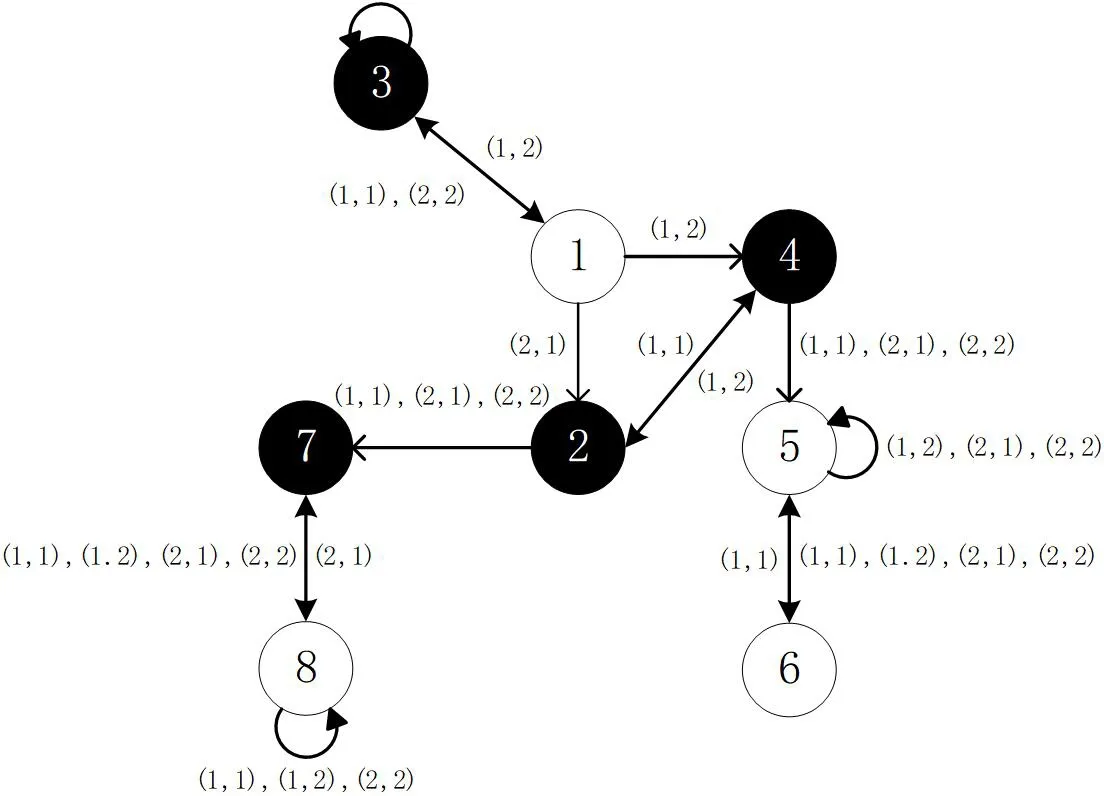
图2： 例2 的状态转移图

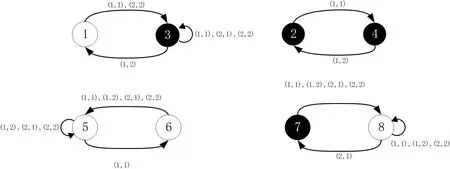
图3： 例2 中的所有周期状态模型输入轨迹

如图3 所示，状态1 和状态5 是一对不可区分的状态对，且有最小相同周期2，但状态1 的下一步状态3 和状态5 的下一步状态6 输出不同，所以状态1 和状态5 是1 步可区分状态。因此根据定理2 可知，该系统是周期可重构系统。同样的，状态2 和状态7 是不可区分状态对，但有最小相同周期2，且是1 步可区分状态。因此由推论1 可知，此系统是R-4可重构的。

因为对不可区分状态对(2,4)和(5,6)，虽然也有最小相同周期2，但在最小相同周期内，其输出都相同。因此由定理1 可知，该状态对不是周期可重构的。

即此系统满足R-4 可重构的条件，不满足R-2 可重构的条件。

5 总结

本文主要对概率布尔网络的可重构问题进行的了分析。首先利用状态对和状态耦合的方法对状态进行了分类，并划分为两个集合；接着针对概率布尔网络的可重构性给出了四种相关定义，并首先讨论了其周期可重构性，给出了判断周期可重构的条件，在第三节中也给出了实例进行验证；最后，利用有限自动机的方法，给出了概率有限自动机的加权对图形式，并在此基础上给出了几个系统可重构的判断定理。然而，概率布尔网络的状态估计和观测器设计仍是研究的重点，这是下一步的主要研究方向。