融合集合经验模态分解与宽度学习的齿轮箱故障预警方法

杨锡运，邓子琦，康 宁

(1.华北电力大学 控制与计算机工程学院，北京 102206；2.华北电力大学 电站设备状态监测与控制教育部重点实验室，北京 102206；3.北京广利核系统工程有限公司，北京 102206)

0 引言

近年来，作为一种清洁、可再生的绿色能源，风能的应用研究得到了快速发展。由于环境恶劣、工况复杂，风力发电机组易发生故障，齿轮箱是风力发电机的重要组成部分，其油温升高易发生齿面胶合等故障[1]。齿轮箱故障导致的停机时间和维护成本在所有类型故障中都非常高，选择一种良好的齿轮箱油温状态监测和故障诊断方法尤为重要[2]。

深层学习思想在数据建模领域已有深度应用，将其与人工智能算法结合，利用运维数据[3]开展基于数据驱动的故障预测研究正成为研究热点[4]。刘辉海等[5]提出一种基于风电机组齿轮箱的数据采集与监视控制(Supervisory Control and Data Acquisition, SCADA)数据和振动信号的深度自编码网络模型，通过所搭建的网络模型智能学习齿轮箱故障前、后深层样本的每一层特征，得到更抽象更高维的数据规则与分布特点。风电机组状态检测过程中数据量大、故障特征提取困难，针对该问题，刘秀丽等[6]提出一种基于深度信念网络的风电机组齿轮箱故障诊断方法，证明在风机故障诊断问题中，与深度置信网络(Deep Belief Networks, DBN)、反向传播神经网络(Back Propagation Neural Network, BPNN)算法和传统故障诊断方法相比，该方法利用深度学习理论的强大感知与自我学习能力能够提高故障诊断准确率。ZHONG等[7]将卷积神经网络与其他人工智能算法结合，取得了较好的效果，其中卷积神经网络用于降低数据规模和复杂程度，提升模型整体的泛化和学习能力。深层结构虽然如此强大，但是由于涉及大量超参数和复杂的结构，使得大多数模型训练时间长，而且预警的准确率与模型精度的关系较大。经验模态分解作为时频分析的一种方法，可用于分析振动信号，常被用于诊断风机故障[8-10]，集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)是其中的一种改进算法。王红君等[11]提出一种基于EEMD小波阈值去噪和布谷鸟算法优化BP(back propagation)神经网络的故障诊断方法，其通过采用EEMD分解和小波阈值去噪方法对故障振动信号进行数据预处理来抑制原始振动信号中的噪声干扰，实例仿真表明,所提故障诊断方法具有良好的诊断精度、速度和成功率；顾煜炯等[12]提出一种基于改进的多元离群监测方法来解决早期故障诊断，该方法较原始方法能够更早地察觉风电齿轮箱的早期故障，但是存在运行工况波动和故障特征不易提取的问题。上述经验模态分解方法在风机故障诊断中的应用均基于振动信号进行。

本文基于风电机组齿轮箱SCADA系统所得的数据样本，提出基于交叉熵融合EEMD变点检测与宽度学习系统(Broad Learning System, BLS)的齿轮箱温度预警方法。首先分别用EEMD和BLS算法为齿轮箱油温建立监测模型。EEMD对齿轮箱油温时间序列进行时频分析，将齿轮箱油温信号分解为多个本征模态函数(Intrinsic Mode Function, IMF)分量，计算健康样本与待测样本的马氏距离[13]；BLS模型对稳定运行状态下的SCADA数据样本进行学习，建立齿轮箱温的状态监测模型，并计算待测样本经模型预测所得的预测油温曲线与真实曲线的关联程度。然后通过计算交叉熵分别评价两个监测模型，得到两个模型的权重，按照权重将两个模型结合，以充分利用时频和相关变量信息，降低误报的可能性，提高故障报警准确率。

1 集合经验模态分解变点检测

1.1 经验模态分解算法

经验模态分解(Empirical Mode Decomposition, EMD)是一种自适应数据信息挖掘方法，其将非线性序列信号分解为若干不同尺度的IMF分量和1个残余分量，从而更加直观地观察信号中各频率分量的分布情况[14-15]。EMD分解信号不需要事先预定或强制给定基函数，而是依赖信号本身特征自适应地进行分解，理论上可以应用于任何类型的时间序列信号。

1.2 集合经验模态分解算法

EEMD是在EMD基础上的改进算法，EMD中的信号极值点会影响IMF，在分布不均匀时会出现模态混叠。EEMD将白噪声引入待分析信号中，白噪声的频谱均匀分布，使不同尺度的信号自动映射到与背景白噪声相关的适当尺度上，从而解决了EMD中极值点分布不均匀导致的所分解信号频率模式混叠现象。算法流程如下：

(1)在原始信号上添加一个白噪声序列。

(2)采用EMD将添加了白噪声的信号分解为多个IMF分量和1个残余分量。

(3)多次重复(1)和(2)，但是每次采用不同的白噪声序列。

(4)获得分解的相应IMF分量和残余分量。

(5)对多次添加白噪音后分解得到的IMF分量和残余分量进行平均计算，得到最终的多个IMF分量和1个残余分量。

1.3 EEMD变点检测在齿轮箱油温上的应用

采用EEMD对齿轮箱油温信号进行时频分析。EEMD将健康样本分解为n个IMF分量，以这n维分量作为基准特征值，计算待测样本的特征值与基准特征值的马氏距离，用于判别齿轮箱的健康程度。

(1)

式中：d1为待测样本与健康样本的马氏距离；xi为待测样本特征值；μ为健康样本基准特征的均值；T为协方差。马氏距离d1越大，该样本的时频特性与健康样本差别越大，该样本的故障概率越大。

为了更好地评估设备的运行状况，进一步通过隶属度函数计算待测样本的健康度，本文选取logistics函数作为隶属度函数，具体为

(2)

式中：f1为样本健康度;k与a为模糊因子。f1越接近1，健康度越高。

2 基于宽度学习网络的故障预警

BLS算法是一种不需要深度学习结构的高效增量学习算法[14]，其主要设计思想是将输入数据的映射特征作为随机向量函数链接神经网络(Random Vector Functional Link Neural Network, RVFLNN)的输入。

风机运行过程中，齿轮箱会不断老化，导致齿轮箱油温的模型特性发生改变，当更新或增加输入数据时，不同于深度学习需要重新训练网络模型，BLS可以通过增量式学习在线更新网络模型，因此实时性好，训练速度快。

2.1 宽度学习的模型结构

BLS网络模型由输入数据、特征节点、增强节点和模型输出组成。其中，特征节点利用输入数据映射得到；增强节点由映射的特征乘随机生成的权重经非线性函数变换得到。将所有映射的特征节点和增强节点直接连接到输出端，得到模型的输出。假设输入的数据集为X，则特征节点

Zi=φ(XWei+βei),i=1,…,n；

(3)

式中：φ为激活函数；Wei，βei为随机生成的第i个特征节点的权重；n为特征节点个数。

增强节点

Hj=ξ(ZnWhj+βhj),j=1,…,m。

(4)

式中：ξ为激活函数；Whj，βhj为随机生成的第j个增强节点的权重；m为增强节点个数。

将特征节点和增强节点作为输入，得到输出矩阵

(5)

(6)

系统模型如图1所示。

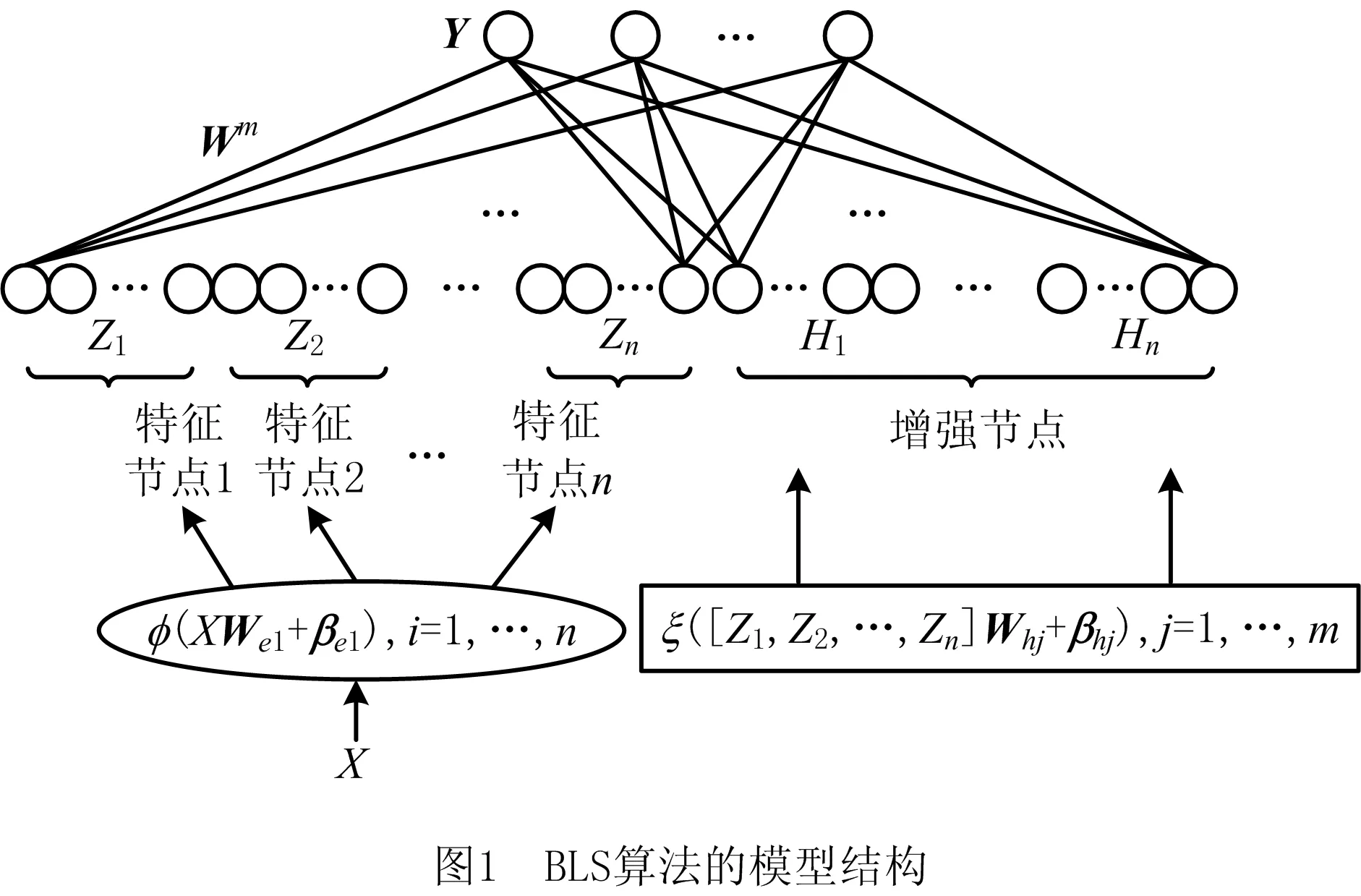
2.2 宽度学习模型的增量式学习

随着机组运行时长的增加，其运行特性会产生变化，使得原始模型不能很好地拟合机组的运行情况。为了使模型更好地适应现场变化，需要在深层结构网络中重新进行训练。当需要提高模型精度时，一般做法是增加训练层数重新训练，训练层数越多，训练时间越长。然而当现场机组运行特性变化或拟合精度不足时，BLS算法不用重新训练模型，只要在训练好的模型基础上在线更新参数即可，同时增量式学习可通过增加特征节点和增强节点的个数，即增加算法的宽度，来提高模型训练的精确度。

图2所示为BLS增量式学习模型，其模型结构使得无论离线建模还是在线更新，均能在实现一定精度的同时保证快速性，更加适应现场需求[16]。

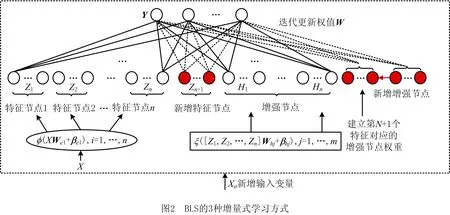
以增加输入数据为例说明BLS增量式学习方式的特点。

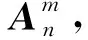
(7)

式中：Zn，Hm分别为原始数据的特征节点和增强节点。

Ax=[φ(XaWe1+βe1),…,φ(XaWen+βen)|

(8)

(9)

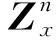
(10)

(11)

式中:

(12)

(13)

(14)

结合式(10)～式(14)，将输出矩阵的权重更新为

(15)

当系统有新的数据输入时，深度学习的模型结构往往需要重新训练整个模型。而对于BLS，由于其横向扩张的独特结构，无需对整个模型进行重新训练，大大提高了计算效率，使在线学习成为可能。

2.3 宽度学习在齿轮箱油温超温故障检测中的应用

用健康运行状态下的齿轮箱数据对BLS网络进行训练，得到齿轮箱油温检测模型，再将待测数据送入训练好的模型中。用模型预测曲线与真实数据曲线的欧式距离和余弦相似度表征两种温度的距离和趋势，从而计算预估值与实际值之间的关联程度。联合二者的欧式距离和余弦相似度表征齿轮箱的健康度。健康度f2的计算公式如下：

(16)

(17)

(18)

(19)

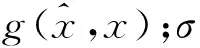
3 基于交叉熵融合的齿轮箱油温预警方法

在机组健康情况下，风机机组的齿轮箱油温一般根据运行状况的不同在30 ℃～70 ℃间波动，当机组齿轮箱出现故障时，齿轮箱的油温会在短时间内升高至75 ℃甚至80 ℃以上。因此，该类故障在提高算法准确性的前提下，应重点考虑检测的及时性、快速性指标。

风机齿轮箱油温会随运行风速、运行功率的随机波动进行不规则变化，呈现出非平稳时间序列特点。EEMD变点检测方法可对温度时序信号进行数据预处理，将信号分解降维成多个序列，从而降低系统的非平稳特性，提高算法的准确性。然而，在机组启停或风速突变时，温度的变化情况可能与风机设备故障的升温情况相似，从而使模型出现误判。而且EEMD作为变点检测方法，在检测过程中只针对监控数据中某一变量进行分解，没有充分挖掘其他变量的信息。

与EEMD相比，作为一种新型算法，BLS能够充分挖掘SCDAD数据中的多维变量信息来判断齿轮箱的健康状况。在快速性方面，相比深度学习网络，BLS有很大的优势。除此之外，由于设备的运行状况会随使用年限发生变化，BLS独特的增量式学习方式使其能够以较小的计算成本不断增加训练数据，以通过更新设备的模型来反映设备状况的真实性，但是BLS需要一定数据量才能保证预测精度，而且其泛化能力不如深度学习[17]。因为BLS网络没有记忆，而温度变化却具有很强的时间连贯性，所以仅采用BLS算法进行故障预警也可能出现误报点。

为了提高故障预警的准确率，本文提出基于交叉熵(cross entropy)融合EEMD与BLS的齿轮箱故障预警方法，该方法能够兼顾准确性和快速性，具体工作流程如图3所示。

3.1 交叉熵

交叉熵是Shannon信息论中的一个重要概念，主要用于度量两个概率分布间的差异性信息。交叉熵用于在给定的真实分布下，衡量使用非真实分布所指定的策略消除系统的不确定性所需要付出的成本。交叉熵越小，预测模型的精度越高。计算公式为

(20)

式中：N为样本数；M为类别的数量；yc,n为第n个样本的指示变量，若该样本为c类别则yc,n=1，否则yc,n=0；pc,n为第n个样本属于类别c的预测概率。

3.2 基于交叉熵融合的温度趋势分析的步骤

基于交叉熵融合的温度趋势分析方法步骤如下：

(1)采用EEMD对健康运行的齿轮箱油温时序信号进行分解，将其分量作为基准特征。计算待测样本分量特征与基准特征的马氏距离，通过式(2)计算待测样本的健康度f1。

(2)利用皮尔逊相关分析筛选出SCADA数据中与齿轮箱油温相关性高的数据作为输入变量，采用BLS建立齿轮箱健康状态下的温度模型进行温度预测。当齿轮箱工作异常时，油温偏离预测值，BLS温度模型预测曲线的分布特性发生改变。将预测曲线与真实曲线的关联程度作为齿轮箱健康度f2。

(3)为了提高预警信息的时效性和准确率，分别用交叉熵评价两个算法所得模型。由交叉熵得到两种算法的权重，按权重将两种算法的健康度结合。当健康度低于阈值时，提示运行人员检查设备状态，以避免机组造成不可逆转的损害，同时为运行人员在突发故障导致停机之前争取更多时间，避免因突发故障停机造成巨大的经济损失。

4 算例分析

本文用安徽某风电场1.5 WM风机2019年6月1日～7月21日的SCADA数据为健康样本，采样间隔为10 min，共8 668个样本，以该机组8月1日至停机前的976个样本数据为待测样本进行仿真。仿真实验基于MATLAB2019a环境，处理器主频为2.5 Hz，内存为16 GB。

4.1 基于EEMD的齿轮箱油温变点检测

齿轮箱油温信号具有不平稳、波动性大的特点，为此本文基于信号尺度分解降维的思想，采用EEMD的方法建立模型，有效处理了非线性时序油温信号。健康机组的齿轮箱原始油温时序信号如图4所示。

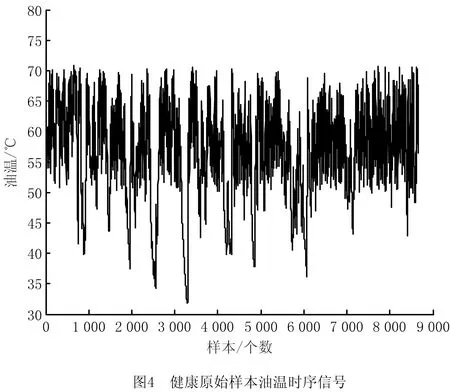
首先进行EEMD分析，根据经验和相关参考文献，所添加的噪声与待分析信号的标准偏差之比为0.2，噪声组数为100。首先对健康样本进行EEMD分解得到基准的特征向量，再对待测样本进行EEMD分解得到待测样本的特征向量，用式(1)计算待测样本与健康样本的马氏距离，通过隶属度函数式(2)，得到该样本的健康度f1，仿真结果如图5所示。

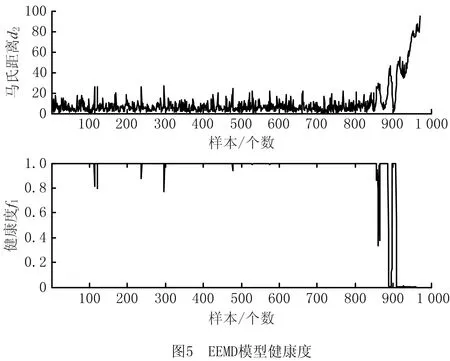
由图5可见，停机前EEMD模型所得马氏距离远大于健康运行状态下的样本，EEMD能够检测出异常温升。

4.2 基于BLS模型的齿轮箱状态监测分析

为了简化输入数据，从SCADA数据中选取与齿轮箱油温相关性强的变量作为模型的输入变量。本文引入Pearson相关系数[18]，将齿轮箱油温作为参考变量，系数的值域为[-1,1]，系数值越大，相关性越强。相关系数

(21)

根据式(21)计算变量与油温之间的相关系数，得到的结果如表1所示。

表1 相关性分析结果

由相关性分析得到模型的输入为齿轮箱高速轴驱动端轴承温度、齿轮箱高速轴非驱动端轴承温度、发电机非驱动端轴承温度、风速、风功率5个变量。

选取风电机组健康运行过程中的齿轮箱样本数据与算法拟合效果进行对比，测试样本数量为500。将BLS算法与BP神经网络、支持向量机(Support Vector Machine, SVM)和DBN进行对比仿真，采用平均绝对误差MAE、均方根误差RMSE、训练时间T作为算法的性能指标来比较拟合结果。其中：BP的网络结构为5-15-1；SVM选用多项式基核函数作为核函数；DBN网络结构为5-20-15-1，激活函数为sigmoid函数；BLS增加训练样本的方式为增量学习，具体公式如2.2节所述，特征节点的数目为50，激活函数选用线性函数；增强节点数为200，激活函数选用tansig函数。采用同样的训练数据和测试数据对所得测试集拟合结果进行分析，仿真结果如表2所示。

表2 算法性能对比

由表2可见，在训练数据样本较少时，BLS预测精度相比BP,SVM,DBN较低，但是当训练数据逐渐提升至7 000及以上时，BLS的预测精度优于BP，SVM，DBN，而且BLS的训练速度远快于其余3种算法。这是由于其特殊的增量式学习方式大大缩短了计算时间，以训练数据8 000为例，因为BP，SVM，DBN无法直接进行增量式学习，所以需要每次重新训练所有样本，即BP，SVM，DBN需要用全部8 000个数据重新训练其权值，从而耗费了大量时间。而BLS只需要对新增的1 000个样本进行增量学习，当训练数据为8 000时，其仿真总训练时间为训练数据7 000时的训练时间加上本次增量学习所用的时间，极大加快了运算速度，使其在工业应用上更具可行性，因此将其作为一种温度预警模型算法进行后续应用是有效的。

根据2.3节所述，将停机前的976个待测样本送入训练好的BLS模型中，得到预测油温，然后根据式(15)计算待测样本的健康度。所得预测结果拟合情况及待测样本的健康度如图6所示。

从图6可见，在机组健康运行状态下，各SCADA状态监测变量之间满足稳定的内部联系，处于动态平衡状态。当齿轮箱状态健康时，这种动态平衡表现为，真实值和预测值的关联程度虽然存在一定波动，但是保持相对稳定；当齿轮箱发生异常时，状态监测变量间失去长期稳定关系，反映齿轮箱油温状态的健康度随之下降。

4.3 基于交叉熵的算法融合

采用交叉熵分别对两种算法模型进行评价。由于故障检测问题是二分类问题，采用交叉熵公式

(22)

计算EEMD与BLS两种模型的交叉熵，其中EEMD方法所得交叉熵为0.103 2，BLS方法所得交叉熵为0.149 2。交叉熵值越低，模型越准确。因此以两种算法的交叉熵为各自权重进行融合，计算公式如下：

(23)

f=ω1·f1+ω2·f2。

(24)

式中：L1，L2分别表示EEMD模型和BLS模型得到的交叉熵；f1，f2分别表示EEMD模型和BLS模型得到的健康度。

为了验证基于交叉熵进行算法融合后的方法在齿轮箱故障预警问题上的效果，对EEMD模型所得样本健康度、BLS模型所得样本健康度及基于交叉熵融合后的方法所得的样本健康度进行对比，对比结果如图7所示。

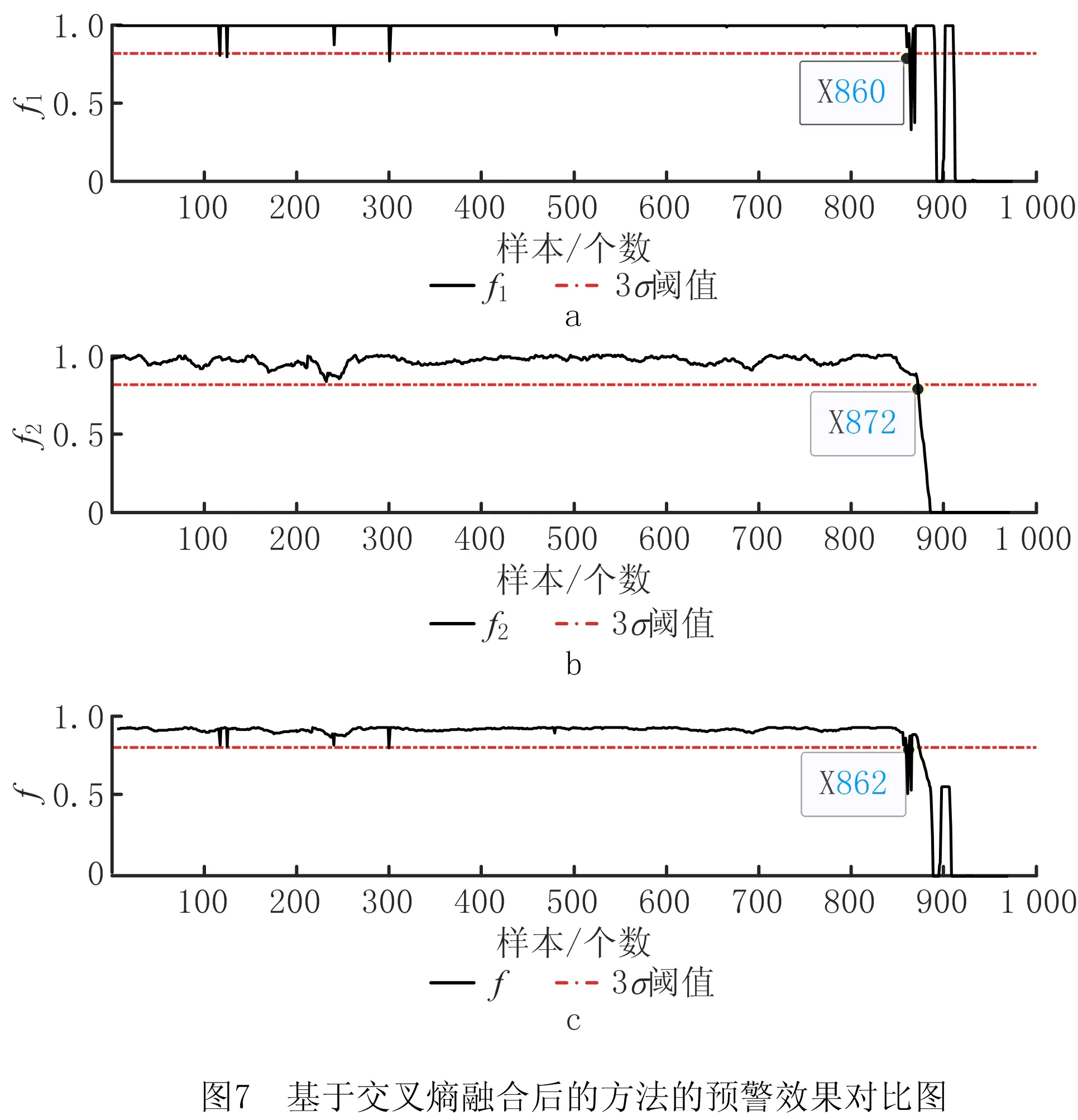
以3δ定律确定正常状态下的健康度阈值，如图7中的虚线所示。由图7可见，EEMD模型所得的健康度f1在860点低于阈值，因此能在停机点前116点给工作人员发出预警信号。然而因为风速不确定导致风机启停不确定，风机启停时的温升变化特性与故障时相似，所以启停时容易出现误报，图7a的f1在第120个数据点和第291个数据点时都超过了阈值。图7b BLS模型所得的健康度f2在第872个数据点时低于阈值，即在停机点前104点发出预警信号，比EEMD模型所得预警结果延迟了12个数据点，而且当机组健康运行时健康度f2也会出现波动。而融合后的健康度f能够避免f1的误报点，同时减小f2的波动性，并可在停机前114点发出预警信号，提醒运行人员关注该机组的运行状况。

为验证融合方法对齿轮箱超温预警的可行性，搜集同个风场不同机组的数据，以3∶1的比例选取健康样本和故障样本进行仿真。用EEMD模型预警方法、BLS模型预警方法对比本文所提的融合方法，仿真结果如表3所示。可见，融合后的方法的提前预警时间高于BLS方法，略低于EEMD方法，且准确率高于单种方法。

表3 故障预警效果对比

4.4 基于融合方法的故障分析

为进一步探究齿轮箱超温故障的原因，针对前文所述停机故障，以6月1日～7月21日的8 668个健康样本为训练数据，停机前的976个待测样本为测试数据，将齿轮箱油温、发电机非驱动端轴承温度、发电机非驱动端轴承温度、风速、功率作为BLS模型输入，齿轮箱高速轴驱动端轴承温度、齿轮箱高速轴非驱动端轴承温度作为输出，其他步骤不变，用融合方法分析超温故障，得到驱动端轴温与非驱动端轴温的健康度，仿真结果如图8所示。

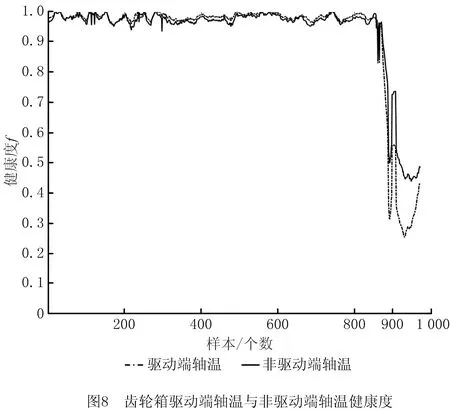
由图8可见，在本次齿轮箱油温超温停机故障中，驱动端轴温健康度下降的幅度明显大于非驱动端轴温健康度，提示该齿轮箱油温超温故障可能由驱动端轴承引起，为后续工作人员登塔处理提供了检修方向。

5 结束语

针对风力齿轮箱的状态监测与故障诊断方法研究，本文提出采用交叉熵将EEMD变点检测方法和BLS算法融合进行故障预警的方法，实现了基于SCADA运行数据趋势的齿轮箱温度早期预警。利用交叉熵确定两种故障模型的权重，对两种算法进行融合，通过实际故障分析验证了融合后的方法在风机故障预警问题中的有效性，即降低了单种方法的误报概率，提高了预警准确性，而且训练速度快、计算量小。由于该融合方法应用算法自动对信号进行数据挖掘分解，其原理具有通用性，可以进一步推广到风机其他关键部件(如主轴承和发电机等)的故障诊断与预警中。

后续的研究重点为提高BLS算法的预测精度，并对该融合方法在风机齿轮箱以外其他设备的故障诊断与预警问题中的应用进行仿真验证。