基于非线性干扰观测器的解耦时变快速终端滑模控制
杨光宇,陈思溢,王雨轩,郑贝阳,黄辉先
(湘潭大学 自动化与电子信息学院,湖南 湘潭 411105)
0 引言
欠驱动机械系统(Underactuated Mechanical Systems, UMS)指独立的控制输入维数少于系统自由度的一类系统[1],其结构简单,同时由于系统高度非线性、参数扰动及控制量受限等,欠驱动系统又足够复杂,适合于研究和验证各种算法的有效性[2];当全驱动系统的部分驱动器出现故障时,系统相应变为欠驱动系统,欠驱动系统控制算法可以进行容错控制。鉴于现实生活中的很多系统均以欠驱动形式存在,如移动机器人、航天飞行器、倒立摆等[3],针对欠驱动系统的研究具有重要的理论与实际意义。
欠驱动系统领域研究比较复杂的原因是执行器的数量少于需要控制的自由度,许多传统非线性控制方法并不适用,近年来主要用基于反馈线性化[4]、能量法[5]、反步法[6]、滑模控制法[7-8]和模糊逻辑法[9]等方法进行UMS稳定控制[10]。滑模变结构控制系统算法简单,对干扰和未建模系统状态具有很强的鲁棒性,且响应速度快,本文主要讨论滑模控制方法。
滑模控制(Sliding Mode Control, SMC)本质上是一类特殊的非线性控制,其不连续的开关特性使系统抖振不可避免,影响了系统性能,如果处理不当,则可能引起系统不稳定。因为滑动模态可以进行设计而且与控制对象的参数和扰动无关,所以SMC具有响应速度快、鲁棒性强、对参数变化和扰动不灵敏等优点[11]。其中,抖振为SMC系统中普遍存在的问题,消除抖振会使变结构控制失去对干扰和摄动的抑制能力,而且无法完全消除,只能对其进行削弱。如何在削弱抖振的基础上尽可能提高滑模面的趋近速率,是目前滑模控制领域重要的研究课题[12]。
SMC采用线性滑模面,系统状态在接近平衡点时的收敛速度非常慢且收敛时间不能确定[13],为此,终端滑模控制(Terminal SMC, TSMC)在传统滑模面函数的基础上加入分数指数项,当系统状态到达滑模面后,将沿设计的指数规律逐渐趋近于平衡点,从而保证系统状态在有限时间内收敛[14-15]。然而,当系统状态到达原点后,由于非线性项中存在负数幂,传统TSMC的控制律出现奇异性,导致控制律无界,而且系统状态远离平衡点时收敛速度较慢。为了提高传统TSMC的收敛速度,杨俊起等[16]结合传统滑模控制的优点,在TSMC滑模面函数中加入线性项,提出快速终端滑模控制(Fast TSMC, FTSMC)方法,提高了系统状态远离平衡点时的收敛速度,具有更好的收敛性;MOBAYEN[17]提出不同形式的FTSMC,对滑模函数中指数项的取值更灵活,但因需要同时考虑系统状态在各阶段的收敛速度而对指数项的取值有所限制,制约了收敛速度的进一步提升。
上述TSMC通常应用于二阶系统,而强耦合的复杂四阶欠驱动系统为二自由度,由于其独立控制输入少于自由度,无法构造单一的控制量使欠驱动系统的所有状态变量都趋于稳定,直接使用上述方法不能获得相同的控制性能。例如,在小车倒立摆系统中,摆杆摆角状态和小车位置状态存在耦合,直接使用TSMC可以成功控制摆杆或小车位置,但若要求同时对二者进行精准控制,则控制效果不佳。为了解决这类问题,解耦终端滑模控制(Decoupled TSMC, DTSMC)通过将一类四阶系统解耦为两个二阶子系统,并分别设计终端滑模面,再通过中间变量构成一个整体滑模面,构造了一个单一的控制量,实现了对小车倒立摆系统的稳定控制[18]。
时变滑模面(Time-Varying Sliding Surfaces, TVSSs)解决了一般滑模面函数参数取值的局限性,可以同时考虑系统状态在各个阶段趋近的情况,并能够显著缩短到达阶段的趋近时间。BAYRAMOGLU等[19]和YORGANCIOLU等[20]根据模糊规则,用模糊规则库导出的线性函数重新定义了SMC滑模面坡度,提高了系统整体趋近速率,并结合快速终端滑模,用解耦方法完成了对四阶系统的稳定控制。
综上所述,TVSSs虽然解决了四阶系统的耦合问题并提高了趋近速率,但是其小车位置状态响应速率很慢。根据快速终端滑模的结构形式,由于其指数项参数选择的局限,限制了系统的趋近效率,本文提出一种变幂次的时变快速终端滑模,通过设计一个非线性函数代替快速终端滑模的指数项,解决参数选取的局限性,提高系统状态在各时刻的趋近速率,同时结合解耦算法,处理系统的强耦合性;针对系统参数的不确定性以及外部干扰对控制效果的影响,设计一个非线性干扰观测器,通过将观测到的总体干扰补偿给控制器来提高控制器的鲁棒性。与现有解耦方法相比,所提基于非线性干扰观测器的解耦时变快速终端滑模控制(Decoupled Time-Varying Fast Terminal Sliding Mode Control based on Non-linear Disturbance Observer, NDODTVFTSMC)策略具有更快的瞬态响应与更低的绝对误差积分准则(Integral of Absolute value of Error criterion, IAE)和时间乘绝对误差积分准则(Integral of Time multiplied by the Absolute value of Error criterion, ITAE)值。
1 问题描述
本文考虑的四阶欠驱动系统以一级小车倒立摆系统为例,可以建模为如下形式[19,21-22]:
y=[x1(t),x3(t)]T。
(1)
式中:x(t)=[x1(t),x2(t),x3(t),x4(t)]T为系统状态向量,x1(t),x2(t),x3(t),x4(t)分别为摆杆角度、摆角角速度、小车位置和小车速度;y=[x1(t),x3(t)]T为系统的输出向量,本文考虑系统的摆角和小车位置;f1(x),f2(x),b1(x),b2(x)为系统动态特性的非线性函数,且均不等于0;u(t)为控制输入;d1,d2为系统的外部扰动。考虑到系统参数的不确定性,有:
f1(x)=f01(x)+Δf1(x);
f2(x)=f02(x)+Δf2(x)。
(2)
式中:f01(x)和f02(x)为函数的已知部分;Δf1(x)和Δf2(x)为函数的未知部分。故式(1)的动态方程为:
(3)
式中:n1=Δf1(x)+d1,n2=Δf2(x)+d2,表示系统整体扰动,包括系统参数的不确定性和系统外部扰动。
一级小车倒立摆系统只有一个控制输入u(t),为单输入多输出系统,且具有强耦合特性。在耦合的情况下,若使用TSMC方法直接控制系统,则分别使系统状态x1(t),x2(t)或x3(t),x4(t)在有限时间内趋近平衡点,这意味着控制输入u(t)只能精确控制摆杆或小车,不能同时使两者保持稳定。
TSMC直接应用于四阶欠驱动系统时,其控制效果不能满足实际要求,而应用于二阶系统则具有优越的控制性能,因此研究终端滑模首先考虑二阶系统。对于小车倒立摆系统,若只考虑摆杆或小车,不失一般性,则可将式(1)表示为如下规范形式的二阶非线性系统:
(4)
式中:x(t)=[x1(t),x2(t)]T为系统状态向量;f(x),b(x)为系统动态特性的非线性函数,且均不为0;u(t)为控制输入;d为外部干扰。
2 二阶系统的新型快速终端滑模控制
2.1 变幂次快速终端滑模控制
针对非线性二阶系统(式(4)),本节不考虑干扰对系统的影响,取d=0。文献[23]提出的FTSMC由以下滑模面描述:
s=αx1+x2+λ|x1|p/qsgn(x1)。
(5)
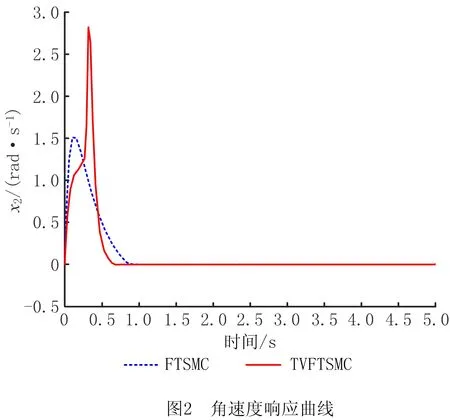
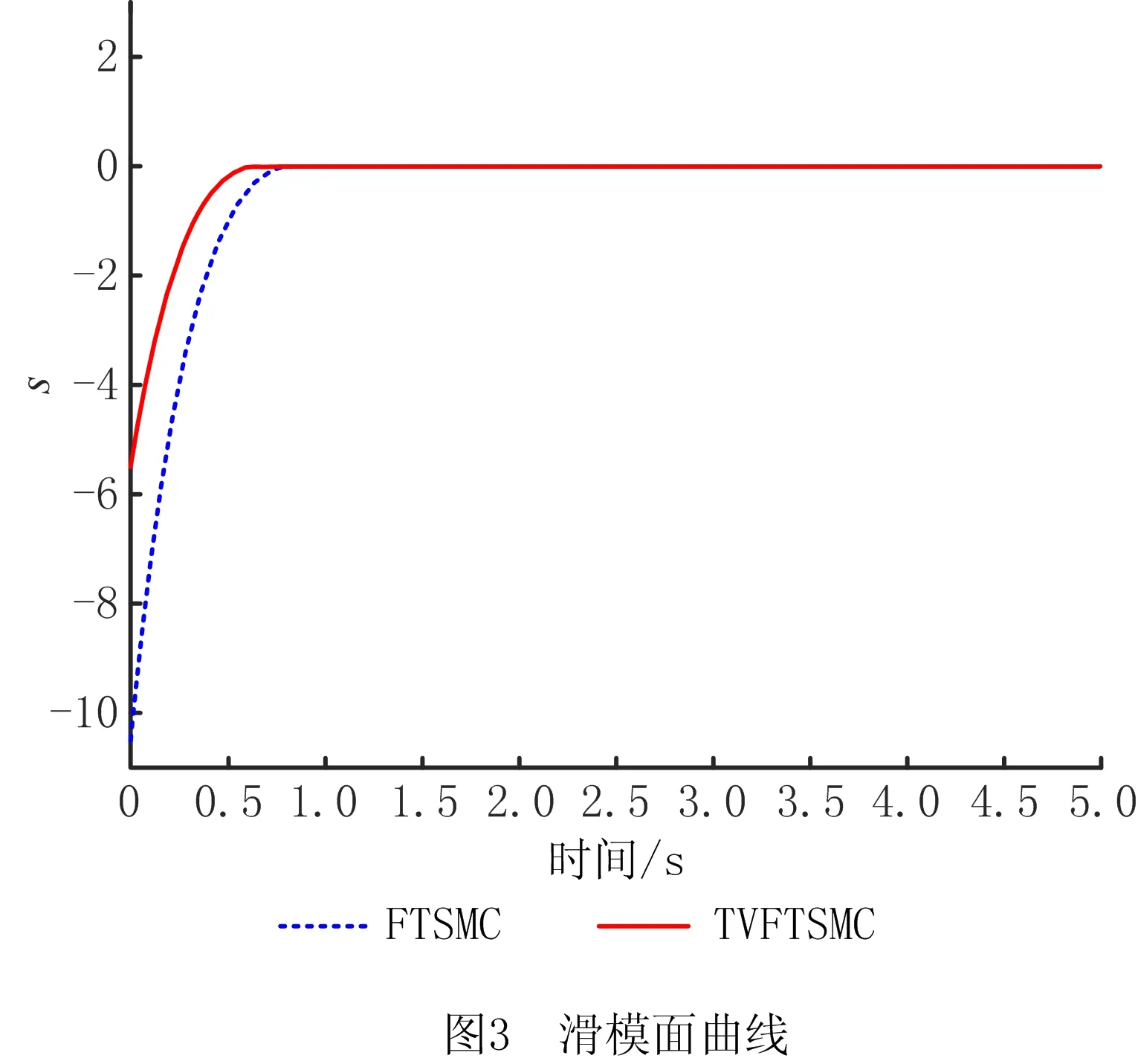
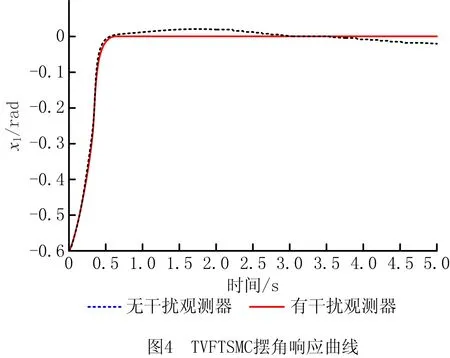
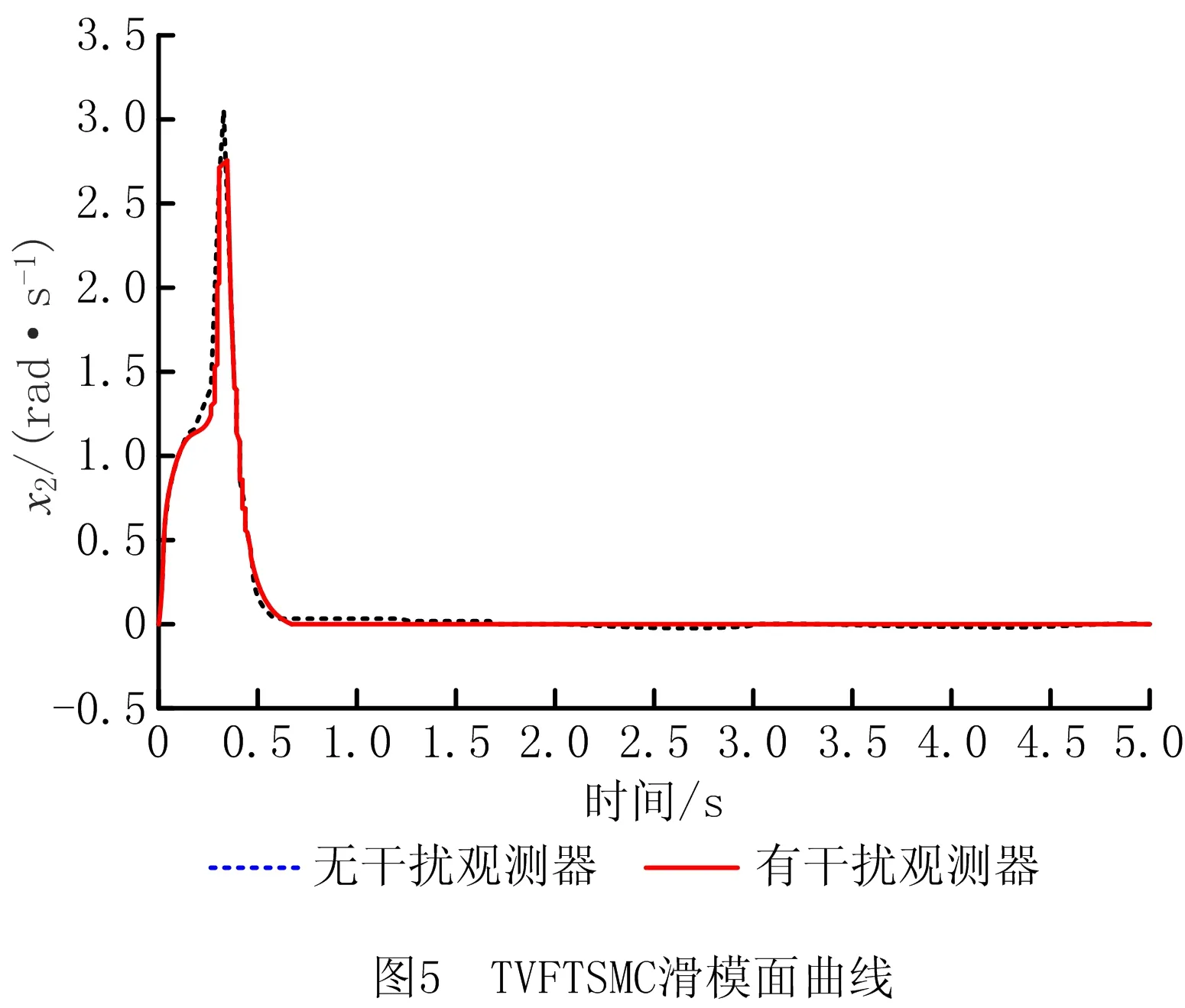
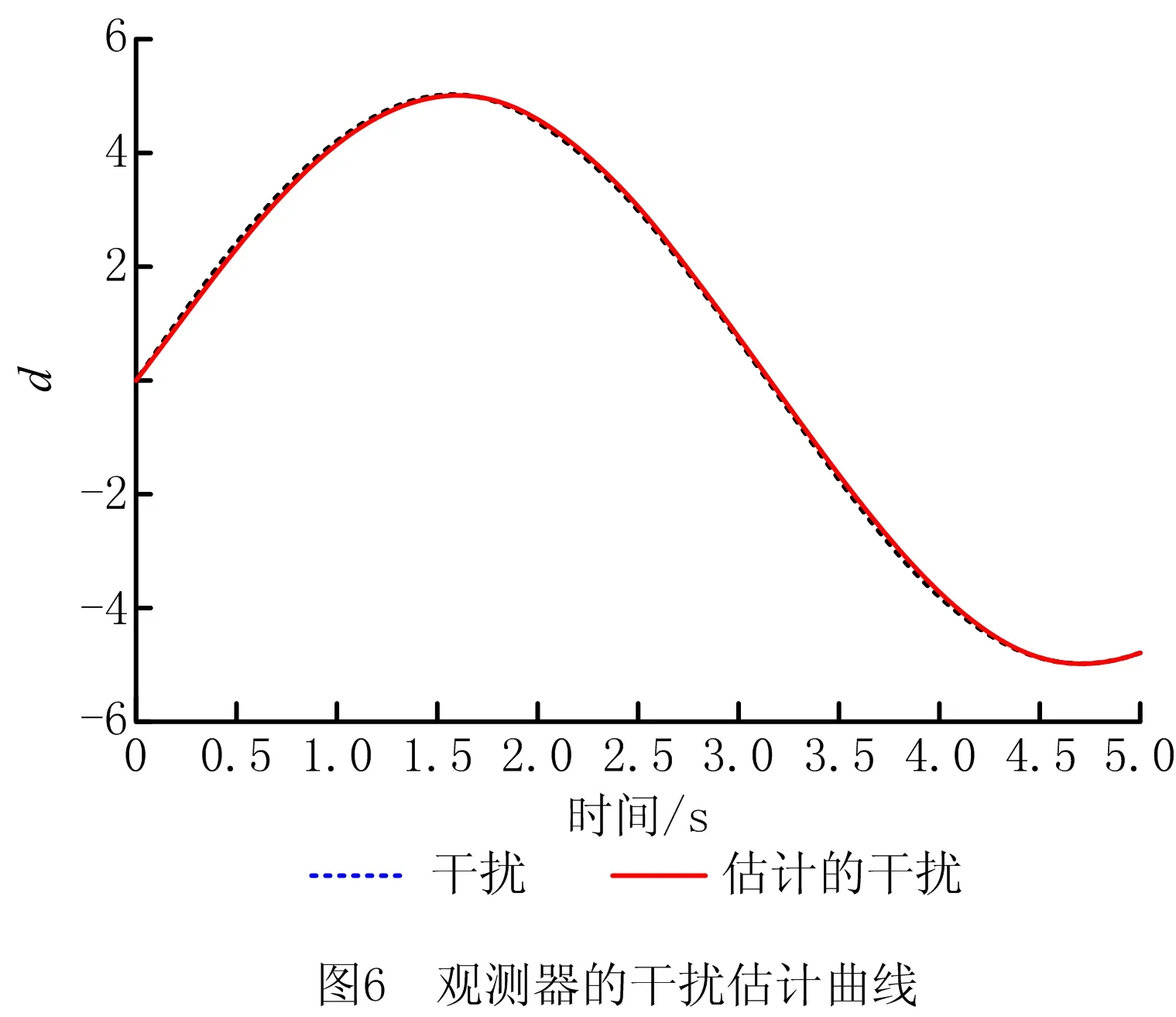
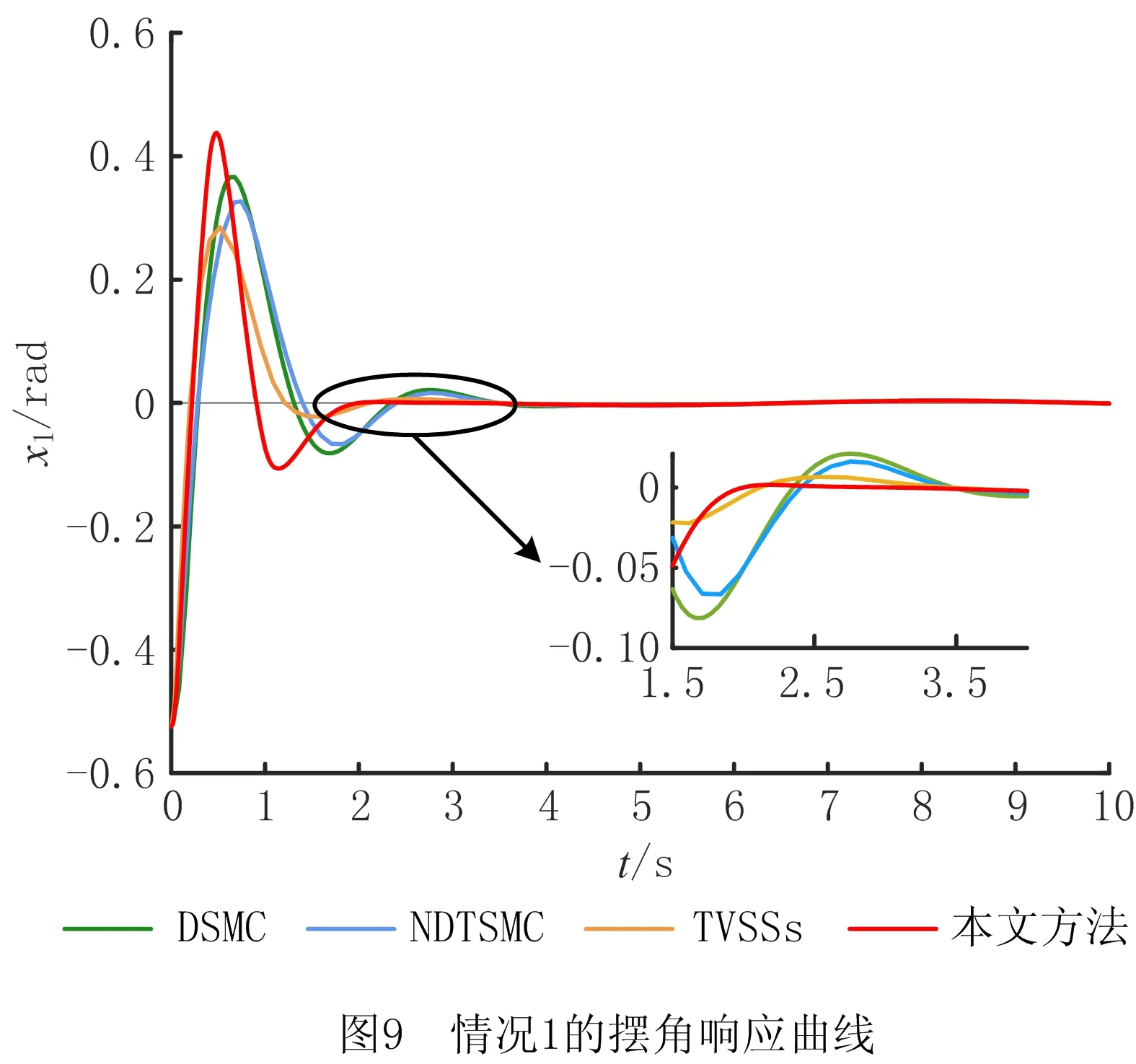
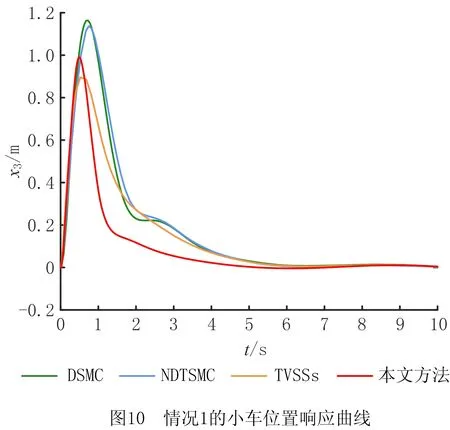
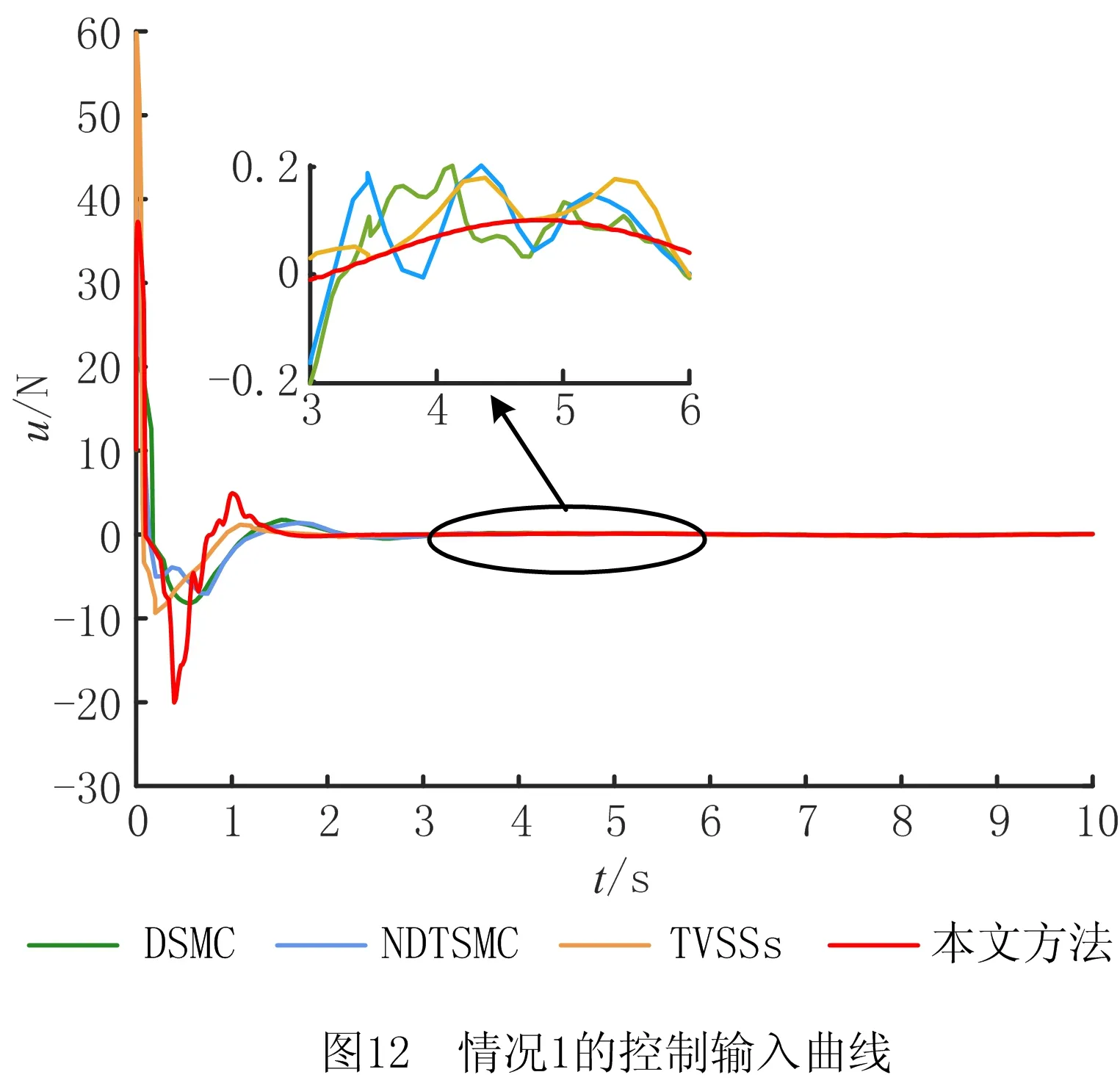
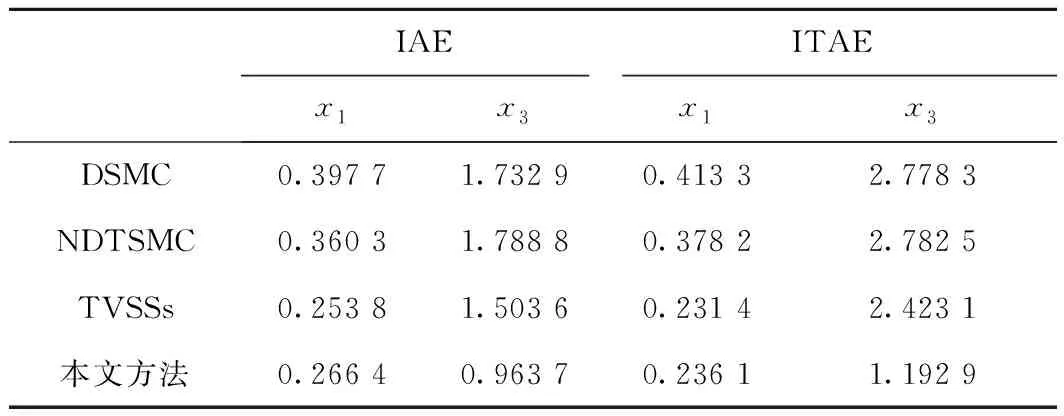
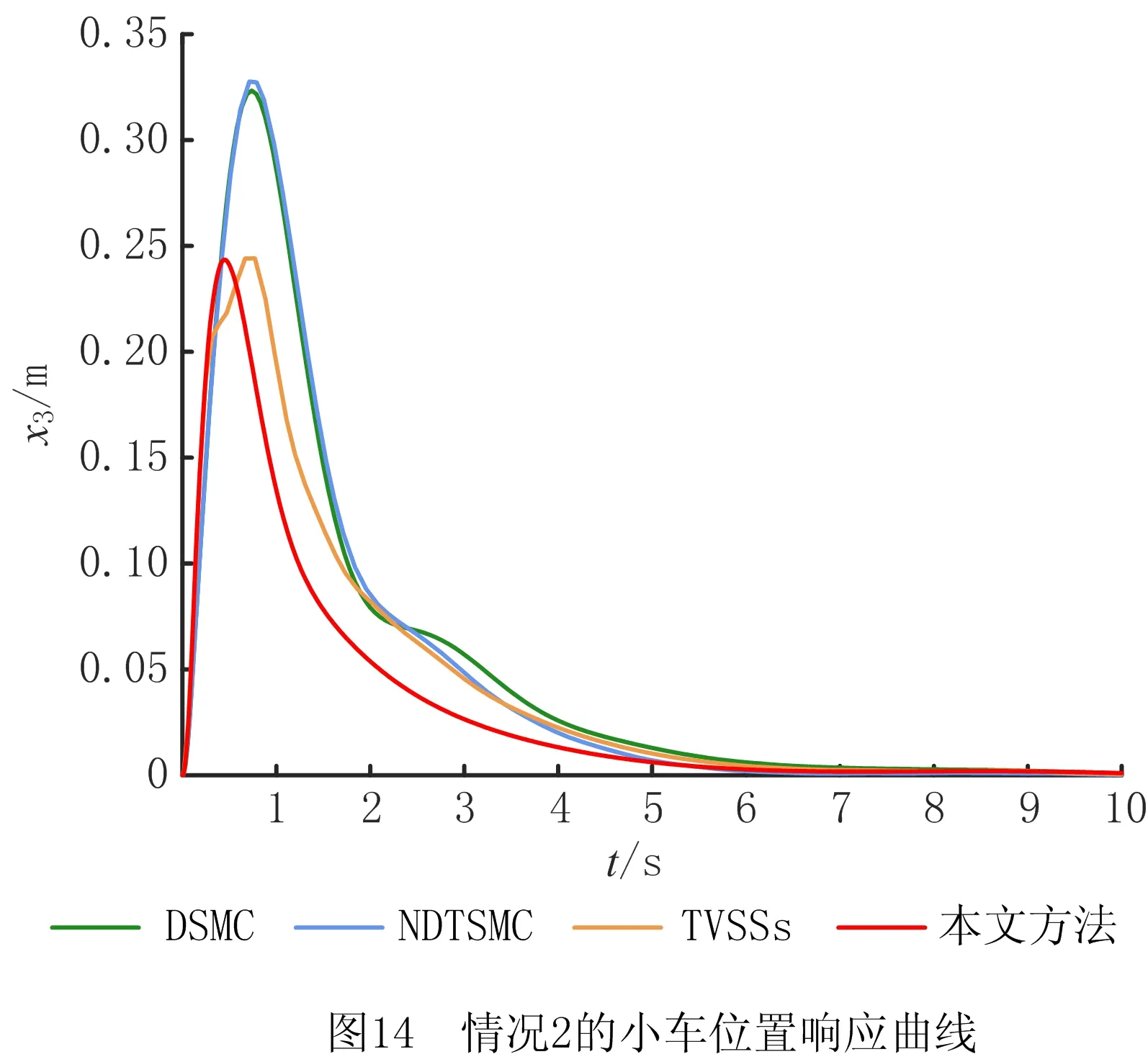
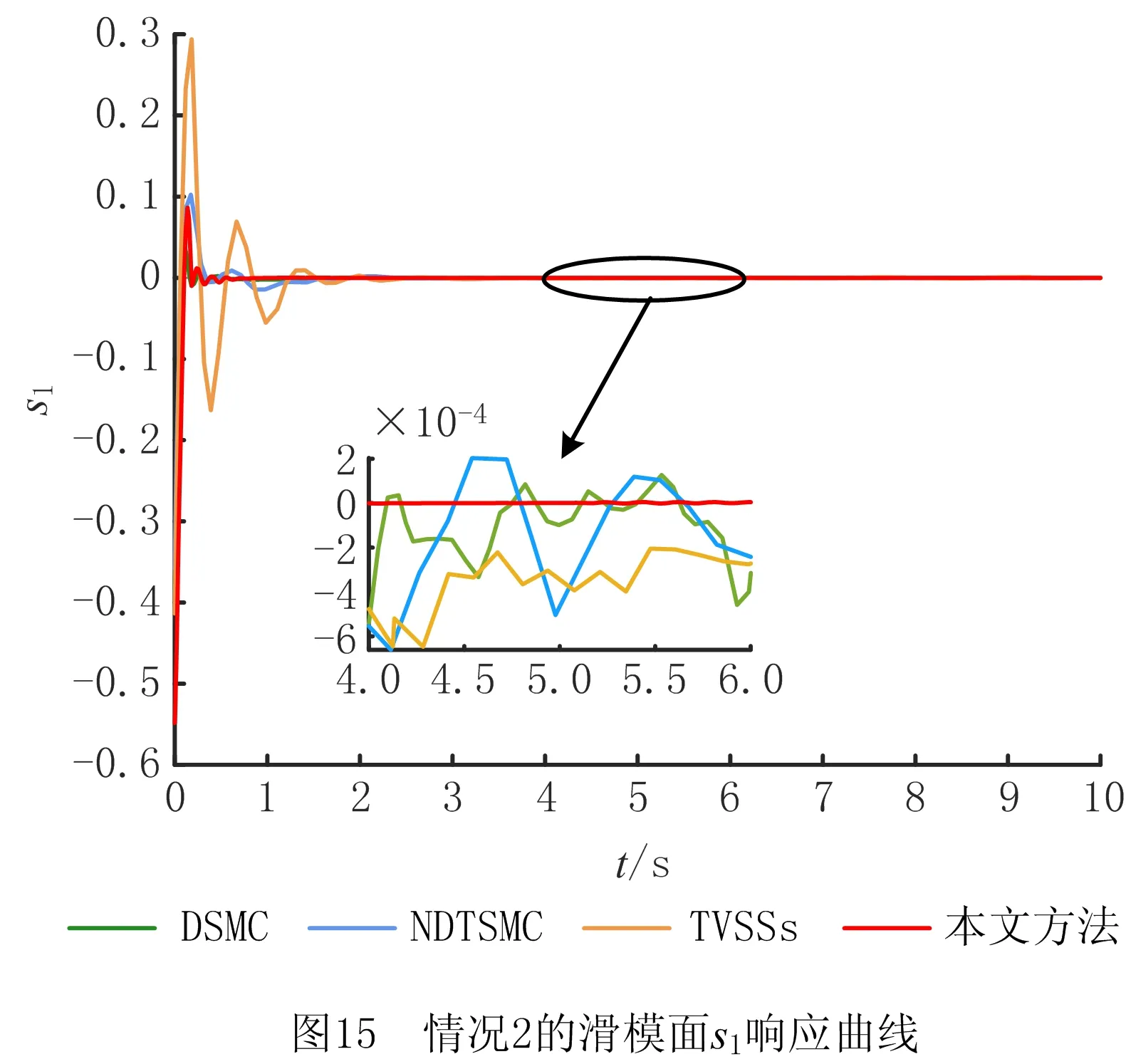
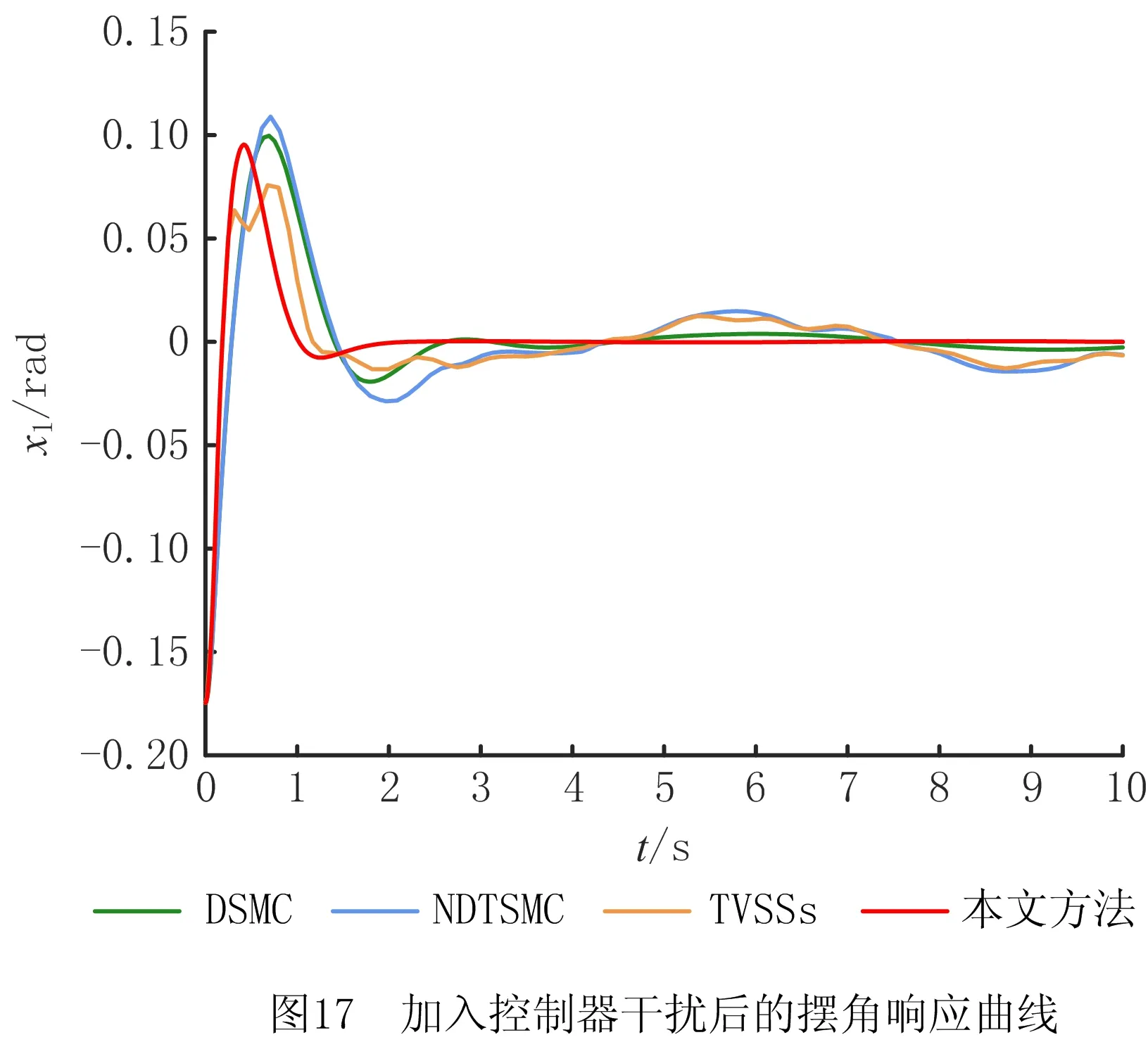
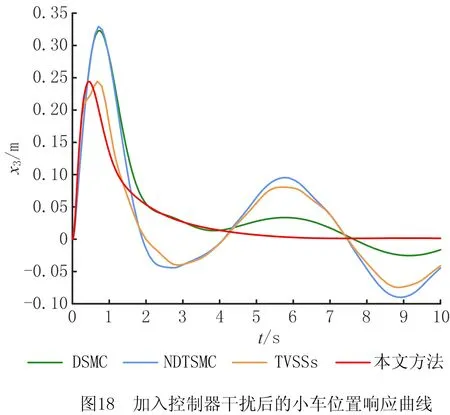
式中:α>0,λ>0;p和q是满足p (6) (7) 虽然由式(5)表示的FTSMC中,因增加了线性项αx1而提高了TSMC在状态远离平衡点时的收敛速度,但是在λ|x1|p/qsgn(x1)中,p和q的比值会影响系统状态的收敛速度,系统状态远离平衡点时希望比值大,系统状态趋近平衡点时希望比值小,无法使系统状态在整个滑模面快速收敛,而且比值太小会产生抖振。为此,本文根据文献[23]所提的FTSMC控制算法将滑模面改进为一种时变快速终端滑模(Time-Varying Fast Terminal Sliding Mode, TVFTSM),形式为 s=αx1+x2+λ|x1|γ(x1)sgn(x1)。 (8) 式中α和λ的取值与文献[22]相同。定义γ(x1)为关于状态x1的一个非线性函数, (9) (10) 定理1对于设计的时变快速终端滑模面(式(8)),系统状态在到达滑模面时可以在有限时间内收敛至平衡点,收敛时间为 (11) 证明构造Lyapunov函数 (12) 根据式(4)和式(8)对式(12)求导得 =x1(-αx1-λ|x1|γ(x1)) (13) 由式(13)可知,系统状态可以在有限时间内收敛。根据式(9)和式(10),γ(x1)关于状态x1变化,这里将状态x1分两种情况进行讨论: 根据式(10),式(8)可写为 s=αx1+x2+λ|x1|α1-β1sgn(x1)。 (14) 当系统状态到达滑模面s=0时,根据式(1)和式(14)可得 (15) 根据式(10),式(8)可写为 s=αx1+x2+λ|x1|α1+β1sgn(x1)。 (16) 当系统状态到达滑模面s=0时,根据式(1)和式(16)可得 (17) 综上所述,系统状态可以在有限时间内收敛,且在趋近阶段的收敛时间 T=t1+t2。 (18) 二阶非线性系统以小车倒立摆系统(式(4))为例进行仿真对比,如图1~图3所示。 FTSMC的控制参数设定基于文献[23],为了客观对比滑模面,所提TVFTSMC选择式(8),此时设置α1=1.5,β1=0.6,Δ=0.1,κ=30,其余控制参数与FTSMC相同。从图1~图3可见,无论摆角、摆角角速度还是滑模面,TVFTSMC的收敛速度均快于FTSMC。 考虑到TVFTSMC抑制干扰的能力不足,根据毛海杰等[24]和DONG等[25]提出的跟踪微分器,设计基于双曲正切跟踪微分器的非线性干扰观测器实时估计系统干扰,以削弱扰动对系统控制精度的影响。双曲正切跟踪微分器可以保证所提干扰观测器的稳定性和收敛性,且具有优秀的跟踪性能,可用于估计多种类型不确定扰动,并可克服现有干扰观测器需要扰动上下界及其第i个导数Lipschitz上界的先验信息的缺点。 以二阶非线性系统(式(4))为例,考虑系统 (19) 式中:x2和u分别为系统状态和控制输入,x2∈,u∈;d为系统的外部干扰,d∈。 引理1[26]对于系统 (20) 引理1提供了一种基于跟踪微分器干扰观测器的通用设计方法,可通过构造合适的跟踪微分器,进一步将其应用于干扰观测器设计。 双曲正切函数在平衡点附近近似为线性函数,在远离平衡点时具有非线性函数的特点[24],基于双曲正切函数设计的跟踪微分器形式简单,需要整定的参数较少,由于其函数光滑连续,可以有效抑制输出抖振。本文所提干扰观测器的突出优点是几乎可以估计所有类型的干扰,且不需要干扰的先验信息。基于双曲正切跟踪微分器设计的非线性干扰观测器如下: (21) 此时,考虑外部干扰d=5sin(t),二阶非线性系统以小车倒立摆系统(式(4))为例,所提TVFTSMC控制算法在有无非线性干扰观测器两种情况下的仿真对比如图4和图5所示。图6所示为观测器的干扰跟踪曲线,可见非线性干扰观测器可以很好地估计外部干扰,并将估计的干扰补偿给控制器,抑制了扰动对控制精度的影响,使系统状态可以在有限时间内收敛,从而削弱控制输入抖振,提高系统鲁棒性。 综上所述,所提TVFTSMC控制算法在非线性二阶系统中具有良好的控制性能,然而若直接应用于四阶欠驱动系统,则将因其强耦合性质而严重影响TVFTSMC的控制效果。为解决该问题,下面对本文所提方法结合解耦控制算法在四阶欠驱动系统中的控制性能进行讨论。 根据文献[27]提出的解耦滑模控制(Decoupled Sliding Mode Control, DSMC),将四阶非线性系统(式(3))分解为如下两个子系统分别设计滑模面: (22) (23) 每个子系统基于滑模面有单独的控制目标,目的是提出一种控制策略,使得两个子系统的状态从初始状态到达滑模面s1=0和s2=0,然后沿滑模面趋近至原点。 设计非线性系统(式(3))的时变快速终端滑模面s1和s2: (24) 式中:a1,λ1,a2,λ2>0;γ1(x1-z)和γ2(x3)为式(9)所示的非线性函数, γ1(x1-z)= α1+β1tanh[κ1((x1-z)2-Δ1)], (25) (26) z表示将子系统B的滑模面信息引入子系统A的滑模面中, z=zu×sat(s2/φ),0 (27) 式中:sat(s2/φ)为饱和函数, (28) φ为s2的边界层厚度且为正常数;zu为|z|的上界,且0 根据式(9)、式(22)和式(27),对滑模面s1求导: ×ln(|x1-z|)sgn(x1-z)+f01+b1u+n1; (29) (30) (31) 为保证到达滑模面,选取双幂次趋近律为[28] k2|s1|c2sgn(s1)。 (32) 式中:c1,c2,k1,k2为正常数,且0 根据式(29)、式(31)和式(32)可得控制器的切换控制项 usw=-[k1|s1|c1sgn(s1)+ k2|s1|c2sgn(s1)]/b1。 (33) 因此系统整体的控制律为u(t)=ueq+usw, (34) (35) (36) 定理2针对非线性系统(式(3)),用干扰观测器估计系统总扰动,选取滑模面(式(24)),在控制律(式(35))作用下,非线性系统(式(3))的整体滑模面可以在有限时间内收敛到区间 |s1|≤min{(δ/k1)1/c1,(δ/k2)1/c2} (37) 内,且收敛时间 (38) 证明定义Lyapunov标量函数 (39) 对V求一次时间导数并将式(3)、式(24)和式(34)代入,已知干扰观测器估计的干扰误差|ξ|≤δ,可得 =s1(-k1|s1|c1sgn(s1)-k2|s1|c2sgn(s1)+ξ) =-k1|s1|c1+1-k2|s1|c2+1+ξs1 ≤-k1|s1|c1+1-k2|s1|c2+1+δ|s1|。 (40) 设δ≤k1|s1|c1+k2|s1|c2,将式(40)化为如下两种形式: (41) (42) (1)|s1|≥(δ/k2)1/c2 (43) 因此,V由V0收敛至V1所需的时间T1≤T1max,其中V0和s0分别为Lyapunov函数V和滑模面s1的初始值,且 (44) (2)|s1|≥(δ/k1)1/c1 (45) 同理可知,V由V0收敛至V2所需的时间T2≤T2max,其中 (46) 综上所述,系统总体滑模面s1将在有限时间内收敛至如式(37)所示的区域,定理2得证。 定理3对于非线性系统(式(3)),选取滑模面(式(24)),在控制律(式(35))作用下,系统状态轨迹将在有限时间内收敛到平衡点。 证明设t1≤γ1(x1-z)≤t2,其中t1,t2为正常数,则滑模面s1可表示为: s1a1(x1-z)+x2+λ1|x1-z|t2sgn(x1-z); s1≥a1(x1-z)+x2+λ1|x1-z|t1sgn(x1-z)。 (47) (48) 进一步得出: (49) 式(49)的解可表示为: (50) 倒立摆系统是控制科学中典型的物理模型,常用于检验新的控制理论和算法的正确性及其在实际应用中的有效性,其控制方法在半导体及精密仪器加工、人工智能、机器人控制技术、导弹拦截控制系统、航空对接控制技术、火箭发射中的垂直度控制、卫星飞行中的姿态控制和一般工业应用等方面均具有广阔的前景。为了验证所提控制策略的有效性和优越性,采用MATLAB对小车倒立摆系统进行仿真,并分别与文献[19-20,29]提出的非奇异解耦终端滑模控制(Nonsingular Decoupled Terminal Sliding Mode Control, NDTSMC)、TVSSs、DSMC进行对比仿真。小车倒立摆系统模型如图8所示,其动态方程可用式(3)表示,其中系统的非线性函数f01(x),b1(x),f02(x),b2(x)分别为: f02(x)= (51) 式中:x1为摆杆与垂直轴的角度;x2为摆杆的角速度,x3为小车位置;x4为小车速度;mt为小车倒立摆系统的总质量(包括摆杆和小车的质量mp和mc,mt=mp+mc);L是摆杆长度的一半。为了仿真,设置小车倒立摆的系统参数和初始条件L=0.5 m,mc=1 kg,mp=0.1 kg,g=9.8 m/s2,x(0)=[-30°,0,0,0]T。 设小车倒立摆系统的参数不确定性Δf1(x)=0.5sin(x1),Δf2(x)=0.5sin(x3),系统外部干扰d1=d2=0.087 3sin(t),则n1=0.087 3sin(t)+0.5sin(x1),n2=0.087 3sin(t)+0.5sin(x3)。 表1所示为本文所提方法NDOTVDFTSMC和对比方法的控制参数。为了更加客观地与其他控制方法比较,本文对文献[19-20,29]的部分参数进行了少量改动。 表1 仿真中使用的控制参数 将本文所提NDOTVDFTSMC与DSMC,NDTSMC,TVSSs进行对比,其摆角、小车位置、控制输入量和滑模面s的响应曲线分别如图9~图12所示。 为了评估控制算法的稳定性和优越性,引入如下两个性能指标: (1)绝对误差积分准则(IAE) (52) (2)时间乘误差绝对值积分(ITAE) (53) 式中ei(τ)为系统状态与期望值之间的误差。 表2所示为各方法应用于小车倒立摆系统的IAE值和ITAE值。可见,对于系统小车位置状态x3的稳定性和收敛性,本文所提方法的IAE和ITAE值更小,系统稳定性更好;对于系统摆角状态x1,因为其他3种方法优先考虑的是状态x1的动态品质,所以系统状态x1的两项指标明显优于状态x3,而本文方法兼顾摆杆摆角和小车位置状态的动态品质,在状态x3的性能指标比其他方法有较大优势的基础上,系统状态x1的稳定性虽与TVSSs相比无明显差异,但明显优于其他方法。综合上述结果说明,与其他方法相比,所提方法具有更好的稳定性和动态品质。 表2 各种方法应用于小车倒立摆系统的IAE和ITAE值 图9和图10所示分别为系统摆角和小车位置的暂态响应曲线,虽然所提控制方法摆角的超调量较大,但是收敛速度明显快于其他控制方法;对小车位置而言,无论超调量还是收敛速度,所提控制方法均具显著优势,而且稳态误差更低。相比DSMC,所提控制算法能够保证系统状态在有限时间内收敛;相比NDTSMC,所提控制算法之所以能够快速收敛的一部分原因是加入了线性项,并将其在控制器对位移极点的作用过程中应用于系统;相比TVSSs,因为所设计的非线性函数构造的时变滑模面兼顾系统状态在各时刻的收敛速度,所以缩短了整个趋近过程中的收敛时间。 图11和图12所示分别为不同控制算法的系统整体滑模面曲线和控制输入曲线,可见所提控制方法的滑模面在更短时间内收敛且保持稳定。由于本文方法使用时变滑模面,滑模面函数中的指数项通过设计的非线性函数进行优化调整,从而保证系统状态在远离或接近滑模面时都具有较快的收敛速度,滑模面和控制器的部分参数在收敛稳定之前也随系统状态变化,目的是解决快速终端滑模指数项参数的取值限制问题,最大化快速终端滑模的趋近速率。因为系统状态的响应曲线对滑模函数指数项参数的变化比较敏感,所以所提控制方法在收敛前会出现一定抖振,然而无论滑模面曲线还是控制输入曲线,收敛至稳态后的抖振都更小。 为了进行鲁棒性分析,在不同的初始条件、参数不确定性和外部扰动下重复进行仿真研究。设系统初始条件x(0)=[-10°,0,0,0]T,参数不确定性Δf1(x)=0.6sin(x1),Δf2(x)=0.6sin(x3),系统外部干扰d1=d2=0.01sin(t)。 摆角位置、小车位置、滑模面和控制输入的响应曲线分别如图13~图16所示,与本文的研究结果相似,也证实了所提控制方案在不同条件下都具有良好的鲁棒性。 在此基础上,增加控制器干扰n=2sin(t),系统表示为: (54) 系统摆角和小车响应曲线如图17和图18所示,相比其他控制方法,加入控制器干扰后,本文方法的控制性能仍然具有优越性和系统稳定性,这归功于非线性干扰观测器对系统总体干扰的实时观测。 针对一类四阶欠驱动非线性系统,本文提出一种NDODTVFTSMC策略,旨在提高和优化现阶段提出的TSMC的趋近速率和抖振现象。所提控制策略结合传统滑模控制在状态远离平衡点时收敛快和终端滑模能在有限时间内收敛的优点,用一个非线性函数将快速终端滑模设计为时变快速终端滑模,从而提高系统在各阶段的收敛速度,再通过解耦算法完成了对四阶系统的稳定控制。仿真结果和数值分析表明,相比DMSC,NDTSMC,TVSSs,所提时变快速终端滑模提高了系统状态的收敛速度,削弱了抖振,并利用基于双曲正切跟踪微分器的非线性干扰观测器有效抑制外部扰动和系统不确定性,提高了系统控制的鲁棒性,使本文方法在抑制抖动、稳定性、响应速度等各方面均具明显优势。

2.2 基于双曲正切跟踪微分器的干扰观测器


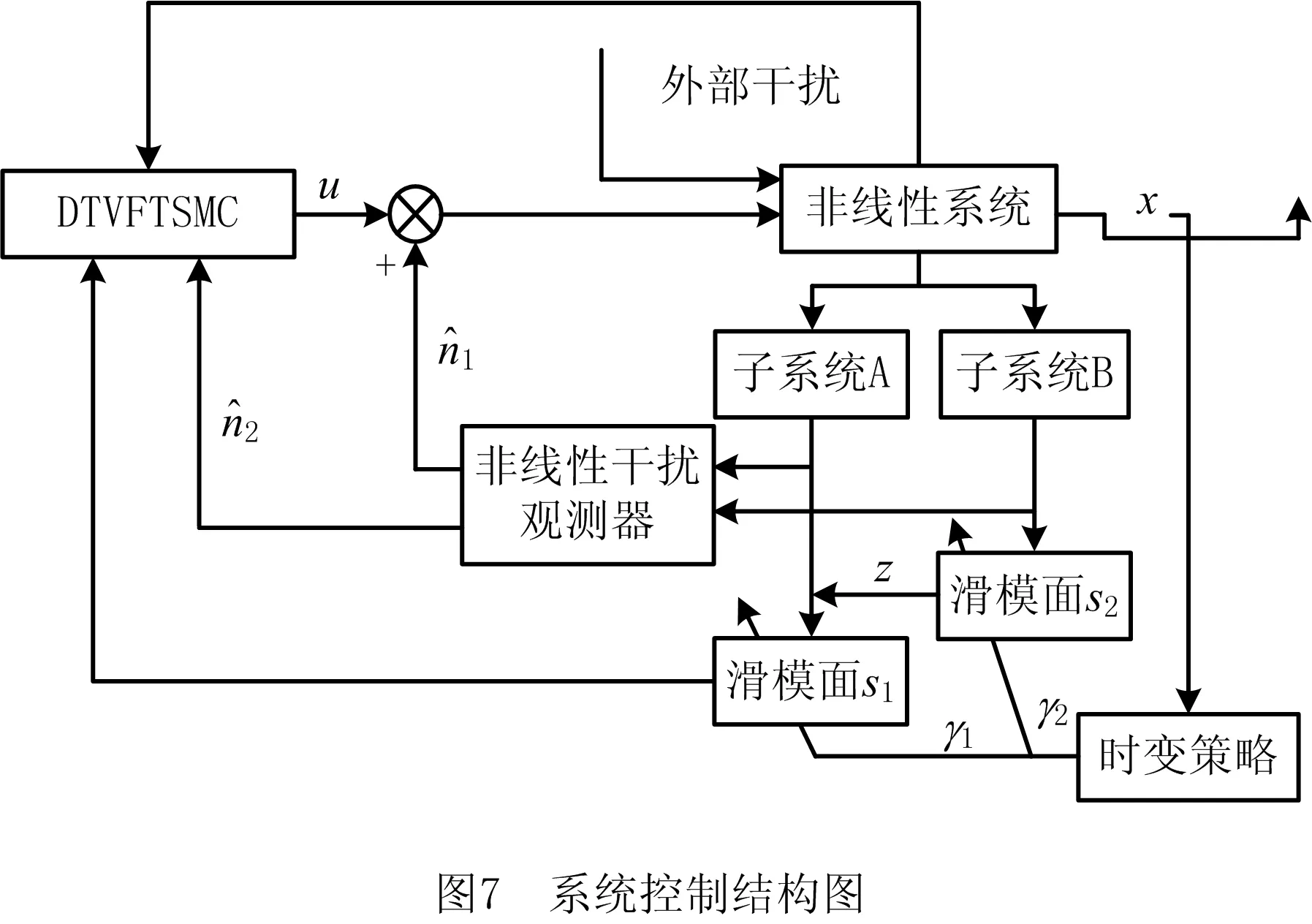
3 基于非线性干扰观测器的解耦时变快速终端滑模控制
3.1 基于干扰观测器的解耦时变快速终端滑模控制


3.2 稳定性分析
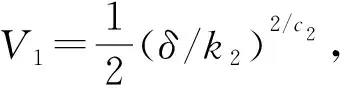
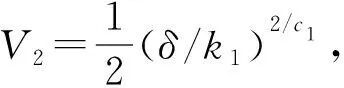

4 仿真分析






5 结束语

