一种用于电缆行波测距的解耦矩阵改进方法

王 植，王 宾，张慧芬

（1.济南大学自动化与电气工程学院，山东 济南 250022；2.电力系统及发电设备安全控制和仿真国家重点试验室（清华大学电机系），北京 100084）

0 引言

随着我国城市化进程的加快，城市规模不断扩大，电力需求呈高速增长的趋势[1-2]，电缆在城市电网中的覆盖率逐年提高[3]。电缆一般敷设于地下，如果发生故障，故障点难以查找，通过测距精准确定故障点位置，可提高供电可靠性。行波法是故障测距的一种主流方法，选用行波法进行测距，需对电缆进行解耦。

Clarke变换矩阵[4]和 Karenbauer变换矩阵等传统的解耦矩阵只考虑了线芯之间的电磁耦合，仅适用于架空线路。结构复杂的电缆不仅有线芯，还有金属护套和铠装层，只考虑线芯之间的电磁耦合会影响电缆的测距精度，甚至让测距失效。

扩展的Clarke变换矩阵将金属护套和铠装层视为一个整体，考虑了线芯与金属护套和铠装层之间的电磁耦合，但固定的Clarke变换矩阵不能随频率变化。本文分析传统扩展Clarke变换矩阵的不足，对其进行了改进，改进的Clarke变换矩阵随频率发生改变，在固定频带下可达到更好的测距效果，满足电缆的测距需要。

1 电缆的敷设方式及解耦需求

在实际的配电网中，电缆的敷设方式通常分为直埋敷设、排管敷设、电缆沟敷设和隧道敷设4种[5]。当电缆的敷设方式为直埋和排管时，各相电缆之间被土壤填充，可归为同一类进行分析。

直埋电缆的排列方式有品字排列、竖直排列、水平排列和直角排列4种[6]。在实际工程中，使用最多的排列方式为品字排列和水平排列。配网电缆的各相线芯、金属护套之间存在电磁耦合，其故障暂态分析复杂。传统的解耦矩阵只考虑了各相线芯之间的耦合关系，没有考虑其与金属护套之间的耦合关系，解耦不彻底。当应用于行波测距时，如果算法的灵敏性过高，可能误判行波的到达时刻，会进一步造成各模量波速计算不准确，影响测距结果。

2 传统Clarke变换存在的问题

三相单芯电缆6种传输模量具体为导体同护层之间的3个同轴模量即模量4、模量5和模量6，护层之间的2个护层模量即模量2和模量3，护层同大地之间的1个接地模量即模量1。传统Clarke扩展矩阵模量示意图如图1所示。

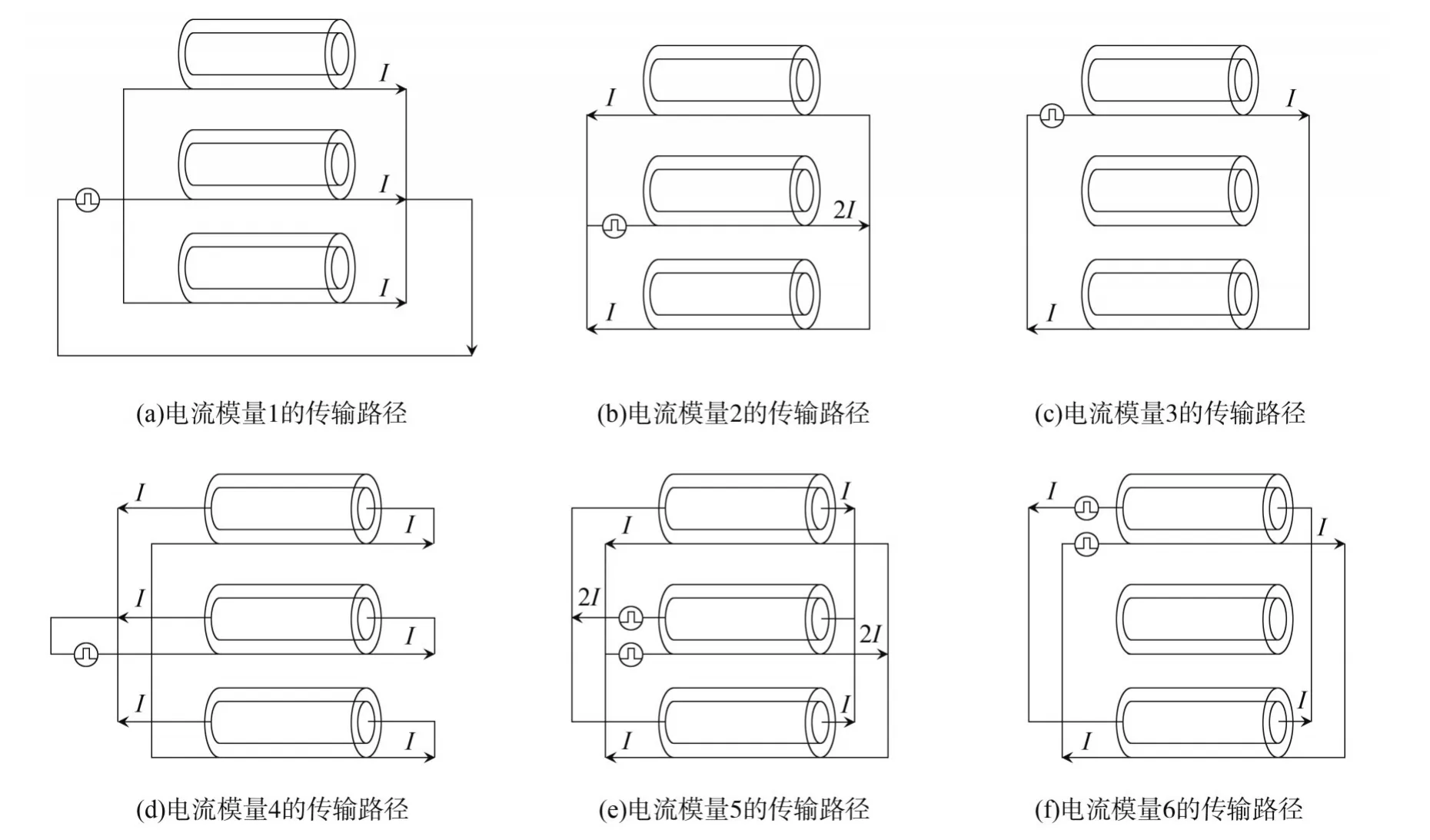
图1 传统Clarke扩展矩阵模量示意图

模量1：各相电流经过金属护层并从大地返回，类似于架空线路的零序模量，其传输速度最低且衰减系数最大。

模量2和模量3：对应于金属护套层-金属护套层回路，在一个金属护套层中流动的电流从其他相的一个或两个金属护套层中返回。

模量4：相同的电流注入各相的线芯，并从相应的金属护层中返回，具有零序模量的性质。

模量5：在中间相的线芯注入电流，从一边相的线芯中流出一半，从另一边相的线芯中流出另一半。

模量6：在边相的线芯中注入电流，从另一边相的线芯中返回，其模量的表现类似于模量5。

传统的Clarke扩展矩阵在计算中将线芯或者金属护套的自阻抗视为同一数值，未考虑埋藏深度对线芯或阻抗的影响，埋藏深度同时影响两相电缆的线芯之间的互阻抗，从而影响解耦效果。

3 Clarke解耦矩阵的改进

为了对电缆线路进行解耦，必须确定电缆多导体间的电磁耦合关系[7]。

电缆的典型结构如图2所示，包括线芯，内绝缘层，金属护套层，外绝缘层4层[8]。

图2 电缆的典型结构

本文分析的电缆敷设方式为品字排列的直埋电缆，每相电缆有两个导体，三相电缆共6个导体，相应的配电网三相电缆的阻抗矩阵Z、导纳矩阵Y为6阶方阵。

阻抗矩阵Z的第一行到第六行和第一列到第六列分别对应电缆A相、B相和C相的线芯及A相、B相和C相的金属护套层。阻抗矩阵Z中的元素Zmn代表不同类型的阻抗：三相中某一相的线芯自阻抗、三相中某一相的金属护套自阻抗、三相中其中两相之间的线芯互阻抗、三相中其中两相之间的金属护套互阻抗、三相中不同相金属护套与线芯之间的互阻抗。

同理，导纳矩阵Y中的元素Ymn代表不同类型的导纳：三相中某一相的线芯自导纳、三相中某一相的金属护套自导纳、三相中其中两相之间的线芯互导纳、三相中其中两相之间的金属护套互导纳、三相中不同相金属护套与线芯之间的互导纳。当频率达到5 kHz时，线芯和金属护套之间的互阻抗ZRD与金属护套的自阻抗ZDD相差较小，接近于相等，在运算过程中将二者作相等处理[9]。

本文将线芯的自阻抗视为不同数值，用ZRR和ZRR′加以区分；将金属护套的自阻抗视为不同数值，用ZDD和ZDD′加以区分；将两相电缆的线芯之间的互阻抗也视为不同数值，即Z1和Z2。

类比架空输电线路，列写电缆传输方程如下：

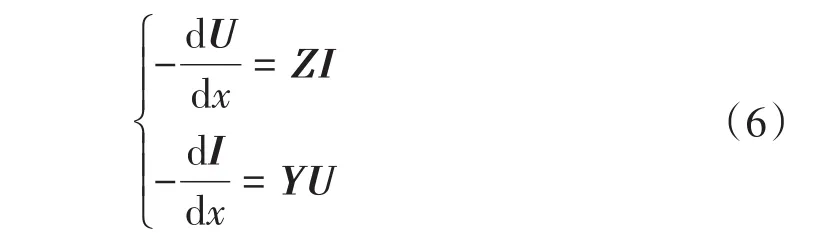
左右两边求微分，改写为二阶微分方程：

引入矩阵S和矩阵Q，经过S和Q的运算获得模量电压和模量电流[10]：

S和Q可将ZY矩阵和YZ矩阵对角化，即：

可见，电缆解耦的实质是寻找两个实矩阵S和Q使得ZY和YZ分别能够相似对角化。另外，如果取S=Q-T，则：

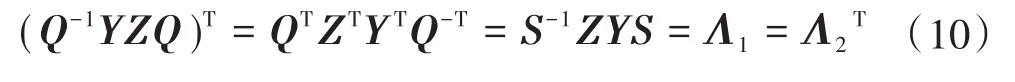
由此可知，当计算得到ZY矩阵的特征矩阵Q后，也可以得到矩阵S，其为Q的逆转置，ZY矩阵的形式如下：

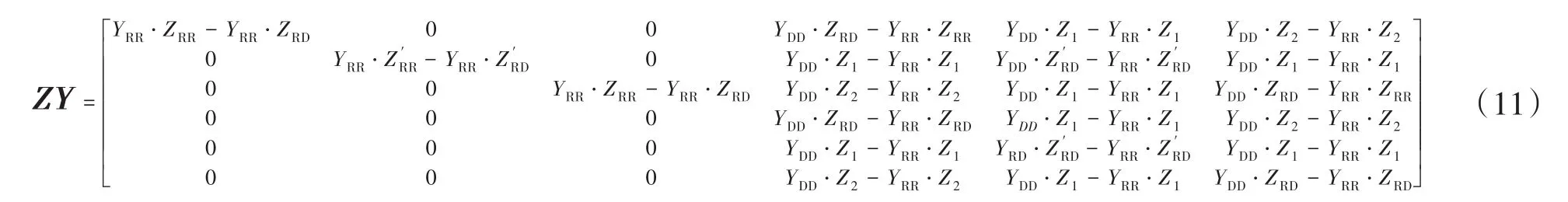
此时引进矩阵K：

式中，I为三阶单位矩阵，O为三阶零矩阵，利用矩阵K对矩阵ZY进行处理，得到如下形式：

用公式（13）将ZY矩阵转化为分块矩阵的形式：

对P1和P2分别对角化，即可对ZY矩阵对角化，观察P2矩阵可以发现，P2有如下形式：

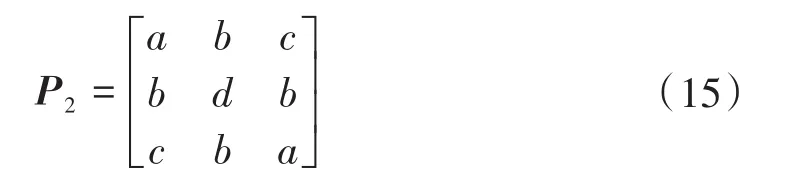
此时：

求得P2的特征值为：

P2的特征矩阵为：

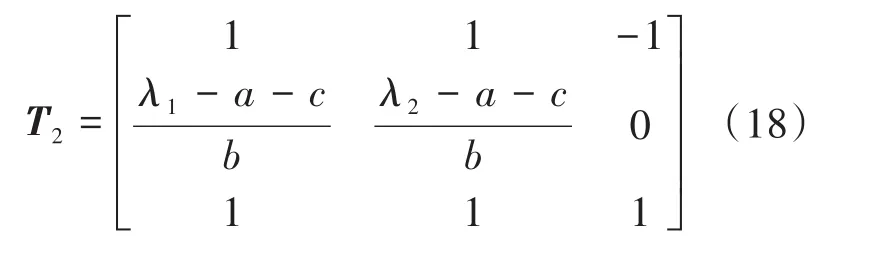
矩阵P1为对角阵，乘以任意的可逆矩阵都可以对角化。设P1的特征矩阵T1为-T2，则电压相模变换矩阵S为：

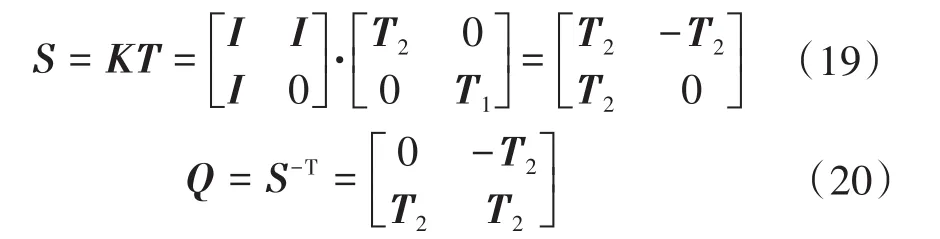
在计算过程中发现，Z和Y均为复数矩阵，所以通过计算得出的对角化矩阵Q和S也是复数矩阵，这给后续的计算和分析带来很多不便。矩阵Q和矩阵S虚数部分的值很小，将矩阵进行归一化后，略去较小的虚数，可以得到一个实数的解耦矩阵。实数解耦矩阵与复数解耦矩阵相比，对解耦产生的影响微乎其微，但可以大大简化计算，实数化的公式如下：

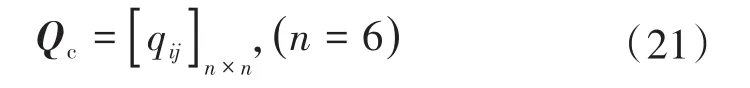
将ZY矩阵的复数形式的对角化矩阵记作：

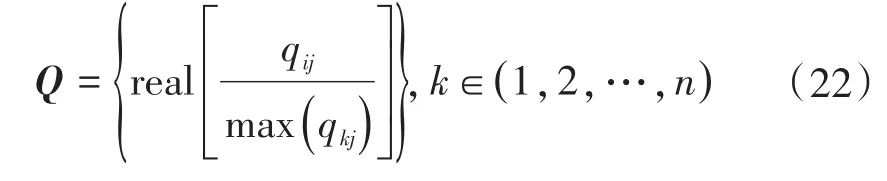
上式中real函数对复数矩阵取其实部，max函数取最大值完成归一化的目的，最后按照公式（20）计算出矩阵S，进而计算得到电压模量矩阵和电流模量矩阵。改进解耦矩阵模量示意图如图3所示。

图3 改进解耦矩阵模量示意图

可见模量3和模量6的表达式和传统的Clarke扩展矩阵并无区别，这是因为A相和C相的模量参数和传统的Clarke扩展矩阵相同，二者在同一埋藏深度。相比于传统的Clarke扩展矩阵，模量1和模量4的传输路径并没有发生改变，不过传输数值发生了改变，A相流过大地的电流为I，B相通过大地的电流略微减小，其减小的数值与A相流过大地的电流的比例为x。相比于传统的Clarke扩展矩阵，模量2和模量5的B相传输的电流分离了很小的一部分通过大地传输，使其具有了一定零模的性质。

4 仿真分析

本文利用PSCAD软件对电缆进行仿真分析，其敷设方式如图4所示。由图4可见，各相之间的距离均为0.5 m，A相和C相的埋藏深度相同，均为1.433 m，B相的埋藏深度为1 m。电缆的原始参数如表1所示。

图4 电缆的敷设方式

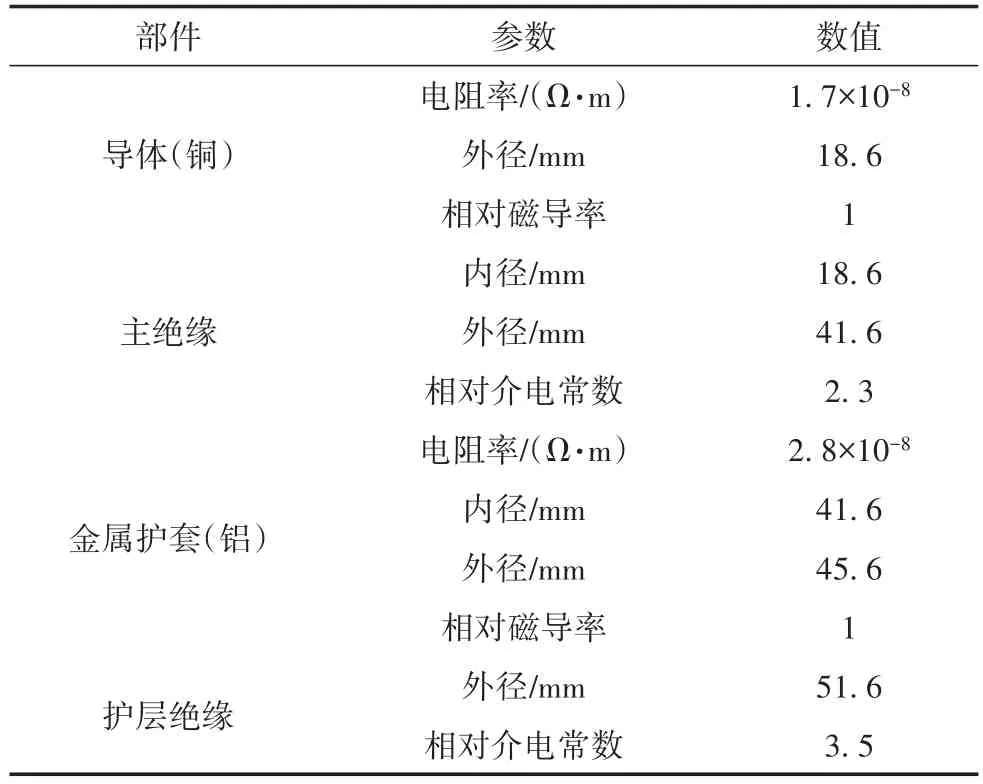
表1 电缆的原始参数

在170 kHz时电缆解耦之前的阻抗矩阵为：

假如按照传统的Clarke扩展矩阵进行解耦，则 得到的解耦后的矩阵为：

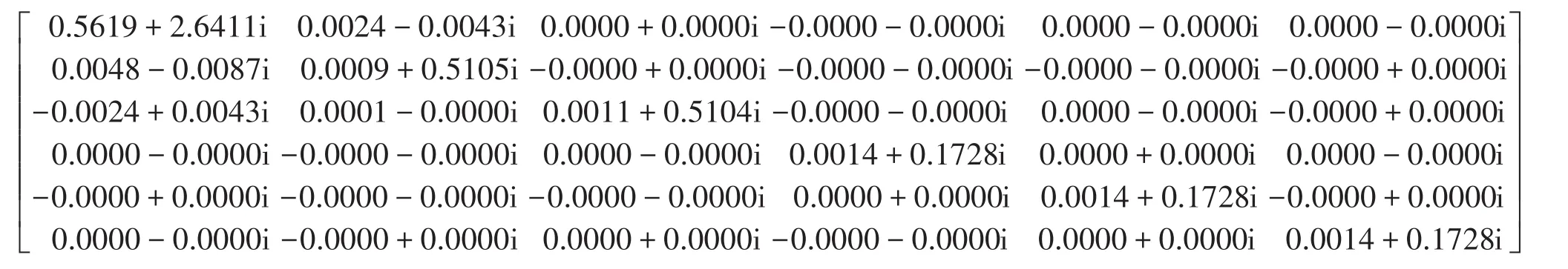
经过复数解耦矩阵运算得到的结果为：

可见，第一行第二个元素、第二行第一个元素、第三行第一个元素、第三行第二个元素都明显减小，说明改进的解耦方法对阻抗矩阵的解耦效果更好。解耦矩阵实数化后得到的矩阵为：

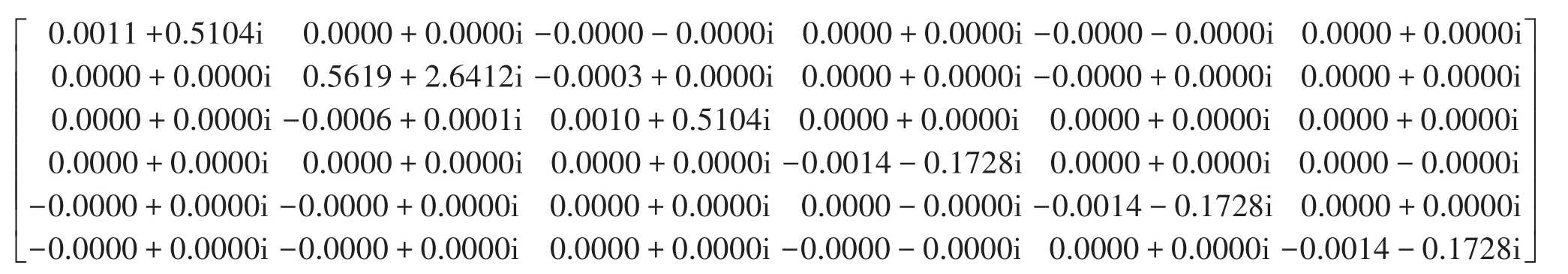
可见，将解耦矩阵实数化后对解耦效果产生的影响很小，可以忽略不计。

5 结语

本文对配电网电缆解耦方法进行研究，考虑埋藏深度的影响，将线芯或者金属护套的自阻抗及两相电缆的线芯之间的互阻抗视为不同值，根据电缆在不同频率下的参数设计不同的解耦矩阵，可以实现10-4量级的解耦，解决了传统解耦矩阵在电缆解耦方面解耦不彻底的问题。