闭模糊拟阵导出独立集的等价描述
吴 德 垠
(重庆大学 数学与统计学院, 重庆 401331)
基于拟阵的基本概念可得拟阵的许多等价描述(称为公理), 这些等价描述在拟阵理论中具有重要作用. 由于模糊拟阵[1]的复杂性, 目前关于模糊拟阵等价描述的研究文献报道较少. 文献[2-3]分别通过普通拟阵的基和圈, 给出了闭模糊拟阵的充要条件. 基于此, 本文通过普通拟阵的独立集, 讨论闭模糊拟阵的充要条件, 提出一种新的构造方法, 通过确定导出拟阵序列中全部拟阵的独立集族唯一确定一个闭模糊拟阵. 同时, 给出该方法的一个应用实例.
1 预备知识
设E={x1,x2,…,xm}是非空有限集,E上的模糊集全体记为[0,1]E,E的全体子集族(即幂集)记为2E.本文涉及的模糊数学相关概念和符号参见文献[1], 相关拟阵理论参见文献[4], 文献[4]通过独立集公理定义了拟阵.
定义1[1]设E是一个非空有限集,l⊆[0,1]E是一个满足下列条件的非空模糊集族:
1)(继承性) 若μ∈l,ν∈[0,1]E,ν≤μ, 则ν∈l;
2)(交换性) 若μ,ν∈l, |suppμ|<|suppν|, 则存在ω∈l, 使得
μ<ω≤μ∨ν,m(ω)≥min{m(μ),m(ν)}.
则称偶对M=(E,l)是E上的模糊拟阵,l称为M的独立模糊集族.∀μ∈[0,1]E, 若μ∈l, 则μ称为M模糊独立集.
该模糊拟阵也称为G-V模糊拟阵[5].文献[1]给出了将模糊拟阵分解为普通拟阵的如下方法.
定理1(模糊拟阵的分解定理)[1]设M=(E,l)是模糊拟阵, ∀r∈(0,1], 令Ir={Cr(μ)|∀μ∈l}, 则Mr=(E,Ir)是E上的拟阵(称为M的r-导出拟阵).存在有限实数列r0 1)r0=0,rn≤1; 2) 当0 3) ∀s,t∈(ri,ri+1),Is=It(0≤i≤n-1); 4) 若ri 对应定理1, 文献[1]中定理2.3部分解决了定理1的逆问题.文献[6]中定理2.8推广了文献[1]中定理2.3, 完全解决了闭模糊拟阵中定理1的逆问题. 定理2(闭模糊拟阵的合成定理)[6]设Mi=(E,Ii)(i=1,2,…,m)是E上的拟阵序列, 使得I1⊇I2⊇…⊇Im.取0=δ0<δ1<δ2<…<δm≤1, 令 l*={μ∈[0,1]E|∀r∈(0,1], 均有Cr(μ)∈Ir}, 其中∀r∈(0,1], 当r∈(δi-1,δi]时,Ir=Ii(i=1,2,…,m), 当δm<1,r∈(δm,1]时,Ir={Ø}.则: 1)M=(E,l*)是一个闭模糊拟阵; 2) 保留I1⊇I2⊇…⊇Im中每个等式段的最后一项, 去掉其余部分, 有Mi1=(E,Ii1)⊃Mi2=(E,Ii2)⊃…⊃Mih=(E,Iih), 于是组成了M的导出拟阵序列.通过下标对应知, 0=δ0<δi1<δi2<…<δih≤1为其基本序列. 综合定理1和定理2可知, 闭模糊拟阵由基本序列和导出拟阵序列唯一确定.即有: 推论1设M1=(E,l1)和M2=(E,l2)都是闭模糊拟阵.M1的基本列和导出拟阵序列分别为 M2的基本列和导出拟阵序列分别为 文献[7]给出了准模糊图拟阵的一个充要条件. 定理3[7]设M=(E,l)是一个闭模糊拟阵, 其基本序列和导出拟阵序列分别为 则M是准模糊图拟阵的充要条件是存在子集套[8]A1=E⊃A2⊃…⊃An, 使得Iri=Ir1|Ai(i=1,2,…,n), 其中Ir1|Ai表示独立集族Ir1在子集Ai上的约束[4]. 准模糊图拟阵有很多充要条件, 文献[9]给出了一个较典型的充要条件.本文将给出一个新的充要条件. 定理1中定义了模糊拟阵的导出拟阵.下面定义并讨论模糊拟阵的导出独立集和导出独立集映射. 利用定义2和定理1可证如下命题. 命题1设M=(E,l)是模糊拟阵, I为M的导出独立集族, 则下列结论成立: 1) I ={Cr(μ)|∀r∈(0,1], ∀μ∈l}; 下面讨论导出独立集的一个重要性质, 该性质是定义导出独立集映射的基础. 定理4设M=(E,l)是模糊拟阵, I为M的导出独立集族.则∀X∈I, 且X≠Ø, 存在正整数i, 使得∀r∈(0,ri), 均有X∈Ir; ∀r∈(ri,1], 均有X∉Ir. 证明: ∀X∈I, 根据I的定义, 存在μ∈l,λ∈(0,1], 使得X=Cλ(μ)∈Iλ, 即X∈Iλ.易见对任意s,t∈(0,1](s 定义3设M=(E,l)是模糊拟阵, I为M的导出独立集族.定义I上的映射ψ: I →{r1,r2,…,rn,1}.∀X∈I, 如果X≠Ø, 则根据定理4, 存在i(i=1,2,…,n)使得∀r∈(0,ri), 均有X∈Ir; ∀r∈(ri,1], 均有X∉Ir.此时, 定义ψ(X)=ri.如果X=Ø, 定义ψ(X)=1.ψ称为M的导出拟阵独立集映射, 简称导出独立集映射. 下面讨论导出独立集族和导出独立集映射的性质及关系. 定理5设M=(E,l)是模糊拟阵, I为其导出拟阵独立集族,ψ为其导出独立集映射, 则: 1) ∀X∈I, 当X=Ø时,ψ(X)=1; 当X≠Ø时,r1≤ψ(X)≤rn; 2) ∀Y∈I及∀X∈2E且X⊆Y, 有X∈I; 3) ∀X,Y∈I,X⊆Y, 有ψ(X)≥ψ(Y); 4)ψ是满射, 即∀r∈{r1,r2,…,rn,1}, 均存在X∈I, 使得r=ψ(X); 5) 若M是闭模糊拟阵, 则∀r∈{r1,r2,…,rn,1}, 均有Ir={X∈I|r≤ψ(X)}; 6) 若M是闭模糊拟阵, 则∀ri∈{r1,r2,…,rn}, 当ri 7) 若M是闭模糊拟阵, 取X,Y∈I, |X|<|Y|.如果存在r∈{r1,r2,…,rn}, 使得ψ(X)≥r,ψ(Y)≥r, 则存在Z∈I, 使得X⊂Z⊆X∪Y, 且ψ(Z)≥r. 证明: 1) 根据定理1和定理4可得结论. 2) 由命题1可知结论成立. 3) 由拟阵的继承性和定理4易知结论成立. ① 首先讨论r=1的情形.如果rn<1, 则I1={Ø}.又ψ(Ø)=1, 且∀X∈I,X≠Ø, 于是由1)知,r1≤ψ(X)≤rn<1.因此 Ir=I1={X∈I|r≤ψ(X)}={Ø}. 当rn=1时, 有{X∈I|r≤ψ(X)}={X∈I|rn=ψ(X)}.令I′={X∈I|r≤ψ(X)}.∀X∈I′, 均有ψ(X)=rn, 因此X∈Irn.即I′⊆Irn. 反之, ∀X∈Irn, 由定理4知, 有ψ(X)=rn.所以X∈I′, 即I′⊇Irn.综上可知I′=Irn. ② 其次讨论r=ri(i=1,2,…,n)的情形.令I′={X∈I|ri≤ψ(X)}.此时, I′={X∈I|ri=ψ(X)}∪…∪{X∈I|rn=ψ(X)}∪{X∈I|1=ψ(X)}. ∀X∈Iri, 由定理4知,ψ(X)≥ri, 因此X∈I′.即I′⊇Iri.∀X∈I′, 存在rj≥ri, 使得ψ(X)=rj, 于是ri∈(0,rj].根据定理4知,X∈Iri.因此I′⊆Iri.综上可知I′=Iri. 6) 当ri IriIri+1={X∈I|ri≤ψ(X)}{X∈I|ri+1≤ψ(X)}. 所以根据ri 当ri=rn时, ∀Y∈Irn, 由定理4知ψ(Y)≥rn.当rn=1时, 显然ψ(Y)=1=rn, 因此{X∈I|rn=ψ(X)}=Irn.当rn<1时,ψ(Y)=1⟺Y=Ø.所以当Y≠Ø时, 有ψ(Y)=rn.因此{X∈I|rn=ψ(X)}=Irn{Ø}. 7) 根据文献[4]中增广定理和定理4即可得结论成立.证毕. 设E={x1,x2,…,xm}是非空有限集合, 任取E上的一个子集族L⊆2E, 数列A={α1,α2,…,αk}(0<α1<α2<…<αk≤1), 满射ϑ: L→A∪{1}.∀r∈(0,1], 令Lr={X∈L|ϑ(X)≥r}. 定理6如果L,A和ϑ满足下列条件: (i)(规范性) ∀X∈L, 当X=Ø时, ϑ(X)=1; 当X≠Ø时,α1≤ϑ(X)≤αk; (ii)(继承性) ∀Y∈L及∀X∈2E且X⊆Y, 均有X∈L; (iii)(弱单调减) ∀X,Y∈L且X⊆Y, 均有ϑ(X)≥ϑ(Y); (iv)(增长性) ∀X,Y∈L, |X|<|Y|, 如果存在αi∈A, 使得ϑ(X)≥αi, ϑ(Y)≥αi, 则存在Z∈L, 使得X⊂Z⊆X∪Y, 且ϑ(Z)≥αi. 则通过L,A和ϑ可确定E上的一个闭模糊拟阵M*(L,ϑ). 证明: 1) ∀α∈A, 首先证明Mα=(E,Lα)均为拟阵. ① 由条件(i)及ϑ(Ø)=1知, ∀α∈A, 总有α≤1.因此ϑ(Ø)≥α, 于是Ø∈Lα.即Lα≠Ø. ② ∀Y∈Lα及∀X∈2E且X⊆Y, 证明X∈Lα.由条件(ii)知X∈L, 由Y∈Lα可得ϑ(Y)≥α.再由条件(iii)知,X∈L且ϑ(X)≥ϑ(Y)≥α.所以X∈Lα. ③ ∀X,Y∈Lα, |X|<|Y|, 证明存在Z∈Lα, 使得X⊂Z⊆X∪Y.由ϑ(X)≥α, ϑ(Y)≥α, 并利用条件(iv)知, 存在Z∈L, 使得X⊂Z⊆X∪Y且ϑ(Z)≥α, 于是Z∈Lα. 故根据文献[1]中定义1.1知,Mα=(E,Lα)是E上的一个拟阵. 2) 其次证明∀αi,αj∈A(i ∀X∈Lαj, 均有ϑ(X)≥αj.由i 3) 由1),2)可得拟阵序列Mα1⊇Mα2⊇…⊇Mαk.由ϑ是满射知, 存在X∈L(X≠Ø), 使得ϑ(X)=αk.于是X∈Lαk(⊃{Ø}), 即Lαk≠Ø.令α0=0, 构造E上的模糊集族: l*={μ∈[0,1]E|∀α∈(0,1], 均有Cα(μ)∈Iα}, (1) 其中∀α∈(0,1], 当α∈(αi-1,αi]时,Ia=Lai(i=1,2,…,k); 当αk<1,r∈(αk,1]时,Ir={Ø}. 由定理2知,M=(E,l*)是闭模糊拟阵.取M*(L,ϑ)=M=(E,l*), 即可知结论成立.证毕. 由于Lα1⊇Lα2⊇…⊇Lαk中可能出现等式, 因此M*(L,ϑ)的导出拟阵序列(相应的基本序列)是由该等式的最后一项产生.如果将条件加强, 则不会出现等式, 问题得到简化. (iii)*(强单调减) ∀X,Y∈L且X⊆Y, 均有ϑ(X)≥ϑ(Y).同时, ∀αi,αj∈α,i 定理7如果定理6中的L,A和ϑ满足条件(i),(ii),(iii)*和(iv), 则L,A和ϑ可唯一确定E上的闭模糊拟阵M*(L,ϑ)=(E,l*)(其中l*由式(1)定义), 且下列结论成立: 1)M*(L,ϑ)的基本序列为A={α1,α2,…,αk}(0=α0<α1<α2<…<αk≤1); 2)M*(L,ϑ)的导出拟阵序列为(E,Lα1)⊃(E,Lα2)⊃…⊃(E,Lαk); 3)M*(L,ϑ)的导出独立集族为L; 4)M*(L,ϑ)的导出独立集映射为ϑ. 证明: 由于条件(iii)*比条件(iii)更强, 因此, 由定理6可知L,A和ϑ可确定一个闭模糊拟阵M*(L,ϑ). 1),2) 证明∀αi,αj∈A(i 由定理6证明中2)知,Lαi⊇Lαj.再由条件(iii)*知|Lαi|>|Lαj|, 因此Lαi⊃Lαj.从而Lα1⊃Lα2⊃…⊃Lαk.由定理2知,M*(L,ϑ)的基本序列和导出拟阵序列分别为 3) 证明M*的导出独立集族是L.由命题1, 即证Lα1=L. 由Lα1的定义, 显然有Lα1⊆L.另一方面, ∀X∈L, 均存在αi∈A, 使得ϑ(X)=αi.由0<α1<α2<…<αk≤1知, ϑ(X)=αi≥α1, 所以X∈Lα1, 即Lα1⊇L.从而Lα1=L. 4) 证明M*(L,ϑ)的导出独立集映射是ϑ. 不妨设M*(L,ϑ)的导出独立集映射为ψ: L→A.∀X∈L, 均存在αi∈A, 使得ψ(X)=αi.若X=Ø, 则由条件(i)知, ϑ(X)=1.再由定义3知,ψ(X)=1.因此ψ(Ø)=ϑ(Ø).若X≠Ø, 则根据定理4知, ∀r∈(0,αi], 均有X∈Ir(Mr=(E,Ir)为M*(L,ϑ)的r-导出拟阵); ∀r∈(αi,1], 均有X∉Ir.因此X∈Lαi=Iαi, 但X∉Lαi+1=Iαi+1.根据Lα的定义知, ϑ(X)≥αi, ϑ(X)<αi+1, 于是ϑ(X)=αi=ψ(X).综上可得ϑ=ψ. 由推论1知, 通过基本序列和导出拟阵序列确定的闭模糊拟阵是唯一的.证毕. 下面给出本文的主要结果. 定理8(闭模糊拟阵的导出独立集公理) 设E={x1,x2,…,xm}是非空有限集合, 任取E上的一个子集族L, 数列A={α1,α2,…,αk}(0<α1<α2<…<αk≤1), 满射ϑ: L→A∪{1}.则L,A和ϑ分别是某个闭模糊拟阵的导出独立集族、 基本序列和导出独立集映射的充要条件是L,A和ϑ满足条件(i),(ii),(iii)*和(iv). 证明: ∀α∈(0,1], 仍令Lα={X∈L|ϑ(X)≥α}. 1) 必要性.设M=(E,l)是闭模糊拟阵, I为其导出拟阵独立集族,ψ为其导出独立集映射.此时, A={r1,r2,…,rn}, L=I, ϑ=ψ,Lri=Iri. 条件(i)即为定理5中结论1).根据命题1知, I=Ir1, 因此条件(ii)成立.条件(iii)*的前半部分即为定理5中结论2).由导出拟阵序列性质知条件(iii)*的后半部分也成立.因此条件(iii)*成立. ∀X,Y∈L, |X|<|Y|, 如果存在ri∈A, 使得ϑ(X)≥ri, ϑ(Y)≥ri, 则X,Y∈Lri=Iri.因此, 由文献[4]中增广定理知, 存在Z∈Lri, 使得X⊂Z⊆X∪Y.由于Z∈Lri, 所以ψ(Z)≥ri.于是条件(iv)也成立. 2) 充分性.此时, L,A和ϑ满足条件(i),(ii),(iii)*和(iv).由定理6知, Mα1=(E,Lα1)⊃Mα2=(E,Lα2)⊃…⊃Mαk=(E,Lαk) 是拟阵列, 结合数列0<α1<α2<…<αk≤1, 由式(1)可唯一确定一个闭模糊拟阵M*(L,ϑ)=M(E,l*).根据定理7中结论3),4)知, 闭模糊拟阵M*(L,ϑ)的导出独立集族、 基本序列和导出独立集映射分别是L,A和ϑ.证毕. 下面利用定理8讨论准模糊图拟阵的一个充要条件.首先, 根据定理3、 命题1和定理5中结论5)可得准模糊拟阵的一个如下性质. 命题2设M=(E,l)是一个准模糊图拟阵, 其基本序列和导出拟阵序列分别为 令A={r1,r2,…,rn}.再设I和ψ分别是M的导出独立集族和导出独立集映射.∀α∈(0,1], 令Lα={X∈I|ψ(X)≥α}.则存在子集套A1=E⊃A2⊃…⊃An, 使得∀ri∈A, 均有Lri=I|Ai=Iri. 根据命题2, 在导出独立集族上可定义一个加强单调减性质为: (iii)**(加强单调减) ∀X,Y∈I且X⊆Y, 均有ψ(X)≥ψ(Y); 存在一个子集套A1=E⊃A2⊃…⊃An, 使得∀ri∈A, 均有Lri=I|Ai.并∀ri,rj∈A且ri≠rj, 有Lri≠Lrj. 定理9(准模糊图拟阵的导出独立集公理) 设E={x1,x2,…,xm}是非空有限集合, 任取E上的一个子集族L, 数列A={α1,α2,…,αn}(0<α1<α2<…<αn≤1), 满射ϑ: L→A∪{1}.则L,A和ϑ分别是某个准模糊图拟阵的导出独立集族、 基本序列和导出独立集映射的充要条件是L,A和ϑ满足条件(i),(ii),(iii)**和(iv). 证明: 必要性.设L,A和ϑ分别是准模糊图拟阵M=(E,l)的导出独立集族、 基本序列和导出独立集映射.根据文献[7]知,M=(E,l)是闭模糊拟阵.因此, 由定理8知条件(i),(ii),(iii)*和(iv)均成立.再根据条件(iii)*和命题2知, 条件(iii)**也成立. 充分性.此时, L,A和ϑ满足条件(i),(ii),(iii)**和(iv).∀αi,αj∈A,i 由定理7知,M*=(E,l*)的导出拟阵序列是 (E,Lα1)⊃(E,Lα2)⊃…⊃(E,Lαk). 结合命题1知, L=Lα1.再根据条件(iii)**, 存在子集套A1=E⊃A2⊃…⊃An, 使得∀αi∈A, 均有Lαi=L|Ai=Lα1|Ai.根据定理3知,M*=(E,l*)是准模糊图拟阵.证毕. 综上所述, 本文用闭模糊拟阵可由基本序列和导出拟阵序列唯一确定的方法, 提出并证明了一个用导出独立集族、 基本序列和导出独立集映射描述的闭模糊拟阵的充要条件.通过该充要条件任取一个子集族、 一个数列和该子集族到数列的一个满射, 在满足规范性、 继承性、 强单调减和增长性的条件下, 可唯一确定一个闭模糊拟阵, 反之亦然.从而闭模糊拟阵的许多问题都可以转换为子集族、 数列和子集族上的映射.例如, 可以尝试用该方法讨论模糊拟阵的极值问题[10-11]、 模糊横贯拟阵的表示问题[12-16]和模糊拟阵秩的计算问题[17-18]等.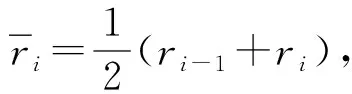
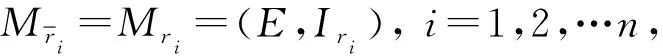
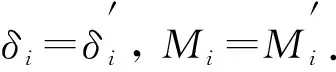
2 导出独立集和导出独立集映射
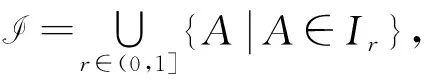
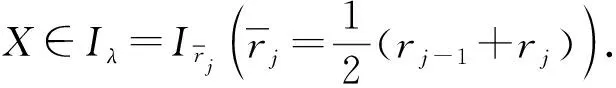
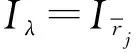




3 闭模糊拟阵的导出独立集公理

