高温混凝土内部温度场计算方法研究

杨海林

（唐山工业职业技术学院，河北 唐山 063299）

近年来，我国建筑火灾频发，给人民财产造成了不可估量的损失。在危害建筑结构的诸多因素中，火灾已成为危害性最大的灾害之一。当前我国的建筑大多采用钢筋混凝土结构，火灾产生的高温环境会使结构内部发生物理化学变化，从而影响结构的受力性能，严重的甚至会造成结构破坏倒塌。结构抗火性能研究是一门复杂的交叉学科，混凝土结构应用于建筑工程的初期没有得到足够的重视，直到1905年美国的ASTM（American Society for Testing and Materials）协会才研究了墙板构件的高温试验方法，但并没有得到广泛应用，直到40年后国际上才对混凝土结构抗火性能重视起来。其中研究较早的国家主要有美国、加拿大、法国、瑞士等，随着大量理论和试验研究的展开，混凝土结构的抗火性能研究等进入到了快速发展阶段。我国在这方面的研究较晚，20世纪60年代公安部的消防研究所和冶金部的建筑研究院等单位才开始了混凝土结构耐火性能研究。20世纪80年代，同济、清华等高校相继建立了高温试验装置，建立了高温下混凝土结构的本构模型，取得了大量的研究成果。火灾发展一般会经历3个阶段，按照先后顺序依次为增长阶段、全盛阶段、衰减阶段，研究高温混凝土的性能首先要研究温度场。

近年来，许多研究人员对温度场进行了大量研究，成果主要有：刘猛等[1]运用ABAQUS建立了混凝土高温框架模型，对构件受力及内部温度场分布规律进行了研究；王勇等[2]通过对常温和高温连续板进行力学试验，分析了钢筋混凝土高温状态下的破坏模式；吴庆良等[3]针对沉管隧道受火前后的变化，应力2次分离变量法，研究了RABT火灾曲线下温度场的求解方法；宋岩升等[4]应用PyroSim分析软件对某宿舍楼火灾进行了模拟，研究了结构内部的温度场分布及内力变形；习阳等[5]应用ANSYS建立了钢壳混凝土模型，对结构不同受火时间下的温度场变化进行了分析。目前对高温下混凝土内部温度场的研究已经有了一定的基础，但缺少更加细致的成果，没有热传导微分方程不同计算方法的对比研究。因此，工程中亟需一种能够快速准确地确定构件火灾时温度场分布的方法。在查阅相关文献的基础上[6-8]，通过大量的理论计算，对建筑火灾过程中温度场随时间的变化规律进行了研究，对3种计算方法的优缺点进行了对比分析，为今后的研究提供了基础。

1 火灾温度-时间曲线

由于火灾发生时温度场变化非常复杂，根据相关统计，地上建筑发生的火灾中，80%在1 h内被扑灭，95%在2 h内被扑灭。为了便于科学研究，国内外许多机构制定了火灾温度随时间变化的标准曲线，这些曲线都是根据大量试验数据绘制的，曲线形态都是单调的升温曲线，升温速率随着时间降低，国际标准化组织ISO（International Organization for Standardization）提出的升温曲线如图1所示，其计算公式见式（1）。

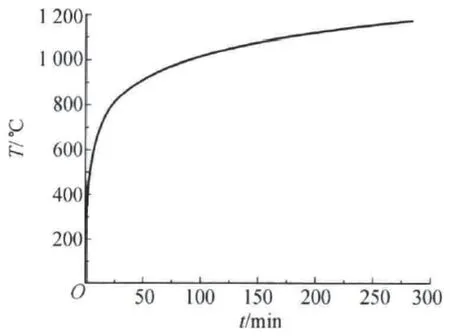
图1 ISO834标准升温曲线

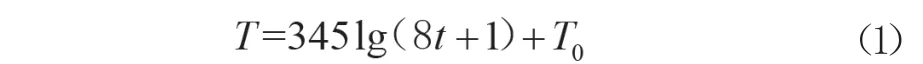
公式（1）中t为火灾发生时间，To（℃）为初始温度，T为火灾发生t分钟后空气的平均温度。

欧洲的Eurocode1规范[9]综合火灾现场各种因素给出了室内温度-时间升温段（t*≤td*）的公式（2）和降温段（t*＞td*）的公式（3）。

式（2）中T（℃）为某一时刻的温度，t*（min）为名义升温时间，td*（min）为名义升温时间最大值，其余含义同公式（1）。

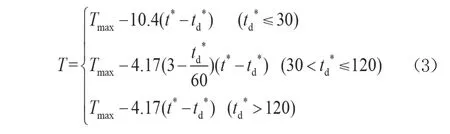
式（3）中Tmax（℃）为最高温度，其余含义同公式（2）。

2 温度场热传导微分方程

2.1 基本方程推导

要想研究火灾对混凝土结构的影响，就要研究火灾发生的任一时刻空间各点的温度分布，但温度场是动态发展的。由于火焰是向上蔓延的，所以建筑受火后楼板和梁的底部为主要受火面，温度发展最快，此时可按公式（1）和公式（2）进行计算。地面和楼面为背火面，短时间内温度不会明显升高，为简化计算，通常按室温计算。

为了分析混凝土内部的热传导，可以建立固体物质的微分方程，假设材料各向同性，且λ（热导率）、c（比热容）、ρ（表观密度）都是T的函数，微元体的热流分析见图2。在如图2所示的直角坐标系中，在任一点（x,y,z）附近取一微元体dx, dy, dz，假设在dx, dy, dz内部温度T均匀分布，某一时刻t的温度为T（x,y,z,t）。

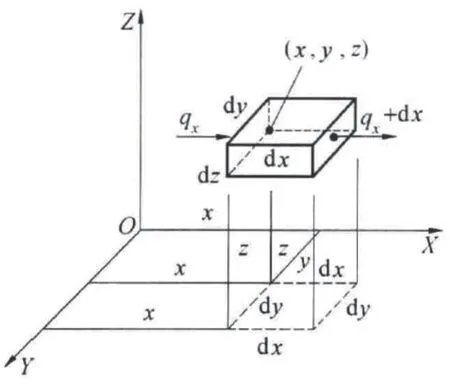
图2 微元体热流分析图

如图2所示，微元体与外部存在热传递，首先研究X轴方向吸收的热量。单位时间单位面积流入微元体的热量为qx，按公式（4）计算，流出的为qx+dx按公式（5）计算。

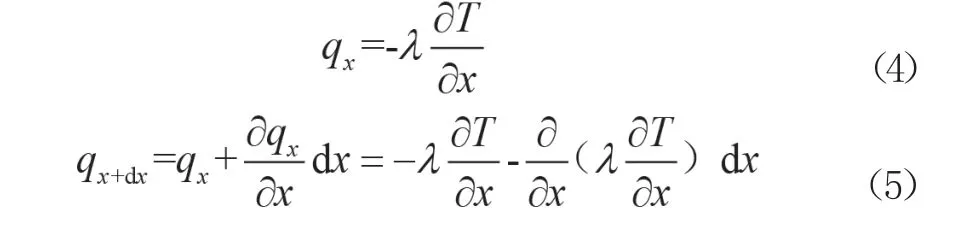
由于微元体平行于YOZ平面的面积为dy·dz，所以单位时间内X轴方向吸收的热量为式（6）。

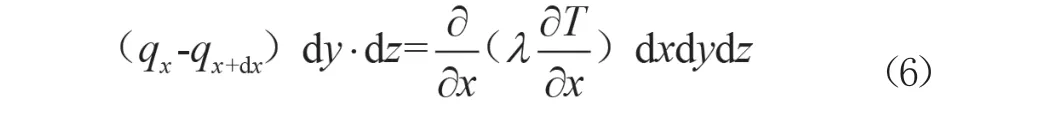
同理在Y轴方向吸收的热量见式（7），在Z轴方向吸收的热量见式（8）。

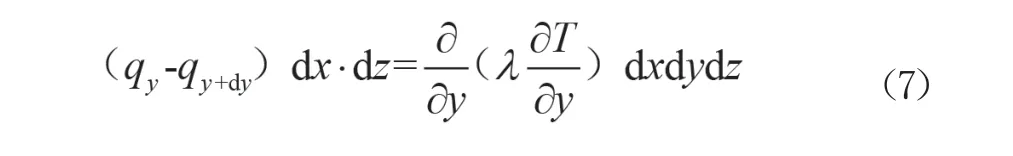
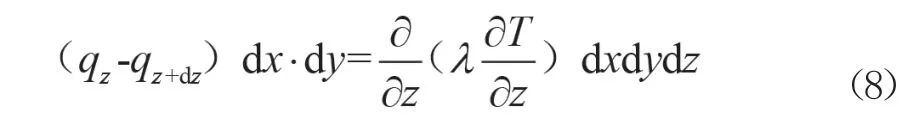
将式（6）、式（7）、式（8）相加可以得到微元体在单位时间内吸收的总热量qA，即公式（9）。

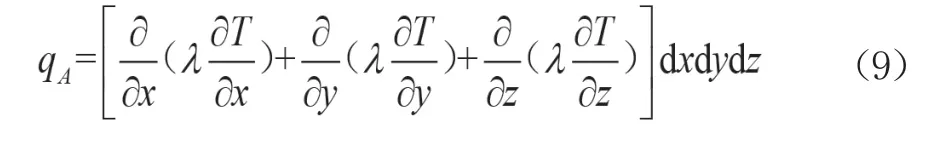
假设一定体积一定时间内材料内部放出的热量为qd，则微元体放热总量为qddxdydz。吸收热量会使微元体温度升高，还可以根据比热容的定义进行计算，即吸收的总热量为（c·pdxdydz）。根据能量守恒，得到式（10）、式（11），即瞬态热传导微分方程。

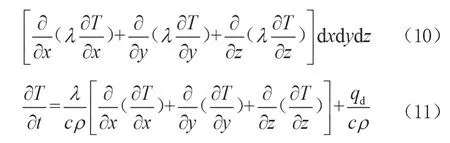
由于混凝土结构自身产生的热量远小于吸收的热量，所以可以简化为qd=0如果构件内部外部温度都不随时间T变化，则公式（11）可简化为公式（12），即得到了稳态热传导微分方程。

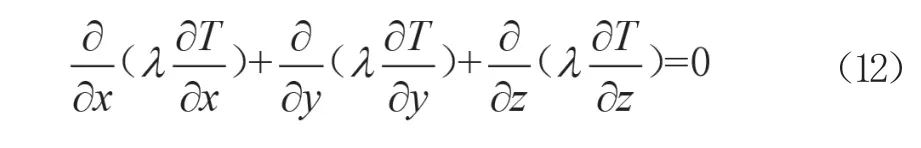
2.2 不同构件的适用情况

不同的混凝土构件试用不同的微分方程，要综合考虑构件类型、维度及状态。杆系结构（如梁、柱等）可以按二维温度场计算，平面结构（如墙、板等）可简化为一维温度场，具体结果见表1。

表1 不同构件的热传导微分方程适用情况汇总

如果材料的导热系数λ不随外界温度变化，可引入常数，其中d(m2/h、m2/s)为材料的热扩散率，可通过热工参数进行推导，将其带入式（11）、式（12），可简化为式（13）、式（14）。

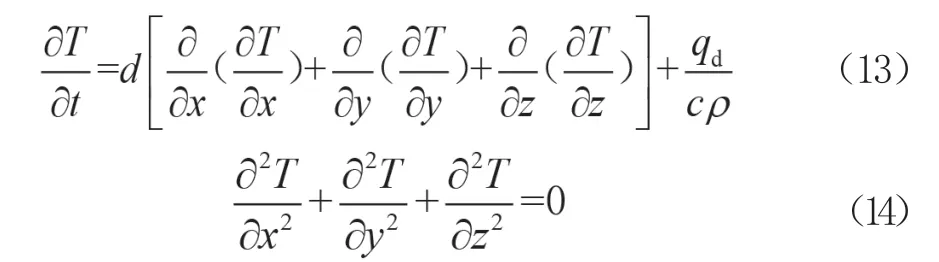
2.3 定解条件和求解方法

要想求解热传导微分方程，还需要得到对应的边界条件，即传热过程中材料与周边热量相互作用的条件。当材料给定时，可以通过试验测得对应的热工参数，包括λ（热导率）、c（比热容）、p（表观密度）等，确定初始和边界条件后就可以对方程进行求解，下面讨论如何确定初始和边界条件。

混凝土结构在火灾发生前一直处于室温状态，内部几乎不存在温差，所以可以将环境温度T0作为初始温度条件，即T(x,y,z,t=0)=T0。

边界条件由于受到外部环境、热传导条件、周边介质等的影响会变得复杂，一般有4种情况。

1）l1（结构边界）上的温度T和时间t存在函数关系，即。

2）l2（结构边界）上的即热流量）和t存在函数关系，其中n为边界的法线方向。

3）结构和流体接触，已知Ta（外部接触的流体温度）和经过l3（边界）上的热流量，即，其中βT为传热系数，单位W/(m2·K)。

4)结构和固体接触，已知l4上的热交换条件，受火面可按式（15）计算，其中α(W·m-2·℃-1)为换热系数，为结构表面温度，Te(℃)为环境温度。具体到混凝土结构，可将式（15）换算成式（16），其中hc(W·m-2·℃-1)为对流换热系数，hr(W·m-2·℃-1)为辐射换热系数， =5.67×10-8W·m-2·℃-4。

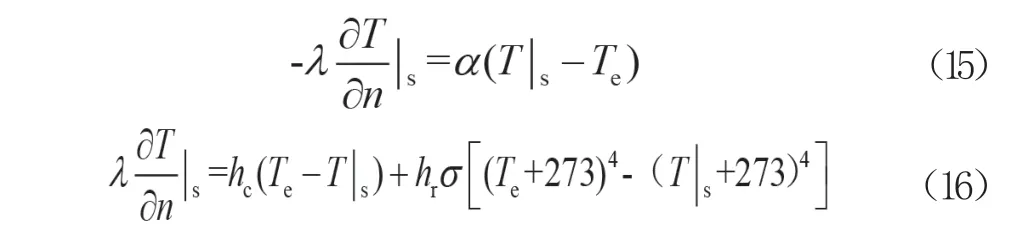
实际工程中为了简化计算，可将hr换算成hc，将辐射影响计算到α（综合换热系数）内，即简化为公式（17）,其中K(W·m-2·℃-1)为传热系数，α可按表2选用，为了便于计算任一温度下的α值，将表2中数据进行拟合，见图3。

表2 综合换热系数α(W·m-2·℃-1)选用表

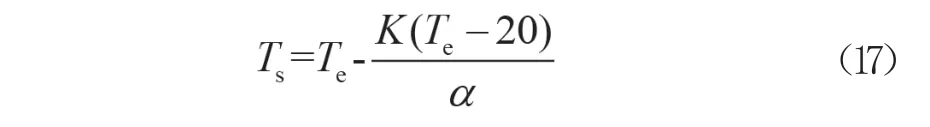
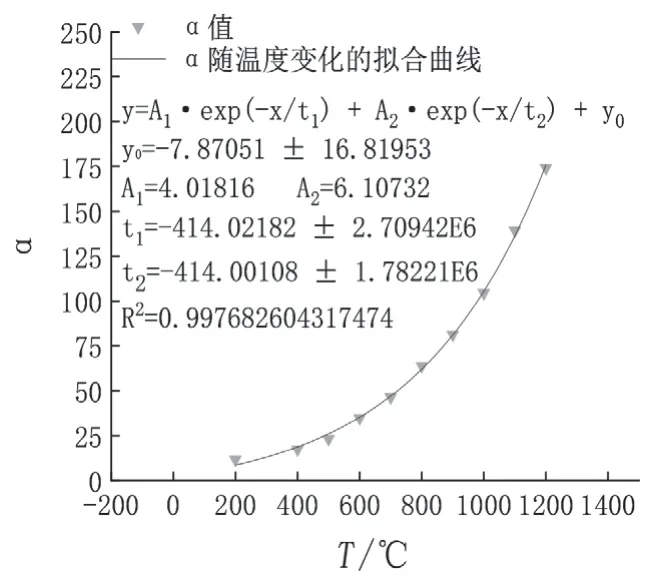
图3 换热系数α随火焰温度变化图

采用Origin中的ExpDec2进行拟合，发现R2达到了0.99768，表明拟合相关性较好。根据图3的拟合结果，可以得到任一T下α的值，用于火灾发生时受火面的温度场计算，为了简化计算，背火面通常取室温。

3 求解方法

热传导微分方程为二阶偏微分方程，对其求解的方法主要有以下3类。

3.1 解析法

为了简化计算，通常假定混凝土材料内部是各向同性、连续、内部不发热的，由于内部钢筋占比较少，通常不考虑其影响，工程中的板和梁高跨比较大，通常简化为无限大板和无限长梁，此时公式（13）就可以简化为一维或二维问题，即式（18）。

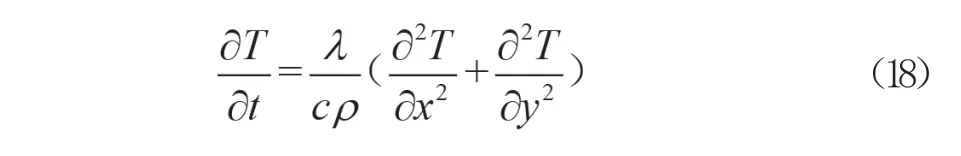
假定初始温度为20℃，由式（18）和式（15）组成方程组，即式（19）。

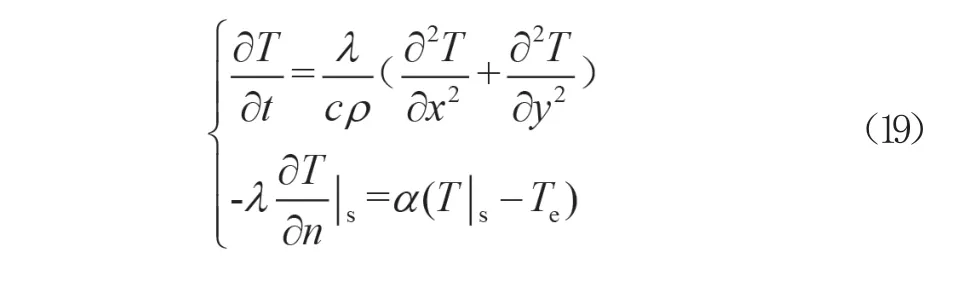
对于无限大平板，可进行拉普拉斯变换得到式（20），其中y为受火面到内部的垂直距离，erf(x)为高斯误差函数，可查表获得，=1/（pc）（m2/s）为导温系数。

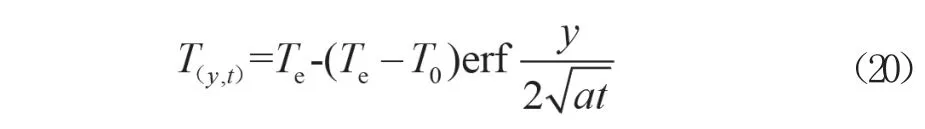
此外还可以将受火面，即y=0时的温度变化简化为正弦函数，采用分离变量法求解，即式（21），其中T'max为温度增量的最大值。

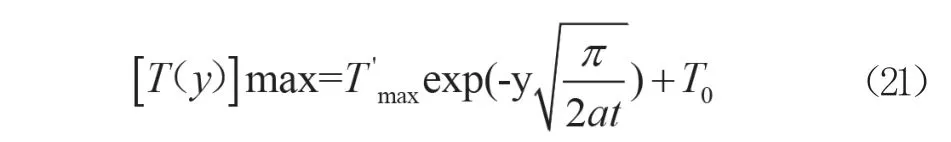
值得注意的是，式（20）和式（21）由于做了大量简化计算，只适用于初步粗算，达不到较高精度。

3.2 差分法

对于形状规则边界简单的结构，可以用差分代替微分，同时考虑节点作用，达到减小计算量的目的，二维状态下的温度场网格划分见图4，显示差分方程可表示为式（22）。

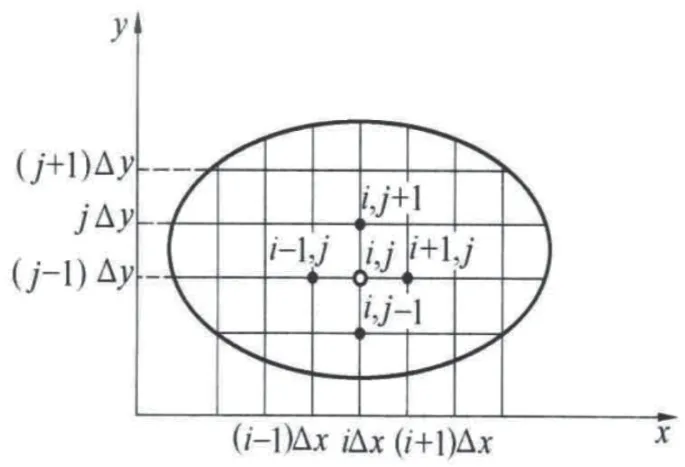
图4 二维温度场差分法网格划分示意图

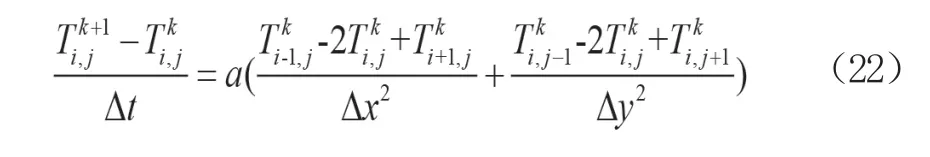
对式（22）进行求解可采用泛函数求极值的方法，用欧拉方程求解得到极值曲线。采用泛函极值条件的二点差分热传导方程可表示为式（23），式中[K]、[N]、[P]为温度矩阵，{T}t为待解温度列向量，{T}t-△t为上一时刻列向量。应用式（23）可依次求得间隔△t各时刻的温度场。为了简化计算程序，后期步长可适当放大，同时放大背火面步长。

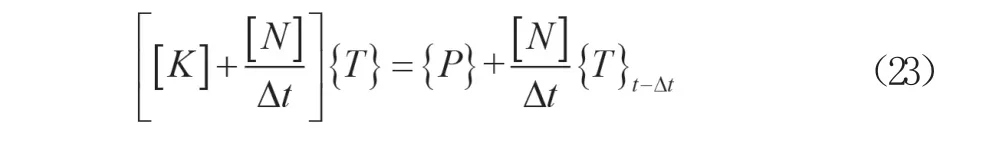
在实际工程中，还要综合考虑火灾发生时混凝土内部水分的影响，为了简化分析，通常将这些水分的影响综合到α、λ、c、p中进行计算。综上，给定边界条件的情况下，截面形状规则的构件（如三角形、矩形、正方形）应用差分法求解温度场具有较高的精度，此方法计算灵活，速度较快，但不适于处理复杂形状的构件。

3.3 有限元-差分法

有限元-差分法目前应用广泛，可用于求解任意时刻的温度场问题，包含两个部分，即空域采用有限元法，时域采用差分法。目前的大型软件如ANSYS、ABAQUS等都可进行有限元-差分法的运算，计算时沿时间方向递推进行迭代运算，分析软件会自动根据迭代情况进行收敛。为了简化计算，将瞬态热传导微分方程构造成公式（24）所示的线性函数，其中{T}为温度向量，{Pβ}为热载荷向量，[c]为热容矩阵，[K]为总导热矩阵。进行计算时，可先给定收敛容许值Tg，当时运算停止。

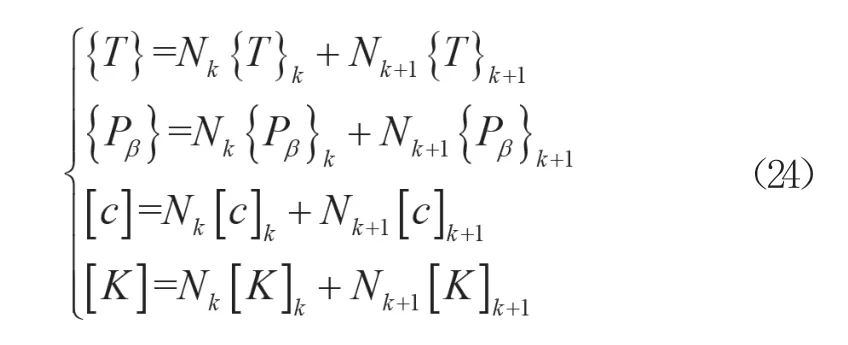
式（24）中，Nk=1-ξ，Nk+1=ξ，ξ=τ/△tk且0≤ξ≤1。对式（24）中的{T}求时间t的偏导可得式（25）。

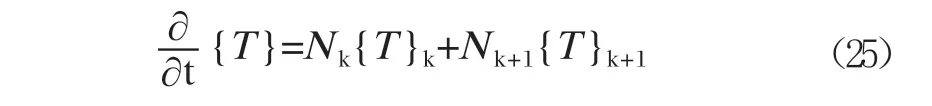
如图1所示，标准升温曲线为对数函数，温度升高速率逐渐降低，这与构件温度场的升温规律相近。当升温速率较大时（即升温初期），运算过程中的振荡剧烈，反之（即升温末期）振荡趋于平缓，为了提高运算效率，可以随温度升高适当延长步长，进行变步长运算。

式（24）与式（25）可以用于瞬态热传导的求解，除此之外还有稳态热传导，下面介绍稳态热传导微分方程的解法，方程见式（26）。

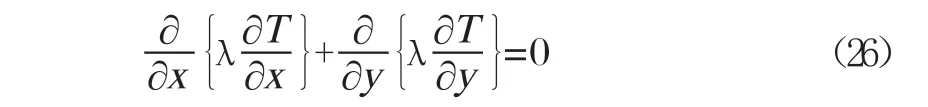
式（26）为一个椭圆形的偏微分方程，稳态热传导问题本质上可以看作瞬态热传导问题的特殊情况，即时间无限长且温度恒定时的情况。这类方程可以采用多种方法进行求解，过程较瞬态要简单得多，常用方法是通过求解一系列线性方程组来逼近真实解，工程中应用较多的是Newton-Raphson法和修正Newton-Raphson法。

综上，有限元-差分法综合了两种计算方法，适用性更强，可用于求解非线性偏微分方程，即瞬态温度场分布情况，可以根据计算机配置情况及工程需要合理选择计算精度，可用于求解高温混凝土内部温度场。但这种计算方法也是具有一定的局限性的，很难同时保证稳定性和精度要求。运用两点后差分方法进行计算时能够保证计算过程的稳定性，可以避免无效振荡，但计算结果精度不高。Crank-Nicolson方法、Galerkin方法以及三点后差分法可以在满足稳定性的同时提高计算精度，缺点是对单元尺寸和时间步长的选择要求较高，求解过程容易发生振荡，为了克服无效振荡，通常需要进行变步长运算，过程较复杂。

4 结论

运用理论计算研究了高温状态下混凝土内部的温度场分布情况，总结了火灾过程中的升温曲线变化规律，推导了热传导微分方程，比较了求解的三种方法，得出以下结论:1）升温曲线为对数函数，初期升温速率较快，后期趋于平缓；2）杆系结构可简化为二维温度场进行计算，平面结构可简化为一维温度场；3）实际工程中通常将各复杂情况考虑到综合换热系数中进行计算，通过软件拟合，得到了综合换热系数和火焰温度的关系曲线；4）对比三种求解方法，发现有限元-差分法适用各种复杂工况条件，可用于高温状态下混凝土内部温度场计算。