采用光纤光栅级联结构实现光纤延迟线

王 翀，杜 欢，王 静，王 菁，王景华

西安邮电大学电子工程学院，陕西 西安 710121

引 言

光纤延迟线作为光分组的存储设备和缓冲器[1]，被广泛应用于光通信、 全光信号处理、 相控阵雷达天线以及微波产生系统中[2]，具有损耗低、 体积小、 易于集成、 带宽大、 抗电磁干扰等优点[3-4]。 光纤延迟线的研究一般通过几个特征来实现： 一是连续可调性，二是使用相对较短的光学长度最大程度地减少延迟，三是同时访问一个或多个可能的延迟值[5]。 近年来，人们利用各种光学元件来制作光纤延迟线，常用到单模光纤、 色散补偿光纤、 光纤布拉格光栅、 集成波导或光子晶体波导[6-7]等，而光纤光栅型延迟线的研究成为一大热点。

光纤布拉格光栅作为一种重要的光学滤波器件，广泛应用于传感器、 通信、 色散控制和光子信号处理器中[8-9]。 它是一种有效折射率沿长度周期性变化的波导结构，由于这种周期性的指数变化，可以使其反射特定波长的光，因此可作为特定波长的反射器或过滤器[10]。 在光纤延迟线中，通常会利用光纤光栅的反射镜作用、 群时延作用或者温度应变能力达到延时目的。 2018年, Zhao[11]等提出一种基于线性啁啾光纤布拉格光栅的可配置光子真时延迟线，利用光纤光栅的群时延特性，控制波长为1 549.92，1 551.72，1 552.52和1 553.33 nm的光信号经过8个串联啁啾布拉格光栅，实现了104 ps的延迟，这种延迟线虽然中心波长间距小，但时延范围只有皮秒级别； 2019年，Ao[12]等提出一种基于光波导带布拉格光栅的光纤延迟线，这种延迟线使用布拉格反射器和延迟波导组成延迟波导单元，实现了中心波长范围为1 560～1 584.5 nm、 间距为3.5 nm、 单步长为12.5 ps的延迟，这种结构延迟线能够将一路传输光纤多次使用，但中心波长间距大。

在此基础上提出了一种光纤光栅与单模传输光纤相结合的级联结构，可以实现中心波长范围为1 550～1 553 nm、 间距为1 nm、 单步长为0.5 μs的延迟线，即能使中心波长间距变为1 nm的窄带，又能使一路传输光纤被多次使用的微秒级别时延。

1 系统构成及工作原理

1.1 光纤延迟线的系统构成

光纤延迟线系统包括六部分，分别为： 可调谐激光光源(TUNICS T100S-HP高功率可调谐激光器)、 DWDM密集波分复用器、 EDFA光纤放大器、 光延迟模块、 波分解复用器(DE-DWDM)以及光探测器[11]。 如图1所示，其中，可调谐激光器发射的波长范围为1 500～1 630 nm，本文选择1 550，1 551，1 552和1 553 nm这四个波长，经密集波分复用器后由单根光纤传输至光纤放大器，完成对光信号的放大，之后由光延迟模块对不同波长的光信号进行相应时延，最后由波分解复用器将延迟后的信号分为四路从光探测器输出。

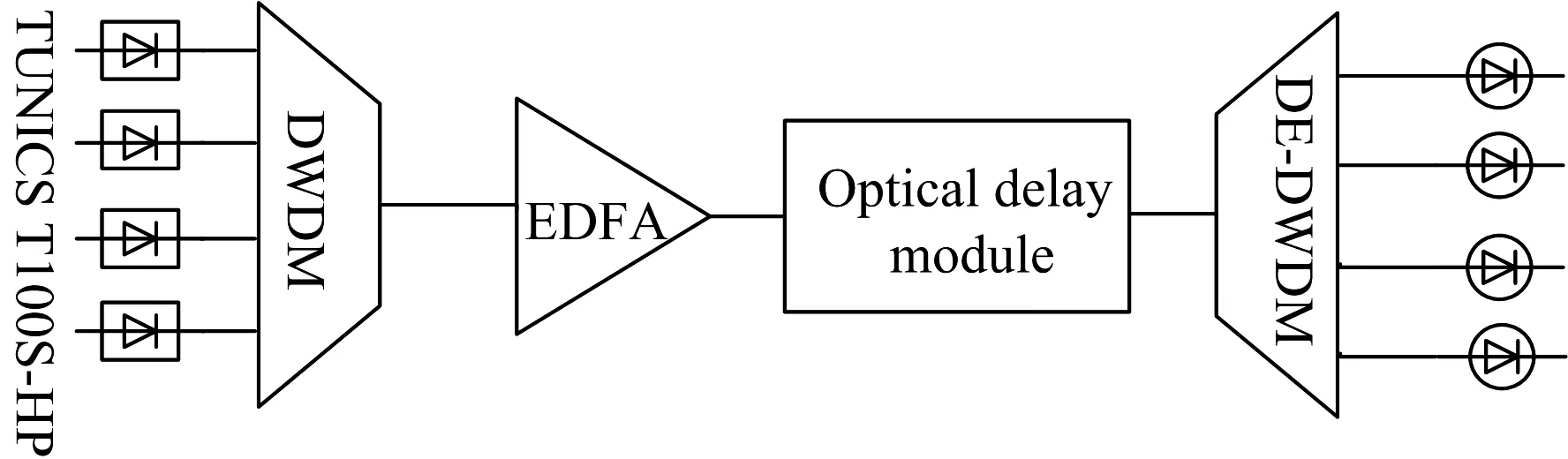
图1 系统框图Fig.1 Block diagram of system

1.2 原理及延迟模块设计

光在传输光纤中传播时，满足式(1)，时延大小Δt会随传输光纤长度L的增大而增大，也就是说只要改变光纤长度就能实现不同的延迟时间。

(1)

式(1)中，ng为光纤的群折射率。 输入信号与输出信号仅发生时间延迟，但其频率、 幅度等特性不发生改变。

因此，采用传输光纤完成光信号的时延，光延迟模块由单模传输光纤、 光纤光栅、 光环形器这三大部分构成，如图2所示，采用光纤光栅级联结构可以使每一路传输光纤被多次使用，从而减少传输光纤的数量。 每个延迟单元由相同长度的传输光纤与特定波长反射啁啾布拉格光纤光栅连接而成，再使用光环形器将4个延迟单元级联构成光延迟模块，每个光栅的啁啾系数相同，只是光纤光栅反射光信号的特定波长不同。 每个延迟单元的延迟步长均为103 m，单次通过可实现0.5 μs的时延，所以该系统可实现1，1.5，2和2.5 μs四种不同的时延。

图2 光延迟模块框图Fig.2 Block diagram of optical delay module

1.3 光纤绕线盘

随着信道容量和比特率的增加，传输线的复杂度和成本也随之增加，对于某些应用，即使是最简单的体积和重量也成为了关键因素。 在此次延迟模块的设计中，由于所使用的单模传输光纤有四段，且每段长为103 m，在使用时会被反复弯曲，为了避免传输光纤松动，将四段传输光纤更好的整合，并且尽量减小延迟模块体积，因此使用光纤绕线盘对延迟单元的体积进行压缩。 此处使用的光纤绕线盘内径6 cm，外径10 cm，高11 cm，如图3所示，其中1～4为四个延迟单元，5～8为光纤光栅，9～12为光环形器。

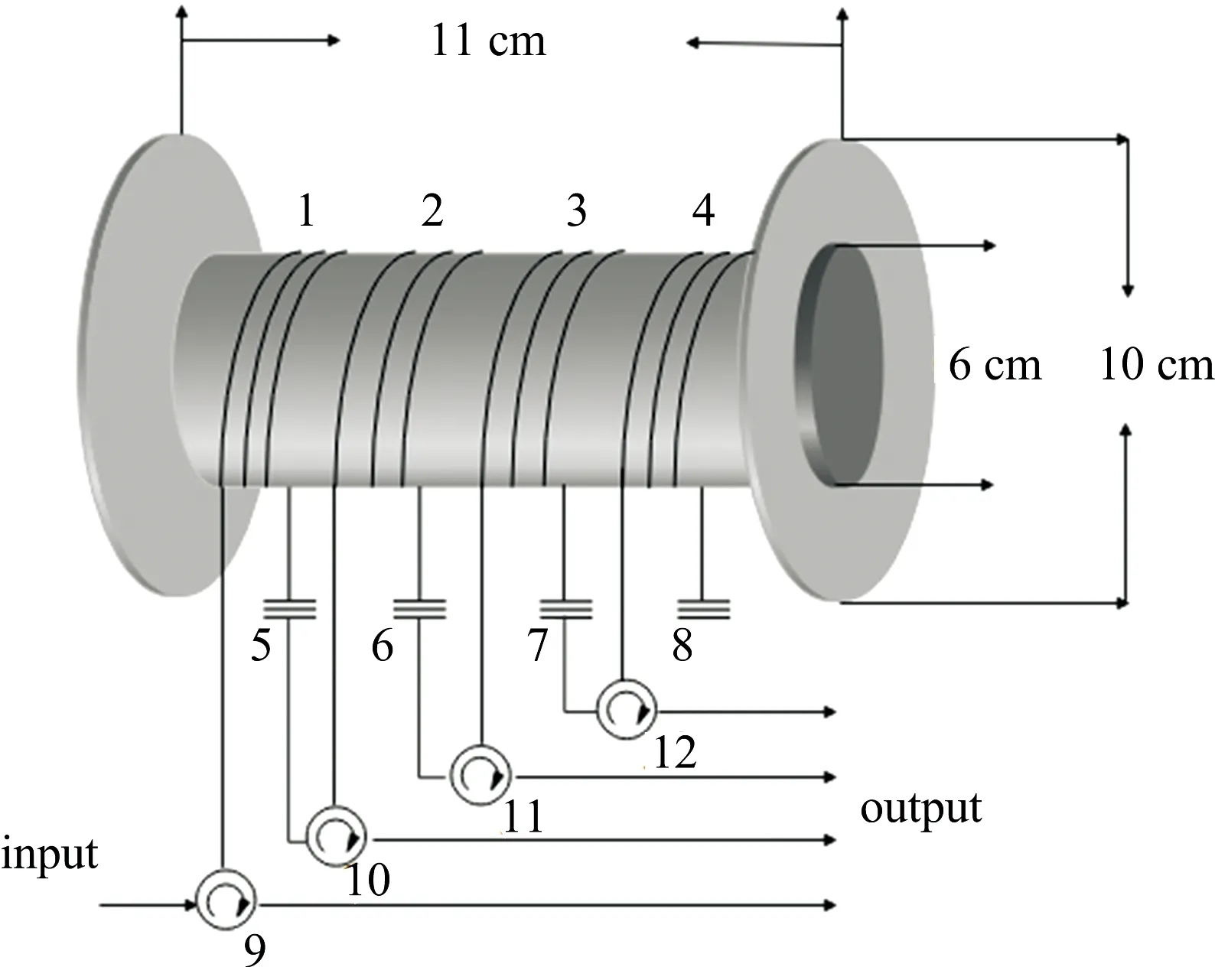
图3 光纤绕线盘Fig.3 Optical fiber reel

2 计算与仿真分析

2.1 布拉格光栅反射谱

光纤布拉格光栅是一种内联光学滤光器，它可以反射特定波长的光，同时传输其他波长的光[13]。 光信号经光纤光栅传输，在到达特定波长λ处发生反射，如图4所示，Λ(z)表示光栅的折射率变化周期。

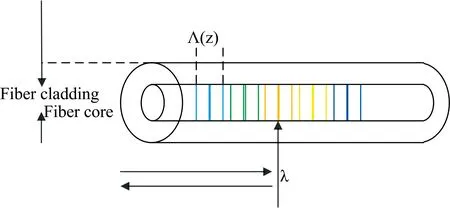
图4 光纤光栅示意图Fig.4 Schematic diagram of fiber grating

在均匀分布的布拉格光纤光栅中，反射率满足式(2)

(2)

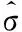
由于延迟模块所使用的光纤光栅只对单波长有反射作用，经过图5的仿真可以发现，光纤光栅结果并不理想，因此采用几个切趾函数对反射谱旁瓣进行抑制。 仿真结果如图6所示，虽然不同切趾函数对反射谱的影响不同，但都在一

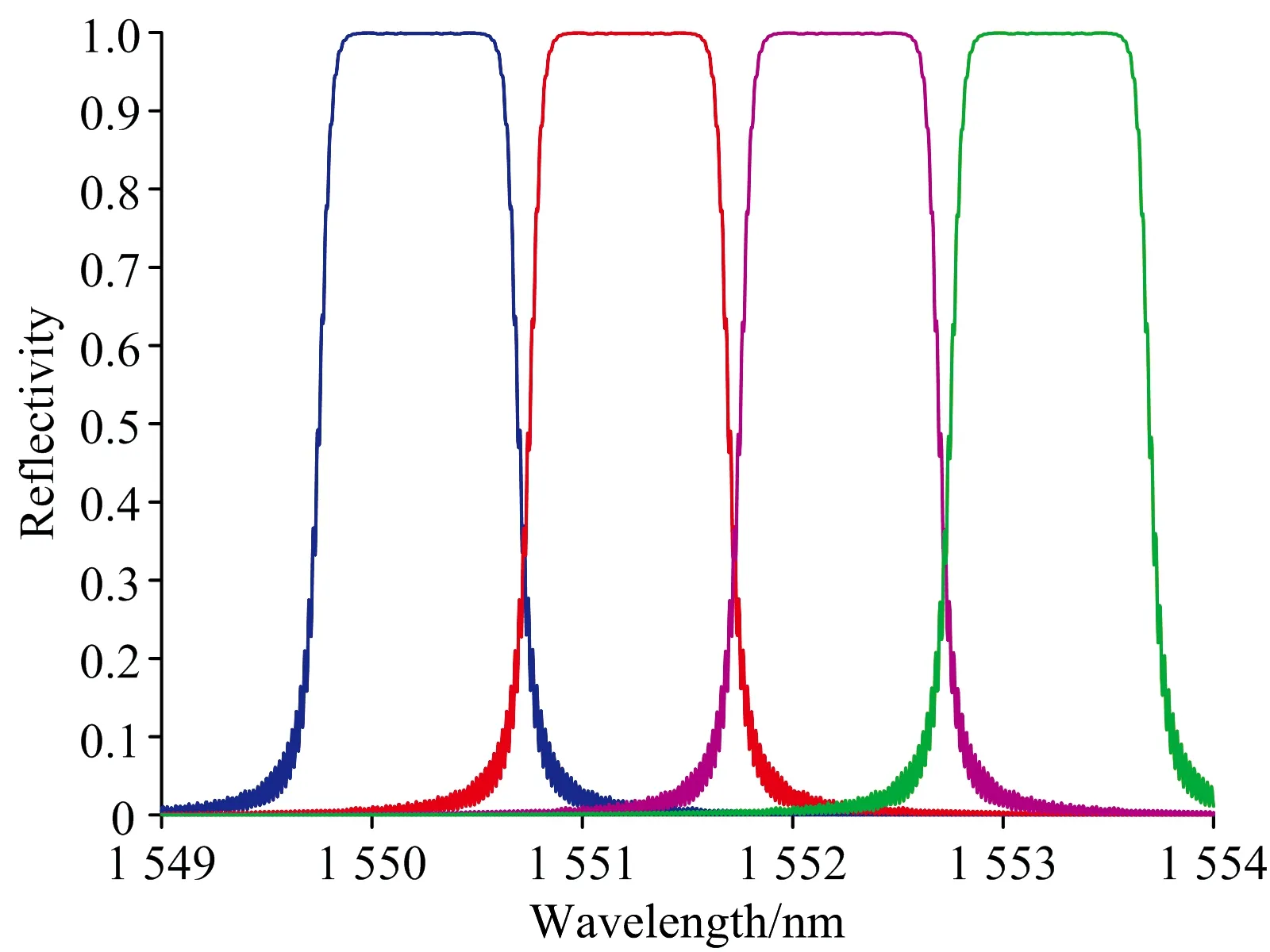
图5 中心波长1 550，1 551，1 552和1 553 nm的反射谱Fig.5 Reflectance spectrum of center wavelength1 550, 1 551, 1 552 and 1 553 nm

图6 六个切趾函数切趾图(a): 布莱克曼函数； (b): 辛格函数； (c): 双曲正切函数； (d): 汉明函数； (e): 高斯函数； (f): 柯西函数Fig.6 Six apodization function apodization diagram(a): Blackman function; (b): Sinc function; (c): Tanh function; (d): Hamming function; (e): Gauss function; (f): Cauchy function

定程度上消减了反射谱带宽，经对比可知，布莱克曼函数、 双曲正切函数和辛格函数都不能达到消除反射谱旁瓣的作用，汉明函数在基本消除反射谱旁瓣的同时严重消减了反射谱包络，高斯函数和柯西函数能够完全消除旁瓣，但都对反射谱包络产生了消减，其中既能完全消除反射谱旁瓣，又对反射谱包络影响最小的是柯西切趾函数。

表1 不同切趾函数对比Table 1 Comparison of different apodization functions

2.2 弯曲损耗

使用光纤绕线盘整合传输光纤时，会产生相应的弯曲损耗，主要是由从直波导进入弯曲波导时产生的模式耦合损耗引起的[14]。 而弯曲损耗的计算方法十分繁多，此处考虑到不同工作波长及弯曲半径的影响，故而采用Luc B Jeunhomme 理论仿真其弯曲损耗，如图7所示。

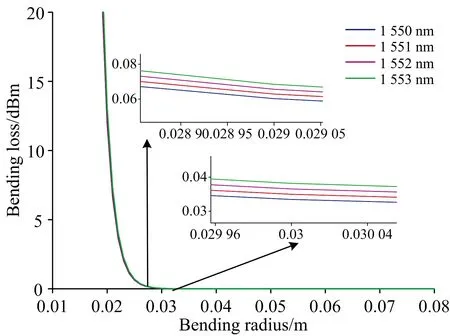
图7 不同工作波长下光纤损耗随半径的变化Fig.7 Variation of fiber loss with radiusunder different working wavelengths

单位弧长上弯曲损耗αR满足式(3)，其中R为弯曲半径，kl(w)为一阶第二类修正贝赛尔函数，w为径向归一化衰减常数，ν为归一化频率，β为光沿轴向传播系数，α为纤芯半径。

(3)

由仿真结果可知，弯曲半径相同时，损耗与工作波长成正比； 工作波长相同时，弯曲损耗与弯曲半径成反比。 在2～2.9 cm范围内曲线快速下降，大于2.9 cm以后较为平缓且趋近于零，所以使用的光纤绕线盘内半径应大于2.9 cm，才能避免由弯曲带来的损耗，因此选用内半径为3 cm的光纤绕线盘对延迟模块传输光纤进行体积压缩。

3 实验测试

3.1 延迟波形测试

由于在延迟单元中通过使用一定长度的传输光纤达到时延目的，故而在实验测试过程中，最重要的是须确保光信号经过不同传输距离后所产生的损耗最小，因此在工作波长与弯曲半径保持不变的情况下，当光纤长度分别为0 m，3 m和5 km时对输出信号的波形进行测量，测试框图如图8所示。 采用GY-IB型手持式激光光源提供1 550 nm的输出光信号，光波经过特定长度的传输光纤之后，利用泰克TDS784D型示波器对频率为2 000 Hz的输出波形进行测量，如图9所示。

将一定长度的传输光纤绕成内半径为8.25 cm的绕线盘，中心波长1 550 nm，频率2 000 Hz的光信号直接输入示波器中测得周期为500 μs、 相位144°、 信号带宽500 MHz、 脉冲宽度为200 μs； 经3 m和5 km传输线后各项参数均保持不变。 由测试结果可知，经5 km长距离延迟后的信号依然能保持原信号的特征，因此使用103 m传输光纤可达到预期延迟目的。

3.2 弯曲损耗测试

由于使用弯曲半径为3 cm的绕线盘对延迟单元中的传输光纤进行整合，为了检测弯曲半径是否合理，因此对中心波长为1 550 nm, 传输光纤总长度为3 cm，但弯曲半径不同的情况下对输出功率进行测量，并绘制输出频率为2 000 Hz时不同弯曲半径下相对于直光纤的功率差曲线图(图11)。 采用GY-IB型手持式激光光源提供1 550 nm的输出光信号、 3 m传输光纤以及W-GGL型光功率计对不同频率下的输出功率进行测量。

结果显示，光纤的弯曲程度会对输出功率造成不同程度的损耗，当弯曲半径处于2～3 cm时，输出频率在1 000与2 000 Hz处有较大损耗，当弯曲半径大于3 cm时输出功率无限趋近于直光纤的输出功率，经计算在弯曲半径为3 cm处相对于直光纤的输出功率相差0.18 dBm，因此设置绕线盘内径为3 cm符合光纤延迟线的损耗范围。

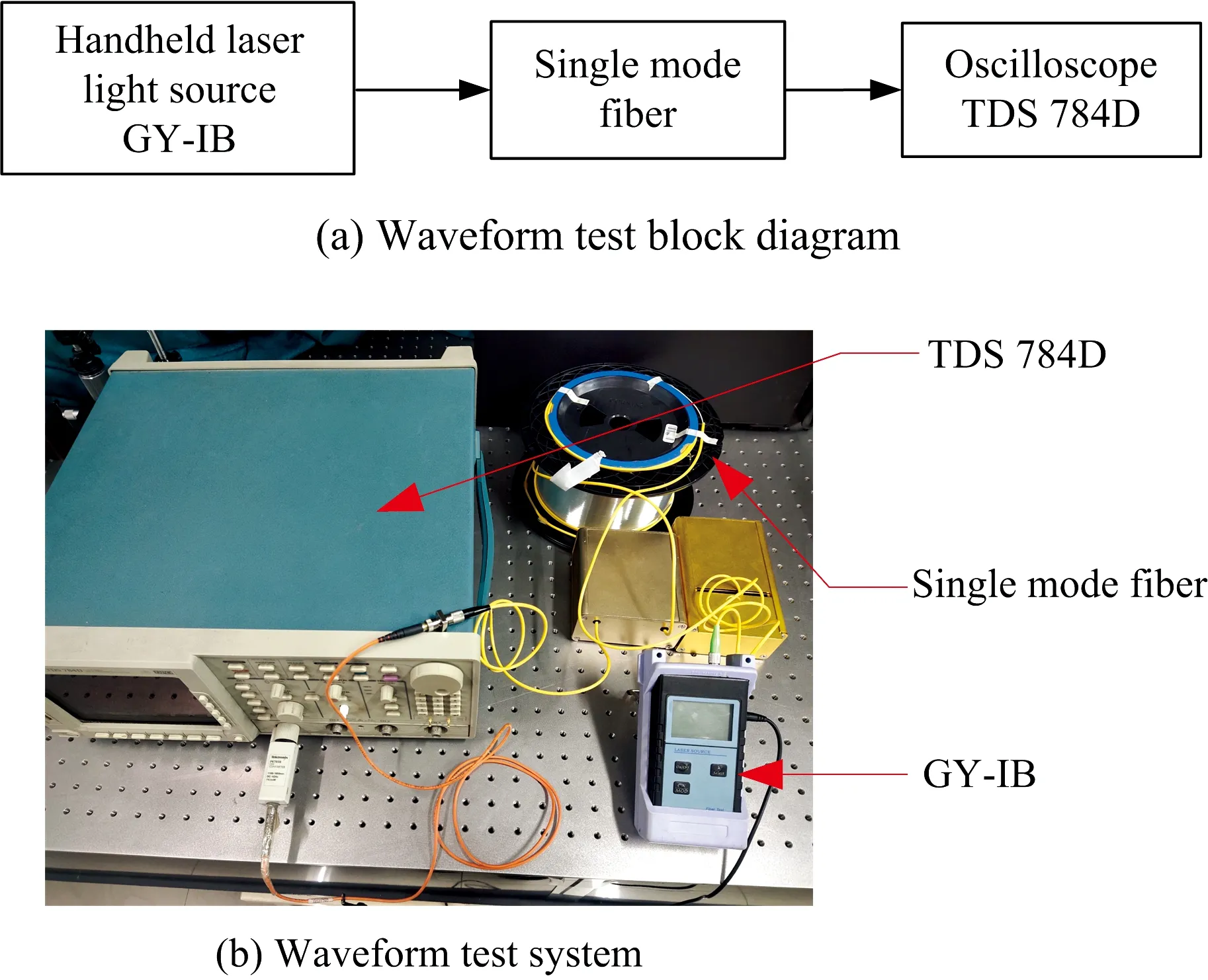
图8 波形测试系统Fig.8 Waveform test system

图9 输出频率为2 000 Hz时不同传输距离波形Fig.9 Waveforms of different transmission distances when the output frequency is 2 000 Hz

图10 测试系统框图Fig.10 Block diagram of the test system

图11 输出频率2 000 Hz时相对于直光纤的功率差Fig.11 The power difference relative to the straight opticalfiber when the output frequency is 2 000 Hz

4 结 论

根据大范围可调光纤延迟线的基本要求，使用光延迟单元级联结构，不仅能将光纤光栅型延迟线时延范围提升到微秒级别，而且还实现了中心波长宽度为1 nm的窄波长反射型时延线，也能减少传输光纤的使用。 本文对光纤的弯曲损耗以及中心波长不同的啁啾布拉格光纤光栅的反射谱进行仿真分析，由于反射谱旁瓣产生重叠现象，并没有达到预期效果，因此需采用不同的切趾函数对光纤光栅反射谱的旁瓣进行滤除。 仿真结果表明： 采用不同的切趾函数对反射谱的旁瓣滤除效果不同，能够完全滤除旁瓣并且对反射谱包络影响最小的是柯西切趾函数，经柯西切趾后在中心波长1 nm范围内反射率可达到1并且其他波长范围均为0； 工作波长与弯曲损耗成正比，当弯曲半径大于2.9 cm时，弯曲损耗曲线变化平缓且值接近于零。 经实验验证，经过5 km长距离传输后依然保持原信号特征，因此，选用103 m的传输光纤达到相应时延范围是可行的； 弯曲半径为3 cm时，输出光功率与直光纤的输出功率相近，损耗为0.18 dBm，因此，选用3 cm作为弯曲半径可满足损耗低的要求。