基于换热单元非均匀流动的换热器整体等效计算方法研究

刘凯华，傅佳宏，陈晓飞，孙晓霞，张 宇，刘震涛

（1.浙江大学 动力机械及车辆工程研究所，杭州 310063；2.浙大城市学院 机械电子工程学系，杭州 310015；3.浙江银轮机械股份有限公司，台州 317200；4.中国北方发动机研究所，天津 300400；5.中国北方车辆研究所，北京 100072）

0 概述

为了在提高车用换热器的换热效率的同时减小换热器的体积，换热器的换热单元、翅片向小尺寸发展［1-2］。在此背景下，紧凑式换热器（compact heat exchanger）、微通道换热器（micro-channel heat exchanger）等问世。

紧凑式换热器内部结构尺寸与换热器整体的尺寸跨度达到了2～3 个数量级。在分析含有小尺寸内部结构的换热器时应保证每个流道的计算网格精确，而跨尺寸的存在会导致整个换热器的网格数量非常庞大，换热器整体网格数量可达到108数量级，非常耗费计算资源和计算时间。

对于如中冷器、车用水箱散热器等单流程的换热器，研究中用到较多的数值模拟方法主要包括换热器单元模型、周期模型、多孔介质模型及整体模型。文献［3］中以管壳式换热器为对象，对上述4 种换热器计算模型进行了数值模拟计算及试验验证，结果表明多孔介质模型与整体模型的预测精度较高；单元模型和周期模型［4-5］更适用于流动形式单一的换热器；整体模型需要包含所有翅片细节，更适用于内部结构复杂程度不高的换热器。多孔介质模型较容易使用，被广泛接受；文献［6-7］中应用多孔介质来研究油冷器的流动换热性能，文献［6］中采用了试验关联式，而文献［7］中则将换热器内部传热系数设为常数；文献［8-9］中使用重叠网格（dual cell）进行换热器整体的模拟研究，结果显示该方法获得的结果基本与试验结果相符，但换热性能过于依赖经验公式；文献［10-13］中使用换热器模型进行换热器的数值研究，其结果误差较小，但该方法得到的结果同样依赖于试验数据。除上述的数值计算模型外，多尺度耦合方法也被较为广泛地应用于换热器的流动换热计算中［14-15］，该方法能提供较高的计算精度，但计算方法较为复杂且计算量较大。

为解决跨尺度计算中的问题，现有的换热器模型中，多孔介质模型因其计算效率高及准确度较高而被广泛采用。但是，现有的多孔介质模型中流动参数与换热参数需要依赖于大量试验数据、经验公式，而在新换热器、翅片开发过程中缺乏试验数据的支撑。为了在设计过程中为换热器整体换热性能及流动阻力提供依据，提出一种基于换热单元模型的换热器等效数值模拟方法，该方法能在不依赖试验数据的条件下保证较高的计算精度，且减少计算资源，为复杂换热器设计提供依据。

1 研究对象

本文中油冷器的翅片结构见图1，为错齿翅片（offset strip fin，OSF）。围绕该翅片，文献［16-17］中从试验角度进行了大量研究，文献［18-19］中从数值模拟的角度对翅片性能进行了研究分析，文献［20］中则从理论角度对翅片进行了详尽分析，文献［21］中对错齿翅片的经验公式、单相流、两相流等方面进行了研究总结，这些研究为翅片单元性能的计算提供了理论基础。以图2 所示车用油冷器作为研究对象，其中冷却液腔7 层，机油腔6 层，每层腔体厚度约2 mm，换热芯体尺寸约为90 mm×60 mm×35 mm，流道水力直径在1.48 mm～2.00 mm 之间，翅片厚度则在0.15 mm～0.25 mm 之间。如图2（a）所示，冷却液由上进入油冷器，而油则从下进入油冷器，两侧均流经油冷器内部翅片并进行热量交换，最后冷却液和油分别从油冷器左侧上口、下口流出油冷器，完成机油冷却过程。图3 为冷热侧翅片布置图，油冷器内部冷热侧错齿翅片相互交错90°布置，遍布于冷热两侧每一层腔体。

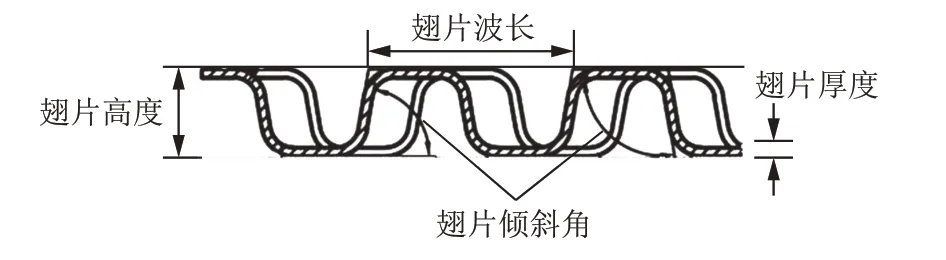
图1 错齿翅片几何结构

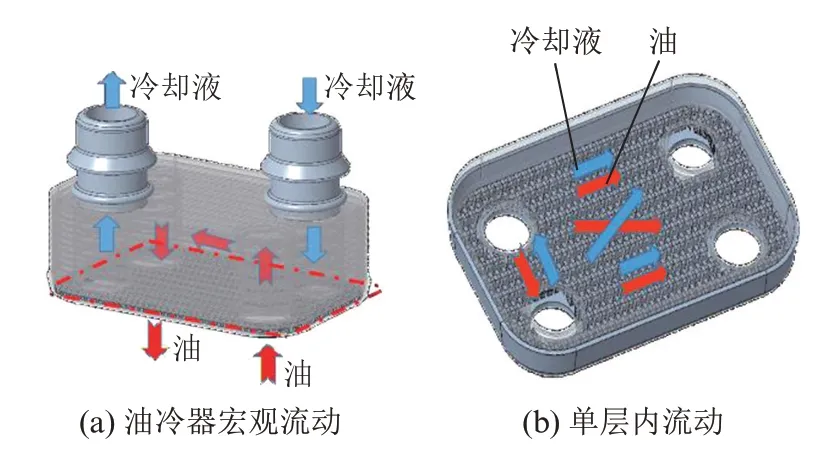
图2 油冷器几何外形及内部流动示意图

图3 冷热侧翅片布置图

2 油冷器等效计算方法

油冷器等效模拟方法如图4 所示。为减少对试验的依赖，该方法分别从换热单元流动换热模拟结果中提取单元模型的流动、换热参数，并拟合为速度关系式，最后将流动、换热参数分别以多孔介质参数与能量源项的形式带入重叠网络的油冷器整体模型中进行计算。

图4 油冷器等效模拟方法

Fluent 软件中自带的重叠网络［8-9］换热器模型可以同时考虑换热器内部流动特性及换热特性，通过较粗的计算网格得到较高的计算精度。该模型将换热器芯体简化为两份位置和体积完全一样的网格，每份网格被设置为多孔介质，从而可忽略换热器内部翅片的具体几何结构，而该模型的换热特性则依赖于换热器整体的试验数据。为了减少换热器性能计算对试验数据的依赖性，本文中对油冷器的计算将仅采用上述dual cell 的网格结构，使用多孔介质参数来描述油冷器芯体的流动属性，而换热特性将以源项的形式加入能量方程，从而达到流动与换热耦合的目的。

由于油冷器冷、热侧介质进出口分布于四角，且冷、热侧翅片交错90°布置，导致其内部流动复杂，如图2（b）所示，每层腔体不同位置将出现顺流、逆流及交错流，换热模式也较为复杂。此外，翅片板流动阻力各向异性也导致了高、低阻力流动的存在。基于上述原因，需要分别针对高、低压流动及不同换热模式进行单独分析讨论，以确定油冷器内部冷、热侧流动换热参数。

2.1 油冷器单元模型

详细的流动参数和换热性能参数是油冷器整体模型计算的依据，而这些参数如单位长度压降、冷侧及热侧传热系数、单位体积传热面积等需要依靠单元模型进行数值计算得到。单元模型如图5 所示：图5（a）为换热单元模型，取热侧完整流道和冷侧上下各一半流道；图5（b）为流动单元模型，包含完整的冷、热两侧流道。为了计算得到较为贴近真实值的换热单元流场与温度场，换热单元包含详尽的几何特征，与实际流道结构一致。且在进行单元分析时为减少其他因素影响，不考虑流体的热物性参数变化。流动单元模型取11 mm×11 mm×2 mm 的两块长方体，换热单元模型取11 mm×11 mm×5 mm 的长方体。

图5 换热、流动单元模型

2.1.1 油冷器单元流动参数

本文中将油冷器单元的流动特性以多孔介质参数进行表征。早在1856年Darcy 就开展了多孔介质流动相关的研究，而多孔介质的模型最早是由Patankar 和Spalding［22］以分布阻力的形式运用到了换热器的流动计算中，此后使用多孔介质模型的数值研究工作发展迅速。多孔介质的压降特性主要用Darcy-Forchheimer 方程来描述，对于各向同性的多孔介质，可用式（1）来表达。

式中，S为动量方程源项；角标i代表笛卡尔坐标系的3 个方向；ρ为流体密度；L为多孔介质沿流动方向的长度（文中为单元模型流动方向长度）；C1为黏性阻力系数；μ为流体动力黏度；v为速度；Δp为流体流经多孔介质区域的压强差（文中为单元模型进出口压力差）；C2为惯性阻力系数。

由于油冷器内部冷、热侧翅片的布置相互交错90°，冷、热侧均存在流动低阻力方向和高阻力方向，因此需要将油冷器冷、热侧简化为各向异性的多孔介质，考虑各向异性的多孔介质方程如式（2）所示。

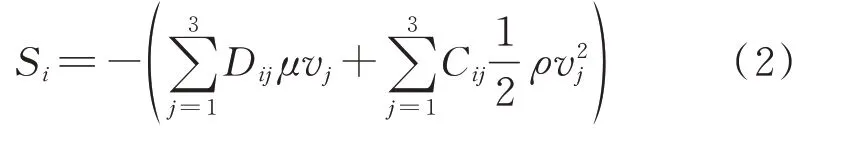
式中，角标j、角标i代表笛卡尔坐标系的3 个方向；Dij与Cij分别为黏性阻力系数C1对角矩阵与惯性阻力系数C2对角矩阵中的变量，以表征多孔介质不同方向的阻力特性。上述多孔介质参数均由具有实际几何结构的单元模型计算得到，不依赖于流动试验数据。

2.1.2 油冷器单元换热参数

使用dual cell 的冷、热侧网格之间虽然处于同一坐标位置上，但二者之间实际上不进行热量交换的计算，每一侧只计算本侧的流动与热扩散，所以需要以源项的形式来计算每一侧对流换热的热流量。在假设对流换热系数为平均值时，对于换热单元模型冷、热两侧，可写出如下公式：

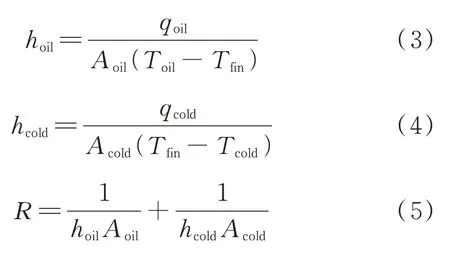
式中，hcold、hoil分别为换热单元模型冷侧、热侧平均对流传热系数；qcold、qoil分别为耦合计算得到的冷侧、热侧单元模型换热量；Acold、Aoil分别为单元模型中的冷、热侧换热面积；Toil、Tfin、Tcold分别为单元模型中热侧、翅片及冷侧计算域的体平均温度；R为忽略固体热阻的单元模型平均热阻。本文中油冷器因为其结构及实际工况，传热过程中导热热阻小于5.6×10-3，对流传热热阻大于1.0×10-1，相差两个数量级，可以忽略固体的导热热阻。上述对流传热系数由单元模型计算得到。由此可以得出冷、热侧对应的能量源项，如式（6）和式（7）所示。

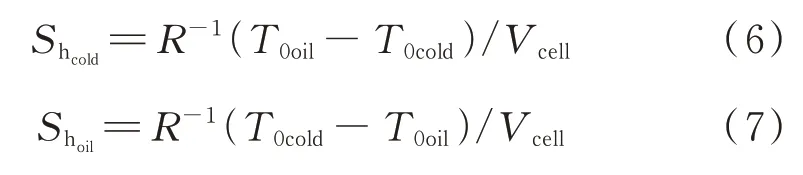
式中，Shcold、Shoil分别为冷、热侧能量源项；T0cold、T0oil分别为冷、热侧相同坐标位置的网格中心温度；Vcell为网格体积。

2.2 油冷器整体模型

使用dual cell 的油冷器整体模型如图6 所示，该模型不包含具体的流道结构与翅片结构。在翅片单元尺度内，将拥有流道、翅片详细结构换热单元模型等效为一个无具体结构的单元，如图7 所示。进行上述简化后，单元内部的流速不等同于实际流速，所以需要将简化单元内部的流速作为表观流速处理，单元的压降特性及换热特性均基于该表观流速进行表达。油冷器整体模型中，由于进出口油和冷却液的温度变化大，需要在整体模型中考虑流质物性参数的变化。

图6 油冷器网格示意图

图7 换热单元模型等效示意图

由于简化后的整体模型为包含冷、热侧计算域的两份网格，两份网格需要分别设置冷、热侧的多孔介质阻力特性参数。换热参数由式（3）和式（4）计算获得，整体的换热量由式（5）～式（7）计算获得（以用户自定义程序（user defined function，UDF）的形式），上述参数均由单元模型的模拟计算获取。

3 CFD 模拟

3.1 控制方程

本文中使用Fluent 19.0 的程序进行CFD 计算，通过连续性方程、动量方程及能量方程迭代求解获得换热单元详尽模型的流场与温度场。在计算流动与换热时为忽略流体变物性的影响，假设其为稳态流动，同时假设流体为不可压缩且物性参数为常数。

采用连续性方程如式（8）所示。流体为稳态流动且不可压缩，同时不考虑重力加速的影响，流体动量方程如式（9）所示。能量方程如式（11）所示。

式中，∇为哈密尔顿算子；v为速度矢量；∇p为压力梯度；为应力张量；I为单位张量；T为绝对温度；λ为导热系数；cp为流体的比定压热容；Sh为能量源项。ρ在不可压缩时为常数。

计算湍流时，采用Realizablek-ε模型，由于本文旨在讨论油冷器等效方法，此处不进行湍流模型的介绍。

3.2 流质热物性参数

本文中使用的机油为6 号传动油（ATF6），冷却液为50% 体积分数的乙二醇、水混合物，其物性参数使用拟合后的物性方程计算，如表1 所示。为了排除单元模型计算时物性对计算传热系数的影响，物性参数仅在换热器整体模型中参与计算。

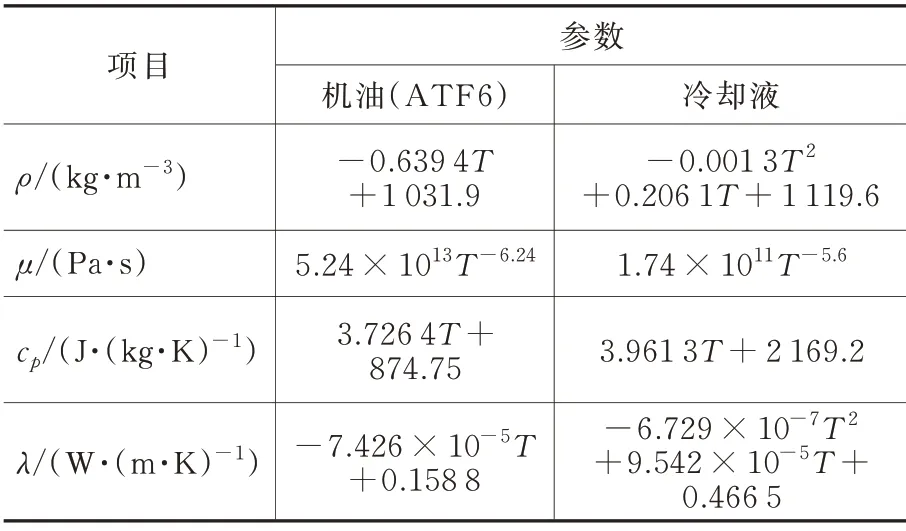
表1 流质物性拟合方程表

3.3 边界条件

计算冷、热侧介质在流道内的流动采用图5（b）形式的网格，进出口相应延长以避免进出口效应。经过网格无关性分析后认为网格为0.05 mm 时带来的单元温度变化误差可以接受，确定网格尺寸为0.05 mm。网格无关性分析如图8 所示。最终冷侧与热侧的网格数量均为4.0×106。固定冷侧流质的密度为1 018 kg/m3，热侧流质的密度为774 kg/m3，同时固定冷侧流质的黏度为8.25×10-4Pa·s，热侧流质的黏度为2.88×10-3Pa·s。设置入口边界为质量流量入口，出口为压力出口，壁面为无滑移条件，压力速度耦合使用Coupled 算法，为保证计算精度使用二阶迎风离散格式。

图8 网格无关性分析

计算冷、热侧流动换热特性采用图5（a）形式的网格，进出口同样相应延长，经过网格无关性分析后确定网格数量约为1.5×107个。此外，由于存在图2（b）所示的复杂流动，而图5（a）的网格形式只考虑了顺流、逆流、叉流的高低压侧流动换热，为了考虑流动与翅片呈一定角度时的换热情况，同时为了增加计算精度，添设一组每侧流动与翅片互成26.5°的网格模型（该角度由油冷器实际进出口位置决定，文中为进出口对角线与油冷器横边的夹角）如图9 所示。冷、热侧之间的夹角为53.0°，网格设置与上述一致，网格数量约为3×107个。与流动单元模型类似，计算换热时也不考虑流体的变物性，固定冷侧流质的密度为1 018 kg/m3，黏度为8.25×10-4Pa·s，比定压热容为3 615 J/（kg·K），导热系数为0.412 W/（m·K）；固定热侧流质的密度为774 kg/m3，黏度为2.88×10-3Pa·s，比定压热容为2 381 J/（kg·K），导热系数为0.129 W/（m·K）。设置入口为质量流量入口，热侧入口温度为130 ℃，冷侧入口温度为90 ℃，其余设置与流动单元模型边界条件设置一致。

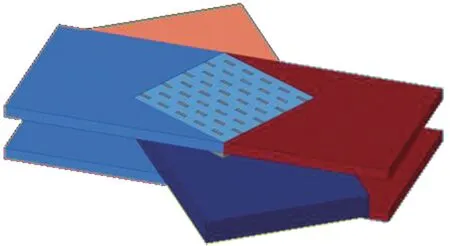
图9 冷、热侧夹角53.0°的模型网格

油冷器整体模型如图6 所示，其中将冷、热侧芯体部分设置为多孔介质，经过网格无关性分析，且考虑到计算效率，确定换热器整体模型的网格数量为6×105个。高温侧进口为质量入口边界，控制入口温度为130 ℃，低温侧进口也为质量入口边界，控制入口温度为90 ℃，高、低温侧出口均为压力出口，壁面设置为无滑移壁面，高、低温侧进出口段与芯体之间设置为interior 界面。压力速度耦合采用Coupled算法，使用二阶迎风格式以提高计算精度。

4 结果与讨论

4.1 热交换器单元模拟结果

4.1.1 单元流动结果

经过不同流量下流动单元模拟计算，得到冷、热侧高低压流向的阻力特性，如式（12）～式（15）所示。将这些特性曲线与式（1）及式（2）进行对比分析，可得到高低压流向的黏性阻力系数与惯性阻力系数，如表2 所示。

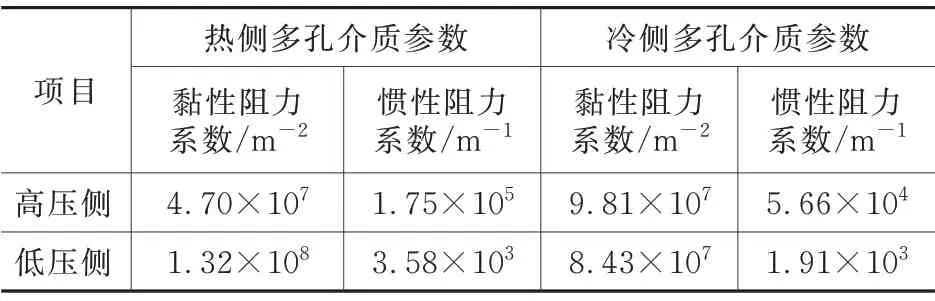
表2 多孔介质阻力特性参数

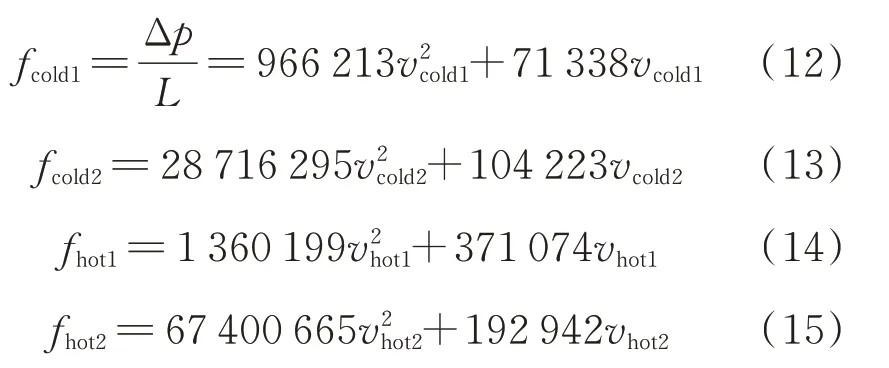
式中，fcold1、fcold2、fhot1、fhot2分别为冷侧低阻力方向、冷侧高阻力方向、热侧低阻力方向、热侧高阻力方向压降随速度的变化率；vcold1、vcold2、vhot1、vhot2分别为冷侧低阻力方向、冷侧高阻力方向、热侧低阻力方向、热侧高阻力方向的流动速度。

4.1.2 单元换热结果

经过不同流量和流动角度的传热单元模拟计算，得到冷热侧平均传热系数随流速和流动角度的变化数据，并以此进行曲面的拟合，结果如图10、图11 所示，拟合得到的对流传热系数关系式如式（16）、式（17）所示。

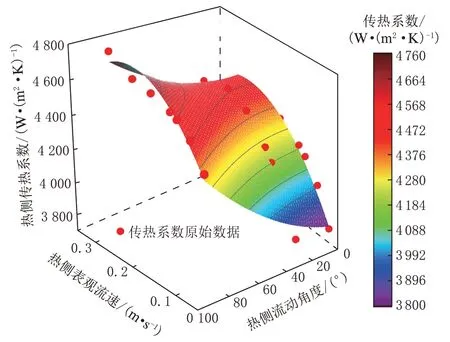
图10 热侧平均传热系数随表观流速、流动角度的变化

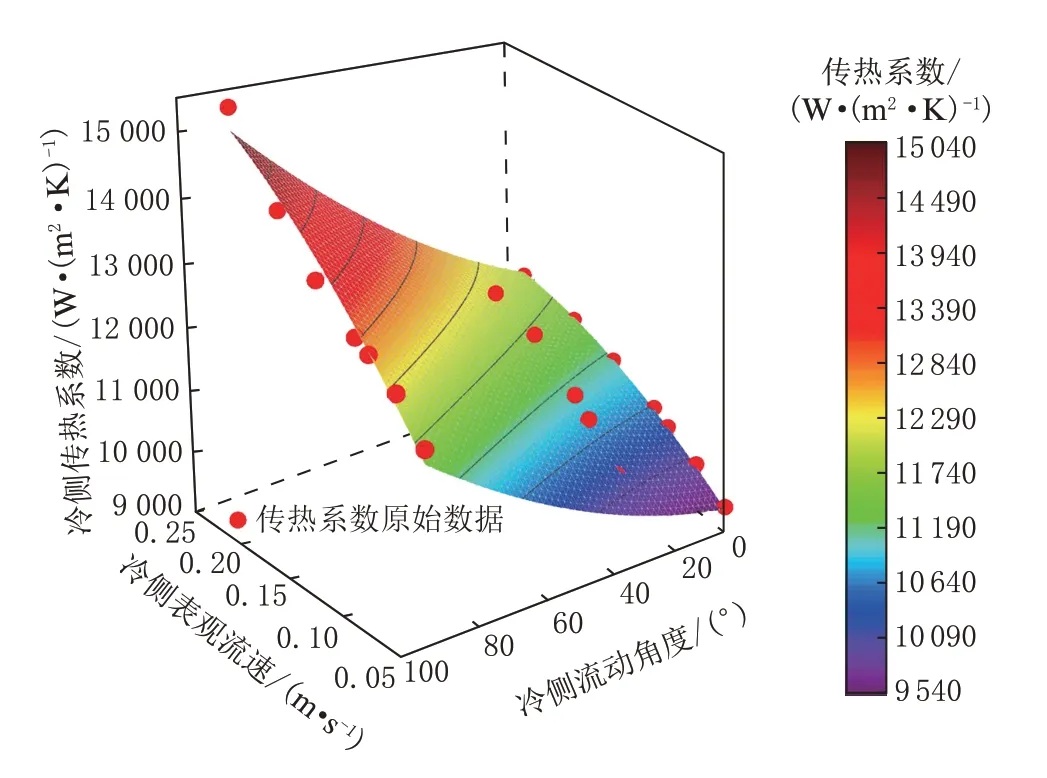
图11 冷侧平均传热系数随表观流速、流动角度的变化

式中，α、β分别为高温、低温侧流动与翅片之间的夹角，默认流动为低阻力方向时α、β均为0°。热侧与冷侧对流传热系数拟合曲面的R2值分别为0.97 与0.98。

4.2 油冷器等效流动结果

将计算得到的流动、传热参数分别以多孔介质参数及能量源项UDF 的形式代入等效模型，再根据油冷器出厂试验数据，选取相应工况进行换热器整体仿真，得到油冷器内部流动阻力特性及换热性能随冷、热侧流量变化的结果，冷侧流量变化范围为6.1 kg/min～15.2 kg/min，热侧流量变化范围为4.6 kg/min～12.2 kg/min。图12 为等效计算、试验及传统多孔介质模型计算在各工况下冷、热侧进出口压力差变化图（包含管路压损）。

图12 中，冷、热侧进出口压力差随着流量增加，且压力增加趋势也随着流量增加而上升，这也符合多孔介质的流动阻力特性。由图中数值可知，油侧压阻比水侧压阻大1 个数量级以上，这是因为油侧翅片布置方向垂直于流动方向，带来了较大的流动阻力。由于整体模型在管道处进行了相应简化，将带来部分计算误差，尤其在小流量工况中该误差所占比例较大。图中试验、等效方法及传统多孔介质模型在流动阻力上变化趋势相同，也说明了等效方法与传统多孔介质模型在预测流动阻力上的一致性，但是传统多孔介质模型在传热计算中仍存在较大误差。

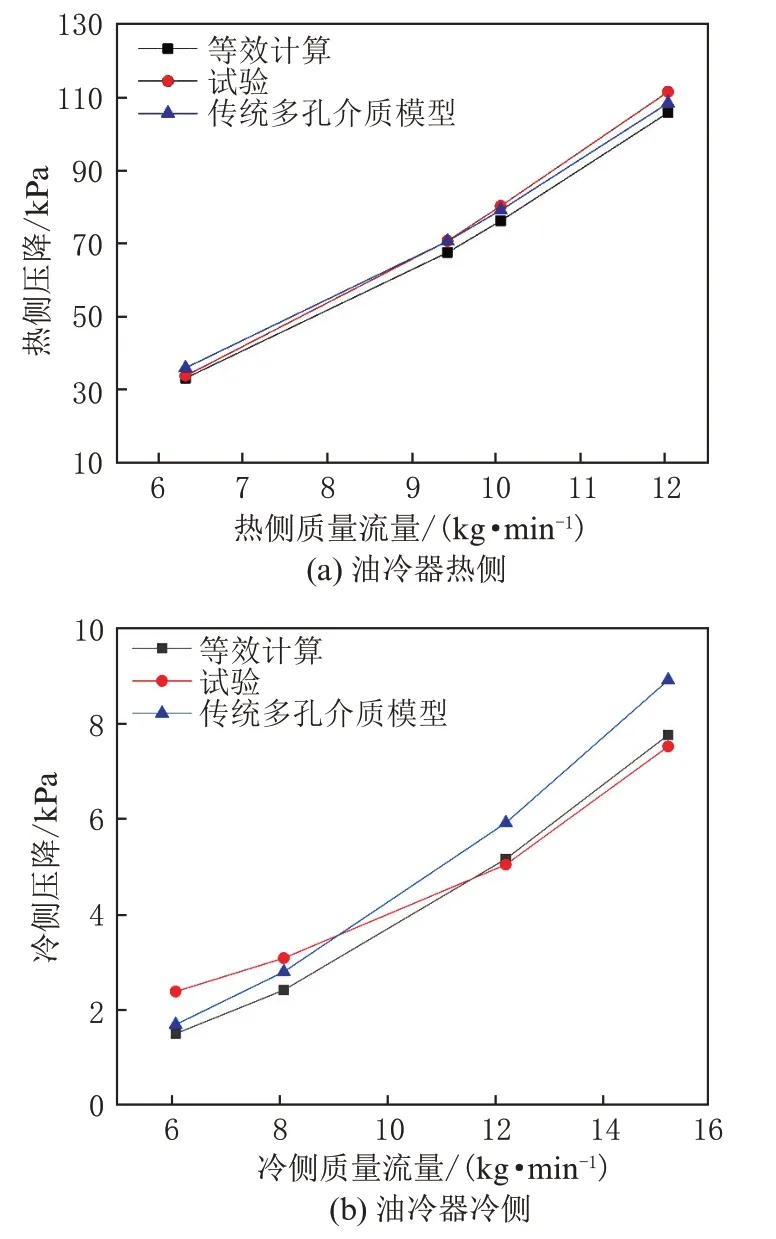
图12 油冷器冷、热侧压差随流量变化

4.3 油冷器等效换热结果

油冷器换热功率是换热器设计过程中重点关注的性能参数。图13 为不同流量下油冷器等效计算、试验及传统多孔介质模型计算的换热功率对比。从图13 中可以看出，等效计算方法下，换热器换热功率随流量的变化趋势与试验数据相一致，热侧流量在4.6 kg/min～11.6 kg/min 范围内模型计算精度较好，尤其是热侧流量为6.1 kg/min、9.2 kg/min时，等效计算误差分别约为4.4%、1.4%。此外该模型存在随热侧流量增加时计算误差先减小后增加的趋势。在冷侧流量为6.1 kg/min～15.2 kg/min、热侧流量为4.6 kg/min～11.6 kg/min 时等效计算的换热功率平均误差为3.5%；最大误差为10.8%，出现在冷、热侧流量最小的工况；最小误差为-0.3%，出现在冷侧流量为12.2 kg/min、热侧流量为9.2 kg/min的工况。而传统多孔介质模型在该范围内的平均误差为21.6%，仿真结果均大于试验值。该等效计算方法在换热误差上小于传统多孔介质模型。

由于换热器换热性能是由图10、图11 所示的拟合曲面决定的，而该拟合曲面在高速大角度时拟合曲面的值小于换热单元模型计算所得到的值，低速小角度时拟合曲面存在大于换热单元模型计算所得到的值，这与图13（a）和图13（d）所描述计算值与试验值的偏差相一致。由于拟合曲面存在失真情况，可能造成换热器等效计算时低流量、高流量与试验数据偏差较大的现象，为提高计算的精度，增加单元模拟工况点或是选择更贴合单元模型计算数据的拟合模型都将有助于提高整体模型的计算精度。

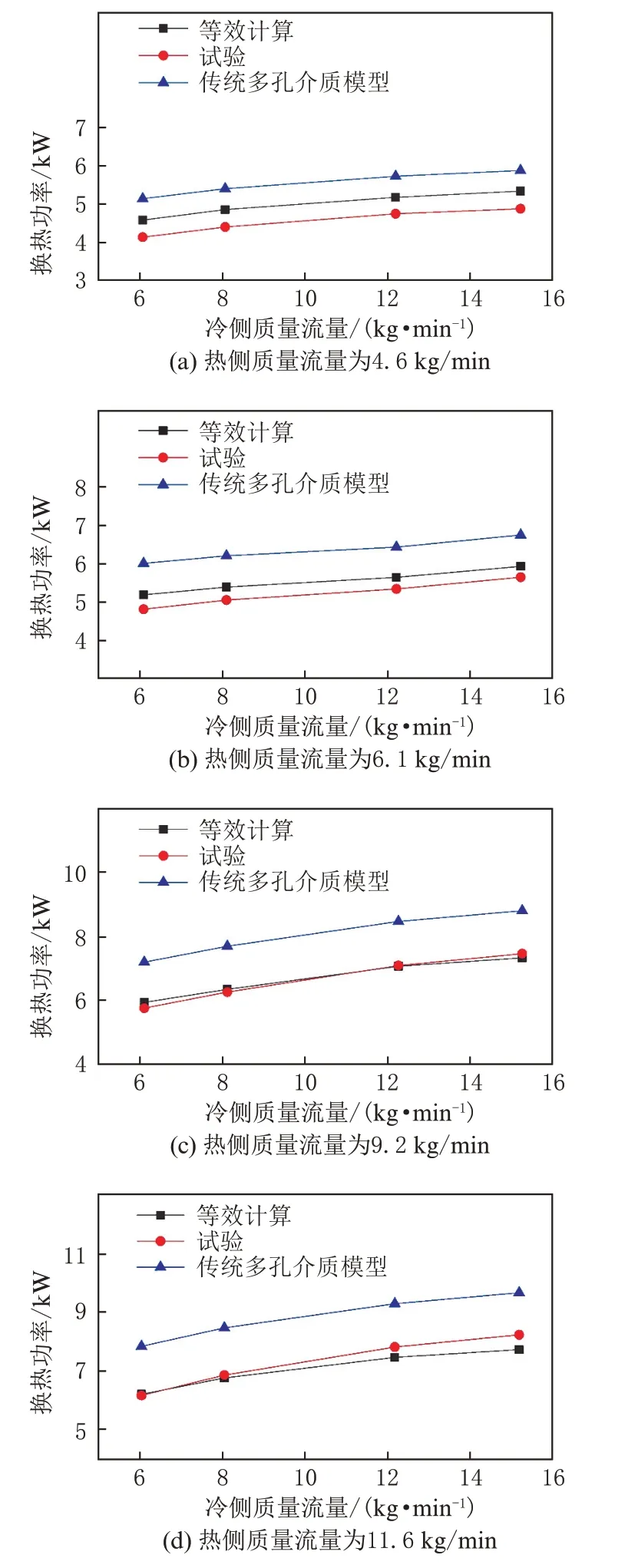
图13 不同质量流量下换热器换热功率变化

5 结论

（1）提出通过从流动单元模型和换热单元模型提取流动参数及换热参数进行换热器等效模型计算的方法，经过模拟计算与试验数据的对比证明了其有效性。该方法得到的流动阻力在中高速与试验数据符合程度良好，换热性能误差小于传统多孔介质模型计算结果。

（2）本文中计算方法对换热性能的计算误差受到对流换热曲面拟合的影响较大，为提升换热计算精度，可增加换热单元模型的工况数量或更换拟合曲面模型，以减小拟合曲面与换热数据工况点之间的误差。