混合动力货车能量管理策略硬件在环仿真研究

杜常清，杨贤诚，郭孔辉，何隽逸

（武汉理工大学 汽车工程学院，武汉 430070）

0 概述

重型商用车具有运输效率高且运输成本低的特点，成为各国长途运输的首选交通工具。中国中重载卡车的数量在总汽车保有量中占比并不高，但其消耗了60% 以上的公路运输能源，且中重载卡车的数量仍以年均70% 的增长速度飞速发展［1］。对中重型卡车进行合适的能量管理以提升经济性对节能减排及实现可持续发展有着重要意义。

混动卡车的能量管理策略主要分为基于规则的策略及基于优化的策略。基于规则的策略对整车控制器处理能力要求不高且开发成本低，鲁棒性好，能够广泛应用于各类需求；但是其对不同的工况适应性差，相关阈值参数的选定需要依据工程经验，无法实现混合动力系统的能量消耗最小化。基于优化的策略可分为实时优化和全局优化。全局优化算法中动态规划算法与庞特里亚金极小值原理是最具代表性的两种全局优化算法，这两种算法在已知工况信息的情况下能够得到理论最优控制序列，但计算量较大，无法实时应用在整车控制器中；实时优化策略中的等效油耗最小策略能计算出每一运算步中最优的发动机和电机的转矩分配，以此达到近似全局最优解，受到了广泛关注。

等效燃油消耗最小策略（equivalent consumption minimum strategy，ECMS）的关键是得到合适的等效因子，目前针对此策略的研究也多集中在等效因子的获取。文献［2］中首次将该策略应用于混合动力汽车能量管理中。文献［3］中首先通过理论确定等效因子的范围，然后运用射击算法确定了最优等效因子，取得了较好的控制效果。文献［4］中从动态规划（dynamic programming，DP）算法仿真结果中提取出最优等效因子，取得了较好的控制效果。文献［5］中针对四驱混合动力汽车设计基于ECMS 的能量管理策略，并用遗传算法优化等效因子和惩罚函数的参数提高了燃油经济性。文献［6］中利用粒子群算法优化特定工况下ECMS 策略中的发动机起动车速及等效因子，实现了不同初始电池组荷电状态（state of charge，SOC）条件下的近似全局优化。文献［7］中以插电式混合动力汽车为研究对象，指出等效因子作为电能消耗与燃油消耗的调控因素，受到初始SOC、行驶里程的影响，因此运用全局最优的遗传算法离线优化其在不同初始SOC 及里程下的等效因子，从而得到优化后的控制策略。文献［8］中将动态规划与ECMS 相结合，运用DP 的每一步的计算结果实时调整等效因子，以达到近似DP 的节油效率。

除了对特定工况下的等效因子进行研究之外，也有采用自适应实时调整的等效因子。文献［9］中提出了一种等效因子能随动力电池SOC 的改变而变化的ECMS 策略，利用多种工况对改进后策略的测试结果证明了其优于传统ECMS 策略的燃油经济性。文献［10］中提出了一种利用模糊比例积分控制器实现自适应调节等效因子的方法，可对等效因子进行实时调整。文献［11］中根据不同的SOC 初始值和预期里程，开发了自适应ECMS 策略。以上研究都是针对优化等效因子，未考虑到策略中对SOC 稳定性的控制，且部分文献中用作对比的规则策略较为简单。

针对这一现状，本研究中以燃油经济性及SOC偏离目标值程度之和为目标，通过Simulink 建立混动重载卡车纵向动力学模型，基于混合粒子群算法对某混动卡车ECMS 关键参数等效因子及惩罚因子进行优化，在满足动力性及SOC 平衡的条件下使等效油耗最小，并与基于DP 算法提取的规则的控制策略进行对比，在多个重型商用车标准循环工况下进行硬件在环测试，得出优化后的ECMS 策略能更好地提升燃油经济性的结论。

本文中针对ECMS 策略中等效因子的选取问题提出了基于粒子群算法（particle swarm optimization，PSO）优化的等效燃油消耗最小策略，并将其与用DP算法优化的规则控制策略进行对比，分析比较两种策略在相同工况下的燃油经济性并在实时硬件平台中验证策略的可靠性。验证结果证实了该策略具有实时性和瞬时性的特点，为开发高效的整车能量管理策略提供了参考依据。

1 混合动力系统建模

1.1 混动汽车结构及参数

本文中所使用的车型为P2 单轴并联式构型，结构示意图如图1 所示，图中D 为差速器。此构型中电机与发动机之间的动力传递通过离合器控制，通过离合器的结合与分离实现纯电模式、发动机模式及共同驱动等模式的切换。仿真车辆参数如表1 所示。

表1 车辆基本参数

图1 P2 构型混动汽车结构示意图

1.2 系统模型数学描述

1.2.1 发动机模型

本文中着重研究发动机的瞬态特性，故采用数据模型描述发动机。其中输出转矩采用一阶滞后响应，燃油消耗率be为转速ne及转矩Te的函数，即：

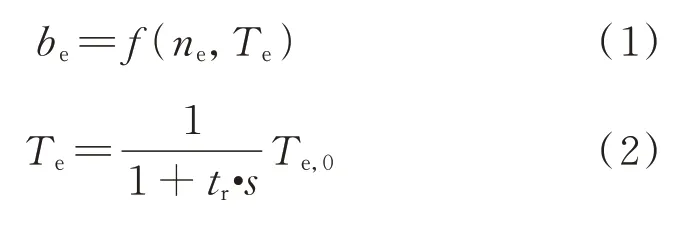
式中，tr为时间常数，取0.1 s；Te，0为发动机期望转矩；Te为发动机输出转矩；s为复变量。瞬时燃油消耗量可以由发动机稳态燃油消耗模型插值得到，发动机的最大转矩及最小转矩由不同转速查表获得。

1.2.2 电机模型

电机模型可以计算电机的输出转矩值和母线电流。在电机模型中，根据电动机的外特性和时间常数来模拟电机的转矩值；根据功率平衡和电机效率来计算电机的母线电流值Iin。电机模型的主要计算公式如式（3）～式（5）所示。

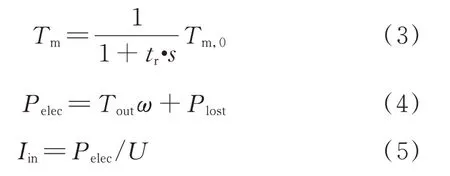
式中，tr为时间常数，取0.01 s；Tm，0为电机期望转矩；Tm为电机输出转矩；ω为电机转速；Plost为损失功率；Pelec为电机电功率；U为电池组两端电压。

1.2.3 电池模型

电池模型是一个复杂的非线性系统，本次建模忽略温升和电池寿命带来的影响，采用普遍选取的Rint 内阻模型进行搭建，主要公式见式（6）～式（8）。

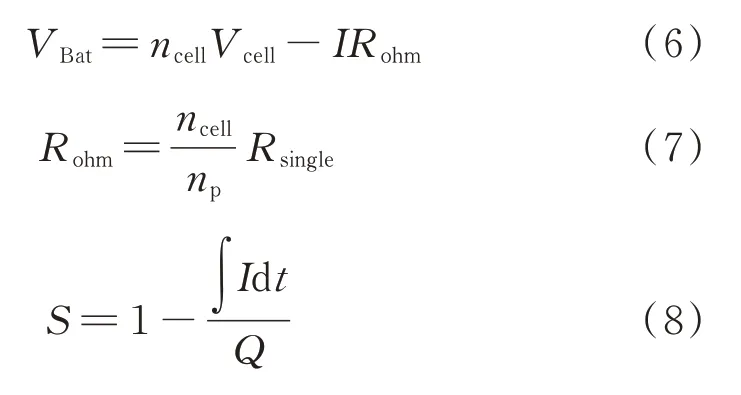
式中，VBat为电池组输出电压；ncell为一并电池的数量，取168；np为电池组并数，取2；Rohm为电池组总内阻值；Rsingle为数据查得单个电池内阻值；Vcell为单个电池电压；Q为电池组容量；I为电池组输出电流；S为电池组SOC。

1.2.4 车身纵向动力学模型

汽车的纵向动力学特性与整车的燃油经济性密切相关，不考虑车辆的横向动力学及垂向动力学特性，在忽略车轮发生滑动的情况下，制动力矩简化为作用于轮端的阻力矩。车辆在水平路面行驶过程中整车受到的阻力矩Tres的计算公式如式（9）所示。

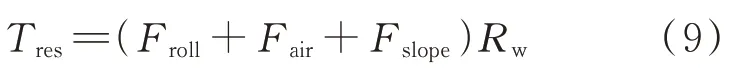
式中，Froll为滚动阻 力；Fair为空气阻力；Fslope为坡道阻力；Rw为轮胎半径。

2 实时优化的能量管理策略

2.1 等效燃油消耗最小策略

在众多的能量管理策略中，ECMS 是实时性较好且应用相对广泛的一种策略。其核心在于将车辆行驶过程中的电池电能消耗等效成燃油的消耗量，将某一时刻发动机的燃油消耗meng（t）与电池等效油耗mequ（t）相加即可得该时刻下整车油耗mfueltotal（t），如式（10）～式（12）所示。

式中，fp为惩罚函数［12］；可使车辆在工况测试中SOC尽量维持在一定范围；Starget为目标SOC 值；S(t)为t时刻SOC 值；kp为惩罚函数的惩罚因子；ηdis(t)和ηchg(t) 分别为电池放电及充电效率；P(t) 为电池功率，P＞0 为放电，P＜0 为充电；QL为所使用燃油低热值；λequ为充放电等效因子，对于充放电效率差异不大的电机，对应的λequ可取相同值［13］。

等效因子λequ与fp共同通过改变等效燃油消耗来影响系统的转矩分配决策。当S(t)＞Starget，此时fp＜1，则由式（10）可知，总等效油耗降低，系统决策倾向于电池组放电；当S(t)＜Starget，此时fp＞1，总等效油耗增加，系统决策倾向于为电池组充电；当S(t)=Starget，fp=1，系统决策不作调整。本文中目标SOC值设定为50%。最后根据式（10）～式（12）列出ECMS 算法的目标函数及约束条件，如式（13）所示。

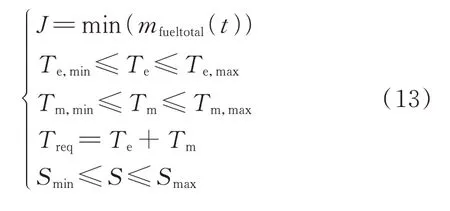
式中，Smin为SOC 下限值；Smax为SOC 上限值；Treq为需求转矩；J为最小油耗值；Te，min与Tm，min分别为发动机及电机的最小转矩；Te，max与Tm，max分别为发动机及电机最大转矩。ECMS 的关键参数为等效因子λequ及惩罚因子kp，故本文中利用PSO 算法寻找合适的取值以改善车辆行驶燃油经济性。

在该算法中，每一个计算步中首先由驾驶员模块得出车辆总的需求转矩，并将电机所需转矩按其最小及最大转矩值之间的范围均分为N等份进行预分配，余下的转矩由发动机提供。再对N+1 组转矩分配分别进行等效油耗计算，得出该步的总转矩需求下电机与发动机的最优转矩分配，如式（14）和式（15）所示。

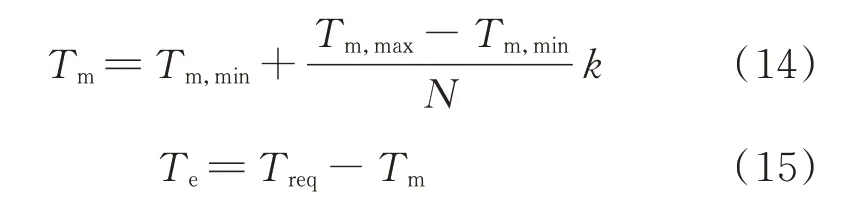
式中，k为正整数，取值为0～N。本文将电机转矩区间平均分为49 等份，即N=49，在一个计算步中得到50 组发动机与电机的转矩分配方案。

2.2 混合粒子群寻优算法

在众多群智能算法中，粒子群算法的特点是搜索速度快且易于实现，但也存在早熟收敛的问题。为此，采用改进惯性权重及加速系数来提高粒子群算法求解全局最优解的能力。

在该算法中，待优化变量为等效因子λequ及惩罚因子kp，在二维的搜索空间中将每个粒子的位置x和速度信息v定义为：

式中，i表示种群中第i个粒子；j为算法迭代次数，即种群中第i个粒子在第j次算法迭代中所表示的等效因子及惩罚因子的数值。在前j次迭代中，将第i个粒子个体的最优位置记为pi，将种群中最优位置记为gbest，故第j+1 次迭代中，粒子的位置与速度由式（18）和式（19）更新。

式中，w为惯性权重；c1及c2为加速因子；r1和r2均为［0，1］区间内的随机数。为防止PSO 算法的早熟收敛及在全局最优解附近产生的振荡现象，采用了线性惯性权重［14］，如式（20）所示。

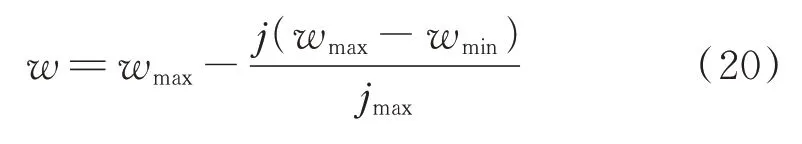
式中，j为迭代次数；jmax为设置的迭代次数的最大值；wmax为设置的惯性权重的最大值；wmin为惯性权重的最小值。加速因子由式（21）和式（22）计算。

式中，c1f、c2f、c1i和c2i为常量。

本文中为了兼顾不同SOC 终止值对评价发动机油耗结果的影响，设定PSO 算法的经济性目标函数为发动机燃油消耗量与终止SOC 偏离目标SOC的绝对值加权之和，如式（23）、式（24）所示。

式中，f为百公里油耗，∑mfuel(t)为一个工况结束后总等效油耗量；ρ为燃油密度；L为行驶距离；S为终止SOC 值；Starget为目标SOC 值；δ为权重因子。

基于上述公式，搭建模型并编写MATLAB 代码，基于PSO 的ECMS 控制参数优化求解流程结构如图2 所示。

图2 算法求解框架

3 仿真分析

3.1 PSO 算法参数寻优

为验证能量管理策略的可行性，本文中选取世界重型商用车瞬态循环（world transient vehicle cycle，WTVC）及中国重型商用车辆试验循环（China heavyduty test cycle，CHTC）进行仿真测试验证。

在MATLAB 中的.m 算法脚本文件里设置粒子群粒子总数为10，迭代40 次，线性惯性权重中wmax取0.9，wmin取0.5，加速因子cf与ci设定为0.9。

根据文献［15］可知，由发动机及电机效率可计算等效因子合适的取值范围并在此范围中搜索最优值，故设定待优化参数等效因子λequ的变化区间为［0，1］，惩罚因子kp的变化区间为［0，2］。

针对上述两种工况，惩罚因子与等效因子的优化过程如图3 所示。由图3 可知，惩罚因子及等效因子两个参数经过40 次迭代后基本收敛至最优解，得出优化后的等效因子、惩罚因子及由式（23）所求得的目标函数值如表2 所示。

表2 参数寻优结果

图3 惩罚因子与等效因子的寻优过程

3.2 基于规则的能量管理策略

为了验证所选取制定的ECMS 策略的实用性，针对上述两种工况使用动态规划算法得出理论全局转矩分配的最优值如图4 及图5 所示。

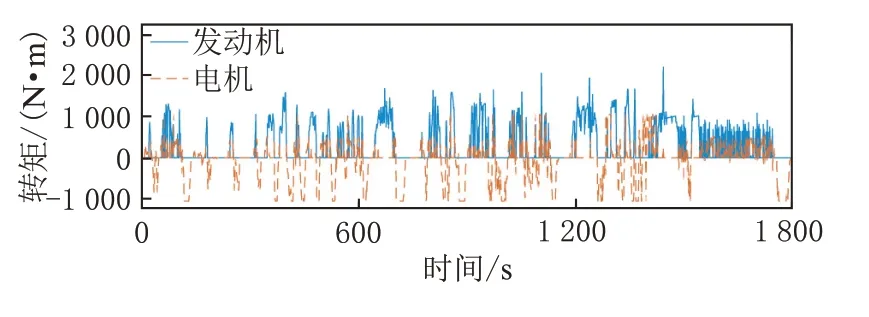
图4 WTVC 工况下基于DP 策略的发动机与电机转矩

图5 CHTC 工况下基于DP 策略的发动机与电机转矩

DP 算法能离线得到全局最优的控制效果，计算出在WTVC 及CHTC 工况下发动机理论最低油耗（百公里油耗，单位L/100 km，即10-2L/km）为19.06×10-2L/km 及18.59×10-2L/km。而由于其需要已知行驶工况并且计算量较大，无法应用于实时硬件在环测试平台，故依据DP 计算所得的发动机及电机工作点制定基于规则的能量管理策略，并与前文所制定的ECMS 策略在硬件在环实时平台中进行对比。

基于规则的控制策略模式切换主要依据发动机的最大转矩曲线、最优转矩曲线及最小转矩曲线划分工作区域，本文中依据DP 算法计算出的发动机及电机工作点，对不同驱动模式区域边界线进行拟合。分别拟合出两工况下新的发动机最大转矩曲线Tmax及最小转矩曲线Tmin如图6 及图7 所示，由此修改基于规则的控制策略。图6 和图7 中各变量定义如式（25）～式（28）所示。

图6 CHTC 工况下基于DP 算法的工作区域分布

图7 WTVC 工况下基于DP 算法的工作区域分布

式中，x为发动机转速；下标C 表示CHTC 工况下标W 表示WTVC 工况。

3.3 硬件在环仿真

在基于模型的设计（model based design，MBD）开发流程后期，通常使用硬件在环仿真（hardware in the loop simulation，HILS）进行测试验证，使用硬件在环实时平台可以使得系统仿真更加贴近真实的应用环境，同时对搭建的控制策略实时性及可靠性进行测试。

硬件在环测试部分使用dSPACE 公司下的SCALEXIO 与MicroAutoBox Ⅱ测试平台。其中SCALEXIO 机柜中具有可实现模拟执行器及接受各类传感器信号的板卡，可以在硬件在环测试中充当被控对象系统。MicroAutoBox Ⅱ是实时仿真系统的控制器板，其结合了快速控制原型和汽车电子控制器的优点，因此可以将控制策略模型嵌入至MicroAutoBox Ⅱ中，充当在环测试中的整车控制器。

通过控制器局域网络（controller area network，CAN）总线实现MicroAutoBox 和SCALEXIO 之间的通信，并由上位机实时观测仿真运行中车辆的状态信息，进一步对在环测试模型的完整性和正确性进行分析验证。在环测试验证平台的结构示意图如图8 所示。

图8 硬件在环测试结构

在策略模型与被控对象模型中配置好通讯模块后，将MicroAutoBox 与SCALEXIO 通 过CAN 总线连接实现数据通讯，并通过上位机ControlDesk 软件实时观测CAN 信号收发过程。

在仿真平台软件ControlDesk 中，一个周期WTVC 工况结束后，通过软件记录下所需状态参数的数据，并导出得到ECMS 策略下车速跟随图像如图9 所示，SOC 跟随曲线对比如图10 所示。

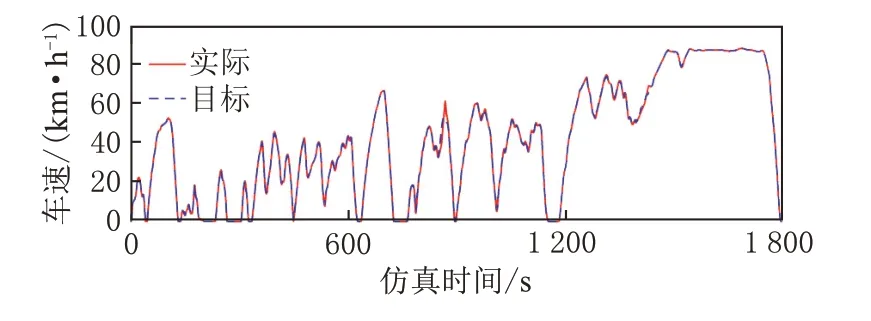
图9 WTVC 工况车速跟随情况

图10 WTVC 工况SOC 离线仿真值与在线测试值轨迹对比

根据图9 可知，实际车速与工况目标车速基本吻合，车速跟随误差较小。由图10 可知，在实时硬件平台中，工况终止时终了SOC 稳定在50.1%，验证了SOC 稳定策略在实时仿真中的有效性。离线仿真与在线仿真SOC 轨迹并没有完全重合，主要是因为在HIL 中使用实物线束进行数据通讯，相较于离线仿真，模型中数据的计算与传递具有一定的滞后性，但与离线仿真终止SOC 结果相差很小。由此可知，实时平台能实现ECMS 控制策略。

同时可观测到运行WTVC 工况过程中，动力传动系统发动机转矩、电机转矩及等效油耗数值如图11 所示。

图11 ECMS 策略各部件仿真结果

由图11 可知，在低转矩需求或电池组电量充足时，系统倾向于使车辆工作在电机驱动模式，如工况中刚开始的起步阶段；当转速继续升高后，发动机开始接替电机工作在高效区，如650 s 时刻左右行驶阶段；若需求转矩进一步上升，超过发动机在该转速下能提供的最大转矩阈值，则使车辆工作在混合驱动模式，如1 200 s 时刻左右的急加速阶段；急减速时，电机此时作为发电机，输出负转矩制动的同时为电池组进行充电。

通过该ECMS 策略对行驶过程中发动机转矩分配的调节，得出发动机的工作区域分布图如图12 所示。

图12 发动机工作点分布

由图12 可知，发动机较多工作在等功率最佳油耗区域，即图中椭圆圈区域，在此期间的工作时间占总工况运行时间百分比为28.37%，作为对比，基于DP 规则的策略发动机在该区域的工作时间占比为27.86%，说明优化后的策略能使动力系统更频繁地工作在高经济性区域。

为了验证所优化的策略具有较好的SOC 稳定性，取优化后的参数进行仿真测试，对WTVC 工况及CHTC 工况分别使用基于DP 优化的规则策略及ECMS 策略，得出SOC 变化轨迹如图13 及图14 所示。由图可知，在ECMS 策略中，通过惩罚函数对等效油耗的调节，其SOC 轨迹始终在一个范围内波动，并在一个工况结束后，SOC 能稳定在50% 左右，而基于规则的策略由于规则的约束，无法实时分配经济性最优转矩，但也可以使SOC 稳定在50% 附近。

图13 ECMS 策略下SOC 变化轨迹

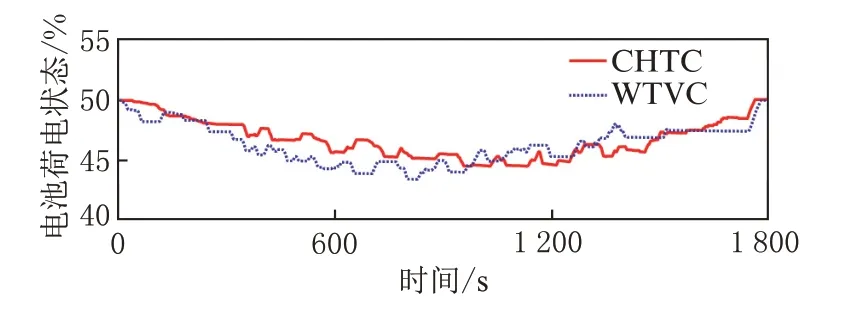
图14 DP 优化规则策略下SOC 变化轨迹

在工况前半段规则策略使电机主要工作在驱动模式，导致SOC 轨迹整体呈下降趋势。当SOC 处于较低水平后，电机在规则控制下更为频繁地工作在发电模式并对电池组进行充电，因此基于规则的控制策略SOC 轨迹波动较大。

两种策略下在两种工况结束后SOC 终值均为50% 附近，电池组电能变化很小，因而能衡量同一工况下，ECMS 策略相较于基于DP 的规则的控制策略对发动机实际油耗的影响。

针对WTVC 工况及CHTC 工况，测试发动机百公里油耗结果，并以上一节中DP 理论油耗最小值19.06×10-2L/km 及18.59×10-2L/km 为 基准，对比同一工况下不同策略与最小值的偏差百分比结果如表3 及图15 所示。

图15 发动机油耗对比

表3 不同控制策略燃油经济性对比

由图15 可知，本文中提出的基于粒子群算法通过离线优化得到最优ECMS 控制因子并应用到ECMS 实时控制策略中，能够合理地分配整车需求转矩，其偏差值比DP 规则策略更小；而由DP 优化的规则控制策略经济性略差于ECMS 策略。基于PSO-ECMS 能量管理策略兼顾了实时性与瞬时优化的优点，其能够应用到重型混合动力货车实时控制器中，为开发高效的能量管理策略提供了理论依据。

4 结论

（1）通过PSO 算法及设定合适的适应度函数对等效因子和惩罚因子进行离线寻优，该算法能较快收敛并获得WTVC 工况及CHTC 工况下对应的最优参数，实现等效油耗最小的控制策略。所使用的粒子群算法优化结果较依赖算法参数的设置，使用过程中应根据粒子搜索范围适当调整粒子搜索速度，搜索速度设置过大易丢失最优解，设置过小易使优化结果陷入局部最优，因此在相同算法参数下进行多次搜索，有助于验证优化结果的唯一性与可靠性。

（2）仿真验证结果表明，对本文中所提关键参数使用PSO 算法优化后，在WTVC 和CHTC 工况下，车辆等效油耗均有所下降，同时相较于传统的基于规则的控制策略，优化后的ECMS 策略的发动机油耗分别降低了3.63% 和1.36%，提升了燃油经济性。