长程视域：小学数学作业典型错例的迷思与矫正

沈 俊

（南京市江宁区秣陵中心小学，江苏 南京 211111）

在小学数学教学中，教师布置作业的目的通常有三：一是巩固知识技能；二是延续数学课程；三是补充评价方式。学生在完成作业的过程中，总会出现偏差或错失，其中具有代表性的错例可称为“典型错例”。对“典型错例”的研究，将有助于教师诊断学情，改善教学，从而提升自主执行数学课程的能力。

一、“典型错例”的迷思与溯源

学生数学作业中错题何其多，教师的迷思在于：那些“易错的”“总错的”的典型错例，不会随着时间的推移或教学对象的更替而“变得好一些”。这让我们在迷思中对“为什么总是错”追根溯源。

（一）知识与方法的缘由

学习者在知识结构或程序方法上有缺失和疏漏。这通常会被教师归结为“学生上课注意力不集中”“做题不细致不检查”，并因此苦口婆心地劝诫学生“上课好好听”“认真读题”等。比如：“4元买了5 支铅笔。每支铅笔多少元？1 元可以买几支铅笔？”如此浅白的一段话，学生自然读得通顺，但解答时却常常“翻车”，到底是“4÷5”还是“5÷4”？

有的教师“绝望”后，就会“套路”学生：“仔细看问题啊！问‘每支’就把5当作除数，问‘1 元（每元）就把4 当作除数’。记住了吧？”可是换了问题情境或描述形式后，学生还是不会。

这种方式不管用，是教师单方造成的。溯源学生“总是错”的缘由，是根植于教师心中的“效率论”，总想多快好省地把更多的知识与技能传授给学生，总想通过更多的作业进行巩固和熟练，学生却“无福消受”。

课程的参与度和学生的注意力等问题本质上是教师的问题，好的课程设计自然会吸引眼球。简单的纠错方法表面看起来有效率，却常常不为学生所接受与消化。

（二）心理与情感的因素

教师也常将错例的形成原因归结为“不喜欢数学”“没有良好的习惯”“没有挑战难题的决心和勇气”，即学生认识不到数学学科的价值，对数学学习缺乏应有的良好态度。其实，教育学首先是一种关系学，良好的教育发生在良好的师生关系上。小学阶段的学生尤其如此。正所谓“亲其师信其道”。

教师不能忽略典型错例形成的情感因素和心理机制。比如：作业中的规范意识，克服困难的勇气，自我调控的心理，培植耐心、细心和责任心等。为此，教师在设计矫正教学流程时，应充分考量学生的经验基础和心理机制，营造安全的错例分享氛围。譬如：作业对了不浮躁、错了不可耻、纠错了不起、倾听是好品质、分享自己的错更值得大力表彰等。如此，学生在矫正错例时，将由被动到主动，由消极到积极，其参与度与获得感会大大提升。教师可常常设计这样的矫正问题：说说你是怎么错的；他的方法错在哪里；他说的纠错方法好在哪里；还有更简洁的思路吗；你来出一道类似的题给大家做。

二、重塑“矫正方法”的认知与策略

认识到典型错例产生的原因，教师纠错时设计的矫正方法就不会短视，一味地追求效率，而是要奉行长期主义，葆有长程视域，把每一个错“点”联结成“线”，系统地看待错失与疏漏。这里的“长程视域”有三方面的意蕴：一是将点状断裂的错误进行系统分析，使其成为一个结构化的整体，并与学习者的经验有效对接；二是在实施矫正教学时，既重视补偿缺漏的知识技能，也要养育良好的数学学习情感；三是要拉长矫正时间。从错例的这个“点”散发开去，整体考量错例，即：怎样错的、为什么错、怎样纠错、这样矫正对后续学习有什么影响。下面，笔者试举一例，以说明长程考量矫正方法的意义与策略。

案例1：以“4 元买了5 支铅笔。每支铅笔多少元？1元可买几支铅笔？”为例。笔者任教的班级有46 名学生，首次练习此题共计有15 人混淆，不明白到底是“4÷5 还是5÷4”，错误率达三分之一，且平行班存有大量错误，历届学生皆会如此，此可谓“典型错例”。如何矫正？只有体认、观照到儿童学习难处，才有可能设计出针对性较强的矫正流程。

1.分析错误原因

一是难在读不懂。“4元买了5支铅笔”这句话文字上浅白易懂，但这个“懂”缺乏数学意义的支撑。读不懂则无法调用合适的经验来解决问题。

二是难在不好区分。五年级的学生在数学课堂里正式初始学习小数除法，原有的整数除法“大数÷小数”的经验会阻碍新知的迁移。何况把“4÷5”和“5÷4”混杂在一起，还要区分其不同的数学意义呢？

三是难在无法适时地进行心理调节。结论无法确认怎么办？随便写一个交差吗？学生尚不能自觉追问结果的逻辑自洽。

2.长程设计流程

环节（1）：达成基本理解。

师：你怎么理解“4元买了5支铅笔”？

生1：如果是“4 元买了4 支铅笔”，那么每支铅笔1元。这里“4元买了5支铅笔”，说明每支铅笔不到1元。

生2：也就是说1 元买一支铅笔，还要找零。1元可以买到一支多铅笔。

师：这两种方法至少能告诉我们是不是“算反了”。

生3：“4元”是总价，“5支”是数量，用“总价÷数量，4÷5”能算出单价“每支铅笔多少元”。反过来“5÷4”就是求“1元可买几支铅笔”。

师：能用前面学过的“数量关系”来解决新问题。真好！

生4：可以画图理解（如下，学生的阐释略去）。

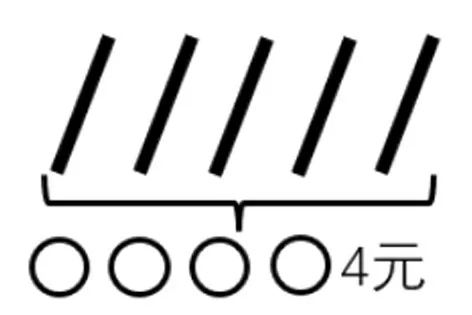
师：画图既能帮助我们直观地理解题意，也能从结果上看出是否符合题意。

环节（2）：呈现个性方法。

生5：老师，我受画图法的启发，想到一个简单的方法，永远不会错！（请他上黑板边画边讲解）先写出“4 元=5 支”，再把“4”移到右边来，就写成“5÷4”，算的就是1 元能买几支铅笔；如果把“5”移到左边去，就写成“4÷5”，算的就是1支铅笔多少元。

师：真有创意，很直观，此处应该有掌声！

环节⑶：学生模仿出题。

师：谁能模仿“4 元买了5 支铅笔”，出一道题给大家做？

生6：东东6分钟写了8个毛笔字。每分钟写几个毛笔字？写1个毛笔字要用几分钟？

生7：把2米长的绳子截成5段。可以提哪些问题？怎样解答？

……

分析上述案例，我们可以进一步明晰长程设计“典型错例”矫正方法的意义与策略。

（一）长程设计矫正方法的意义

叶澜教授认为，课堂教学要“将结构化后的以符号为主要载体的书本知识重新‘激活’，实现与三方面的沟通：书本知识与人类生活世界沟通，与学生经验世界、成长需要沟通，与发现、发展知识的人和历史沟通。用通俗的话来说，就是使知识恢复到鲜活的状态，与人的生命、生活重新息息相关，使它呈现出生命态。”［1］这就是一种长程视域，要将教学从“碎片化”转向“结构化”，从“知识态”转向“育人态”，从“效率化”转向“生命化”。

长程视域相对于急功近利的短视，具有课程视界和单元视角的整体性、系统性，教师要舍得在错误原因分析和矫正流程设计上花时间、下功夫，以期学生真正能从知识技能、思想方法、情感态度上获得新认知。

1.达成长程理解

学生将语言描述或文本呈现转化为数学意义上的理解，不是一件容易的事。此过程需要学生适当提取已有的经验，也需要在与同伴对话中获得启迪，更需要教师在思维“愤悱”处加以点拨。如上述案例中，学生能提取常见的数量关系“总价=单价×数量”，自然能理解“4÷5”和“5÷4”所蕴含的不同数学意义。推而广之，举一反三，这一类题都将得以解决。另外，学生画图“把4 从左边移到右边”“把5从右边移到左边”，既符合直观性的操作原则，易于学生理解“4÷5和5÷4”，也为理解分数意义“4/5和5/4”作了铺垫，同时也是方程移项方法的雏形。

2.积淀个性经验

课堂上有充分的时间展示、讨论和辩驳，师生均卷入其中，不再存有“局外人”，不同水平的学生将获得“属于自己的句子”，错误得以纠正，认知得以更新。这是一种“难教之法”——“难教之法”不是故作高深，刻意作难，而是指教师要探明学生的已有经验，理解其学习的“痛点”，精心设计教学流程和补偿策略，科学施教，精准干预。“教”应该尽可能走在“学”的前面［2］。如此，学生才会迷途知返，不再重蹈覆辙，积淀具有个体标签的错题矫正经验。

（二）长程设计矫正方法的策略

从上述案例中，我们可以得出有效矫正“典型错例”，教师要舍得投入时间与精力成本：一是单元备课时精心提前预判；二是有专属时间进行矫正。把原本较短的错题矫正时间，拓展成二十分钟甚至一节课，长程考量，保障矫正时间，科学施教，才有可能避免走进同一条犯错的河。为此，笔者建议在实施矫正课程时要找准时间节点，比如可每周安排一次，可在单元课程结束时安排，可在某个知识点诊断后安排，可根据需要适时灵活安排等。

根据个人教学实践，笔者初拟出矫正“典型错例”的基本流程与策略，以资批判与借鉴。

1.预判错误原因

教师至少在执行单元课程时，要对知识点进行梳理，对“重难点”“易错点”有预判，特别是对“典型错例”有详尽分析——可能错在哪里、会有几类错误、有哪些知识缺欠、经验的断裂点在哪里等。

2.引领课堂讨论

错题是重要的教学资源，化错为宝是为教学智慧。学生也只有理解错例的“然和所以然”后，才有可能避免二次犯错。所以，置身其中，身临其境，才能有所感悟。教师为此需要发挥引导者的作用，在愤悱处点拨，在迷失地指明，在关键点导引。

3.倡导直观分析

学生存在认知差异，不可能处于同一个水平上。这对大班额教学而言是一种挑战。但教学实验、教具演示、观摩实物、观看动画、画示意图、画线段图等直观分析方法有助于学生激活已有经验，走向认知的“最近发展区”。直观分析也有助于学生重构问题情境，促使发生精细加工。

4.学生自主出题

学习的发生通常是从观察和模仿开始的。学生自主出题基于学习者既有水平，且需调用合适的知识，又能激发想象力，是促使学习者集体参与课堂讨论的有效举措。学生自主出的题中，有的是“照搬”，有的是“高仿”，有的是“变异”，有的是“超越”，适合各种差异水平的学习者参与，丰富了题型题组，拓展了思考边界。

常使用上述矫正典型错例的基本流程与策略，将会促使师生逐渐形成一种认知图式。图式是将大量的信息组织进一个有意义的系统的结构，其有助于编码，因其给新学习的内容添加了细节。图式帮助我们产生和控制日常序列化的行动［3］。长期有计划地执行此流程与策略，便会形成一种范型和框架，其优势体现在：教学预设更周详，矫正时间有保障，教学方法更优化，讨论细节更丰富，学生参与更广泛。矫正课程因长程视域更具实效。

三、“典型错例”矫正分类举隅

为丰富“典型错例”的题型和矫正方法，以下再试举三例，以供一线教师在具体操作时参考。

（一）概念理解矫正：让隐性知识显性化

数学概念的特征是其表达的简约性和概括的抽象性。正是这种简约和抽象，遮蔽了前人实践探索的复杂性、过程性和丰富性，一句看似平白简短的描述，实则蕴含着诸多的数学意义。

学习完苏教版教材五上“圆”单元知识后，有作业形如：“请画一个半径2 厘米的半圆，并求出它的周长。”学生无可避免地要在“半圆”类的题型里纠缠不清。教师常常将学生的错误原因归结于“读题不清”，多要求学生圈划关键词“半径”“半圆”“周长”，如此，便可降低错误率。此不失为一种强化形式，但更科学有效的矫正方法是要有“长程视域”——错例的根本原因是什么？怎样矫正更有效？

环节1.教师出示“圆周长的一半，半圆的周长”。要求学生：读三遍，读通顺；数学上有什么不同？你有什么办法让大家都明白。

环节2.师生讨论。引导学生从语词上理解，比如：“圆周长的一半”是以一个圆周为研究对象，圆的周长已经存在了，它的一半“用圆周长除以2”就行；“半圆的周长”是以半圆为研究对象，所以需用“圆周长除以2 加直径”。如是，“画图法”呼之欲出。“画一画”既是增加操作细节，也是让隐性的思维显性化。如下图：

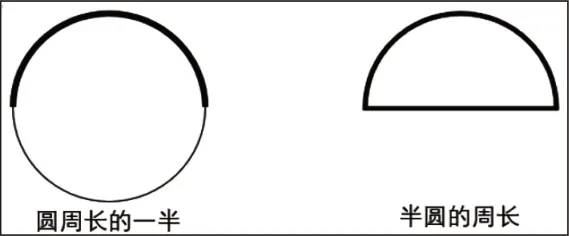
环节3.教师领着学生描一描，画一画，指一指，再给出数据，请学生计算。

环节4.呈现作业中的典型错例，主要有两类：一是计算含有半圆的组合图形的周长或面积；二是解决实际问题，如“靠墙围的半圆鸡圈”等。

环节5.每个学生出一道与“半圆”相关的题，与同学交流。

“圈划关键词”只是一种外在的强化手段，有一定效用，但尚需寻找错误的内在原因，从根本上理解概念。“圆周长的一半和半圆的周长”这句话读起来像拗口令，学生理解起来比较困难，容易混淆。其内在原因是对“周长”这一概念理解的缺漏。一个生活中的圆形物体或数学上的几何圆呈现在眼前时，人容易感知的是其面积大小，而非其一圈边线的长短。所以，学生很容易受到“面的一半”的负迁移，产生“线的一半”的错误结果。因此，需要在语词上初步理解后，通过画一画、描一描、指一指、说一说、算一算等具有数学意义的操作后，使隐性的关联显性化，才能真正为学生所理解。教师的作用是分析原因、设计流程、相机点拨，让学生在对话中纠偏、巩固、熟练。

（二）算法算理矫正：使操作序列化

《义务教育数学课程标准（2011 年版）》指出要发展学生的运算能力。运算能力主要是指能根据法则和运算律正确地进行运算的能力。培养运算能力有助于学生理解运算的算理，寻求合理简洁的运算途径解决问题。［4］于是，小学数学作业中常见的要求“下面各题，怎样算简便就怎样算”便成了学生计算时挥之不去的梦魇。譬如，苏教版教材五上“小数加法和减法”单元里的题目“12.45-3.6-2.45+4.4”，学生最常见的错例如下：

教师常用调侃的语气训诫学生“不能对简便计算上瘾”，却对错因缺乏系统分析。笔者认为至少对以下几个问题有了清晰认知后，才能较好地矫正错例，如：运算顺序是运算律的基础、同级运算可灵活应用交换律、读题分析优于直接计算等的欺骗性等。

为此，笔者设计了“朝三暮四猴吃桃”的故事情境，让学生在对话中自悟，举一反三。

师：听过“朝三暮四”的故事吗？有什么数学上的启发？

生：3+4=4+3；加法交换律a+b=b+a。

师：如果再添1个桃，你还能想到什么运算律？

生：加法结合律a+b+c=a+（b+c）；3+4+1=3+（4+1）；3+4+1=4+3+1；3+4+1=1+3+4；几个数相加，可以任意交换位置，把其中的两个数先加。

师：我们把故事再改一改：猴妈妈有10个桃，上午给小猴3 个桃，下午给小猴4 个桃，还剩几个桃？作为五年级的孩子，你有几种不同的方法解决这个问题？具体说一说其中的数学道理。

生：10-3-4=3；10-4-3=3；10-（3+4）=3；10-（4+3）=3。

师：五年级了，可不能这么“小儿科”，来点挑战，增加一个条件，比如——

生1：晚上又给小猴2 个，还剩多少个？可以列式：10-3-4-2；10-3-2-4；10-4-3-2；10-4-3-2；10-2-3-4；10-2-4-3。可以任意调换3 个减数的位置，差不变。

生2：也可以列式：10-（3+4+2）；10-（3+4）-2；10-3-（4+2）；10-3-（4+2）等很多不同的算式。灵活应用了“a-b-c=a-c-b=a-（b+c）”的运算性质。

师：再来改题：猴妈妈有10 个桃，上午给小猴3个桃，下午给小猴4个桃，晚上猴爸爸又采回来2个桃，现在猴妈妈有几个桃？挑战一下自己，看看你能写出多少个不同的综合算式。

生：略。

师：（呈现上述错例）下面我们再来看看这道题错在哪里？关于加减混合运算和“怎样算简便就怎样算”，你又有哪些新的收获？

学生讨论，教师相机点拨与小结，形成以下纠错算式：

……

经此“刻意训练”后，学生一般能形成这样的简便计算策略：先观察混合运算算式的特点，是否能运用相关的运算律或运算性质；再耐心地调整算式的顺序，一步一步用递等式计算；若有时间，可用其他方法进行检验。如此，才能正确、灵活地计算，形成计算能力。学生总结的经验，如“同级运算，先带着它前面的符号走”才显得鲜活生动，每个孩子都能在课堂里拥有自己的话语权，创造属于自己的学习故事。

（三）问题解决矫正：重新表征问题情境

如果当前状态和目标之间存在障碍，且这个障碍无法排除，问题便产生了。界定良好的问题通常有一个正确的答案，当调用某个流程或序列时，就能够找到答案。反之，解决问题的思路和方法短期内不明晰，就是一个界定不良问题。对于格式塔心理学家来说，问题解决是：（1）问题在人们的头脑中是如何表征的；（2）如何解决一个问题，包含对问题表征的重组和重构［5］。由此，对问题情境再加工与表征方式的重构，使结构不良问题转化为界定良好的问题，是正确解决问题的关键。

苏教版教材五下“因数和倍数”单元里的经典题型：“体操队训练，排成12人一队，缺4人；排成15人一队，还是缺4 人。这个体操队最少有多少人？”此题的主要错因有两点：一是无法达成数学意义上理解；二是不能正确调用相关知识。所以，教师可倡导学生使用画图、列举等方法，对问题情境重新表征，使之为学生可感知，可触摸，可理解。笔者设计教学流程如下：

环节1：读题。哪儿不太懂？请“懂”的学生说一说自己所理解的题意。

环节2：画图（如下左图）或列举（如下右图）。只考虑第一个条件“排成12 人一队，缺4 人”，可能会是多少人？再考虑第二个条件“排成15 人一队，缺4人”呢？

环节3：说理。“体操队最少有多少人”与什么知识有关？怎么办？

环节4：解答。［12，15］=60，60-4=56（人）。

环节5：检验。56÷12=4（队）……8（人）。这里的余的8人和缺的4人有什么关系？

环节6：拓展。如果不强调“最少有多少人”，你还能说出一种可能吗？

环节7：出题。出一道类似的题给自己做，次日分享。

如上述案例，教师有经验对典型错例进行预判，可将矫正流程前置，避免学习者陷入错误的泥淖。师生共同将抽象的文字通过画图、举例等方法重新表征，使问题结构由不良转为良好，各种问题解决的方案便水到渠成了。

“我都讲了N 遍了，学生怎么还错”——是的，即使教师再讲“N”遍，学生也还是会犯错，这是“典型错例”固有的样态。即：如果教师总是追求所谓的“效率”，就题讲题，就错论错，只是进行知识技能的复制搬移，不去思考知识产生背后的逻辑与意义，不去思考由此及彼的认知序列，那矫正教学就会流于表面，无法取得实效。但教师若葆有“长程视域”，遵循“矫正流程”——预判错误原因，引领课堂讨论，倡导直观分析，学生自主出题，把“错点”放大，将“短线”拉长，则有可能“连点成线”“化错为宝”，使矫正教学真正贴紧学生的经验，走进学生的思考，击中学生的灵魂。▲