基于重置温度方法的双参数介尺度气固传热模型构建

刘怡琳，李钰，余亚雄，黄哲庆，周强，2，3

（1 西安交通大学化学工程与技术学院，陕西 西安 710049； 2 新能源系统工程与装备陕西省高校工程研究中心，陕西 西安710049； 3 西安交通大学动力工程多相流国家重点实验室，陕西 西安 710049）

引 言

气固流化床反应器由于其良好的混合、传质和传热性能，在能源化工领域中得到了广泛应用，掌握气固两相流系统的流动和传热特性对于提高工业设备的性能具有重要意义。决定反应器动量传递及传热传质的关键参数为曳力、传热及传质系数。因此国内外有很多研究者针对上述系数开展了广泛的理论、实验及数值模拟研究，以获得上述系数的计算关联式。然而，现有研究中一些常用的关联式大都是针对于颗粒位置随机均匀分布的气固两相流系统[1]。气固两相在非线性相间曳力和固相应力的作用下，很容易产生非均匀的介尺度流动结构，如颗粒聚团等[2-3]。研究表明，计算中未考虑介尺度结构的影响会导致高估气固相间曳力、传热和传质[4-6]。

由于气固系统固有的复杂性，系统研究介尺度结构中气固传热现象的实验较少见诸于文献[7]。在过去的20 年中，计算流体动力学（computational fluid dynamics,CFD）已经成为模拟气固系统中流动和传热的越来越强大的工具[8]。在模拟中为了解析介尺度结构对流动及传热传质的影响，方法之一是采用足够小的计算网格（通常为数倍的颗粒直径）以满足近似均匀假设[9-10]，然而，对于大型工业反应器而言，细网格模拟的计算成本是无法承受的。因此在实际应用中，研究人员通常采用粗网格双流体法（two-fluid model, TFM）或多相质点网格方法(multi-phase particle-in-cell,MP-PIC)模拟大型流化床，但粗网格模拟无法解析介尺度结构的影响，即微尺度的近似均匀模型在有介尺度结构存在的粗网格模拟中不再适用，这就需要为适合工业尺度的粗网格模拟方法提供可以考虑亚网格非均匀性的介尺度模型，以得到合理的预测结果[11]。

目前，在不考虑传热的气固两相流研究中，研究者已揭示了构建介尺度曳力、介尺度应力等模型的必要性[12]，并基于能量最小多尺度方法（energyminimization multi-scale，EMMS）[13-15]、过滤方法[16-18]等开发了气固曳力介尺度模型。然而，对介尺度气固相间传热的研究还比较少。Dong 等[19]采用EMMS方法研究了介尺度结构对循环流化床提升管内气固传质的影响，他们发现，介尺度结构会极大地影响传质。Hou 等[20]使用EMMS 方法研究了快速流化床中非均匀流动结构与传递系数之间的关系。他们发现，介尺度结构对曳力系数、传质系数和传热系数有很大影响，他们指出，传统的均匀模型在有非均匀流动结构存在时不再适用。鲁波娜等[21]基于EMMS多尺度动量传递及传热模型对多产异构烷烃催化裂化反应器进行了模拟，研究表明，相比于传统的模型，采用多尺度模型可以更为准确预测反应器内的流动结构及温度分布。Shu 等[22]考虑了颗粒聚团结构对传热的影响，对传统传热系数模型进行了改进，采用改进的气固曳力模型及气固传热系数模型对下行床反应器进行了模拟，研究表明采用优化模型可以定性捕捉下行床的关键传热特性。Guo等[23]基于计算流体力学-离散单元法（computational fluid dynamics-discrete element method, CFD-DEM）研究了聚团在气固传热中的作用，他们定义了一个传热修正量来量化由聚团引起的局部不均匀性的影响，并提出了一个基于假定形状概率密度分布函数的统计模型。Lane 等[24-25]通过过滤双流体模型（TFM）的计算结果，开发了一个用于浸没水平圆柱体的气固两相流传热的亚网格模型。在他们的模型中，采用固含率、固相速度、圆柱体几何形状（直径和间距）和Peclet 数来封闭Nusselt 数。Rauchenzauner 等[26]提出了一个基于漂移温度的过滤相间传热模型。

Agrawal 等[27]构建了基于细网格TFM 模拟的过滤相间传热模型。他们指出，过滤后的介尺度相间传热系数比微观相间传热系数小1～2 个数量级，他们将微观相间传热系数的修正量（记为Q）建模为过滤固含率和过滤器尺寸的函数，在其模型中，过滤尺度小于等于16.7dp（dp为颗粒直径）时不再对传热系数进行修正（Q=0）。Huang 等[28]通过过滤细网格TFM模拟数据，将Q构建为过滤固含率、过滤器尺寸以及两相之间的无量纲过滤温差的函数，在其模型中，过滤尺度小于等于8.3dp时不再对传热系数进行修正（Q= 0）。Li 等[29]对Huang 等的模型进行了修正，取消了Q在（0,1）之间的限制。Lei等[30]通过过滤CFD-DEM 数据，构建了介尺度传热系数修正量与过滤固含率、过滤器尺寸及气固相间温差的函数关系。但Huang等[28]、Li等[29]模型中的无量纲过滤温差需要迭代获得，在实际的粗网格应用中存在困难，Lei 等[30]的模型对过滤温差的无量纲方法（除以0.0001 K 使得大部分的气固温差处于0～10 之间）缺乏普适性，同样导致模型应用困难。

另外，在现有的传热介尺度模型研究中，如何保持整个系统的热平衡是一个非常复杂的问题。为了保证气固两相间存在持续的相间温差，现有文献中使用了不同的方法。Rauchenzauer 等[26]在每个时间步让气相温度保持线性增加状态并在固相中设置热汇。Lane等[24-25]和Lei等[30]在固相中添加了热源项，热源项分别以1 K/s和0.1 K/s的速率加热气固系统。他们指出，加热速率的值是任意的，其大小不会影响模型结果。Agrawal 等[27]和Huang 等[28]在固相和气相中分别添加了热源和热汇项，他们也指出，所构建模型对所施加的热源热汇项的大小不敏感。以上方法可以实现气固相间温差的维持，然而如何维持气固相间温差以获得更符合真实物理过程（气固两相自由传热）的介尺度传热模型仍是一个问题。

针对以上问题，本文提出了一种重置温度的方法以维持气固温差，使得气固两相可自由换热，并基于细网格CFD-DEM 数据过滤获得了粗网格方便使用的介尺度气固相间传热系数修正模型。

1 细网格CFD-DEM 传热计算

CFD-DEM 方法是基于欧拉-拉格朗日坐标系的一种离散模拟方法，在欧拉坐标系下求解气相平均方程，在拉格朗日坐标系下求解颗粒方程，分别追踪单个颗粒的受力、运动及传热。有研究表明，CFD-DEM 采用小至1.75～3倍颗粒直径（1.75dp～3dp）的网格系统可以获得与解析到颗粒表面的直接数值模拟（particle resolved-direct numerical simulation,PR-DNS）近似的计算结果[31-32]。因此细网格（1.75dp～3dp）CFD-DEM 计算可以用来为粗网格计算提供非均匀介尺度封闭模型。本文的CFD-DEM 模拟通过对开源软件MFIX（版本19.2.2，https://mfix.netl.doe.gov/)进行二次开发实现，颗粒相和气相的动量、质量控制方程及求解过程可参考Garg 等[33]的研究。颗粒为典型的Geldart A 类颗粒，拟二维周期边界计算域垂直方向长度Ly为960dp，横向Lx为240dp，展向Lz为6dp，计算网格数量为384×96×2，对应x,y方向的网格尺寸为2.5dp。为了平衡周期域上的重力，在垂直方向上设置了恒定气体流量边界条件。整体固含率为0.05，初始时刻颗粒在计算域中随机均匀分布。为了保证气固两相间存在持续的相间温差，本文中选取了两种方法：方法一，参考文献中的方法给气相能量方程添加热源项，该热源项以0.1 K/s 的速度加热气体，该设定值的大小不影响计算结果[27-28]；方法二，每隔固定时间重置气体温度，所间隔时间为1为颗粒弛豫时间，单位为s，=18μg，其中，ρp为颗粒密度；dp为颗粒直径；μg为气相黏度），气固两相在1τstp内自由换热。在计算初始时，气相温度设置为1000 K，固相温度设置为0 K，气固两相间传热由能量方程控制，气相的能量方程如式(1)所示，具体可参考Lei 等[30]和Hou 等[34]的研究。

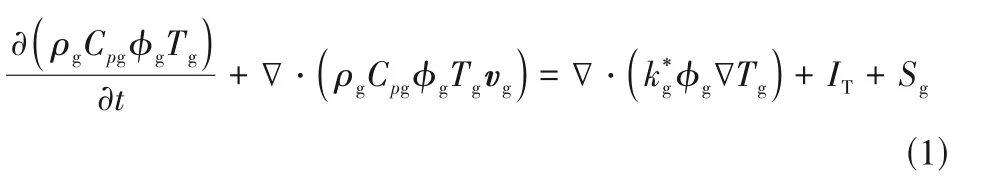
计算持续50τ，每0.2输出一次结果，计算后全场平均滑移速度、平均气固温差等统计数据达到稳定状态，即系统达到统计稳态[36-37]，后30τstp的数据用于模型构建。模型通过对计算结果进行过滤、拟合获得，所采用的空间过滤方法与Agrawal等[27]相同，具体可参考文献[9,27]，研究中所采用的过滤尺度为5dp、10dp、17.5dp、20dp、25dp和40dp。

表1 主要计算参数及设置Table 1 Parameters and settings

2 结果与讨论

与文献[27-29]中相同，本文针对介尺度传热系数修正量Q进行建模。Q定义为：

2.1 两种维持气固温差方法的讨论

为了便于表述，将方法一称为热源项方法，方法二称为重置温度方法。图1为两种温度设置方法下的固含率分布，即特定固含率对应的网格数量占总计算网格数量的百分比。可以看到，在本计算中，固含率在（0.025,0.03）范围内的网格数量较多，存在峰值，两种方法下固含率占比分布基本一致，流动结构基本一致，在此前提下开展两种维持气固温差的方法的对比和讨论是有效的。

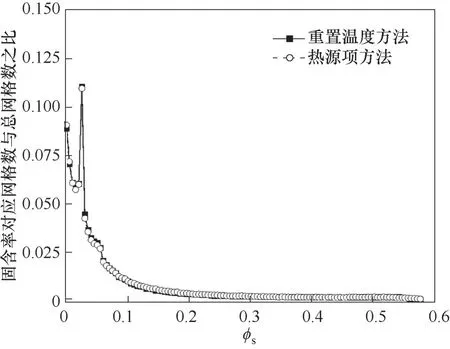
图1 两种方法下的固含率分布Fig.1 The distribution of solid volume fraction under two methods

图2为两种方法下计算域中平均气固温差随时间的变化，由图可知，两种方法均可以使得系统中存在一定的气固温差。方法一可以使得系统中气固温差在计算达到稳定后处于较为稳定的状态，波动幅度不大；方法二则是在每次重置气体温度后，气固温差逐渐下降，直至下一次重置气体温度。值得注意的是，两种方法得到的平均气固温差的绝对值不同，但在气固两相传热稳定后该温差的大小不影响Q的统计结果[27-28]。

图2 两种方法下计算域中平均气固温差随时间的变化Fig.2 The average gas-solid temperature difference in the calculation domain versus time under the two methods

为了对比两种方法对计算域内气固两相传热的影响，本文统计了不同局部固含率的传热量占计算域总传热量的百分比，以及局部单位体积传热量（某网格内的传热量除以网格体积）与总单位体积传热量（总传热量除以总体积）之比，如图3、图4 所示[为了凸显两种方法在大固含率下的区别，对纵坐标取对数，如图3(b)和图4(b)所示]。由图3 可知，两种方法下传热量占比均在0.025≤ϕs≤0.03 时存在峰值，即两种方法下占总网格数11.0%（图1）的固含率处于0.025≤ϕs≤0.03 的网格分别贡献了25.5%（重置温度方法）和18.65%（热源项方法）的传热量。由图4 可知，局部单位体积传热量与总单位体积传热量之比同样在0.025≤ϕs≤0.03时存在峰值，重置温度方法中该固含率范围内局部单位体积传热量是总单位体积传热量的2.32 倍，热源项方法中该固含率范围内局部单位体积传热量是总单位体积传热量的1.71 倍。重置温度方法在固含率较小时（ϕs< 0.03）局部单位体积传热量与总单位体积传热量之比大于热源项方法，而在固含率ϕs> 0.03 的范围内该比值小于热源项方法，二者差异在固含率大于0.1 时尤为明显。

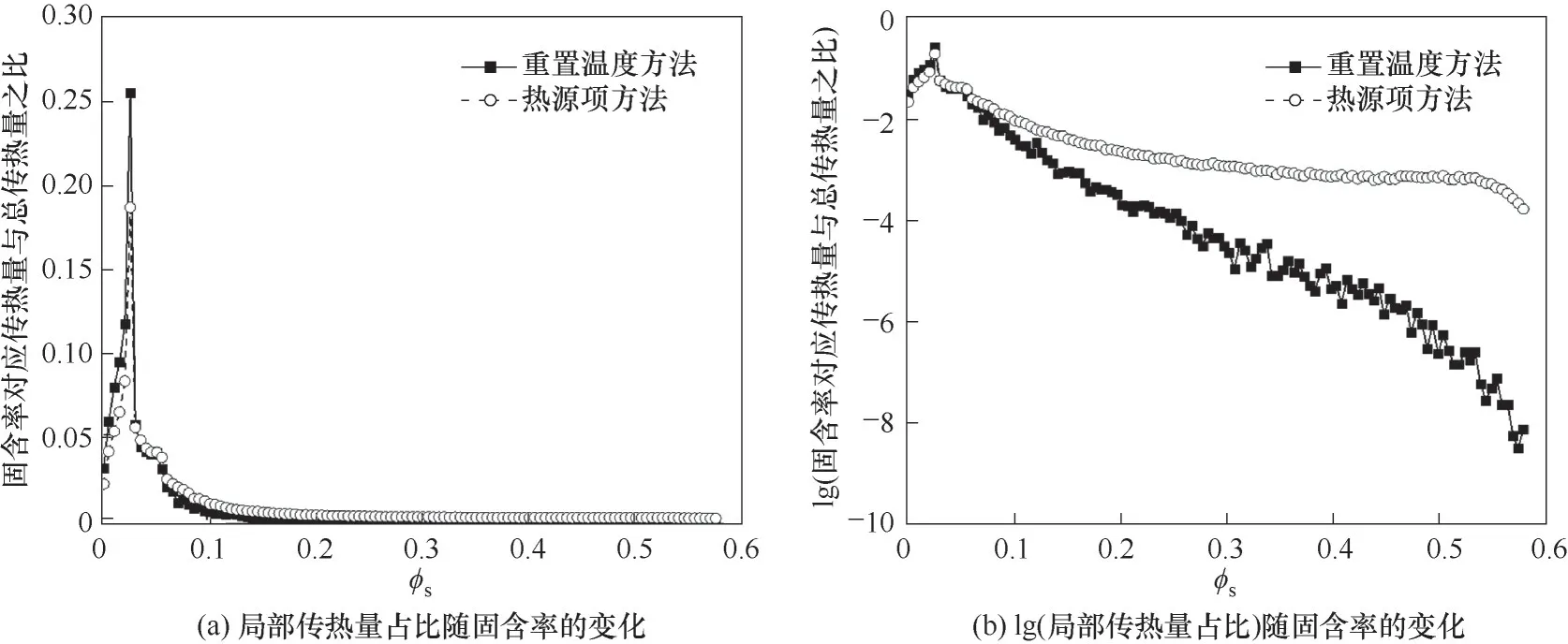
图3 计算域内总传热量在不同局部固含率下的分布Fig.3 The distribution of total heat transfer in the calculation domain under different local solid volume fraction

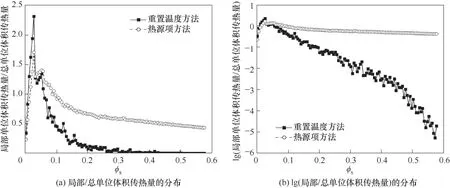
图4 局部单位体积传热量与总单位体积传热量之比Fig.4 The ratio of local gas-solid heat transfer per unit volume to the total gas-solid heat transfer per unit volume

为了分析0.025≤ϕs≤0.03 的特殊性，图5 展示了某时刻的颗粒位置图和固含率云图，可以看到0.025≤ϕs≤0.03（图5右侧图片绿色部分）的网格大多处于颗粒聚团边界位置，由此，下文将固含率范围为0.025≤ϕs≤0.03、ϕs<0.025和ϕs>0.03的区域分别称为界面、稀相和浓相区域。事实上，界面所对应固含率范围受整体固含率影响较大，本文整体固含率为0.05，所以界面所对应的固含率值较小。结合图3～图5 可以发现，两种方法均表明聚团界面位置的局部单位体积气固传热量与总单位体积传热量之比最大，重置温度方法在稀相和界面位置的局部单位体积传热量与总单位体积传热量之比大于热源项方法，而在浓相位置的局部单位体积传热量与总单位体积传热量之比小于热源项方法。为了更直观地了解本文所研究的系统中传热的分布情况，图6 统计了稀相、界面和浓相的网格数量占比（除去固含率为0的网格）及传热量占比，可以看到两种方法的固含率占比一致，而传热量占比却有所区别。两种方法的结果中，浓相、界面和稀相的网格占比分别为55.3%、11%和33.7%，而其对应的传热量占比却差别显著。在重置温度方法下，浓相、界面和稀相分别贡献了36.7%、25.5%和37.8%的传热量；热源项方法下，浓相、界面和稀相分别贡献了55.4%、18.6%和26.0%的传热量。总地来说，重置温度方法下稀相和界面的传热量占比高于热源项方法，而浓相的传热量占比则低于热源项方法。究其原因，热源项方法在气相中添加的热源（Sg）由式（3）计算：

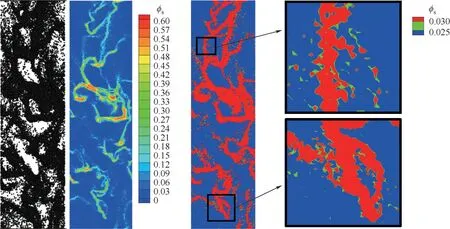
图5 某时刻颗粒位置及固含率分布Fig.5 Particle position and distribution of solid volume fraction at a certain time

图6 稀相、界面和浓相的网格数量占比及传热量占比Fig.6 The percentage of grid number and heat transfer of dilute phase,interface and dense phase

式中，Π̇为气相的能量输入速率，该设定值的大小不影响计算结果；ϕsd为计算域整体固含率；ϕgd为计算域整体气含率。由式（3）可知，气相所加热源项的大小与所在网格的气含率（ϕg）有关，不论网格内真实传热过程如何，均有热源加入促使其传热。当体系中存在化学反应时，热源项方法可能与实际较为吻合；当体系中不存在化学反应时，在浓相区域中气固相间传热一般会较快完成致使气固相间温差较小进而传热量减少，但热源项方法会强迫浓相区域保持一定的温差进而促进浓相区域的气固相间传热。重置温度方法保持了气固相间自由传热特性，仅通过反复重置温度获得足够的统计数据来完成建模。在无化学反应的气固传热系统中，气固两相间由于温差的存在会在能量方程控制下自发传热，该过程与本文所提出的重置温度方法所描述的物理过程类似，因此采用重置温度方法所构建的介尺度传热模型可能会具有较高的准确度。而在有化学反应的气固传热系统中，由于反应和流动、传热之间存在复杂的耦合关系，热源项方法所构建模型是否能较好地近似系统内的传热过程尚需更多的模拟或实验来进行分析和验证。

2.2 介尺度气固传热模型构建

图8 为两种方法在不同尺度下过滤得到的Q的平均值随过滤固含率的变化，两种方法下获得的Q有所不同，在固含率较大时，二者差异更为明显，整体上重置温度方法的Q大于热源项方法获得的Q。

基于图8 的数据，可将Q构建为过滤固含率和过滤尺度的函数，重置温度方法获得的模型拟合效果如图9所示，模型为：

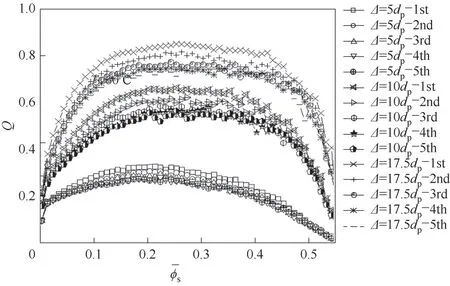
图7 重置温度后不同时刻的过滤Q随过滤固含率的变化Fig.7 The change of filtered Q with the filtered solid volume fraction at different time after resetting the temperature

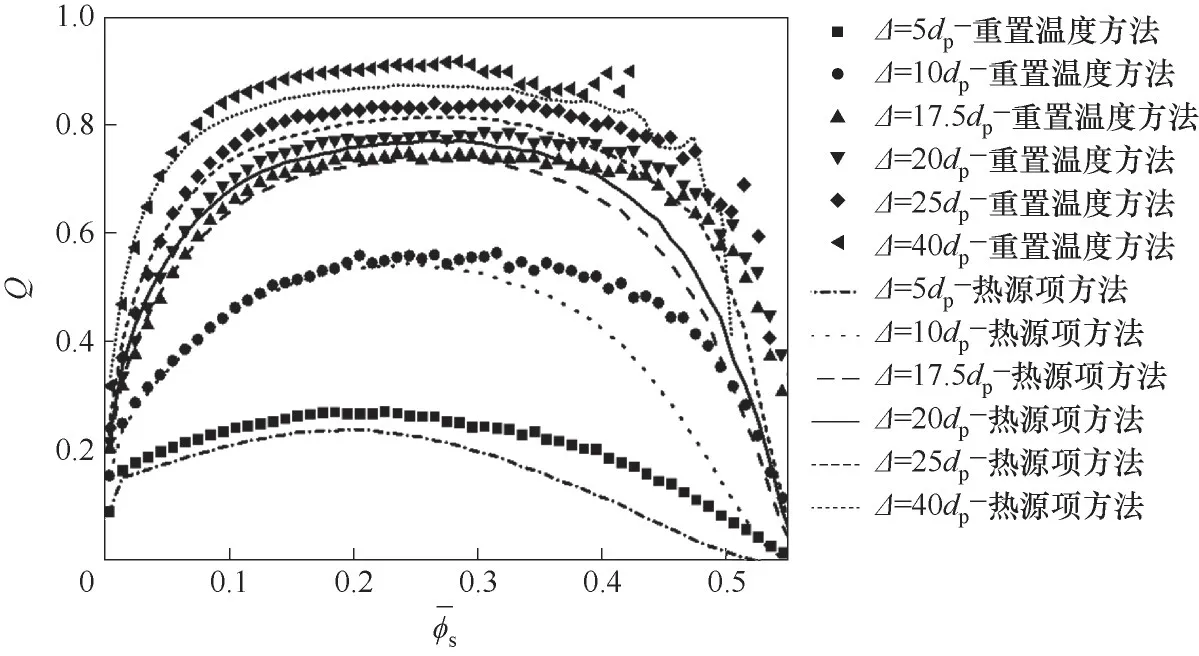
图8 两种方法在不同尺度下获得的Q的平均值随过滤固含率的变化Fig.8 The average value of Q obtained by the two methods varied with the filtered solid volume fraction at different filter sizes

图9 重置温度方法下介尺度模型拟合Q和真实Q随过滤固含率的变化Fig.9 The variation of fitting Q obtained by the mesoscale model and real Q with the filtered solid volume fraction under the resetting temperature method

值得注意的是，由图9 可知，当过滤尺度较大时，如为25dp及40dp时，过滤固含率的最大值小于小过滤尺度的最大值。造成此现象的原因为计算区域有限（240dp× 960dp），过滤尺度为40dp时已占据了横向尺寸的1/6，很难出现粗网格上的高固含率。加之全场整体固含率为0.05，随着过滤尺度的增大，粗网格内的固含率会逐渐接近整体固含率。

2.3 介尺度气固传热模型先验分析

本节将对上述模型进行先验分析，评价指标采用Pearson相关系数[36]，其计算式为：

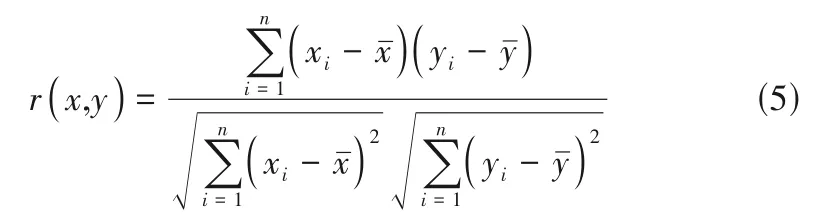
式中，x、y分别为模型预测值（Qpredict）的数据集和粗网格过滤值（Qexact）的数据集；xˉ、yˉ分别为数据集的平均值。采用本文所构建的模型[式(4)]对不同过滤尺度和固含率下的Q进行预测，预测值（Qpredict）与基于细网格CFD-DEM 模拟的粗网格过滤值（Qexact）的Pearson 相关系数如图10 所示，本文所构建模型的表现明显优于Agrawal 等[27]的模型，而且随着过滤尺度的增大模型表现在持续变好。这是因为本文的模型是基于细网格CFD-DEM（网格尺寸为2.5dp）的模拟数据，而Agrawal 等[27]的细网格模拟采用的网格尺寸为16.67dp，所构建的模型是基于至少2 倍的基础网格即33.34dp的数据，因此理论上模型适用范围为过滤尺度大于等于33.34dp，因此导致其模型在小过滤尺度时表现不如本文所构建的模型。更重要的是，采用网格大小为16.67dp的模拟数据作为建模数据，本身已完全忽略了比16.67dp尺度更小的非均匀结构对更大尺度上流动和传热的影响，因此所构建模型准确度较低。事实上，大量研究表明，对气固两相流动进行完全解析需要在3dp左右的网格尺寸[38-39]。另外，与文献中所采用的热源项方法不同，本文所构建的模型基于重置温度方法，数据源的不同也是导致模型表现不同的原因之一。最后，相较于TFM，CFDDEM 可以追踪颗粒的运动，计算得到的介尺度结构更为准确。图11 为所构建模型在不同过滤尺度下模型预测值（Qpredict）与粗网格过滤值（Qexact）相对误差的概率密度分布。可以看到随着过滤尺度的增大，相对误差逐渐向0 集中，即在模型应用中，在本文所研究的网格尺寸范围内，所采用的粗网格尺寸越大，模型的表现越好。本文所构建的模型可适用于过滤尺度小于等于40dp时的粗网格气固传热计算。另外需要指出的是，本文所构建的模型是基于周期性边界的模拟数据，未考虑壁面效应，在实际应用过程中，若壁面剪切效应较强，则可能会存在误差。

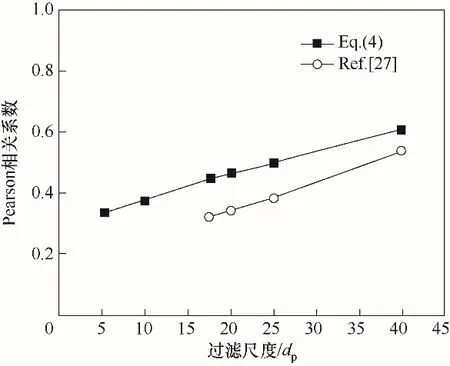
图10 不同过滤尺度下模型预测值（Qpredict）与粗网格过滤值（Qexact）的Pearson相关系数Fig.10 Pearson correlation coefficients between Qpredict and Qexact under different filter sizes

图11 不同过滤尺度下模型预测值（Qpredict）与粗网格过滤值（Qexact）相对误差的概率密度分布Fig.11 The probability density distribution（PDF）of relative errors between Qpredict and Qexact at different filter sizes

3 结 论

本文采用CFD-DEM 研究了气固两相流相间传热问题，比较了两种维持气固相间传热温差的方法的优缺点。方法一中给气相能量方程添加了热源项；方法二中每间隔一段时间进行气相温度重置，重置后气固两相进行自由传热。基于重置温度方法的过滤数据构建了适用于粗网格计算的气固相间介尺度传热模型，先验分析表明所构建模型具有优越性。具体结论如下。

（1）聚团界面位置的局部单位体积气固传热量占比最大，重置温度方法在稀相和界面位置的局部单位体积传热量与总单位体积传热量之比大于热源项方法，而在浓相位置该比值小于热源项方法。分析表明重置温度方法更适合计算气固相间自由传热的情况。

（2）基于过滤固含率和过滤尺度构建了介尺度气固相间传热系数修正因子的封闭模型，所构建模型的Pearson相关系数随过滤尺度的增大而增大，所构建模型预测得到的Q与真实Q的Pearson 相关系数高于文献中已有的双参数模型，模型适用于粗网格尺度小于等于40 倍颗粒直径的气固两相流传热计算。

由于介尺度传热模型的后验十分复杂，涉及介尺度曳力模型的选择与验证，目前文献中尚未有介尺度传热模型的后验报道。后续将继续探索介尺度传热模型的后验方法，开展相关的后验研究，以进一步评估所构建介尺度传热模型在实际应用中的表现。