小球沿竖直圆轨道运动脱轨后问题的探讨

董廷灿

(安徽省明光中学，安徽 滁州 239400)

1 问题的呈现

如图1所示，半径为R的光滑圆形轨道置于竖直平面内，并固定在光滑的水平面上，质量为m的小球(可看成质点)从最低点A以初速度v0开始运动(忽略空气阻力)。若小球脱轨：(1) 脱轨的位置如何确定？(2) 脱轨后小球将做何种运动？轨迹如何确定？

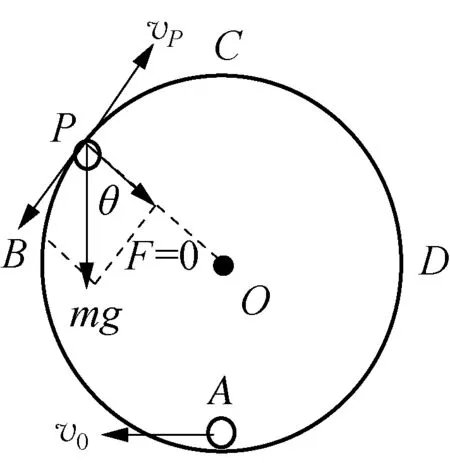
图1

2 问题的解决

2.1 脱轨位置的确定

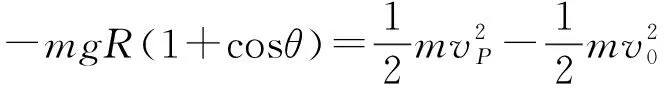
下面就极端情况对结果进行讨论：

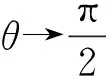
2.2 小球脱轨后的运动性质及轨迹的确定

从轨道上P点脱轨后，小球将以速度vP做斜抛运动。如图2所示，以轨道的圆心为坐标原点，水平向右为x轴正方向、竖直向上为y轴正方向建立平面直角坐标系，则P点的坐标值为：xP=-Rsinθ，yP=Rcosθ。

图2

把P点的速度vP分解为水平分速度vPx=vPcosθ，和竖直分速度vPy=vPsinθ，则在水平和在竖直方向上分别有：vPx=vPcosθ，x-xP=vxt=vPtcosθ④

2.2.1 小球到达最高点的位置

联立③、⑦两式解得：

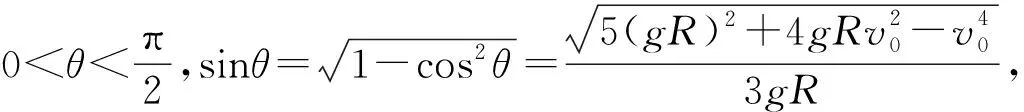
2.2.2 小球落到圆轨道上的位置

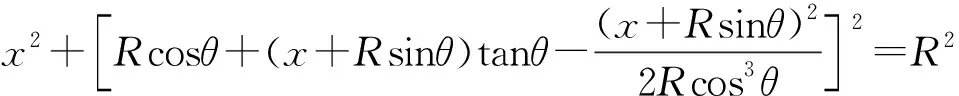
解出x的坐标值后，再代入⑥式即可求得y的坐标值，从而得到从不同θ所对应的P点脱轨后打到圆形轨道上的位置坐标，下面对打在圆轨道上的几个特殊位置进行讨论。

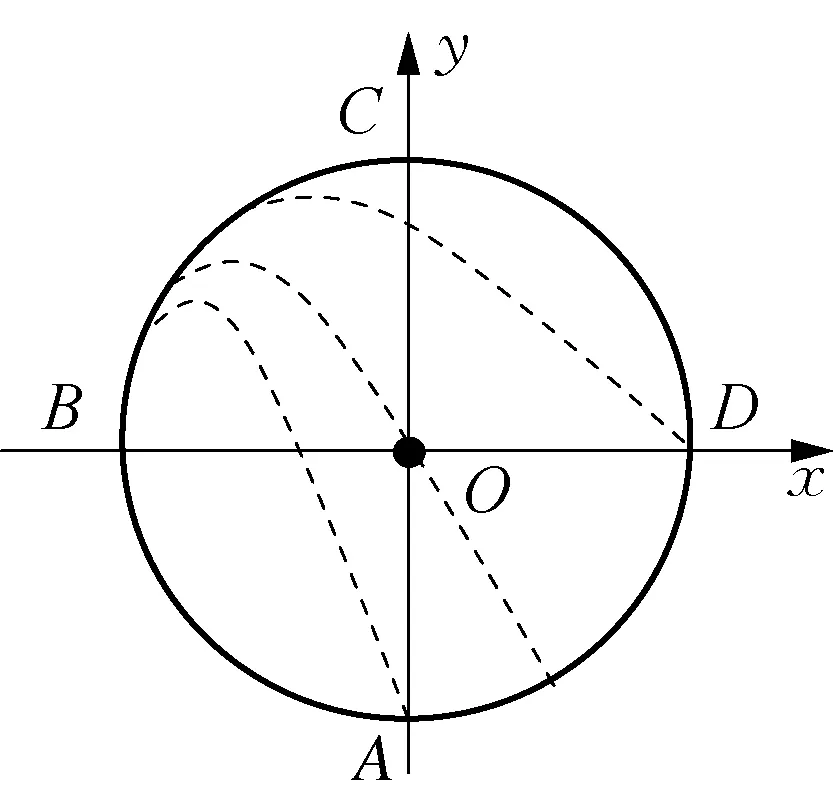
图3

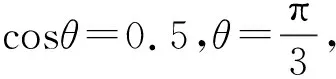
对于脱轨后到打到轨道上所用的时间文献[2]已做探讨，这里不再作分析。