促进深度学习 提升核心素养①
——由一道中考物理题引发的思考
徐 杰 张俊辉
(1. 江苏省苏州学府中学校,江苏 苏州 215008; 2. 江苏省苏州市高新区第一初级中学校,江苏 苏州 215011)
1 问题的提出
深度学习是一种基于理解的学习,是指学习者以高阶思维发展和实际问题的解决为目标,以整合的知识为内容,积极主动地、批判性地学习新的知识和方法,并将它们融入原有的认知结构,且能将已有的知识迁移到新的情境中的一种学习。[1]随着我国课程改革的推进,中学教学聚焦于学生核心素养的发展,在此背景下,深度学习得到普遍关注和推行。在深度学习理念下教师需要引导学生积极主动地掌握学科核心知识和思想方法,优化认知结构,并能在新的情境中迁移应用所学知识。深度学习可以激发学生高投入的学习状态,完善认知结构,提升高阶的综合能力。中考复习承载着学生知识结构化、新情境的问题解决、高阶思维发展及核心素养提升的任务。因此,将深度学习理念与中考物理复习教学实践相结合是值得研究的问题。
复习课如何上?是很多一线教师关注的话题,是不是通过一本复习资料,让学生按部就班地做题,或是把之前的知识进行罗列,亦或把原有的实验再做一遍?显然这些做法在倡导核心素养发展的今天都是不合时宜的。如何在初三中考一轮复习时进行有效的复习,促进学生的深度学习,从而提升学生的核心素养?笔者以“密度实验复习”为例,与同行交流。
2 中考物理题赏析
例1(2020年无锡):如图1所示,小红利用托盘天平(最大测量值为200 g,分度值为0.2 g)、量筒、水(ρ水=1.0×103kg/m3)、食盐、烧杯、白纸、滴管、勺子等器材配置盐水,步骤如下:
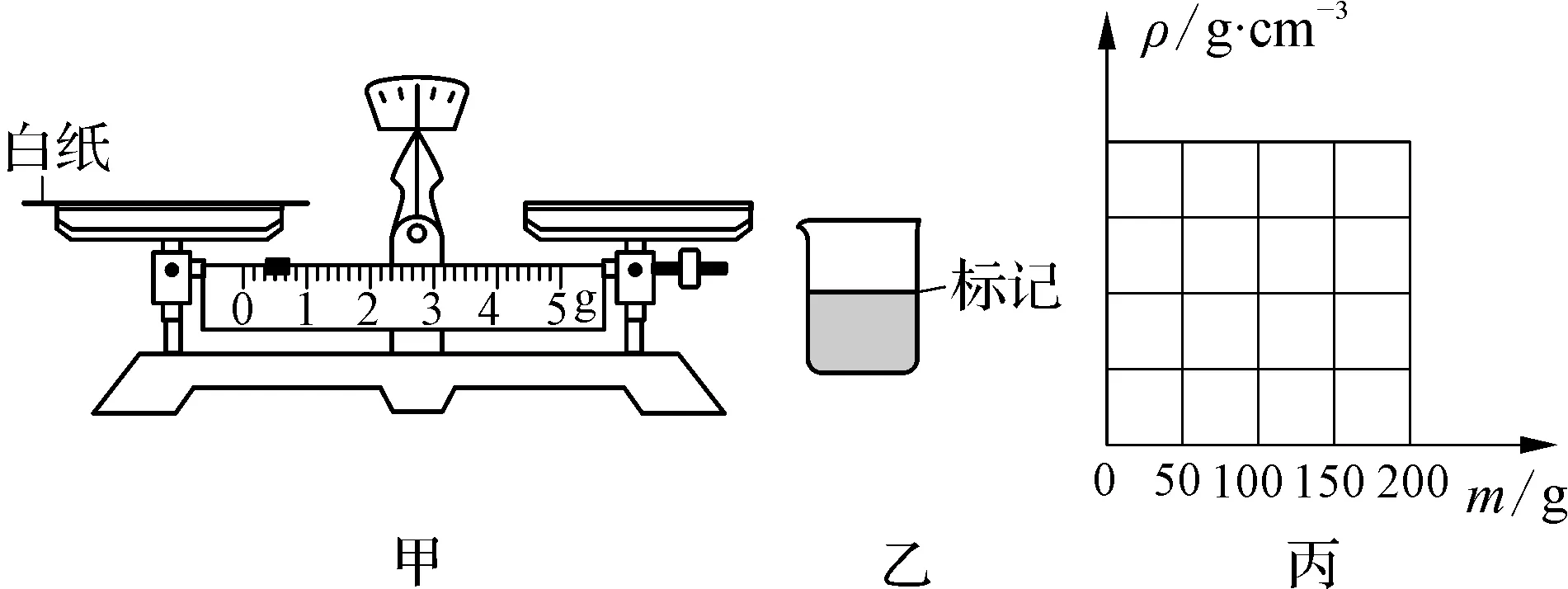
图1
(1) 调节天平时,将天平放在水平台面上,将游码移至标尺左端的“0”刻度线处,若此时指针偏向分度盘中央刻度线的左侧,应将平衡螺母向调节,使指针对准分度盘中央的刻度线。
(2) 为称量出2 g盐,小红先将一张白纸放在天平左盘上,仅移动游码,天平再次平衡时,游码示数如图1甲所示,则白纸的质量为g;接下来,应该先将游码移至g处,再用勺子向左盘的白纸上逐渐加盐,直至天平再次平衡。
(3) 用量筒量取50 mL的水,并全部倒入烧杯中,再将2 g盐全部倒入烧杯中(假设加盐后烧杯中水的体积不变),则小红所配置的盐水密度为g/cm3.
(4) 小红发现可以用实验中的天平和烧杯制作“密度计”。她测出空烧杯的质量为50 g。然后在烧杯中加水,使烧杯和水的总质量为100 g,并在水面位置处做好标记,如图1乙所示。测量液体密度时,将待测液体加至“标记”处,用天平称量出烧杯和液体的总质量m。为方便使用该“密度计”,小红做了如下的使用说明:
① 图1丙中横坐标表示m,纵坐标表示待测液体密度ρ。请在图1丙的坐标系中画出ρ-m图象,并在坐标轴上标出ρ的最大值。
② 理论上,该“密度计”可以鉴别密度差异不小于g/cm3的液体。
本题的第(4)问涉及“密度计”的制作,体现了创新性的要求,对学生的思维能力提出了较高要求。如果在中考复习中没有对学生进行方法的指导,形成结构化的知识体系,学生较难实现新情境中的知识迁移,笔者根据教学实践提出以下中考复习策略。
3 中考复习策略
3.1 展示真实情境,唤醒学生的基础知识
中考复习如果仅仅是知识的罗列,不仅上课枯燥,学生提不起兴趣,知识的提取也比较缓慢,学生的思维依然会停留在识记的初级阶段。真实情境的展示能够激发学生的学习热情,能够在解决真实问题的过程中快速回顾相关知识,为知识的结构化做好充分准备。笔者以问题解决为线索,为学生提供了小石块、酱油等真实物体及相关器材。
问题1:如何测出小石块的密度?请你说出原理、器材和实验步骤。
问题2:如何测出酱油的密度?请你说出原理、器材和实验步骤。
通过问题的回答,学生能够快速唤醒相关基础知识和基本技能,这些基础知识和基本技能的复习是基于真实的情境、通过学生的展示等互动活动来完成的。对于暴露学生的前概念提供了交流平台,为后面的思维提升打下良好基础。
3.2 设计劣构问题,激发学生思维
一般来说,一个良构问题只有一个满意的解决方案,而劣构问题又称非良构问题,是指富有多种解决方案、多种解决途径的问题。[2]劣构问题对学生的思维提出了较高的要求。在学生通过情境重温了基础知识和基本技能后,教师提出问题3:如果没有量筒(或石块较大无法直接放进量筒),如何测出石块的密度?教师提供了天平、烧杯和适量的水,要求学生将设计的方案用画图的方式表达出来,其目的是将学生的思维过程显性化。
由于没有确定的方案,学生会设计出不同的方案,再通过同学自评、小组互评等形式针对不同方案的优劣、密度测量的误差等方面进行讨论、交流。特别是误差的分析,有助于学生对误差产生的原因及减小误差的方法进行深入的思考。烧杯中水的质量在石块拿出前需要准确测定,而石块拿出后水加至标志处的总质量也需要准确测定,两次质量之差除以水的密度即为石块的体积。同时要关注以下问题:如何用量筒补水?石块如果吸水又如何处理?该过程体现了劣构问题对思维的较高要求,并且融入了标记法、等体积法、转换法等科学方法,让学生进一步体会到科学方法在科学发展中的重要作用。
3.3 建立物理模型,解决中考真题
在问题3解决的基础上,教师可以引导学生自主提出问题4:如果没有量筒,给你天平、空瓶子和适量的水,你如何测出酱油的密度?学生能够运用在空瓶中加满水的方法解决这一问题,从而深化对等体积法的认知和理解,并能够在此基础上建构等体积法的物理模型。再通过对中考真题的解决,为这一模型的巩固提供实践和应用的机会,学生很有成就感和获得感。
例2(2019年南京):在科技节活动中,有一项挑战项目:如图2所示,A、B、C、D是装满了某一种材料(细盐、铁粉、米粉中的一种)的四个不透明的轻质密闭容器,要求在不打开容器的前提下,将其中装有相同材料的两个容器挑选出来,提供的器材有:

图2
① 与密闭容器同样的空容器各一个;
② 天平和水。
按下列步骤在空白处填上适当的内容。
用天平分别测出图中四个密闭容器的质量mA、mB、mC、mD;
(1);
(2) 若满足关系式:(用测量的物理量表示),则A、C两容器中所装材料相同。
学生利用等体积法将瓶子的容积算出来,再求出不同物质的密度,并进行对比即可,简洁明了,体现了物理建模的实用性和重要性。
3.4 培养创造能力,促进深度学习
在建构模型的基础上,学生能否实现创新和创造?这是教师需要思考的问题,也是培养学生高阶思维的应然要求。2019年南京市中考题的密度实验和2020无锡市中考题的的第(4)小问都有异曲同工之妙,都利用了前面所讨论的等体积模型。那又如何在此基础上进一步提升学生的思维,达到深度学习的目的呢?笔者做了如下尝试。
如图3所示,利用一架没有砝码的天平,师生共同设计了一个“密度计”。取相同体积的某种液体(如盐水)和水,通过调节游码让天平平衡。则通过计算可在游码所对应的位置标上对应的密度值。这依然是等体积物理模型的拓展应用,通过教师的追问可以对学生提出更高的思维要求,如:若左盘液体的密度比水小,该密度计是否还能使用?想要使用如何去改进?该密度计的刻度是均匀的,而用吸管做的密度计刻度线为什么不均匀?该密度计的分度值(即无锡市中考题中所提出的可以鉴别密度差异不小于多少g/cm3的液体)和量程是多少?该密度计的分度值和量程与所装液体的体积有什么关系?通过教师的追问,能够将学生的思维引向深处,从而达到深度学习的目的。

图3

图4
同样还可以引导学生运用等质量的方法,如图4所示,在天平的两个托盘上分别放置相同的有刻度的小杯子,在左边的小杯子加入20 ml某种液体,利用注射器在右盘的小杯子加入适量的水直至天平平衡,通过计算可以在对应的刻度上标上相应的密度值,这样天平和右边的小杯子又可以组成新的“密度计”。同样可以通过学生的评价和教师的追问对该密度计进行深入的探讨,如:比较甲、乙两种密度计的异同,对比两种密度计,谁更具优势?这样通过师生共同设计、制作密度计,培养了学生的创新能力,通过评价和问题串促进了学生的深度学习和高价思维的发展。
4 教学启示
4.1 培养学生的问题意识
对于问题4笔者并没有直接提出,而是问学生:如果你是教师,你会提出什么样的问题?学生在经过思考后提出了问题4,有同学还提出了问题5:如果没有天平,我们又如何测出物体的密度?提出问题比解决问题更重要,为了让学生提出有意义的问题,需要教师精心设计和引导,给学生提供支架,这样学生才能逐步养成问题意识和批判质疑精神。
4.2 培养学生建模的意识
中考复习需要我们和学生一起将零散的知识结构化,而培养学生的建模能力有助于学生将知识结构化。在解决2019南京市和2020无锡市中考题的过程中,我们利用等体积模型解决了这一问题。这样做可以给学生很好的启示,通过建构物理模型能够促进知识的结构化,从而将多题归一的思想落到实处。[3]
4.3 培养学生的创新意识
在密度计的设计过程中,利用等体积法可以制成密度计。如果学生能够在教师的引导下利用等质量法再设计、制作密度计,就能够激发学生举一反三和创新意识,而这种意识需要我们用心去培养、精心设计和准备,不断为学生搭建思维的阶梯,这样才能实现活水有源,攀登有梯。
上述三种意识又具有较强的逻辑关系,有了问题意识,才会想到去寻找合适的路径或模型去解决问题;真正解决了问题,才会有创新和创造的本领;而有了创新和创造,才会进一步提出新的问题,这样形成了物理学习的闭环,在不断螺旋上升的过程中,学生的核心素养也就能够得到稳步的提升。
5 结语
深度学习的根本目的是促进学生科学思维的发展,[4]而问题是思维的引擎,问题解决不仅是深度学习的重要目标,同时也是实现深度学习的重要途径。[5]所以,通过问题解决能够促进学生的深度学习,从而提升学生的科学思维能力。因此,在中考复习过程中,需要教师创设真实情境、设计有效问题,促使学生围绕一系列问题展开深度思考,让学生的学习不再被动,而是触及灵魂的深度学习,即在知识结构化的同时,充分发展学生的模型建构、科学推理、科学论证、质疑创新等科学思维能力,提升学生的核心素养。

