基于DMC预测控制算法的冷凝器压力控制

黄裕雯，卢川，夏虹，吕新知，彭彬森

1. 哈尔滨工程大学 核安全与先进核能技术工信部重点实验室，黑龙江 哈尔滨 150001

2. 中国核动力研究设计院 核反应堆系统设计技术重点实验室，四川 成都 610000

冷凝器作为核电厂二回路中的一个重要的换热设备和辅助设备，在热力循环过程中起到冷源作用，汽轮机排出的乏汽经冷凝器后温度和压力都有所降低[1]。冷凝器的压力及真空度都是汽轮机运行的重要参数，都会影响机组的安全运行，对核电厂冷凝器的压力进行有效的控制是非常必要的[2]。比例-积分-微分(PID)控制由于其原理比较简单，而且容易实现，经常被用于工业控制系统上[3]。但对于核电厂冷凝器这种具有迟延性以及参数时变特点的对象而言，传统的PID控制方法在控制效果上不理想，调节时间较长，超调量较大[4]。PID控制中以线性的方式近似代替非线性，其调节精度不高，不够精准。预测控制是近年来被提出的适应于过程控制的一种先进的控制算法，可适用于核电厂运行这类复杂非线性化的过程，它具有更好的处理非线性系统的能力，特别是动态矩阵预测控制算法在复杂迟延对象上也具有比较明显的优势[5]。目前，预测控制在核电厂冷凝器压力控制上的应用研究比较少，本文将建立核电厂冷凝器的动态数学模型，研究冷凝器压力控制的方法，在传统PID控制方法的基础上，设计动态矩阵预测控制器，并与PID控制器的控制效果进行对比，为核电厂冷凝器压力的控制提供新的控制方案。

1 核电厂冷凝器建模研究

1.1 冷凝器动态数学模型

在建模过程中，假定冷凝器的压力和内部汽水的温度是时间的函数；在对换热量的计算中，把冷却管束按照一簇进行处理，用总体传热系数求出蒸汽凝结的放热量，把其中的蒸汽视为理想气体，并且不考虑不可凝结气体的影响。图1为单流程冷凝器的结构简图。

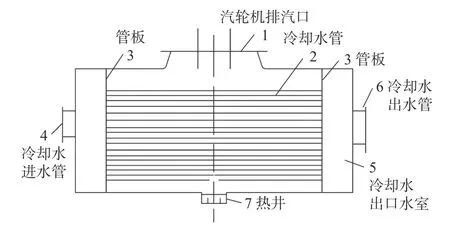
图1 单流程冷凝器结构

冷凝器动态数学模型由3个响应数学模型组成，包括冷却水量扰动响应数学模型、蒸汽负荷扰动的响应数学模型和压力扰动的响应数学模型。核电厂冷凝器内涉及到的传热过程是分环节进行的，所以本文建立分环节的动态数学模型。

冷却水量扰动响应数学模型为

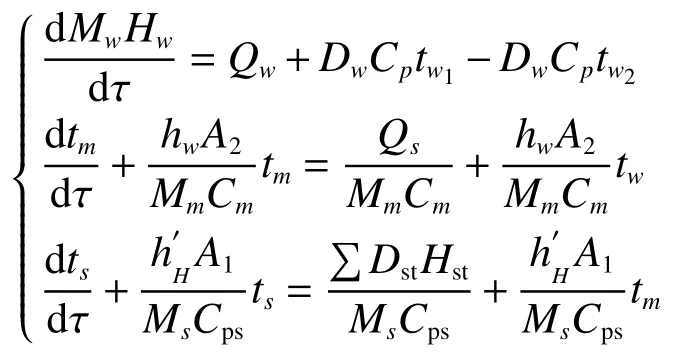
式中：Mw为冷凝器冷却管道的储水质量，kg；Mm为冷凝器冷却水管的质量，kg；Ms为冷凝器汽侧饱和蒸汽的储气量，kg；Qw为冷却水和冷却管的换热量，W；Qs为蒸汽与冷却水管外壁之间的凝结换热量，W；tw为冷却水的平均温度，°C；tw1、tw2为冷却水的进口、出口温度，°C；ts为饱和蒸汽的平均温度，°C；tm为冷却水管道平均壁温，°C；A1、A2为饱和蒸汽、冷却水与冷却水管壁之间的换热面积，m2；∑DstHst为所有进入和排出冷凝器的蒸汽的总能量，W；Hm为冷却水的平均比焓，J·kg-1且Hw=Cdtw；Cp、C∞x、Cm为冷却水、冷却水管、蒸汽的比热容J·(kg·◦C)-1；D为冷却水流量kg·s-1。

蒸汽负荷扰动的响应数学模型为

式中：Rs为饱和蒸汽的气体常数，J·(kg·K)-1；Fst为单位时间进入冷凝器壳侧空间得所有蒸汽量，kg·s-1；Fost为冷凝器其他进气量，kg·s-1；Fc为蒸汽的主凝结量，kg·s-1，且；Fss为抽气器抽出的蒸汽量，kg·s-1；Ff为进入冷凝器内疏水的闪蒸量，kg·s-1。

压力扰动的响应数学模型为

式中：Qw为冷却水和冷却管内壁之间的对流换热量，W，且Qw=hwA2(tm-tw)；Qs为蒸汽与冷却水管外壁之间的凝结换热量，W，且；hw为冷却水与冷却水管之间的对流换热系数，hw=，Re为雷诺数，Pr为普朗特数；为饱和蒸汽与冷却水管道之间的凝结换热系数。

本文整理相关文献上有关大亚湾核电站900 MW核电机组冷凝器的实际参数[6]如表1，并以此作为依据进行计算。

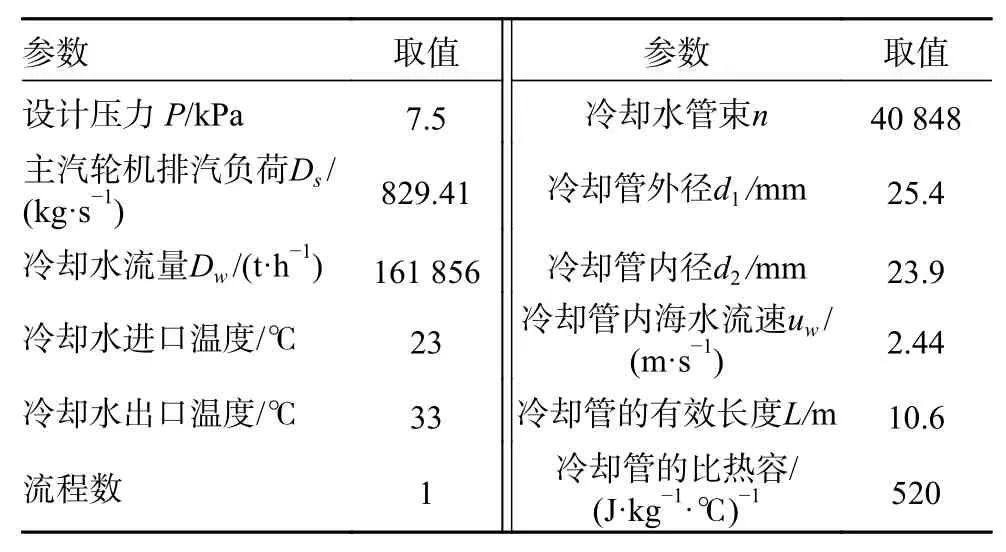
表1 冷凝器参数表

1.2 动态数学模型验证

从图2仿真曲线看出，冷却水量从设计工况44 960 kg·s-1分别跃增10%、20%和30%时，冷凝器压力从设计工况的7.5 kPa开始下降，分别经过32.69 s、41.06 s和48.93 s达到新平衡状态；冷却水流量从设计工况44 960 kg·s-1跃减10%、20%和30%时，冷凝器的压力从设计工况的7.5 kPa开始上升，分别经过约36.38 s、41.79 s和74.39 s达到新平衡。

冷却水流量从2个方面影响冷凝器压力：在凝结换热量基本保持不变时，冷却水量变化会使冷却水平均温度随之改变，从而影响传热端差；在冷却管管径不变的前提下，冷却水量改变，即冷却水流速改变，从而影响传热系数。这2个因素的改变进而使冷凝器压力发生变化。

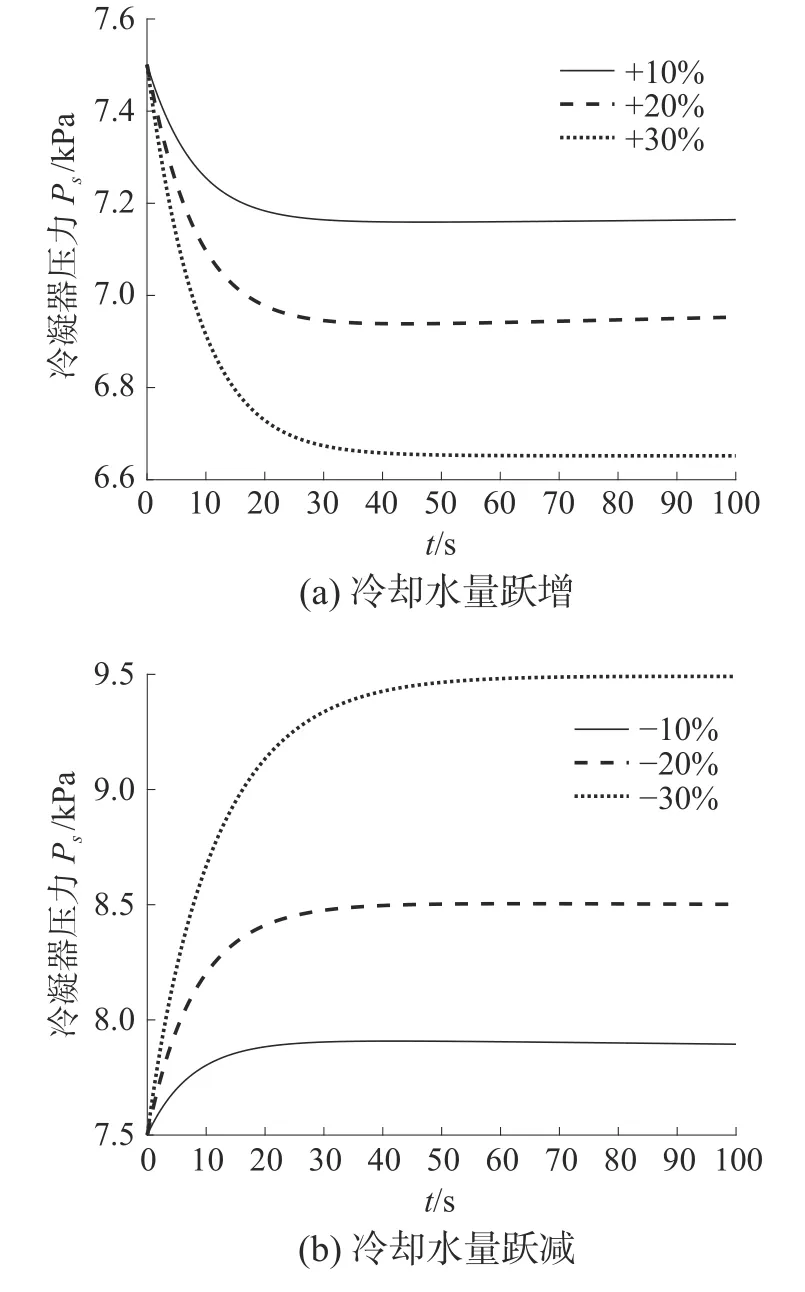
图2 冷却水流量变化时冷凝器压力的变化趋势

从图3仿真曲线看出，蒸汽负荷从设计工况872.192 kg/s跃增10%、20%和30%时，冷凝器的压力会从设计工况的7.5 kPa开始下降，分别经过19.54 s、28.34 s和36.46 s达到新的平衡状态；蒸汽负荷从设计工况872.192 kg/s跃减10%、20%和30%时，冷凝器的压力会从设计工况的7.5 kPa开始上升，分别经过31.05 s、40.52 s和43.72 s达到新平衡。

蒸汽负荷发生阶跃变化时，压力的改变是一个平缓的过程。因为蒸汽负荷跃增会导致传热端差变大，从而提高冷凝器的蒸汽换热效率，冷却水所带走的汽化潜热增加也加速冷凝器内主蒸汽的凝结，从而延缓了压力的上升过程。

从图4仿真曲线看出，当冷凝器压力阶跃增加10%、20%和30%时，冷却水的出口温度从设计工况的33.3℃逐渐升高，经过40.07 s、55.82 s和70.45 s达到新平衡；当冷凝器压力阶跃减少10%、20%和30%时，冷却水的出口温度从设计工况的33.3℃开始降低，经过37.61 s、50.65 s和69.47 s达到平衡。

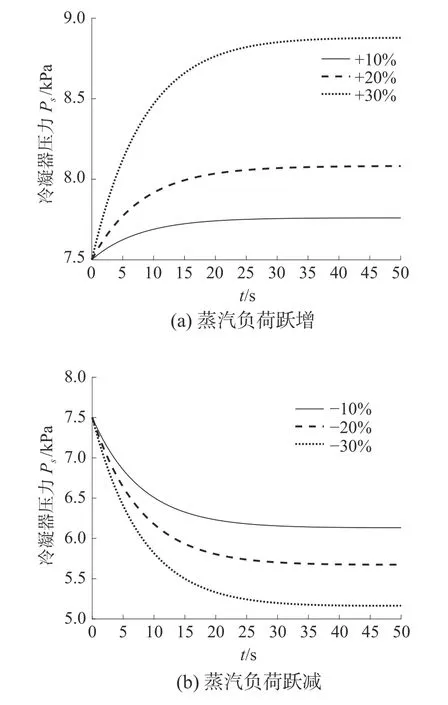
图3 蒸汽负荷变化时冷凝器压力的变化趋势

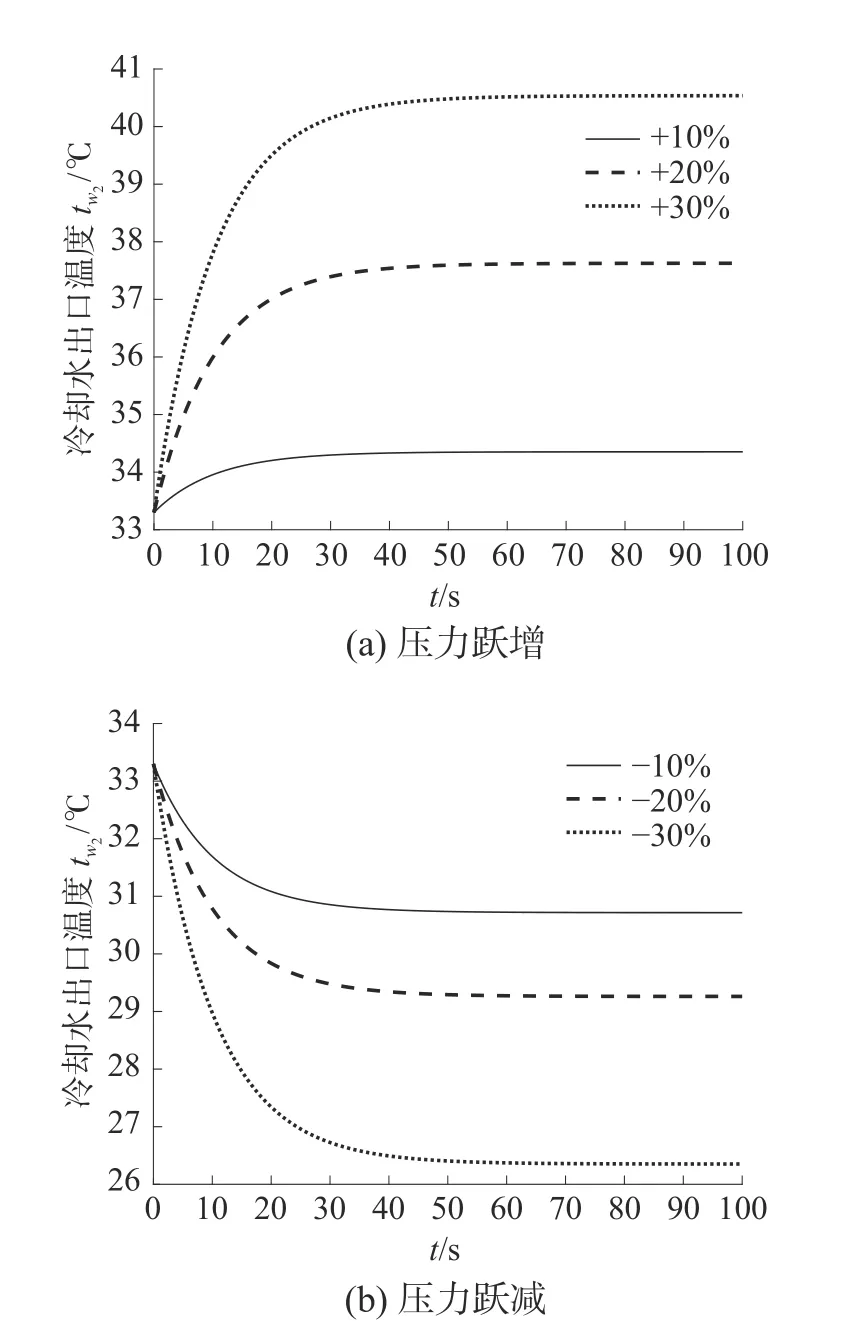
图4 压力变化时冷却水出口温度的变化趋势

1.3 传递函数模型

冷却水量扰动响应数学模型传递函数关系包括冷却水平均温度对冷却水量响应的传递函数关系G1(s)、冷却水管壁温对冷却水平均温度响应的传递函数关系G2(s)和蒸汽平均温度对冷却水管壁温响应的传递函数关系G3(s)。

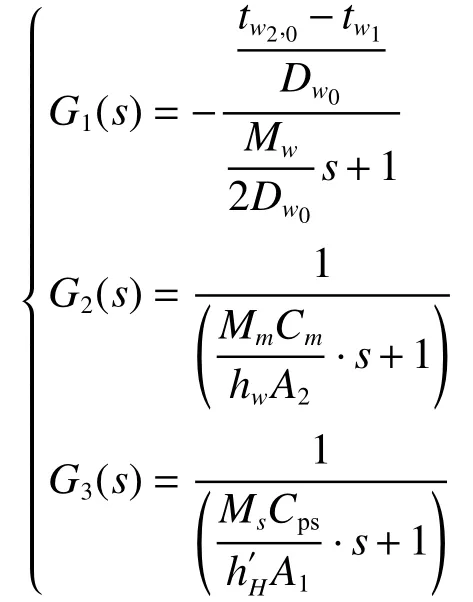
蒸汽负荷扰动的响应数学模型传递函数关系为

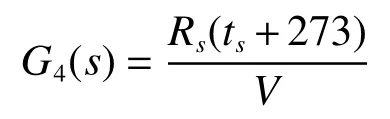
压力扰动的响应数学模型传递函数关系，包括冷却水管壁温对蒸汽平均温度的传递函数关系G5(s)和冷却水出口温度相关传递函数关系G6(s)。

2 动态矩阵预测控制算法的研究

动态矩阵预测控制（dynamic matrix predictive control, DMC）算法是一种基于对象阶跃响应的预测控制算法，它适用于渐近稳定的线性对象[7]。DMC算法的计算过程主要包括离线准备和在线计算两部分[7]。在线计算的环节包括初始化和实时控制，初始化主要是进行参数的确定[7]。在初始化阶段需要确定系统的采样周期、预测时域和控制时域等参数[7]。在实时控制阶段，检测当前实际输出值y，作为预测初始值，由计算误差进行校正得到校正后的预测输出值，从而得到新的预测初始值，同时计算对应的控制量，并得到该控制量作用下的预测输出用于下一步的实时控制[7]。整个DMC算法是由预测模型、滚动优化和反馈校正这3部分组成[7]。动态矩阵预测控制算法的原理结构如图5所示。

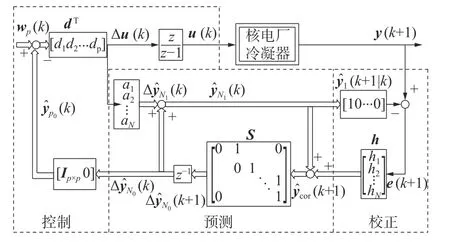
图5 动态矩阵预测控制算法的原理结构

2.1 非参数模型的建立

在传递函数的阶跃响应曲线中以0.1 s的采样周期进行离散点采样，采样直至响应曲线趋于平稳。同时取建模时域为1 000，共有1 000个采样点，核电厂冷凝器压力的动态信息由有限集合H=[a1,a2,···,aN]T进行描述。表2为非参数模型的值。

表2 非参数模型值

本文取预测时域P=1000，控制时域取M=1。可根据式(1)进行核电厂冷凝器压力预测值的计算：在k时刻，假定控制作用不变，对未来时刻的初始预测值yˆ0(k+i|k),i=1,2,···,N，则当k时刻有M个连续的控制增量，那么在这些控制增量作用下未来时刻冷凝器压力的输出值[7]为

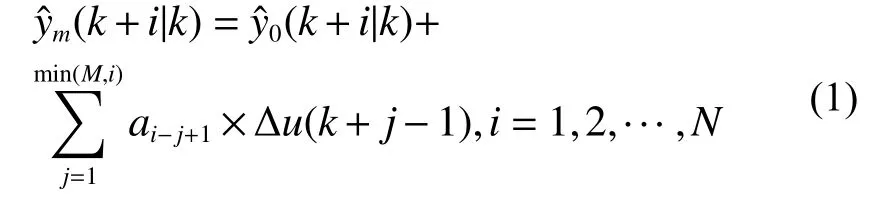
只有一个增量Δu(k)时，即M=1，可算出在其作用下未来时刻的输出值[7]：

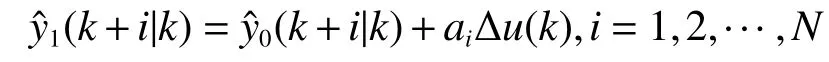
2.2 滚动优化

在每一个时刻k，要确定从该时刻起的M个控制增量即冷却水流量的变化量，使得在其作用下未来P个时刻的冷凝器压力的预测值尽可能接近给定的冷凝器压力的期望值w(k+i)。对于这个问题可以建立如式(2)的优化性能指标[7]：

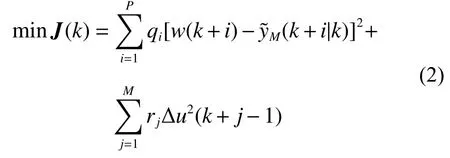
式中：q为控制跟踪误差的权系数，rj是制约控制量变化的权系数。

式中：

2.3 反馈校正

在下一采样时刻冷凝器压力的实际输出y(k+1)与预测模型算出的预测输出值进行比较，构成输出误差。

利用校正向量以加权的方式对输出误差进行校正。校正后的冷凝器压力预测向量为

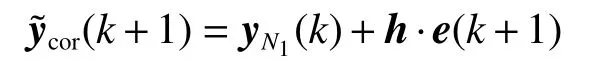
式中：

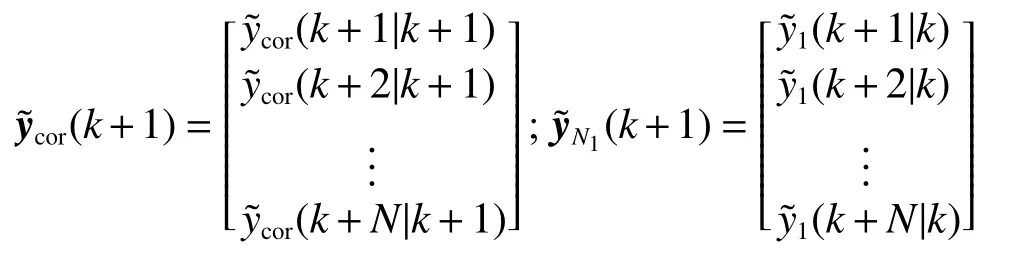
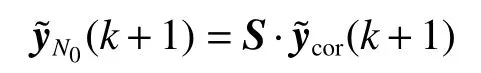
2.4 DMC预测控制系统设计

本文将DMC预测控制器与核电厂冷凝器传递函数模型在仿真平台上连接[8]，如图6所示。

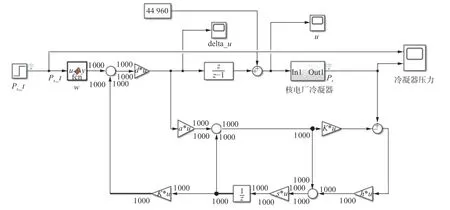
图6 核电厂冷凝器DMC预测控制系统

设预测算法采样周期为0.1 s，建模时域N=1000；预测时域P=1000；控制时域M=1；误差权系数Q=[500,500,···,500]1×π，控制权系数R=[0.1,0.1,···,0.1]1×M，校正向量h=[0.0025,0.0025,···,0.0025]h×π。

3 仿真结果分析

根据DMC预测控制算法的设计原理，设置DMC预测控制器参数，可以得到蒸汽负荷跃增10%、15%和20%时，DMC控制算法的核电厂冷凝器压力的仿真曲线，同时与PID控制器下最佳控制效果的仿真曲线作对比[9-11]，如图7～图9所示。

从图7(a)中可知，蒸汽负荷跃增10%时，冷凝器压力控制过程中，PID控制器的调节时间约为44.5 s，动态最大值在9.7 kPa左右，超调量为29.69%，稳态误差值为0.009 6；动态矩阵预测控制器的调节时间约为30.79 s，动态最大值约9.5 kPa，超调量为26.78%，稳态误差值为0.002 1。由图7(b)可知蒸汽饱和温度从40.409 6℃开始降低，在DMC控制器和PID控制器下分别经过约47.08 s、66.21 s后趋于稳定值。

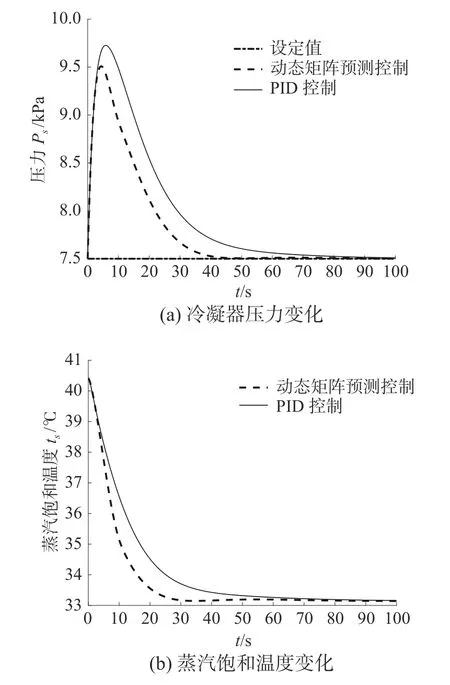
图7 PID与DMC预测控制仿真结果对比（蒸汽负荷跃增10%）

由图8(a)可知，蒸汽负荷跃增15%时，PID控制器的调节时间为55.14 s，动态最大值约10.1 kPa，超调量为34.51%，稳态误差值为0.023 5；动态矩阵预测控制器的调节时间约为33.8 s，动态最大值约10 kPa，超调量为32.63%，稳态误差值为0.004 9。由图8(b)可知蒸汽饱和温度从40.409 6 ℃开始降低，在DMC控制器和PID控制器下分别经过约53.15 s、89.29 s后趋于稳定值。

由图9(a)可知，蒸汽负荷跃增20%时，PID控制器的调节时间为79.36 s，动态最大值在11.2 kPa左右，超调量为49.12%，稳态误差值为0.075 6；动态矩阵预测控制器的调节时间约为51.45 s，动态最大值约11 kPa，超调量为46.74%，稳态误差值为0.018 8。由图9(b)可知蒸汽饱和温度从40.409 6℃开始降低，在DMC控制器和PID控制器下分别经过约78.41 s、92.68 s后趋于稳定值。

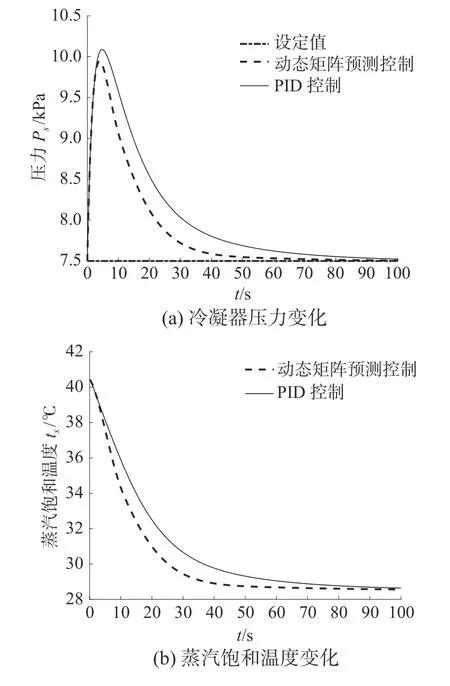
图8 PID与DMC预测控制仿真结果对比(蒸汽负荷跃增15%)

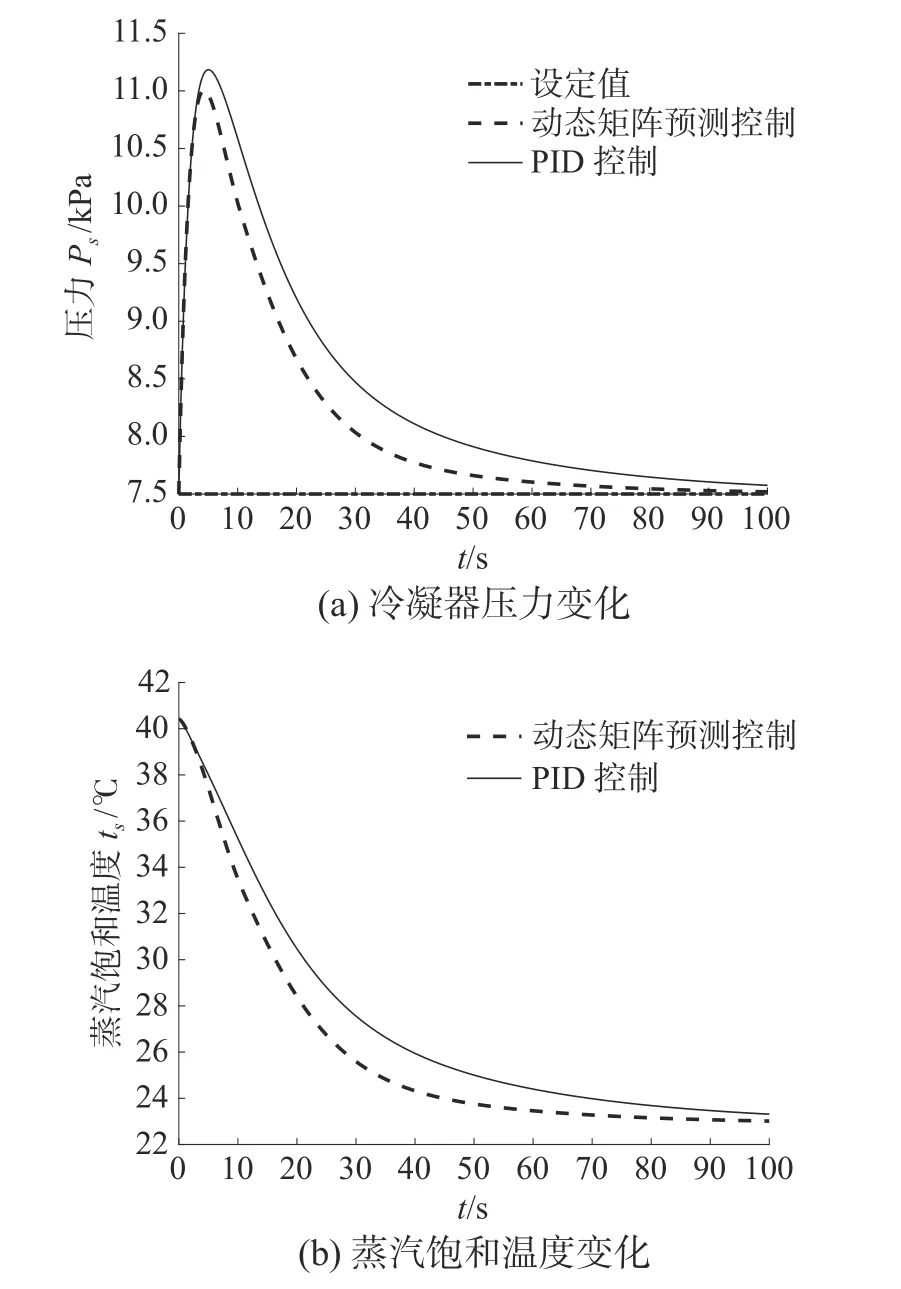
图9 PID与DMC预测控制仿真结果对比(蒸汽负荷跃增20%)

从图7～9对比图可以明显看出动态矩阵预测控制效果优于PID控制效果。相对于PID控制，动态矩阵预测控制具有调节时间更短、抗干扰能力更强、超调量更小的特点[12]，系统能较为快速稳定地到达设定值。因此，对于核电厂冷凝器真空度的控制，动态矩阵预测控制能使冷凝器压力较为稳定快速地变化到设计工况的设定值，且该控制器对环境压力的影响也有一定的抗扰能力，使得核电厂冷凝器中压力调节的问题得到改善。

4 结论

本文通过集总参数法建立核电厂冷凝器模型，并在分析其动态响应时间滞后的原因后，通过仿真平台搭建预测控制系统。

1) 运用模型预测、滚动优化等原理，将冷凝器的压力作为目标，设计了动态矩阵预测控制器，并且通过仿真实验验证该控制器对核电厂冷凝器压力控制系统的控制效果比较理想。

2) 在核电厂压力控制的调节过程中，动态矩阵控制系统能够缩短调节时间、减小超调量，使得系统的实时控制能力和抗干扰能力有一定的提高，弥补了传统 PID 控制上的不足。