基于时间构建技术的机载高精度同步系统设计

周荣坤，樊锐，苏武海，马磊，张鑫龙

1. 中国电子科技集团公司 电子科学研究院，北京 100041

2. 中国科学院 微电子研究所，北京 100029

双/多基地雷达通过将发射和接收天线部署在不同地理位置或平台上，可有效应对隐身目标、强电子战能力目标、低空突防目标以及反辐射导弹等新型威胁，因此已经成为探测领域研究的热点[1]。尤其是利用了隐身目标侧向散射、前向散射增强区和多普勒拍频等特性，可大幅提升对隐身目标的定位精度[2-6]。机载双/多基地雷达由于受无线信道同步秒脉冲误差制约，难以达到很高精度的同步要求。在电力、广电、车载系统等应用领域，研究人员提出了多种时间同步方式[7-11]，但应用环境和技术路线难以满足机载应用要求；王延年等[12]结合北斗/GPS 多模同步的本地时间基准，利用 ARM9 Kernel 和 FPGA 实现了主、从站同步误差控制在 200 ns 以内 ；李倩等[13]提出了一种基于 FPGA 的时间同步方法，虽然可以应用于机载环境，但难以满足机载双/多基地雷达高精度同步要求。本文提出了一种基于时间构建技术的机载高精度同步系统，分析了频率和秒脉冲沿差测量和校准的原理，分析了同步精度误差、校频误差，以及时间同步维持的效果，可满足部分机载条件下的双/多基地雷达同步要求。

1 系统组成

基于全球导航卫星系统（global navigation satellite system，GNSS）多模的高精度时间同步系统由GNSS多模接收机模块、沿差和频差测量模块、微处理器模块、原子钟模块、时间和频率校正模块组成，见图1。

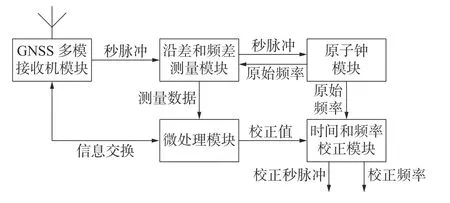
图1 基于GNSS多模的时间频率同步系统

GNSS多模接收机模块用来接收GNSS卫星或地面增强系统的多模信号，并产生可用于同步系统定时及校频的秒脉冲信号。该模块受微处理器模块的控制，并主动报告自身当前状态。

原子钟模块用来产生原始频率信号。校正该模块能够增加输出频率的准确度；校正分频产生的秒脉冲信号，也可作为系统的输出信号。

沿差和频差测量模块对GNSS多模接收机与原子钟模块输出秒脉冲间沿差进行测量，同时测量GNSS多模铷钟的原始频率。

微处理器模块接收处理沿差和频差测量模块发送的测量数据，并监测和控制整个系统。

时间和频率校正模块通过接收来自微处理器的校正数据，校正秒脉冲沿差及频率，完成对时间/频率的校正。同步需要完成时间确定与频率校准。作为实现高精度时间同步的核心，高精度测量和校正需要尽量准确地完成对时间偏差及频率偏差的测量。

2 频率测量和校准

由频率准确度的定义，可以得到：

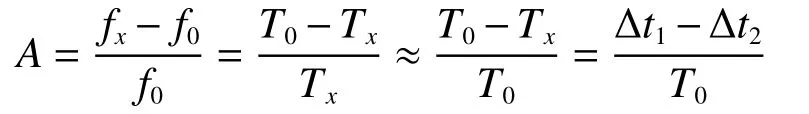
式中：fx为量测得到的频率，f0为标称频率，Tx为被测频率周期，T0为标称频率周期，Δt1、Δt2为用比时法测准确度的前后沿时间间隔。比时法通过测量时间间隔T前后2次GNSS多模秒脉冲及原子频标秒脉冲上升沿的沿差，计算原子频标的秒脉冲频率准确度，原理如图2。

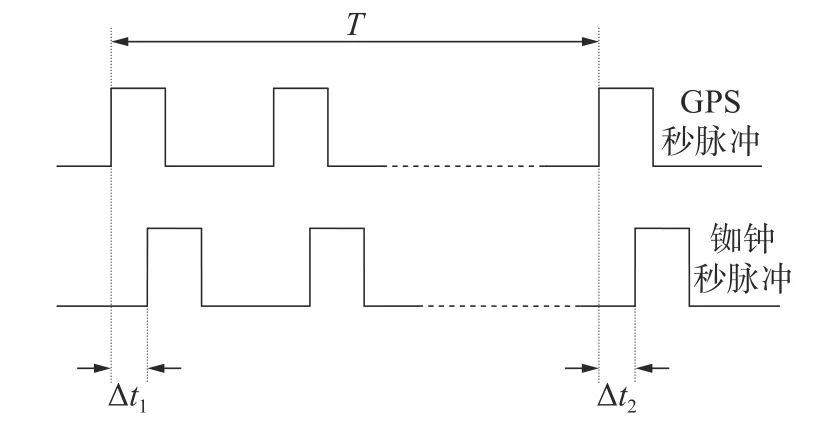
图2 比时法测量频率准确度原理

考虑到测频周期较短时，秒脉冲频率标准的短期稳定度较差，秒脉冲频率值的随机起伏会给准确度的测量带来较大影响，因此，在选取比时法的时间测量间隔T时，对秒脉冲频率准确度的测量应选取较长的时间片段；在选取对应时间频率稳定度时，应遵循“以高测低”的原则，比被测秒脉冲频率准确度高一个数量级。在这种情况下，选用比时法测量时间间隔Δt1和Δt2，应谨慎选择测频时间T，以确保所引入的量化误差A比被测秒脉冲频率标准准确度小一个数量级[14]。

例如某铷原子频标标称秒脉冲频率为10.23 MHz，频率准确度为2×10-10，秒稳定度为1.42×10-11，测量沿量化误差为1 ns。则期望秒脉冲频率校到准确度为1×10-11时，测量时间间隔T为

根据准确度公式，秒脉冲频率校正值最大为

直接数字频率合成（direct digital dynthesis，DDS）的频率可在几个纳秒内瞬时改变，且具备相位连续、能够数字化编程、方便调制的优势，可根据需要产生指定频率和初始相位的正弦波。某48位相位累计器，最高工作频率为300 MHz，其频率分辨率为

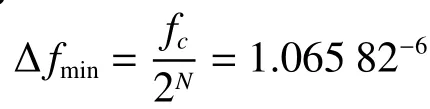
每当来一个时钟信号，DDS相位寄存器就增加一个M步长，然后将其输出和相位控制字进行加和，并在正弦查找表中查表得到数字量化信息。相位寄存器每经过2N/M次fc时钟，回到最初始的状态，整个DDS生成一个正弦波。此正弦波的周期时长和频率分别为

DDS的结构如图3所示。

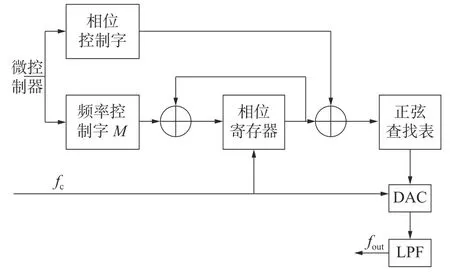
图3 DDS基本结构示意

3 秒脉冲沿差测量和校准

在完成频率校正以后，多次测量GNSS多模秒脉冲和原子频标秒脉冲之间的间隔Δti，求出平均间隔Δt：

本文选用14位相位控制字的DDS。DDS的相位分辨率为

按10 MHz频率算，1 ns约对应3.6°。将沿差转换为相位值，输入相位控制字，使10 MHz信号的相位对齐，即完成GNSS多模秒脉冲的对齐。

4 误差分析

文中同步系统的同步指标：秒脉冲上升沿同步精度为最大20 ns；频率校准精度为2×10-12。

4.1 秒脉冲沿同步精度误差分析

以GNSS多模时间同步系统的各个分站为基础，利用GNSS多模接收机输出的秒脉冲和时间误差补偿值可求得GNSS多模系统时间；铷钟分频产生的秒脉冲以GNSS多模系统时间为基准校准。目前GNSS多模终端厂商虽然一直在推动技术进度，但是用秒脉冲及时间误差补偿值进行计算得到的GNSS多模系统时间和真实系统时间之间存在误差，该误差造成了站间的同步误差。使用某GNSS多模接收机，该误差是2 ns和6 ns。

测量沿差使用的高精度测量模块，其分辨率达到0.1 ns，精度达到1 ns。

采用DDS技术来进行校频，因为被校频率到目标频率之间的偏差为10-4数量级，远远大于校频的精度（10-6数量级），DDS所产生的误差几乎可忽略不计。DDS经过频率合成后，由于噪声影响，所以需要经过低通滤波器或者带通滤波器的滤波，滤波会对输出的波形群产生延时，但是因为该延时是整体的，故频率周期所受到的影响只是很小的一部分，由于该原因造成的铷钟频率同步精度损失可以忽略。

校沿采用DDS技术。由式(1)可知，按10 MHz频率计算，1 ns约对应3.6°，因此相位分辨率远小于校沿同步精度，造成的误差可以忽略不计。

按以上分析，各分站秒脉冲误差主要由GNSS多模秒脉冲误差、测量误差和计算误差引起。设GNSS多模秒脉冲误差为6 ns，测量误差为1 ns，计算误差为1 ns，则2站之间秒脉冲误差在极限情况下为

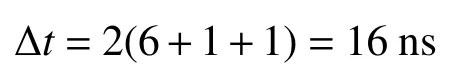
该误差比20 ns更加优越。

4.2 校频误差分析

频率校正误差是由多种因素所造成，主要包括：1) 测量量化误差；2) 计算转化误差；3) 影射转化误差。测量量化误差为1 ns、计算转化误差为1 ns、影射误差为3 ns，单站Δt1-Δt2的最大误差为6 ns；在极端情况下，两站的频率校正方向相反，两站的Δt1-Δt2为12 ns，测频时间为2 000 s。所以，单站的频率偏差为10-12，双站频率偏差准确度最大偏差为2×10-12。

5 时间同步维持分析

铷原子钟存在固有频率偏移问题，同时老化将带来频率漂移问题，导致输出时间与标准时间之间存在一定程度的偏差，t时刻，其与标准时间的时刻差可表示为

式中：k为频率漂移率,Aα为初始频率准确度,E表示初始时刻差,ξ(t)表示频率随机变化所带来的误差。原子钟因频率偏移/漂移与标准时间会产生误差，偏移速度随运行时间逐渐增大。

5.1 理论分析

设分别有2个原子钟1、2，原子钟1的时刻差方程为

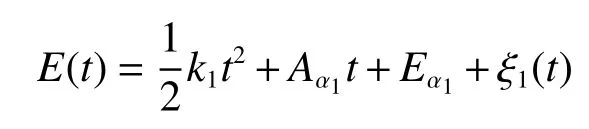
原子钟2的时刻差方程为

忽略频率随机变化带来的误差。运行过一段时间后，在t时刻2个原子钟的差值为

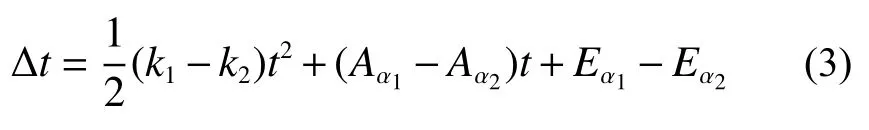
设系统要求2个原子钟的时刻差的最大误差为|em|，解上述方程的根为

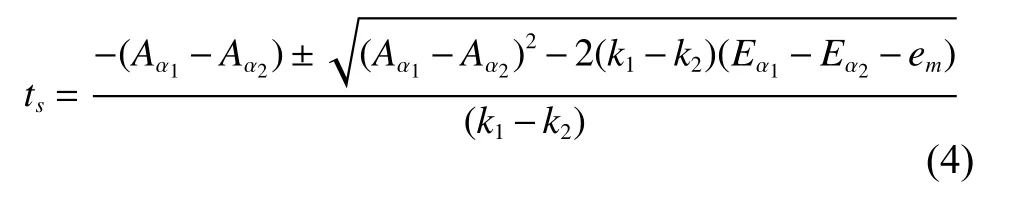
如果2个原子钟的精确度及漂移率参数完全相同，将一直维持同步状态。实际上，每个钟的性能参数不可能完全相同，经过长时间的运行后，时刻差逐渐增加，在某个时刻t不能满足系统对时间同步的要求。

设2个原子钟漂移率差为ε=k1-k2，2个准确度差为δ=Aa1-Aa2，2个起始秒脉冲时刻差为E=Ea1-Ea2。

则式(3)可转化为

则式(4)可转化为

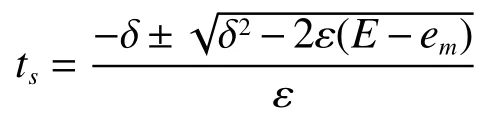
时刻差曲线为抛物线。抛物线的凹凸特性由漂移率差的正、负确定。

5.2 计算结果

分别考虑不同情况下频率准确度差、频率漂移率差的极限情况：

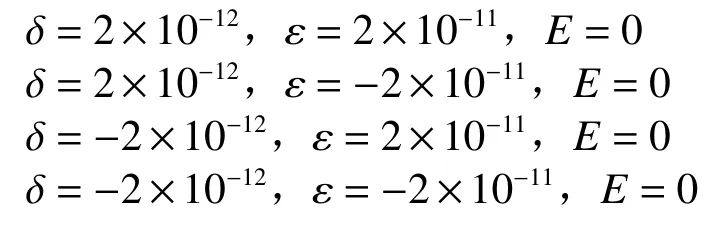
经过1 h的运行，在频率准确度差和频率漂移率差的极限情况下，同步误差和运行时间的关系如图4～图7所示。

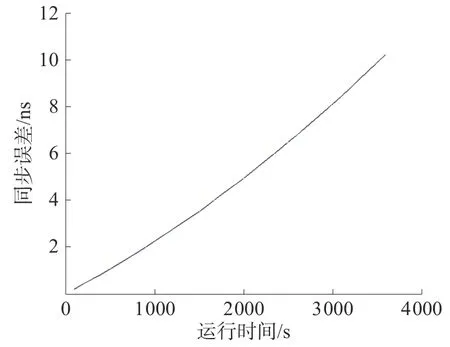
图4 同步误差与运行时间关系（ε ＞ 0, δ ＞ 0）

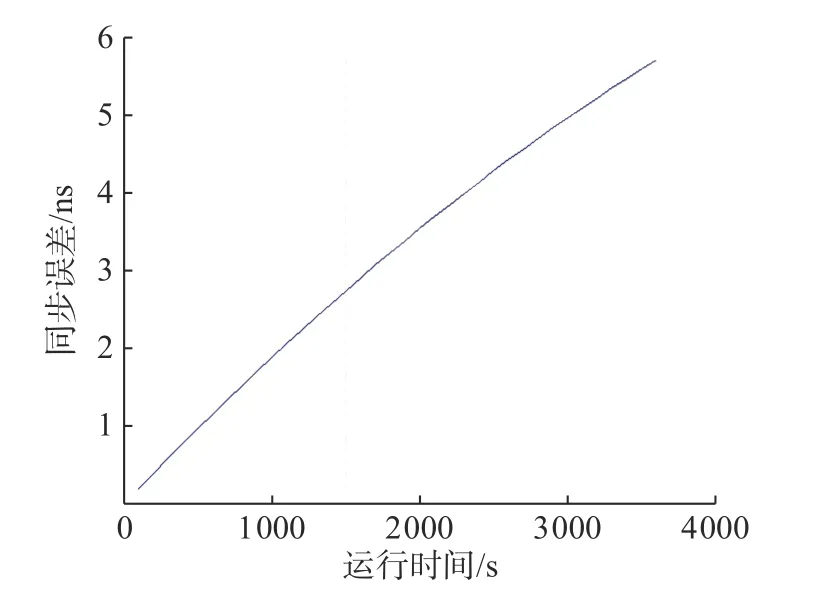
图5 同步误差与运行时间关系（ε ＜ 0, δ ＞ 0）

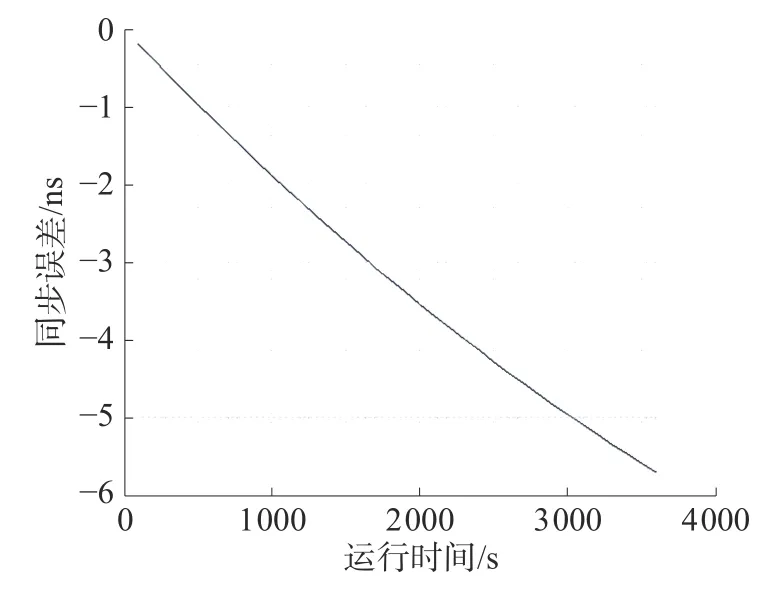
图6 同步误差与运行时间关系（ε ＞ 0, δ ＜ 0）

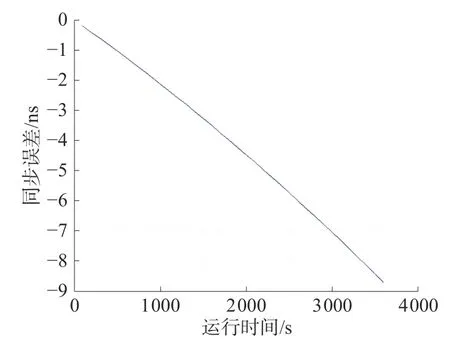
图7 同步误差与运行时间关系（ε ＜ 0, δ ＜ 0）

由此可知道，在频率相位校准后，依靠铷原子钟本身的稳定性可以在一段时间内维持时间同步精度。由于频率准确度误差和老化问题，会引起时刻偏差，因此需要采取措施，每隔一段时间对原子钟进行适当的调整，同时补偿频率，使初始的频率偏移以及漂移接近零，从而使得时刻差符合精度要求。

6 结论

本文提出了基于时间构建技术的机载高精度同步系统设计方法，通过对本同步系统的同步精度误差、校频误差以及时间同步维持的效果进行分析，满足部分机载条件下的双/多基地雷达同步要求，为空基协同探测提供了技术基础。但同时也存在因为维持时间需要周期性对频率进行补偿的问题，这也是后续进一步工作的重点内容。