基于短时傅里叶变换的单相自适应重合闸技术

季鹏，杨竞及，陈芳芳，徐天奇，李晋威

云南民族大学 电气信息工程学院，云南 昆明 650504

单相接地故障多数发生在输电线路上，若属于瞬时性故障，则可以快速重合闸，但在永久性故障下重合闸，会严重威胁系统的安全稳定运行[1-2]。因此，研究具有识别故障性质及熄弧时刻自适应重合闸具有重要意义[3-4]。20世纪80年代葛耀中等[5]提出了“自适应重合闸”的研究方法，即先在故障点处判断出故障的性质，再考虑是否进行合闸操作。

经过多年的研究，业界已经提出了许多判别故障性质的方法。文献[6]利用断开相两端的电压大小来识别故障性质，但该方法不适用330 kV以上的输电线路。文献[7]利用瞬时性故障发生时断开相沿线各点的电压与电容耦合电压具有较小的相位差和幅值差的原理来识别故障，但其准确性易受到系统运行方式的负荷电流的影响。文献[8]利用人工智能中的神经网络来判断故障的性质，但其应用于自动重合闸领域需要大量的样本。文献[9]利用二次电弧反复熄灭与重燃所产生的高频信号来判定故障性质, 但该判据不仅需较高的采样频率与准确的电弧模型，而且计算量较大。

本文提出了一种基于短时傅里叶变换的单相自适应重合闸的方法，通过检测恢复电压阶段出现的拍频特性，利用短时傅里叶变换，求出变换后的频谱图，并根据起拍电压时刻出现的频率特性，识别出故障的性质。本文通过仿真研究，验证了该方法易于实现，简单可靠。

1 输电线路故障特性分析

1.1 电弧特性分析

输电线路发生故障时，由于系统与故障点之间仍然保持着联系，系统仍然对故障点处进行供电。

一次电弧是指输电线路发生瞬时故障开始到故障相断路器跳开的时间段内，电弧的弧长因系统的存在仍然保持稳定。一次电弧特性为

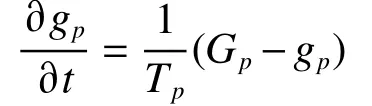
式中：gp为动态电导变量，Gp为稳态电导，Tp为时间常数。可得Gp为

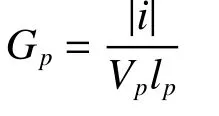
式中：|i|为电弧电流瞬时值的绝对值，Vp为单位长度电弧压降，lp为电弧弧长。时间常数Tp为

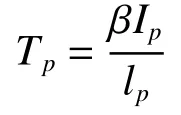
式中：比例系数 β约为2.85×10-5，Ip是电流峰值。通过实验研究表明，Vp在一个周期内基本保持稳定，且不受电弧电流变化的影响，在电弧电流1.4 ～24 kA时，电流的电位梯度为15V·cm-1，电弧电压梯度数值保持不变。

二次电弧是指线路中的断路器跳开，健全相依然运行，线路上由于健全相上的感应依然存在能量，导致电弧将会持续一段较长的时间，直到故障点处完全熄弧为止。二次电弧特性为

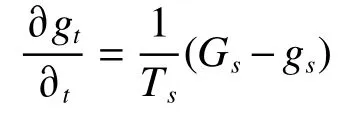
式中：gs是二次电弧时变电导，Gs是二次电弧的稳定电导，Ts是二次电弧时间常数。稳定电导为

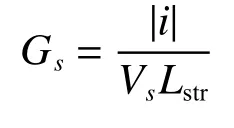
式中：Lstr为弧长，为电位梯度，|i|为 电流的绝对值，tr为电弧持续的时间长度。二次电弧的时间常数为

式中：α为二次电弧的比例常数，Is为电弧的电流峰值。

研究表明，在二次电弧阶段，电弧的熄灭、重燃与重燃电压值有着密切的联系。重燃电压的升高与二次电弧电流也有密切的联系，研究得到：

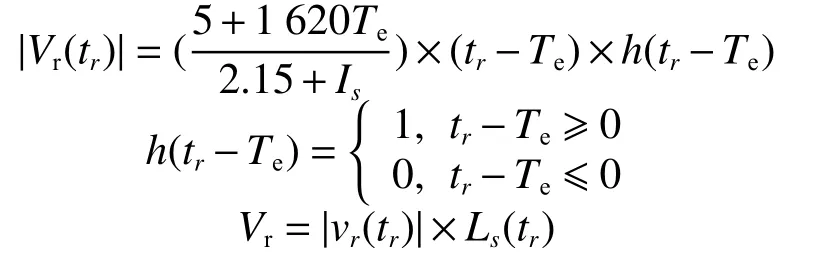
式中：|vr(tr)|为电位梯度，Te为电弧产生到完全熄灭所经历的时间，Vr为重燃电压。二次电弧重燃与熄灭的过程，使得电弧的长度随时间的变化不断的拉伸，从而导致故障相电压不断的上升[10]。随着时间的推移，二次电弧的重燃电压越来越高，此时二次电弧的电压始终无法大于重燃电压，真正达到熄弧状态，开始进入恢复电压状态。线路发生单相接地故障时，由于所处的环境开放，电弧燃烧过程中会受到多物理场等因素影响，例如风速、湿度、温度等。电弧燃烧过程中，温度对电弧的影响可以近似忽略，但空气中主要影响因素还是湿度与风速，所以根据电弧特性分析识别故障具有一定的难度与误差。

1.2 带并联电抗器的输电线路中恢复电压特性分析

线路发生故障时，线路两侧断路器跳开后，因电磁耦合和静电耦合作用产生的电弧称为潜供电流[11]。为了抑制潜供电流的出现，国内外专家学者提出了在线路两端安装并联电抗器的方法。其等效图如图1所示。

图1 双端安装并联电抗器的集中参数等效图

图1中的电抗器采用星网变换的连接方式转化为对角连接网形，并将其转换为相间耦合电容Cm的补偿电感Lm1、Lm2，将中性点电抗器转换为线路对地电容C0的补偿电感Lg1、Lg2，得到图2所示的等效电路。

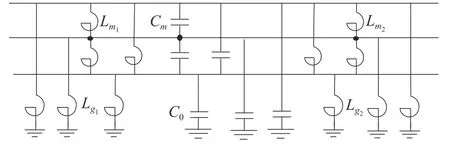
图2 对并联电抗器星网变换后的等效电路

图2中Lmk、Lnk和Lgk(k=1,2)关系为

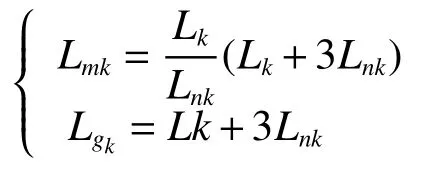
式中：k=1,2为组数，Lk为电感，Lnk为中性点小电感，Lmk为相间电感，Lgk为对地电感。

当瞬时性故障的二次电弧熄灭之后，线路的绝缘性恢复，线路开始进入恢复电压阶段，此时线路上存在故障相和健全相之间的电容耦合和电感耦合，因线路上并联电抗器的存在，电容、电感储能元件会产生自由振荡分量。其等效电路图如图3所示。

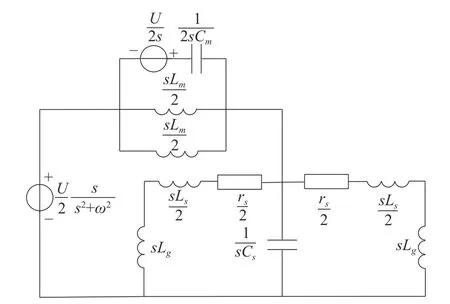
图3 复频域等效电路

由图3求得特征多项式：

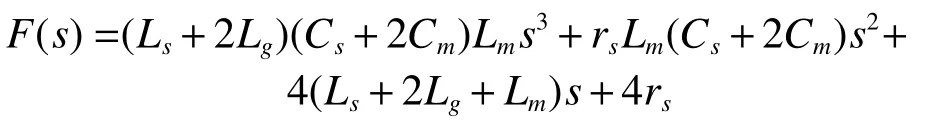
求解得自由震荡频率为

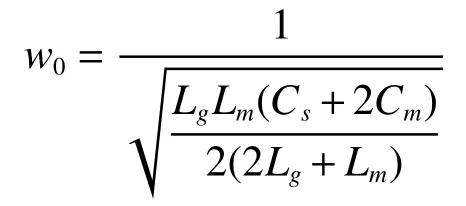
瞬时性故障时的自由分量为

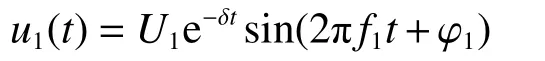
式中：U1为幅值，f1为频率，φ1为相位，δ为衰减系数。

瞬时性故障恢复阶段的工频分量为

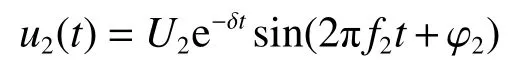
式中：U2为幅值，f2为频率，φ2为相位。

瞬时性故障恢复电压为

式中：

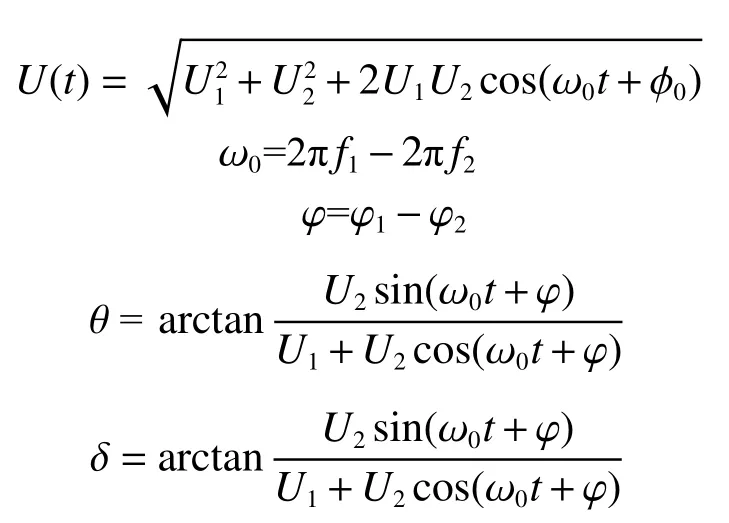
永久性故障恢复电压为

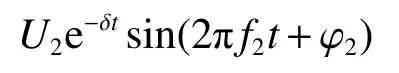
式中：U2为幅值，f2为频率， φ2为相位。

2 短时傅里叶变换

2.1 傅里叶变换

傅里叶变换算法是一种用于分析与合成信号的方法[12]，如果输入信号是一个只包含直流、整次谐波分量且不包括基频分量信号，则该输入信号的傅里叶变换将函数f(t)表示成复指数函数的积分形式，即

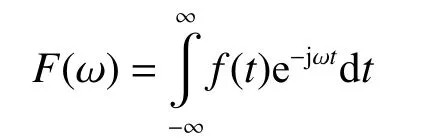
连续傅里叶变换的逆变换为

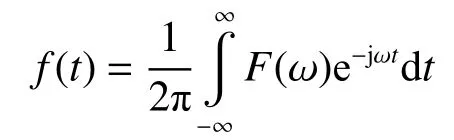
式中：f(t)为原函数，F(ω)为象函数。但传统的傅里叶变换仅仅捕获一段信号上所出现的频率成分，对各频率成分出现的具体时刻捕获不明显，且由于信号中带有的突变，傅里叶变换很难及时捕捉。针对上述情况的出现，短时傅里叶变换则很好地解决了这个问题。

2.2 STFT变换原理

若给定信号x(t)∈L2(R)为连续的时间信号，则短时傅里叶变换定义为

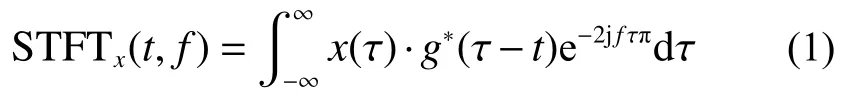
式中：g(τ)为窗函数，且‖g(τ)‖=1。

当给定信号为离散信号时，对连续信号进行采样，采样时间为Δt，则式(1)可表示为

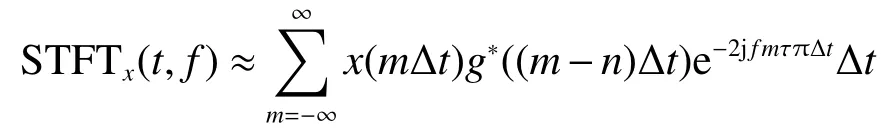
令x(n)=x(nΔt),ω=2πfΔt，则离散的傅里叶变换定义[13]为

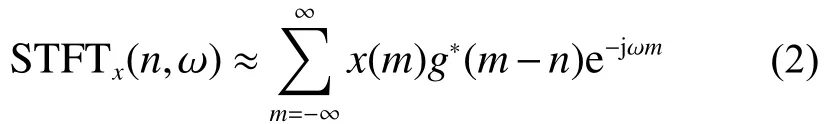
对式（2）等号两端分别取平方，可得：

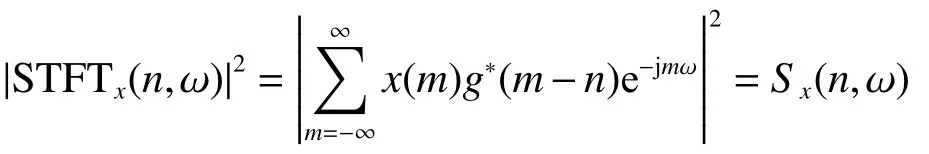
式中：Sx(n,ω)称为频谱图，表示信号能量的分布。

3 单相自适应重合闸拍频判据

3.1 拍频判据构成的原理

输电线路发生瞬时性故障时，因并联电抗器的存在会引起感性、容性元件之间形成自由震荡分量，继而产生电压拍频，但是发生永久性故障时却没有此故障[14]。从断路器断开时刻起，瞬时性故障会在电压起拍时刻处出现局部频率最大值，而永久性故障则不会出现局部频率最大值，且频率呈现出周期性规律。

3.2 自适应重合闸方案

自适应重合闸方案如图4所示，根据采集被保护输电线路MN故障相的电压值，对采集故障相电压进行归一化处理。当断路器断开后，用短时傅里叶变换来进行频谱的提取，通过观察提取出的频谱是否出现局部最大值且频率是否出现周期性规律来识别故障的性质。

4 仿真验证

为验证上述理论分析，本文采用EMTDC/PSCAD搭建550 kV带并联电抗器的输电线路仿真模型，仿真模型如图5所示。图5中，Δ/Y为Dy型变压器，MN段为输电线路，LMN=358km，AM段长度LAM=150km，NB段长度LNB=220km，并联电抗器电抗XL=1680.56Ω,Xn=434Ω。设采样频率为20kHz。

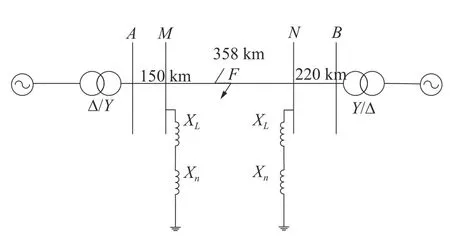
图5 双端安装并联电抗器的压输电线路示意

4.1 仿真案例1

设在线路MN上距M端100 km的F点处发生A相接地瞬时性故障，M端测得的故障相归一化后的电压波形如图6所示。

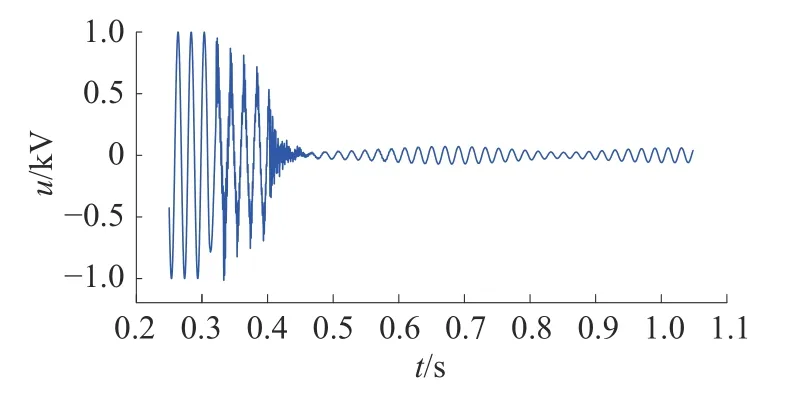
图6 距M端100 km处瞬时性故障归一化后的故障相电压波形

由图6可得故障发生时刻为0.314 s，断路器断开时刻为0.402 85 s，经过短时傅里叶变换后，得到频谱图7。

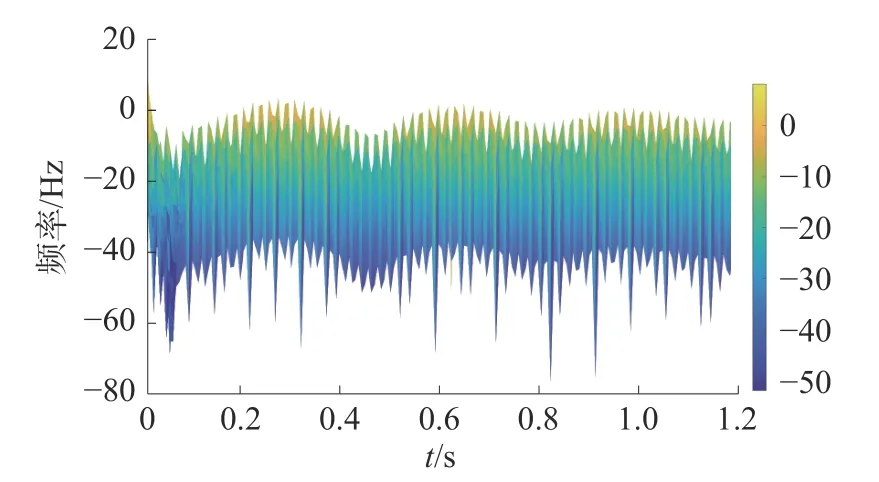
图7 距M端100 km处瞬时性故障波形频谱图

通过对频谱图7的分析，自断路器断开时刻起，在起拍电压0.82 s时刻处频率出现局部最大值，并且不呈现周期性规律，所以该故障为瞬时性故障。

设在线路MN上距M端100 km的F点处发生A相接地永久性故障，M端测得的故障相归一化后电压波形如图8所示。

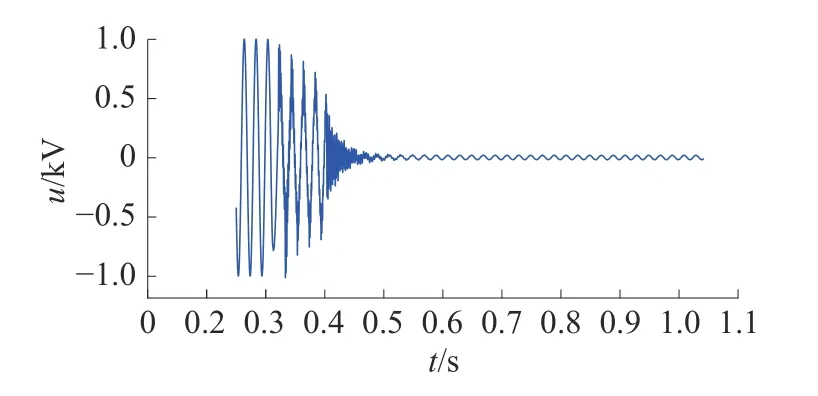
图8 距M端100 km处永久性故障归一化后的故障相电压波形

经过短时傅里叶变换后，得到频谱图如图9。

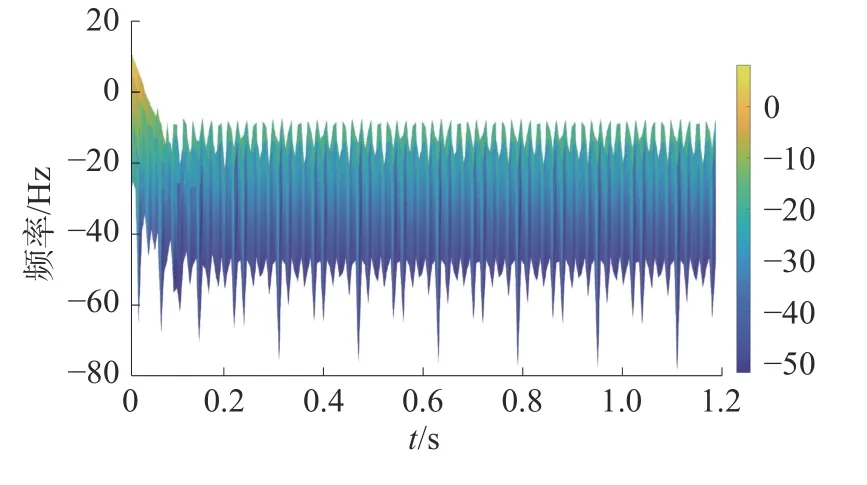
图9 距M端100 km处永久性故障波形频谱图

通过对频谱图9的分析，自断路器断开时刻起，频率未出现局部最大值，并且频率出现周期性的规律，所以该故障为永久性故障。

4.2 仿真案例2

设在线路MN上距M端150 km的F点处发生A相接地瞬时性故障，M端测得的故障相归一化后的电压波形如图10所示。

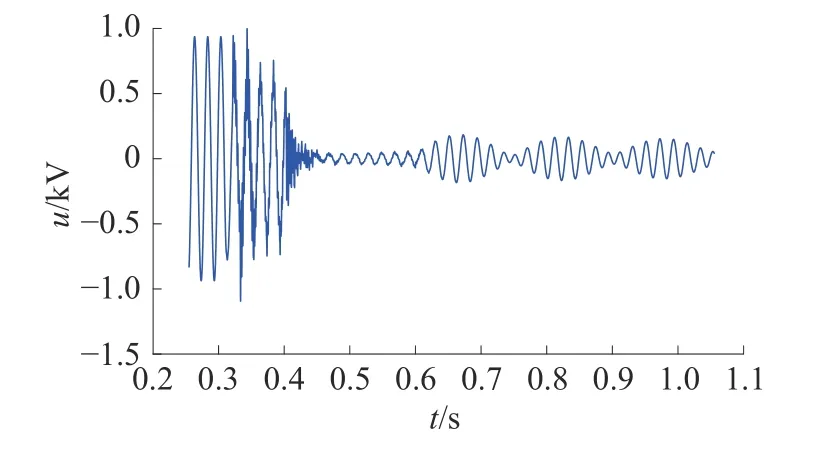
图10 距M端150 km处瞬时性故障归一化后的故障相电压波形

由图10可得故障发生时刻为0.326 s，断路器断开时刻为0.413 5 s，经过短时傅里叶变换后，得到频谱图如图11。

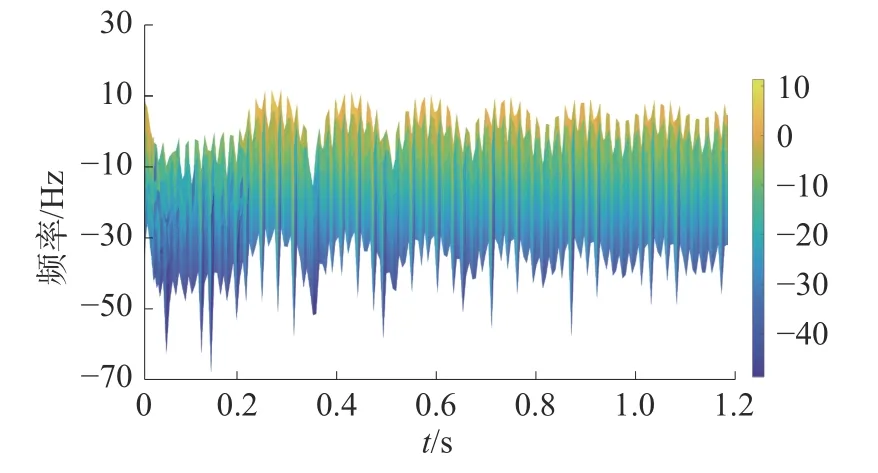
图11 距M端150 km处瞬时性故障波形频谱图

通过对频谱图11的分析，自断路器断开时刻起，在起拍电压0.87 s频率处出现局部最大值，并且不呈现周期性规律，所以该故障为瞬时性故障。

设在线路MN上距M端150 km的F点处发生A相接地永久性故障，M端测得的故障相归一化后电压波形如图12所示。

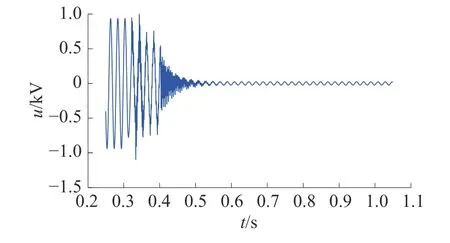
图12 距M端150 km处永久性故障归一化后的故障相电压波形

经过短时傅里叶变换后，得到频谱图如图13。

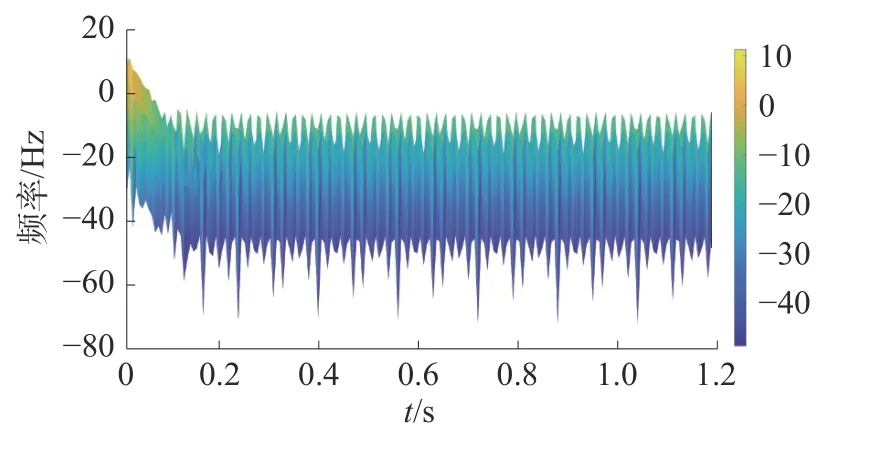
图13 距M端150 km处永久性故障波形频谱图

通过对频谱图13的分析，自断路器断开时刻起，频率未出现局部最大值，并且频率出现周期性的规律，所以该故障为永久性故障。

经过大量的仿真实验后得出的发生2种故障时仿真的数据如表1所示。

表1 仿真实验结果

5 结论

经过理论推导和仿真验证，在输电线路发生单相接地故障时，可利用在拍频现象中的起拍电压时刻处频率特性判断出故障的性质。本文提出的基于短时傅里叶变换的单相自适应重合闸的识别方法，能在重合闸前更好地判断当前线路的故障性质；若为瞬时 性故障，立即进行重合闸，恢复线路的供电；若为永久性故障，线路则不能进行合闸，实现自适应重合闸。