基于3维泊松点过程理论的无人机协助的异构网络模型及其性能
郭艺轩,贾向东,2*,曹胜男
(1.西北师范大学 计算机科学与工程学院,甘肃 兰州 730070;2.南京邮电大学 江苏无线通信重点实验室,江苏 南京 210003)
第5代(fifth generation, 简称5G)移动通信使终端量和数据量急剧增长,增加频带资源和扩大基站密度能适应此变化.异构网络(heterogeneous network, 简称HetNet)是5G的核心架构,通过部署密集小基站扩大网络覆盖概率,从而提高网络容量[1-2].传统的小基站不够灵活,在紧急热点场景具有局限性.无人机基站(drone-base station, 简称D-BS)具有灵活及易部署的优点,可用于第6代(sixth generation, 简称6G)移动通信网络[3-4],因此无人机网络成为研究热点.文献[5]研究了移动状态下地面用户的接收速率.文献[6]研究了移动状态下无人机网络的切换概率.文献[5-6]均根据2维泊松点过程(two-dimensional Poisson point process, 简称2-D PPP)理论对D-BS的位置建模,假设用户周围存在局部散射、信道为瑞利信道.文献[7]根据二项点过程理论对D-BS的位置建模,假设信道衰落为Nakagami-m衰落,对地面参考接收机的下行链路覆盖概率进行研究.文献[8]研究了无人机协助的多层HetNet的吞吐量,使用泊松簇过程理论描述D-BS的分布,根据泊松点过程(Poisson point process, 简称PPP)理论对地面基站(ground-base station, 简称G-BS)的位置建模.文献[9]根据Matérn硬核点过程理论对D-BS的位置建模,将下行链路信道建模为符合Nakagami-m衰落规律的毫米波信道,对不同系统参数下的保密率进行了研究.文献[10]根据无限平面上的PPP(Poisson point process)及有限圆区域的二项点过程理论,对由G-BS和D-BS组成的双层异构网络建模,采用视距(line of sight, 简称LoS)和非视距(not line of sight, 简称NLoS)传播模型分析覆盖概率和频谱效率.文献[11]根据二项点过程理论对D-BS的位置建模,假设信道衰落为莱斯衰落.文献[12]根据齐次PPP及Matérn硬核点过程理论分别对D-BS及地面用户设备(ground user equipment, 简称GUE)的位置建模,假设D-BS在Sub-6 Ghz和mm-Wave双频段下部署,该部署能满足网络服务质量要求.
上述文献均在固定高度的2维平面对D-BS的位置建模,未考虑D-BS的高度,使这些方案不能适用于无人机服务的热点场景.针对该问题,文献[13]根据Matérn硬核点过程理论对HetNet中所有制式基站的位置建模,研究了覆盖概率.文献[14]提出了一种混合移动模型,研究了3维动态D-BS的覆盖概率,但未考虑D-BS的位置分布.文献[15]根据3维泊松点过程(three-dimensional Poisson point process, 简称3-D PPP)理论对同一类型基站的位置建模,分析了覆盖概率和传输速率.文献[16]基于2维随机几何理论对大规模多输入多输出中继异构网络的频谱效率进行了研究.文献[17]为了提高HetNet的性能,基于PPP提出了一种非正交多址接入的双连接异构网络模型.然而,文献[16-17]的网络模型均只考虑了简单2维情况,未研究复杂的3维情况.针对紧急热点场景,该文拟提出基于3维泊松点过程理论的无人机异构网络模型,仿真分析性能参数间的关系.
1 基于3维泊松点过程的无人机异构网络模型
宏基站出现故障或者吞吐量需求较高导致传统位置固定的小基站不能满足应急需求时,可部署载有通信收发装置的无人机应急组网,以解燃眉之急.图1为该文提出的基于3维泊松点过程理论的无人机异构网络模型结构.
根据3-D PPP理论对D-BS的位置建模.构建混合双层的HetNet.假设在有限3维空间有多个无人机作为空中小基站,其分布遵循密度为λD的3-D PPP;G-BS作为宏基站,其分布遵循密度为λG的2-D PPP.由于无人机可通过调整位置形成较有利的空对地信道,因此将信道建模为LoS链路[18].将小尺度衰落设为瑞利衰落[19].信干噪比(signal to interference plus noise ratio,简称SINR)定义式为
(1)
其中:n=D,G(D为无人机基站,G为地面基站);x为GUE与通信基站的距离;I为其他所有制式基站的总干扰;Pn为通信基站的发射功率;αn为路径损耗;g为信道增益;σ2为归一化的加性噪声功率.
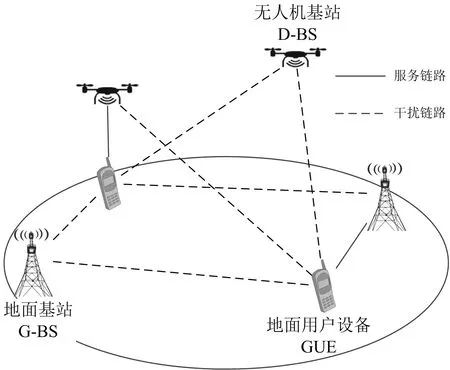
图1 基于3维泊松点过程的无人机异构网络模型结构
2 性能参数
2.1 级联概率
假设GUE根据最大接收功率级联准则选择服务基站进行通信[20-21].当GUE与D-BS通信时,两者的级联概率表达式为
(2)
其中:E(·) 为数学期望函数;P(·)为概率函数;PD,PG分别为GUE与最近的D-BS,G-BS通信时的接收功率;PD,PG分别为GUE与最近的D-BS,G-BS的发射功率;RD为GUE与最近D-BS的距离,RG为GUE与最近G-BS的距离.
根据2-D PPP的空概率性质,有
(3)
根据3-D PPP理论,D-BS与GUE距离的概率密度函数(probability density function, 简称PDF)的表达式为
(4)
将式(4)代入式(2),得到GUE与D-BS的级联概率表达式为
(5)
同理,可得GUE与G-BS的级联概率表达式为
(6)
2.2 用户与通信基站距离的分布函数
当用户与D-BS通信时,两者距离XD的互补累积分布函数(complementary cumulative distribution function, 简称 CCDF)表达式为
(7)
根据最大接收功率级联准则,式(7)中的分子可表示为
(8)
式(8)可改写为
(9)
将式(9)代入式(7),可得XD的CCDF为
(10)
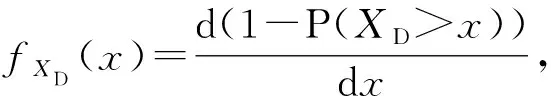

(11)
同理,当GUE与D-BS通信时,两者距离XG的PDF表达式为
(12)
2.3 下行链路的覆盖概率
GUE与D-BS通信时的下行链路覆盖概率为
(13)
其中
(14)

(15)
根据干扰功率I的拉斯变换(Laplace transform, 简称LT), 式(15)可简化为
(16)

(17)
其中:y为干扰基站与GUE的距离;Φ′D,Φ′G分别为D-BS,G-BS的干扰信号集合.结合式(16),(17),可得GUE与D-BS通信时的下行链路覆盖概率为
(18)
同理, GUE与G-BS通信时的下行链路覆盖概率为
(19)
综上,该网络下行链路的总覆盖概率为
(20)
2.4 下行链路的频谱效率
GUE与D-BS通信时的下行链路频谱效率为

(21)
其中

(22)
(23)
将式(23)代入式(21),可得GUE与D-BS通信时的下行链路频谱效率为
(24)
同理, GUE与G-BS通信时的下行链路频谱效率为
(25)
综上,该网络下行链路的总频谱效率为
SE=SEDAD+SEGAG.
(26)
3 仿真分析
使用MATLAB对网络模型性能参数间的关系进行定量分析.假设:双层HetNet为半径1 km的球形区域; D-BS分布遵循密度λD=10-5个·m-3的3-D PPP,G-BS分布遵循密度λG=5×10-6个·m-3的2-D PPP;G-BS,D-BS的发射功率分别为50,30 dBm;G-BS的路径损耗αG为3,D-BS的路径损耗αD为4;噪声功率σ2为-104 dBm;SINR阈值范围为-20~20 dB.
图2为基站密度与级联概率的关系曲线.由图2可知,D-BS密度越大,GUE与D-BS的级联概率AD越大;G-BS密度越大,GUE与G-BS的级联概率AG越小;αD变大使AD变小、AG变大.
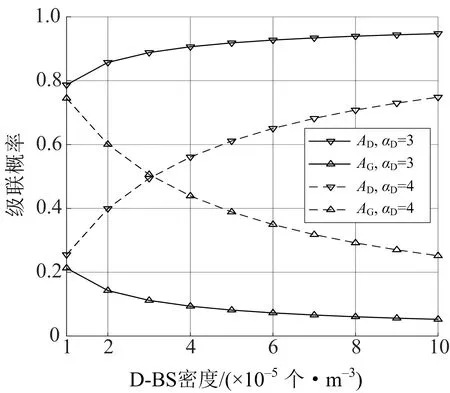
图2 基站密度与级联概率的关系曲线
图3为不同网络模型的下行链路总覆盖概率,图3中,2D模型的所有基站均为2D分布;3D模型的所有基站均为2D分布;该文模型的G-BS为2D分布,D-BS为3D分布.由图3可知,随着SINR阈值的增加,所有模型的下行链路总覆盖概率均减小;相对于2D,3D模型,该文模型的总覆盖概率曲线与实际分布的总覆盖概率曲线靠得最近,表明该文模型能更精准地描述覆盖概率.
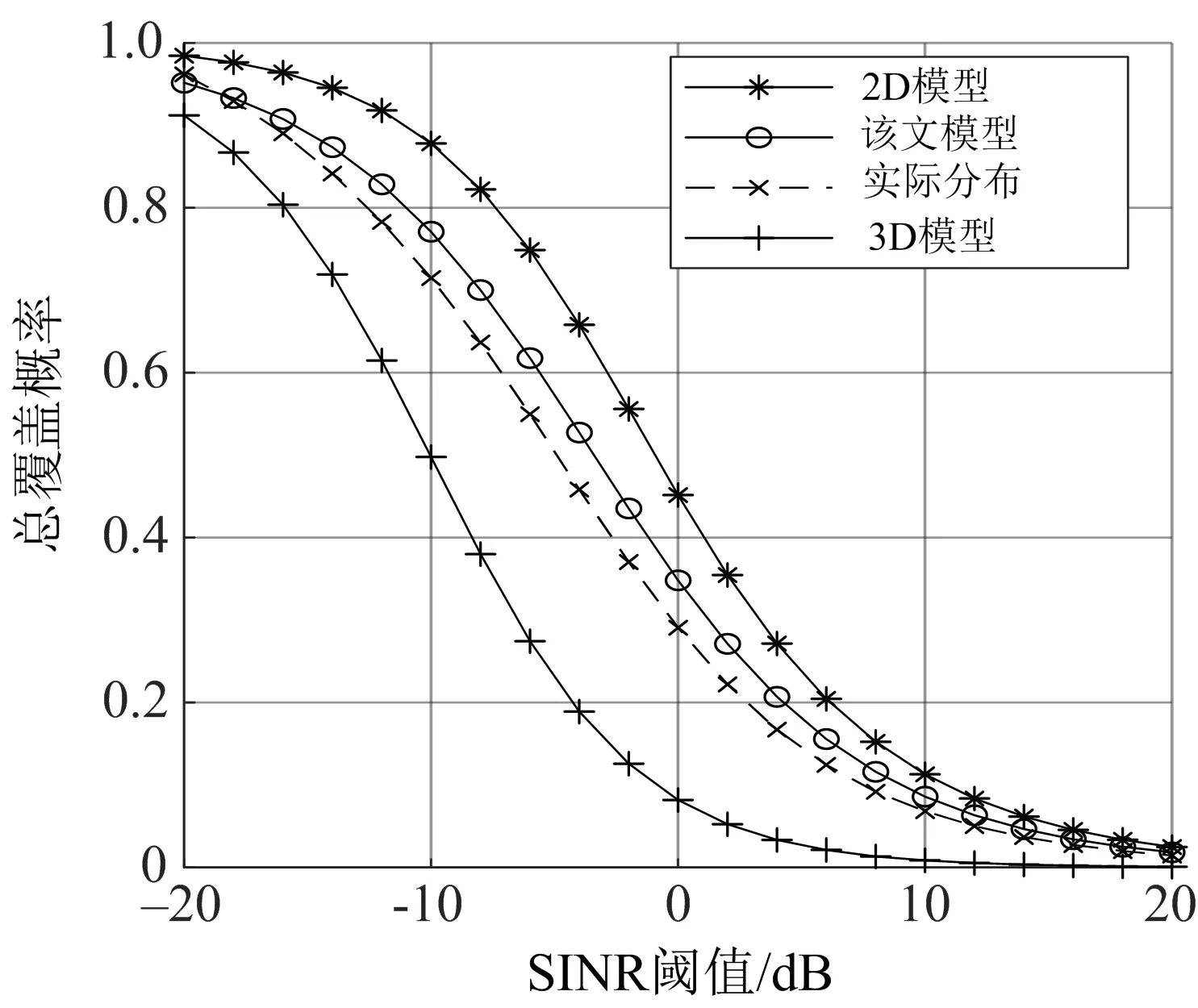
图3 不同网络模型的下行链路总覆盖概率
图4为D-BS发射功率PD与下行链路覆盖概率的关系曲线.由图4可知,SINR阈值γ不变时,增加PD能提高D-BS的覆盖概率、降低G-BS的覆盖概率.因此,使用多个低功率的无人机小基站协助G-BS通信,能改善整个网络的覆盖性能.

图4 D-BS发射功率与下行链路覆盖概率的关系曲线
图5为该文网络模型的D-BS路径损耗与下行链路总覆盖概率的关系曲线.由图5可知,仿真值曲线与理论值曲线基本吻合;覆盖概率对SINR阈值γ的变化非常敏感;覆盖概率随路径损耗的增加而增加,最后趋于平稳.因此,路径损耗增加使总覆盖概率增加,但路径损耗增大到一定值后,对总覆盖概率的影响逐渐减小.

图5 D-BS路径损耗与下行链路总覆盖概率的关系曲线
图6为该文网络模型的D-BS密度与下行链路的总频谱效率的关系曲线.由图6可知,αG不变时,频谱效率随αD增加而增加;αD>αG时,频谱效率随D-BS密度λD的增加而增加;αD≤αG时,频谱效率随D-BS密度λD增加而减小.因此,部署网络时需对路径损耗做适当选择.
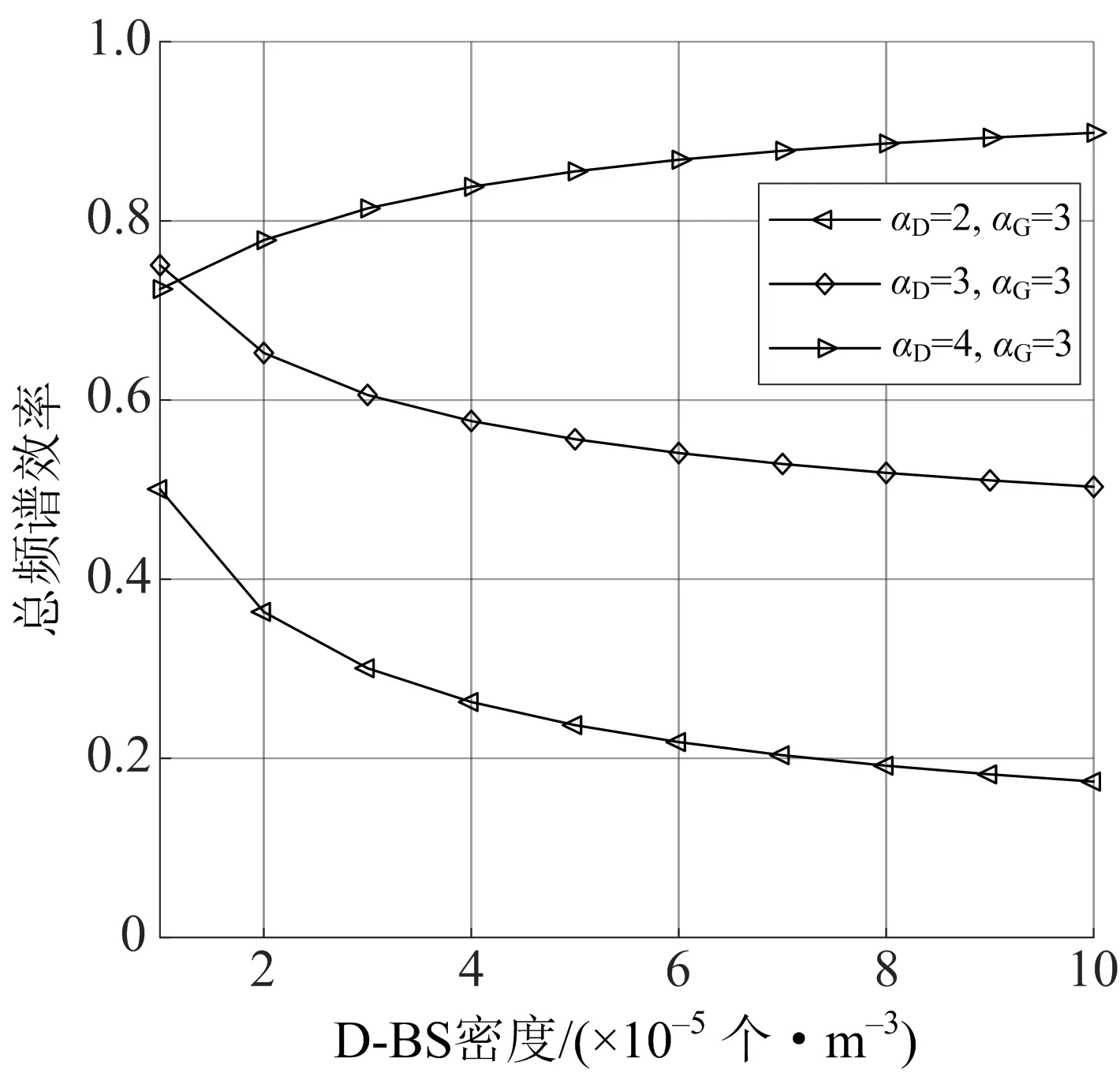
图6 D-BS密度与下行链路的总频谱效率的关系曲线
4 结束语
该文提出了基于3维泊松点过程理论的无人机异构网络模型.仿真分析相关参数对覆盖概率和频谱效率的影响.仿真结果表明:相对于2D,3D模型,该文模型能更精准地描述覆盖概率;使用多个低功率的无人机小基站协助G-BS通信,能改善整个网络的覆盖性能;部署网络时需对路径损耗做适当选择.异构网络的频谱分配将为后续研究内容.

