基于STUR收获机组适宜作业单元地块长度和面积耦合关系研究
乔金友,李 荣,张朋永,万盈贝,陈海涛,李文华
(1.东北农业大学工程学院,哈尔滨 150030;2.哈尔滨航天恒星数据系统科技有限公司,哈尔滨 150010;3.黑龙江省农业科学院,哈尔滨 150086)
2020年全国综合农业机械化程度达到71.25%,我国农业机械化已进入高级阶段[1-2]。但农业机械化发展过程中仍存在一系列问题,其中,农业机组技术参数与作业单元地块条件参数间无定量匹配关系[3],农业动力机械结构不合理、农业机械化发展不平衡[4-5]等问题突出。针对现阶段耕地细碎化现状[6],研究作业单元地块大小与农业机组作业时间利用率等参数间定量匹配关系,为不同规模条件下农业机械选型提供理论基础,促进农机动力结构合理化,助力农业机械化向质量效益型转变。
时间利用率、地块条件参数等指标是影响农业机组作业效率重要因素[7],国内外学者在此方面研究较多。Henning 等建立非线性规划模型研究地块大小、作业时间等参数对农机作业效率的影响[8];Hameed等建立包括作业时间和地头长度、地块面积等参数仿真模型,应用该模型可使机组作业时间减少4.5%、作业效率提高6.6%[9];Sopegno等建立基于多田、多作物生产系统的农机作业成本预测模型,考虑作业时间和作业面积等影响因素对作业成本的影响[10]。Janulevicius等采用160 kW拖拉机组进行土壤翻耕作业,结果表明时间利用率与地块长度呈非线性关系变化[11]。
国内对农业机组时间利用率研究较早。20 世纪60 年代,北京农业机械化学院测定分析主要作业机组班次时间利用率,为后续研究奠定基础[12]。杜兵依据耕、耙、播、收4 种农业机组的工作日志,划分机组班时间构成项目,得到各项目时间所占比率[13]。陈丽能等研究结果表明作业单元地块长度较短时,农业机组机械能得不到充分利用、生产率低[14]。孔德刚等分析大功率拖拉机播种作业时间和作业效率,并指出拖拉机播种作业过程中辅助作业时间长、拖拉机与播种机性能匹配不当等问题,并提出提高机组作业效率的建议[15]。罗丹等采用40 马力拖拉机悬挂三铧犁在长宽比为4:1作业单元地块上耕作,得到机组时间利用率随作业单元地块面积增大而增大的规律[16]。乔金友等建立不同机组时间利用率计算模型,通过试验获取机组各项作业时间数据,得到不同作业单元地块长度条件下机组作业时间利用率或技术生产率随作业单元地块面积变化的规律[17-18]。刘玉等针对耕作单元细碎化现状,利用曲线拟合方法得到小麦机收时间随作业单元地块面积增加而增加[19]。郑大明通过试验得到插秧机各项作业时间,建立插秧机时间利用率和技术生产率模型,研究得到插秧机组时间利用率随作业单元地块长度和面积变化关系[20]。
综上,关于农业机组作业时间利用率等参数与作业单元地块条件参数关系方面研究受到国内外专家广泛关注,大多学者建立农业机组作业效率、时间利用率数学模型,通过试验、数据计算等方式分析农业机组作业时间利用率和作业效率与地块参数间的关系,研究证明农业机组作业时间利用率、技术生产率等参数与作业单元地块面积、地块长度等因素关系密切。但目前研究成果仍不能清晰表达机组作业时间利用率与作业单元地块条件间确定的定量关系。因此,建立机组时间利用率随作业单元地块条件变化关系的通用数学模型,研究目标时间利用率条件下机组适宜的作业单元地块长度与地块面积定量耦合关系,不仅可完善农机运用相关理论,同时可为农业生产者依据土地规模选择合适的农业机组提供直接指导,具有重要理论和实践意义。
1 机组STUR 概念及其与作业单元地块条件关系模型建立
1.1 机组作业季节时间利用率(STUR)概念界定
因农业机组作业过程中故障停歇时间、组织不当停歇时间等发生频率较低,若仅以机组作业班次时间为研究对象可能致使机组作业时间利用率计算结果出现偏差,导致研究结果和结论失真。以机组作业季节为测定周期,研究时间利用率与作业单元地块条件间变化关系可避免上述问题。因此提出农业机组作业季节时间利用率(STUR)概念。
定义:农业机组作业季节时间利用率(Season time utilization rate,STUR)为农业机组整个作业季节纯作业时间与该机组作业季节总出勤时间比值。计算模型如式(1)所示。
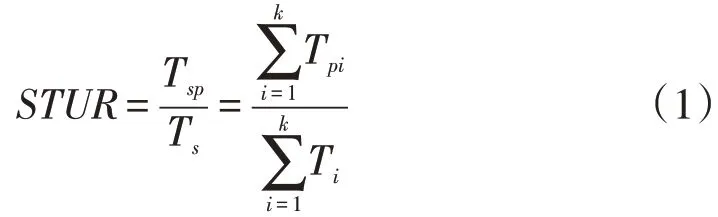
式中,STUR 为农业机组作业季节时间利用率(%);Tsp为作业季节内机组纯作业时间(s);Ts为机组作业季节内总出勤时间(s);Tpi为机组完成第i个作业单元地块的纯作业时间(s);Ti为机组完成第i个作业单元地块作业总时间(s);k为作业季节机组完成的作业单元地块数。
1.2 收获机组STUR 随作业单元地块条件变化关系模型建立
①作业单元地块条件参数选择
由于实施联产承包责任制,许多自然地块被划分为多个作业单元地块。作业单元地块多为矩形,一般采用地块面积、地块长度、地块宽度或长宽比等作为矩形地块特征参数。而地块宽度是地块面积与长度之比,因此选用地块面积和地块长度作为作业单元地块条件特征参数具有代表性。
②收获机组STUR随作业单元地块条件变化的一般模型
鉴于上述思想,建立收获机组在矩形地块中以单侧卸粮方式作业时,STUR 随作业单元地块长度及面积两个参数变化关系模型如式(2)所示。
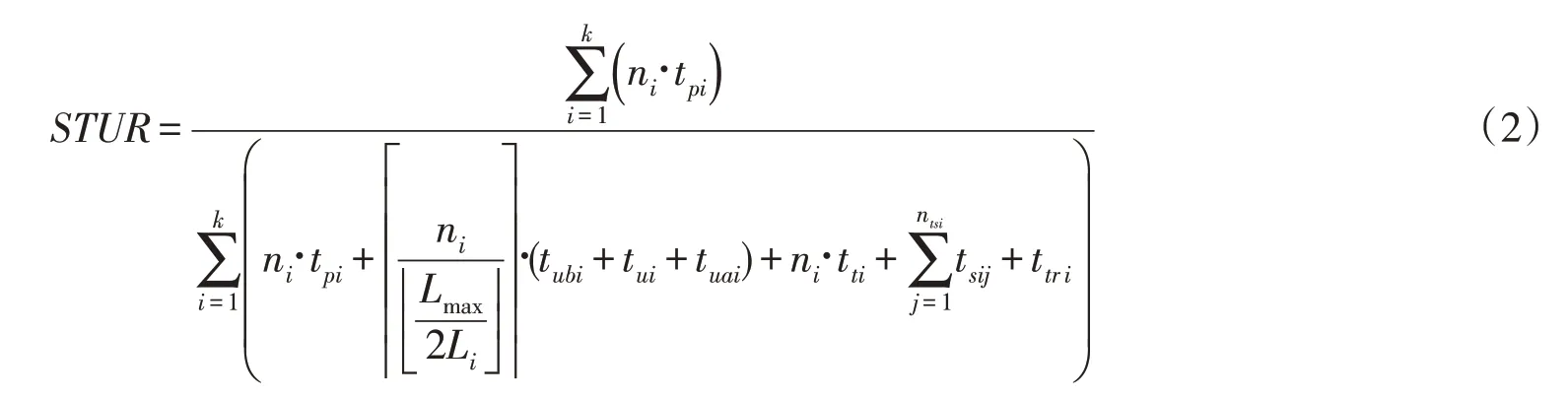
式(2)中,ni为收获机组完成整块地时作业行程数量;tpi为机组完成第i 个作业单元地块作业单个行程纯作业时间(s);Li为第i个作业单元地块长度(m);Lmax为收获机作业最大距离(m);tubi为第i个作业单元地块平均单次卸粮准备时间(s);tui为第i个作业单元地块平均单次卸粮时间(s);tuai为第i 个作业单元地块卸粮后平均准备进地时间(s);tti为机组在第i个作业单元地块上工作时平均单次转弯时间(s);tsij为机组完成第i 个作业单元地块第j次停歇时间(s);ttri为收获机组从第i作业单元地块到第i+1地块转移时间(s);k为作业季节内机组完成作业单元地块数;ntsi为机组完成第i作业单元地块作业停歇次数。
③收获机组STUR随作业单元地块条件变化的模型改进
式(2)分母包括作业单元地块长度Li,虽在一定程度上可表述机组STUR 与作业单元地块条件。但因式中单行程纯作业时间tpi、完成第i 作业单元地块作业行程数ni等也为地块长度、地块面积的函数,所以采用式(2)不能清晰表达收获机组STUR与作业单元地块条件间的关系。
由于机组完成第i 作业单元地块作业行程数ni是作业单元地块宽度与机组作业幅宽之比,而作业单元地块宽度为地块面积与地块长度之比,所以可采用式(3)计算机组作业行程数ni。

式(3)中,Si为第i个作业单元地块的作业面积(hm2);Bp为收获机组作业幅宽(m)。式(3)为作业行程数与作业单元地块面积、地块长度关系模型。
机组完成一个行程的作业过程包括进出行程的加减速过程和行程中的匀速作业过程,则农业机组单行程纯作业时间tpi可采用式(4)计算。
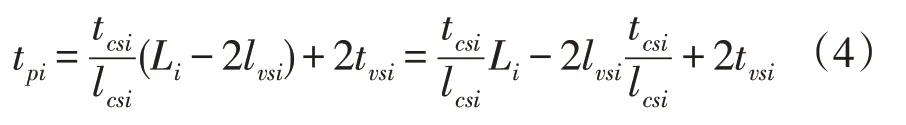
式(4)中,tcsi为收获机组完成第i个作业单元地块单行程中匀速作业时间(s);lcsi为机组完成第i个作业单元地块单行程中匀速作业距离(m);lvsi为机组完成第i个作业单元地块单行程加速或减速作业距离(m);tvsi为收获机组完成第i 个单元地块作业进入或离开行程加速或减速作业时间(s)。式(4)为单行程纯作业时间与作业单元地块长度关系模型。
将式(3)和式(4)分别代入式(2)可得收获机组STUR 与作业单元地块条件间的关系的改进模型如式(5)所示。

由式(5)可知,收获机组STUR 与作业单元地块面积、地块长度、机组作业幅宽、收满箱粮的最大作业距离以及各项时间等参数有关。在测试方案确定情况下,lcsi和lvsi为固定值,作业过程中发生的各项时间亦可测得;在机组类型及作业项目确定条件下,机组作业幅宽和作业速度为固定值。
依此可设如下常量:
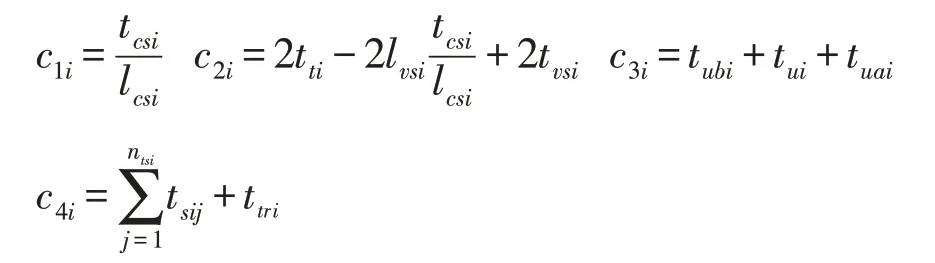
则式(5)变为:
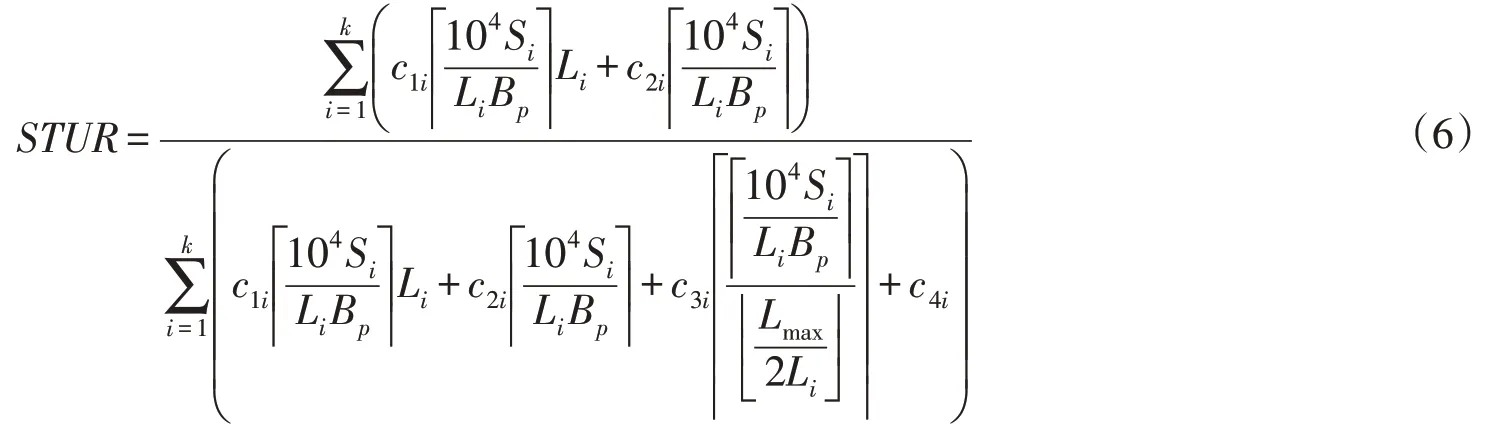
与式(2)或(5)相比,式(6)中变量仅有作业单元地块面积和地块长度,机组作业幅宽取决于播种机结构参数,其他参数均为常量或可通过试验测得,式(6)更直观、清晰表达收获机组STUR与作业单元地块条件关系,为计算收获机组STUR通用模型。
2 收获机组STUR 与作业单元地块条件关系分析
2.1 收获机组选择与数据获取
选择生产中常用大、中、小3种型号联合收获机组为研究对象,各机组基本技术参数见表1。
依据文献[17],当取收获机组单行程作业加减速距离lvsi为10 m,测试匀速作业距离lcsi为100 m时,测得各机组收获大豆时的各项时间数据见表2。
2.2 收获机组STUR 随作业单元地块条件变化趋势
依据表1 各机型相关参数和表2 各时间项目数据,可计算式(6)中各常量值;结合生产实际,取作业单元地块长度范围为200~1 600 m、步长200 m,作业单元地块面积范围为0.5~10 hm2、步长0.5 hm2,采用Matlab2020b 编制程序分别计算不同作业单元地块长度和地块面积条件下各收获机组STUR,绘制不同作业单元地块长度条件下各收获机组STUR随作业单元地块面积变化散点图,如图1 所示。为更清晰表达机组STUR 随作业单元地块面积的变化趋势,图1仅给出作业单元地块长度为200、400、600和800 m 4组数据散点图,当作业单元地块长度取其他值时,变化趋势与图1相同。

表1 三种收获机组基本参数Table 1 Basic parameters of 3 kinds of combine harvester

表2 收获机组作业时间测试数据Table 2 Tested time data of combine harvesters
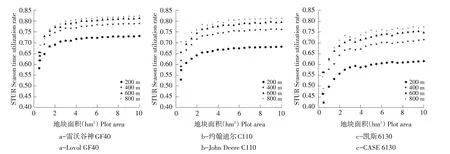
图1 收获机组STUR随作业单元地块长度和面积变化散点图Fig.1 Scatter diagram of combine harvesters STUR varies with plot length and area
由图1 可知,3 种收获机组STUR 随作业单元地块面积变化趋势相似:当作业单元地块长度一定时,STUR随作业单元地块面积增加而增大,其增加速率先快后慢;当作业单元地块面积不变时,STUR随作业单元地块长度增加而增大,其增加速率亦呈先快后慢趋势。
2.3 收获机组STUR 随作业单元地块面积变化规律回归模型
图1 表示收获机组STUR 随作业单元地块条件参数变化离散趋势,无法反映其连续变化定量规律。因此,需对各作业单元地块长度条件下STUR与作业单元地块面积数据进行非线性回归,以分析STUR随作业单元地块条件参数连续变化规律。
根据图1 收获机组STUR 随作业单元地块面积变化趋势可排除线性、二次曲线和三次曲线等函数关系,选择逆函数、对数函数、幂函数、复合函数、增长函数、指数函数和Logistic 曲线7 种预选模型,采用SPSS 24.0 对3 种收获机组在不同作业单元地块长度条件下STUR随作业单元地块面积变化规律进行非线性回归,回归模型及其相关参数如表3所示。受篇幅限制,仅列出作业单元地块长度为200 m 时,收获机组STUR 随作业单元地块面积变化的各种回归模型及相关参数。
根据以下3条原则选择最优拟合模型[21]:
①考虑实际问题特点,STUR、作业单元地块面积不能为负值,且STUR取值范围为(0,1);
②取检验水平α=0.01,通过F 检验的预选模型为有效模型;
③在通过F 检验的有效回归模型中,选择决定系数R2最大的模型为最优模型。
由表3可知,不同作业单元地块长度条件下,3种收获机组STUR随作业单元地块面积变化的各回归模型F值和R2值规律一致,可采用同一类回归模型表达收获机组STUR随作业单元地块面积变化规律。
依据上述原则,表3中各回归方程F值均大于F0.01=8.29,均为有效模型。其中,逆函数回归模型决定系数R2最大,为理论最优模型,但当作业单元地块面积较小时,采用此回归模型计算的STUR为负值,与上述原则①矛盾,因此无法选择逆函数。在剩余模型中选择R2值最大的对数函数表示不同作业单元地块长度条件下各机型STUR与作业单元地块面积函数变化模型。在不同作业单元地块长度下3 种收获机组STUR 随作业单元地块面积变化具体模型及相关参数如表4所示。
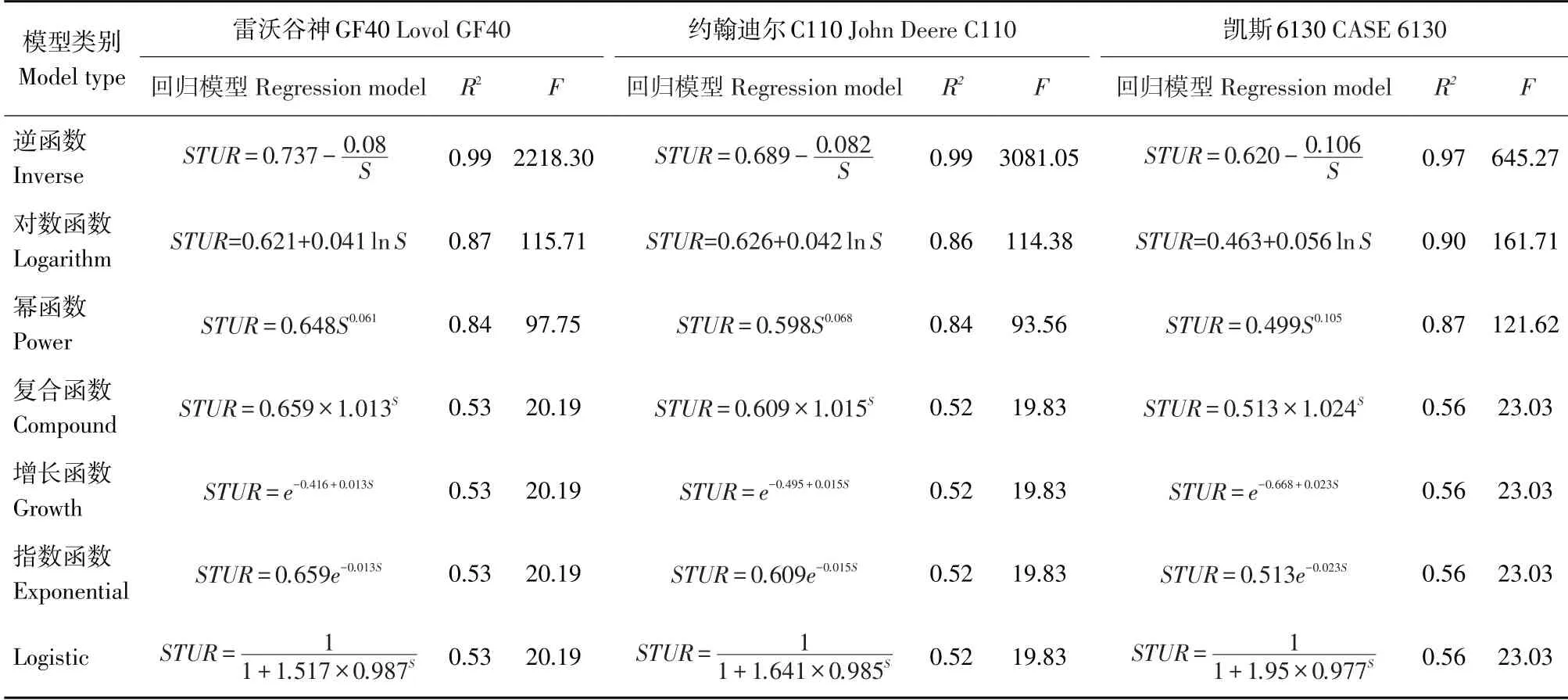
表3 收获机组STUR回归模型及其相关参数Table 3 Regression models and relevant coefficients of STUR varies with plot area
表4给出8种作业单元地块长度条件下,不同功率收获机组STUR 与作业单元地块面积间呈对数函数变化,反映收获机组STUR与作业单元地块面积间定量规律。在特定作业单元地块长度和给定目标STUR 条件下,依据表4 给出的定量变化关系可求得收获机组适宜的作业单元地块面积;也可计算机组在一定作业单元地块条件下作业时STUR。
因表4中仅包含部分作业单元地块长度条件下回归模型,仅支持有限的作业单元地块长度条件下机组选型,无法直接给出相应机组适宜的所有作业单元地块条件和根据各种作业单元地块选择适合的机组类别与型号。因此,表4中模型不具有广泛代表性,无法作为不同作业单元地块条件与不同机型间匹配关系直接依据,仍需作进一步分析处理。
3 收获机组适宜作业单元地块长度和面积耦合关系及应用
3.1 基于目标STUR 收获机组适宜作业单元地块长度和面积耦合模型建立
依据调研获得收获机组实际作业时间利用率,确定目标STUR分别为0.6、0.7、0.8时,利用非线性回归拟合得到收获机组适宜的作业单元地块长度和面积耦合关系。
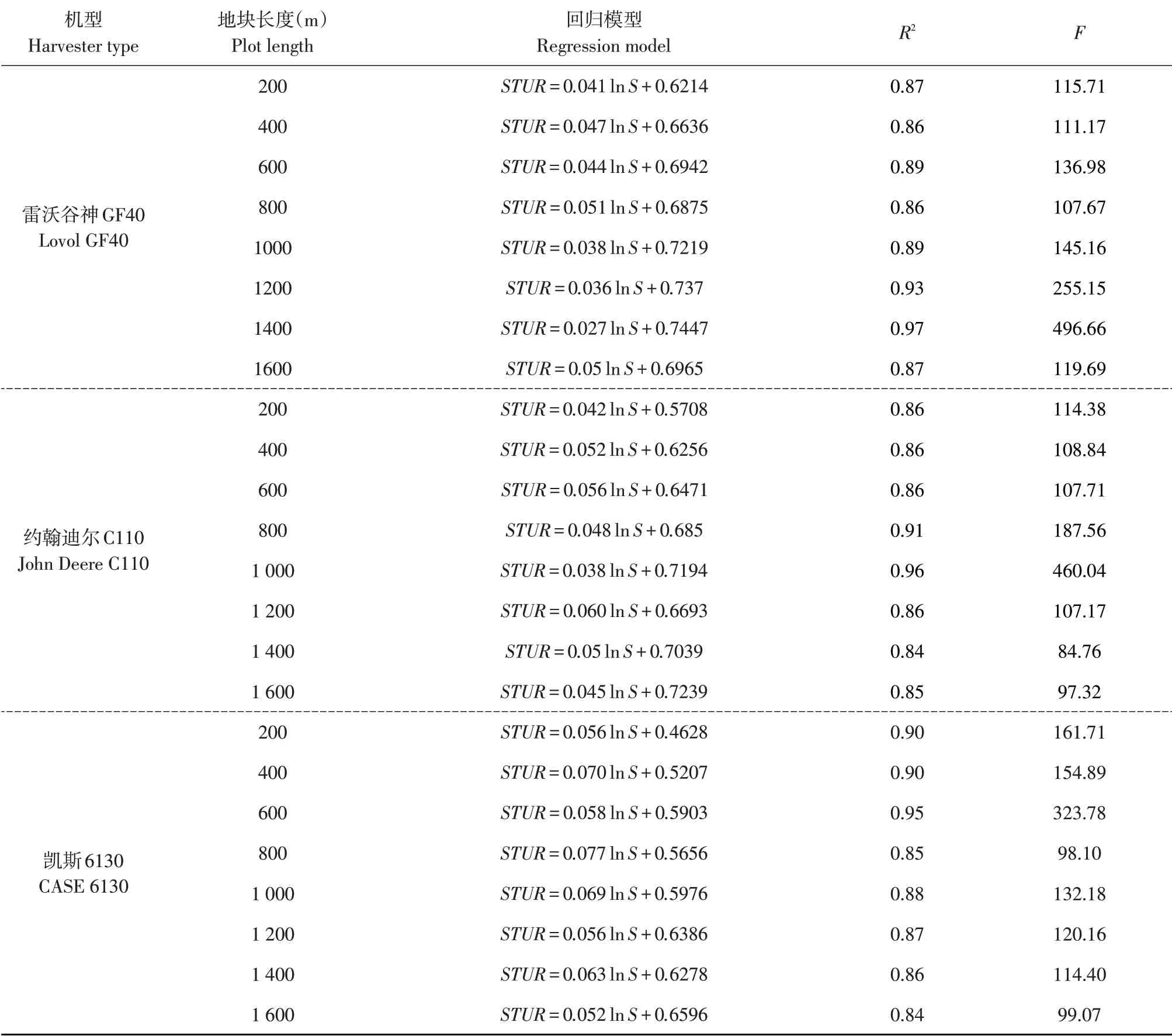
表4 不同作业单元地块长度收获机组STUR随地块面积变化回归模型Table 4 Regression models of combine harvesters'STUR varies with plot area
依据表4 中回归模型,分别计算当STUR 取0.6、0.7和0.8,作业单元地块长度为200~1 600 m、步长为10 m 时,各收获机组适宜的作业单元地块面积,并绘制机组特定STUR条件下作业单元地块长度与面积耦合关系散点图(见图2)。依据散点分布情况及变化趋势,结合前述原理采用SPSS 24.0进行非线性回归,依据最优回归模型选择原则得到幂函数模型不但通过F检验(F0.01=8.29)、满足实际问题要求,且决定系数R2最大(均大于0.87)。因此,确定幂函数为收获机组适宜作业单元地块长度和面积最佳耦合模型。当STUR 分别为0.6、0.7、0.8 时,3 种机组适宜作业单元地块长度与地块面积定量耦合关系曲线及其相关参数如图2 所示。确定STUR 条件下,3 种收获机组适宜的作业单元地块面积随地块长度增加而减少;且当作业单元地块长度一定时,增大作业单元地块面积可提高机组STUR;当作业单元地块面积一定时,增加作业单元地块长度也增加机组STUR,结论与罗丹等研究结果一致[16-17,19]。原因是当作业单元地块长度一定时,地块面积增加使机组作业季节内作业地块数量减少,进而减少地块转移次数,地块转移时间减小,STUR 增加;当作业单元地块面积一定时,地块长度增加,机组在地块内转弯次数减少,转弯时间减少也致使机组STUR增加。
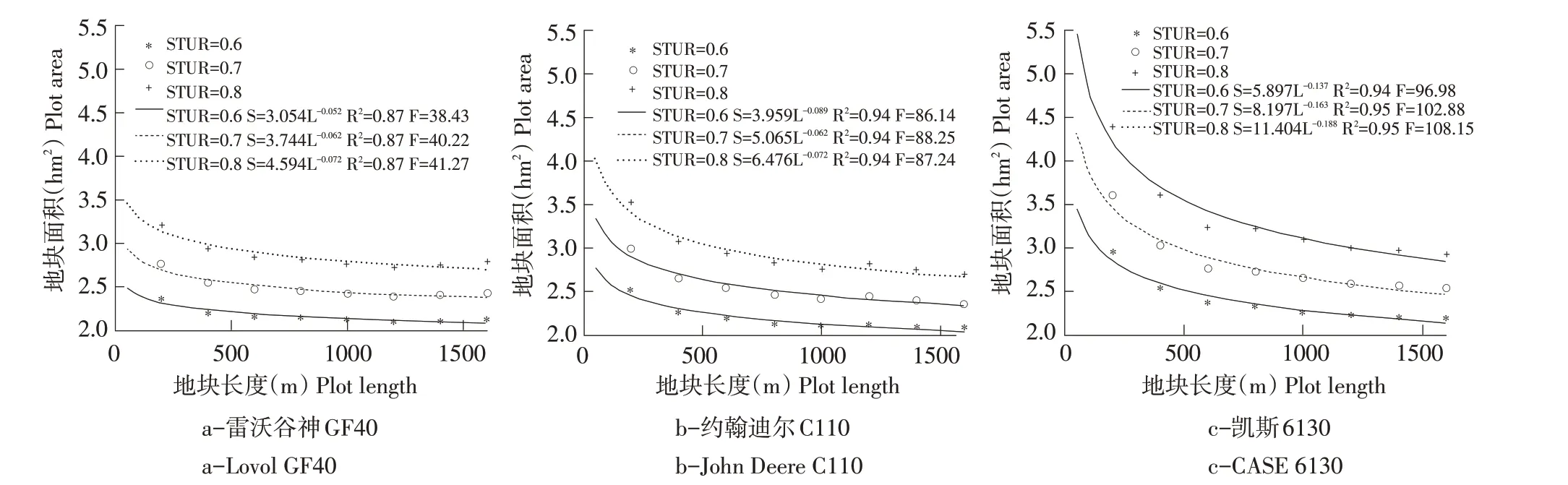
图2 特定STUR收获机组适宜的作业单元地块长度与面积耦合关系Fig.2 Coupling curves of suitable plot length and area at specific STUR for harvesters
图2中3种收获机组适宜的作业单元地块长度与地块面积耦合关系曲线变化趋势相同,但确定时间利用率条件下,不同机组适宜的作业单元地块长度和面积不同,大功率机组作业单元地块长度和面积均比小功率机组大,与余友泰研究结果一致[2],表明收获机组适宜作业单元地块长度与地块面积耦合的定量关系及规律符合实际情况。由图2还可看出,相同作业单元地块面积和长度条件下,不同机型SUTR也不同。如当STUR为0.8、作业单元地块长度为1 000 m时,额定功率较小的雷沃谷神GF40 机组适宜的作业单元地块面积较小,为2.8 hm2;同样条件下,中型收获机组约翰迪尔C110适宜的作业单元地块面积为2.95 hm2,而额定功率较大的凯斯6130 收获机组适宜的作业单元地块面积为3.2 hm2。
3.2 收获机组适宜作业单元地块条件耦合规律应用
由图2 可知,每条特定STUR 曲线可将坐标系第一象限分为两部分,该曲线及其上方点代表可使该收获机组STUR达到和超过特定时间利用率的作业单元地块条件,曲线下方点代表收获机组STUR低于特定值时对应的作业单元地块条件。
若设:在坐标系第一象限中,点A(La, Sa)是STUR 为τn时,收获机组H 适宜的作业单元地块长度和面积耦合曲线上的点,而点B(Lb, Sb)和点C(Lc,Sc)为收获机组目标STUR 为τs时作业单元地块长度与地块面积耦合曲线上的两点,且Sa≥Sa、La≥Lc,如图3所示。则有如下判断:
①当La≥Lb或Sa≥Sc时,说明点A 在目标SUTR对应作业单元地块条件耦合曲线τs的右侧或上方,此时若选用收获机组H,有τn≥τs,说明收获机组H适宜在点A 对应的地块上作业,且可以获得较高STUR;
②当La 依据上述结果及判断可在已知作业单元地块条件下选择适宜作业的收获机组型号,或在已知机组型号条件下选择其适宜作业单元地块条件。 图3 机组适宜作业单元地块条件耦合关系应用Fig.3 Application of the coupling relationship between suitable plot length and area for combine harvesters a.界定农业机组作业季节时间利用率(STUR)概念,建立STUR计算模型可清晰直观表达时间利用率与作业单元地块条件间定量关系,为分析时间利用率随作业单元地块面积与地块长度变化规律奠定理论基础。 b.确定STUR条件下,收获机组适宜作业单元地块面积与地块长度呈幂函数关系耦合变化,收获机组适宜作业单元地块长度和地块面积均随机组功率增加而增加,明确作业单元地块长度和面积与收获机组功率的定量匹配关系。 c.收获机组目标STUR曲线可将坐标系第一象限分为两部分,曲线及其上方的点代表收获机组STUR 可达到和超过目标STUR 的作业单元地块条件,是收获机组适宜作业区;曲线下方点代表收获机组SUTR 低于目标STUR 时对应的作业单元地块条件,是收获机组非适宜作业区。当STUR 为0.8、作业单元地块长度为1 000 m 时,雷沃谷神GF40、约翰迪尔C110和凯斯6130三种收获机组适宜地块面积分别为2.8、2.95和3.2 hm2。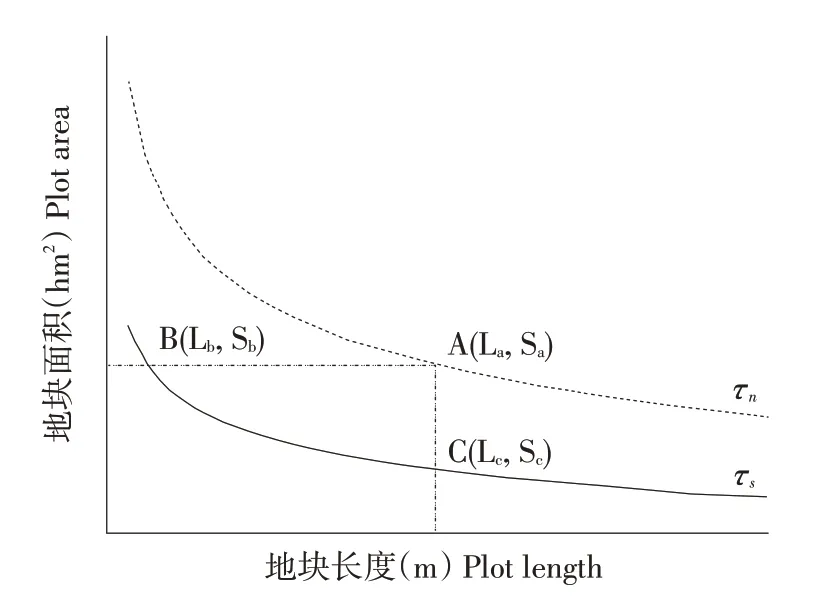
4 结 论

