基于GA-DE算法的开孔外壳屏蔽效能预测与优化

赵旭东,王一凡,赵 阳,张哲民,陈泽南,刘守城

(1.南京师范大学南瑞电气与自动化学院,江苏 南京 210023) (2.江苏省电气装备与电磁兼容工程实验室,江苏 南京 210023) (3.江苏益邦电力科技有限公司,江苏 南京 210001) (4.南京四方亿能电力自动化有限公司,江苏 南京 210001)

近年来,随着电力电子设备的快速发展,电子设备工作频率的不断提高,电磁干扰噪声问题也日益严重[1],导致周围电磁环境越来越差,严重影响了周围电力电子设备和自身设备的稳定运行. 实际工程中因散热和接线,箱体外壳往往会带有孔缝,产生电磁泄露,大大降低了外壳的电磁防护能力[2-3]. 电磁屏蔽作为抑制辐射电磁干扰噪声最简单直接有效的方法[4],吸引了众多国内外学者的研究和关注.

屏蔽效能可以通过实验或计算得到,实验会消耗大量资源且可重复性差. 所以要寻求合适的计算算法,快速准确地预测屏蔽腔体的屏蔽效能对屏蔽腔体的设计具有重要的意义. 目前屏蔽腔体屏蔽效能的计算方法主要包括数值计算法和解析计算法两种. 数值计算法包括时域有限差分法(FDTD)、有限元法(FEM)、矩量法(MOM)与传输线模型(transmission line modeling,TLM)等. 通过数值计算方法可以在宽频带下预测复杂腔体的屏蔽效能,其缺点是计算量较大. 解析计算法比数值计算法有更多的限制(如无法对复杂的物理结构进行分析、存在较多近似等),但在结构简单的情况下也可以得到较为精确的结果,与数值计算法相比,其计算速度更快,占用内存更少. 目前对外壳屏蔽效能的计算均存在计算量大和计算结果不准确的问题. 本文采用GA-DE算法获得准确的等效电路模型参数[5],预测开孔外壳屏蔽效能,使得计算量更小,计算结果更加精确.

1 开孔外壳电磁屏蔽特性仿真与分析

通常用屏蔽效能(shielding effectiveness,SE)来衡量外壳的屏蔽效果,电场和磁场屏蔽效能定义分别为[6-7]:

SEE=20lg(E0/Es),

(1)

SEH=20lg(H0/Hs).

(2)

式中,H0和E0表示未加外壳时某点的电场和磁场大小,Hs和Es表示加外壳后该点的电场和磁场大小,屏蔽效能的单位为dB. 在本文中以电场屏蔽效能为度量结果,其数值越大代表屏蔽效果越好,数值越小代表屏蔽效果越差[8-9].

本文研究外壳开孔对电磁屏蔽效能的影响. 根据外壳物理结构,利用Solidworks软件构造外壳物理模型,并将物理模型导入电磁仿真软件CST中进行电磁仿真分析,外壳模型示意图如图1所示. 外壳参数为:a=50 cm,b=120 cm,c=60 cm,e=15 cm,f=10 cm,g=5 cm,h=8 cm. 外壳厚度t为3 mm.

探究外壳开孔后屏蔽效果的变化,本文使用CST中的EMC/EMI(Radiated Emission)模块对开孔外壳屏蔽情况进行仿真[10],将画好的开孔外壳模型图导入到CST中,设置外壳参数,外壳材料为铝,磁导率是11 H·m-1,电导率是35 400 000 S·m-1. 因为本文需要代入传输线模型模式,将仿真的激励源设置为电场矢量垂直传播方向,圆形极化,电场模为1 V·m-1的平面波,探针分别设置为壳体几何中心P点及壳体中轴线线上距离壳体正面25 cm的Q点.壳体几何中心P点的屏蔽效能仿真结果如图2所示.

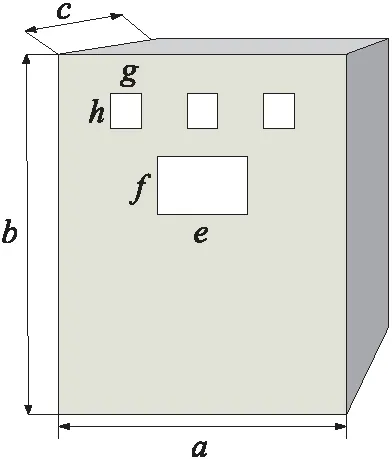
图1 开孔外壳模型图Fig.1 Open-hole shell model diagram

图2 P点屏蔽效能仿真结果Fig.2 P-point shielding effectiveness simulation results

由图2可知,在100～780 MHz上,壳体几何中心P点的屏蔽效能随着频率的提高而降低,在780～1 000 MHz上,屏蔽效能随着频率的提高而提高. 780 MHz 时的屏蔽效能为仿真图像的最低点,分析为谐振频率点,由于入射波与反射波叠加产生.

2 基于GA-DE算法的开孔外壳屏蔽效能研究

2.1 开孔外壳的传输线等效电路

开孔可以等效为一段终端短路的无损耗传输线,屏蔽外壳可以等效为终端短路的波导[11-12],传输线电报方程为

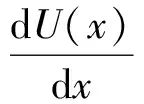
(3)

(4)

式中,U(x)和I(x)分别为传输线上任意点的电压与电流,h为传输线间距,L为传输线电感,C为传输线电容.图3为屏蔽外壳等效电路.根据传输线理论、戴维南定理及屏蔽效能定义式[13],观测点P处的等效电压源V1、等效阻抗Z1、负载Z2和等效电压Vp及屏蔽效能SEP,

(5)

式中,kg、Zg为矩形波导的相位阻抗和特征阻抗,yp、d分别为观测点位置坐标与屏蔽外壳几何尺寸,k1、k2、k3分别为算法优化得到的开孔阻抗参数、开孔形状参数及位置参数,SEp为观测点位置屏蔽效能的预测值,Zap为P处等效电阻,Vap为电阻上电压.

图3 屏蔽外壳等效电路Fig.3 Equivalent transmission line circuit

2.2 基于GA-DE算法的参数提取

根据的壳体中央位置的屏蔽效能信息,本文通过GA-DE算法来获取式(5)中的参数k1,k2,k3,先利用GA处理开孔外壳屏蔽效能信息来获取等效参数的初始值,然后利用DE算法进行优化得到最终的等效参数[13]. 具体过程如下.

Step 1:编码

实数编码,构造线性变换

fj=aj+xj(bj-aj).

(6)

将定义域[aj,bj]的第j个变量fj映射到区间[0,1]上的实数xj,j=1,2…N.

Step 2:初始化种群

产生w个,z组,其中每组d个[0,1]区间内的均匀随机数,可以得到{uj},将每个uj当做初始群体的父代个体值xj,w表示子种群数,z表示每个子种群数内的个体数,优化参数个数用d表示,系统模型平方和用Q表示,Q最小构造优化准则函数.

(7)

式中,φ(f)表示实测阻抗值,φ(fi)表示理论计算值.

经式(6)优化变量值后,再通过式(7)得到目标函数值.

Step 3:适应度评价

目标函数值Q(xi)代表个体适应能力.Q(xi)越大表示适应能力越弱,Q(xi)越小表示适应能力越强.适应度评价函数为

(8)

式中,τ=0.001.

Step 4:选择操作

每一个子种群在父代的个体中按比例选择方式以概率pi选第i个个体,共选n组个体,按轮盘赌被选概率为

(9)

Step 5:交叉操作

每一个子种群中任意两个个体算数交叉,随机线性重组之后新个体为

(10)

式中,u1,u2为[0,1]内均匀分布随机数.

Step 6:变异操作

在每个子种群父代染色体上基因添加小概率pm=1-pi的扰动,维持多样性,防止早熟.

(11)

式中,u(j)和均为随机数,j=1,2…n.

Step 7:判别收敛

当个体目标函数值小于设置值时或者算法达到设置的进化次数时,结束运行.种群中最优个体为所求方程参数,最优估计值的结果是等效参数的初始值,记为k10、k20、k30,分别代表等效开孔阻抗参数、开孔形状参数和位置参数的初始值.否则,转入Step 4,重新评价、选择、交叉和变异操作.

进一步地,利用DE算法优化上述过程得到的结果,Z是屏蔽效能表达式,样本测量屏蔽效能Zx为100～1 000 MHz中900个线性分布不同频的数据. 即探索最小化拟合屏蔽效能和实际屏蔽效能之间的差异. DE参数是按选择原则经过多次比较后的最佳值.

(12)

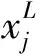
等效参数的优化步骤如下:

Step 1:根据下式初始化种群

(13)

Step 2:变异操作

初始参数值向量是每一代总体,种群内两个个体加权差异作为中间个体,该个体为差异向量;该差异向量加上第3个个体将产生突变,

vi(g+1)=xr1(g)+F·(xr2(g)-xr3(g)).

(14)

式中,F表示诱变因子,F=0.85,xi(g)表示g代种群第i个个体.

Step 3:交叉操作

交换种群个体和对于突变个体的组成部分产生交叉总体,g代种群|xi(g)|交叉运算,变体{vi(g+1)}为:

(15)

式中,jrand表示(1,2,3….D)内随机整数,CR表示交叉概率,CR=0.7.

Step 4:选择操作

当个体目标函数大于候选者目标函数,就用下一代种群代替现在的个体,

(16)

Step 5:收敛判别

算法达到设置次数时或选择的优秀个体小于设置值时,结束算法,估计结果为k10,k20,k30的最佳值. 如未收敛,则返回Step 2继续执行操作. 屏蔽外壳的等效电路参数如表1所示.

图4 Q点屏蔽效能仿真结果和算法结果对比Fig.4 Comparison of Q-point shielding effectiveness simulation results and algorithm results

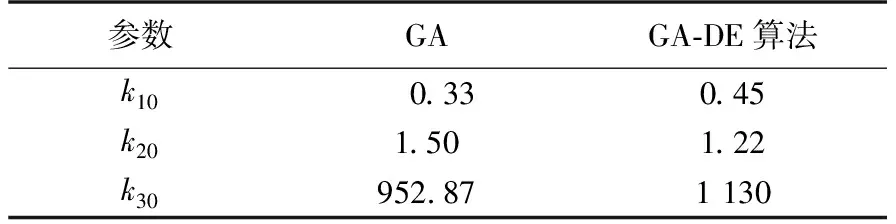
表1 屏蔽外壳的等效电路参数Table 1 Equivalent circuit parameters of shielded enclosure

根据算法参数结果代入公式(5)计算Q点屏蔽效能与仿真结果对比如图4所示.

由图4可知,算法提取参数后的Q点屏蔽效能结果与仿真结果有着较好的重合性和趋势一致性,验证了算法计算屏蔽效能方法的准确性和可靠性,算法结果与仿真结果存在微小差异是由于实验测试中存在误差造成. 在CPU为Inter Core I7的计算机上CST仿真用时约60 000 s,而本文方法用时仅400 s,效率有了很大的提高. 同时,本文算法对不规则外壳开孔的屏蔽效能也能有效预测,也更容易分析各参数对外壳屏蔽效能的影响.

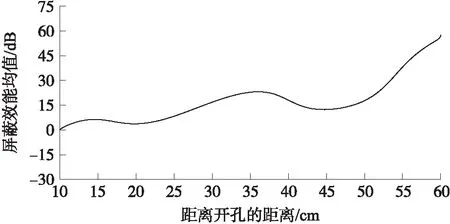
图5 距离开孔面距离对屏蔽效能的影响Fig.5 The influence of the distance from the opening surface on the shielding effectiveness

3 机箱外壳电磁屏蔽优化分析

利用GA-DE算法获取的等效参数,将壳体中轴线上各点屏蔽效能关于频率的平均值作为参考值,根据公式(5)可以得到屏蔽效能与中轴线上点距离壳体正面距离的关系如图5所示.

由此可知,距离开孔面的距离越远,屏蔽效能数值越大,外壳电磁屏蔽效果越好;距离开孔面的距离越近,屏蔽效能数值越小,外壳电磁屏蔽效果越差. 实际应用中外壳屏蔽时应将辐射干扰源远离开孔面摆放,提高外壳的电磁屏蔽性能.

4 结论

本文通过GA-DE算法处理仿真获取的外壳几何中心处的屏蔽效能信息,得到外壳等效传输线电路模型的相关参数,然后对开孔外壳中轴线上其他点的屏蔽效能进行研究,对比了算法结果与仿真结果,重合性较好,在100～1 000 MHz内走势基本一致,证明了算法提取参数后计算得到屏蔽效能结果的正确性和准确性,并通过算法提取的参数计算了距离壳体开孔面不同距离的屏蔽效能情况,为屏蔽体内辐射源的摆放位置提供了依据.