基于几何光学的赋形全向波束单反射面天线设计

钱嵩松,朱浩伟,朱佳乐

(南京理工大学 电子工程与光电技术学院,江苏 南京 210094)

全向天线在军、民领域都有广泛的应用需求。例如基站通信中,基站天线需要在方位面上具有全向性覆盖能力,而仰角面具有余割平方功率分布的波束,其波束偏轴角可达90°;而在制导寻的中,又需要偏轴角较小的全向型笔状波束。振子天线[1]、环状天线[2]、蝶形馈源组合频选表面[3]等结构可产生全向波束,但通常偏轴角的设计指向范围受限,且增益较低。而反射面天线,不论是单反还是双反结构,通过母线绕轴旋转得到旋转对称反射面,均可实现偏轴角在较大范围可控的全向性高增益赋形波束。例如,国内外均有学者给出了母线为常规圆锥曲线并倾轴放置的双反面射天线[4,5],可实现确定偏轴角的波束指向;通过对主面赋形,可提高笔状波束增益[6]或实现波束的功率分布赋形[7]。文献[8]给出了另一种双反射面天线设计,其赋形主面的母线由多段短圆锥曲线相互衔接而成。与双反结构相比,单反射面横向口径面较大,但纵向剖面短,设计也更简单,且无副面遮挡,因此不存在小偏轴角限制。文献[9,10]给出了具有余割平方功率分布的赋形单反射面天线,结合几何和物理光学设计,通过优化方向图目标函数最终获得所需的反射面母线方程。文献[11]给出的单反射面,其母线也是通过多段圆锥曲线相互衔接而成的,设计过程也同样较为繁琐。文献[12]使用另一种单反实现全向波束的方案,即1个全向性馈源照射1个在其周围旋转的反射面,虽可实现较高的增益,但它需要机扫机构,因而波束也不再是全时全向。文献[13]也给出了一种基于几何光学的偏馈赋形双反射面天线设计,但它着重于近场能量的聚焦与传输,而非实现远场的全向波束。

本文给出了一种基于几何光学且可实现全向波束的单反射面设计,其母线仅由唯一微分方程给定,物理概念清晰明确,设计简单易行;由能量守恒给出的波形映射关系,可实现任意功率分布的波束赋形,且波束偏轴角指向设计中没有限制,具有很好的工程适用性。

1 赋形反射面设计

1.1 波束赋形原理

考虑图1所示的情形,1条待定曲线,也即赋形反射面的母线,它将位于焦点PF处馈源发出的能量反射到指定方向,以满足指定的功率分布,焦点至原点间距离记为f。

图1 波束赋形原理示意图

设馈源方向图为Gf(θf),其能量分布角度范围近似为[0,θfmax];经反射后所得的赋形方向图为Gr(θr),其能量分布角度范围近似为[θrmin,θrmax];θr与θf均由天线对称轴,也即图1中x轴负向计起。根据能量守恒原理有

(1)

右侧Gr(θr)的积分限也可能是从θr至θrmax,这要根据具体设计中馈源射线小偏角是对应反射射线的小偏角还是大偏角确定。式(1)中系数K为

(2)

在给定Gf(θf)与Gr(θr)的条件下,由能量对应关系可知θr必是θf的单调函数,但该函数关系并不易直接求出。为此,通过数值积分技术,分别得到2个方向图积分函数P(θf)与P(θr)的数值解,然后由曲线拟合分别得到P(θf)与θr(P)的近似解析函数,由此获得2个方向图间的角度映射函数θr(θf)。

1.2 反射面赋形

波束赋形需通过反射面赋形实现。如图2所示,记入射线与x轴负向夹角为α,反射线与x轴正向夹角为β,对应于上述馈源照射赋形反射面的情况,即有α=θf,β=π-θr,因此α和β间也有确定的单调映射关系,记为β=g(α),该函数将在后述微分方程中使用。

根据几何光学斯涅尔定理可知,待定曲线在反射点A处切线与(α+β)角平分线垂直。分析图2所示β>α、β=α或β<α3种可能,(α+β)角平分线与x轴间的夹角均可写为(β-α)/2,因此待定曲线在反射点处斜率即可写为

(3)

式中

(4)

角β由函数g(α)与变量x及y联系起来。因此式(3)即唯一确定了赋形曲线所应满足的微分方程。通过龙格-库塔法求解该方程,即可得到所需赋形反射面母线的数值解。相比于文献[10]中所述的多段圆锥曲线拼接方法,该方法的物理概念非常清晰。

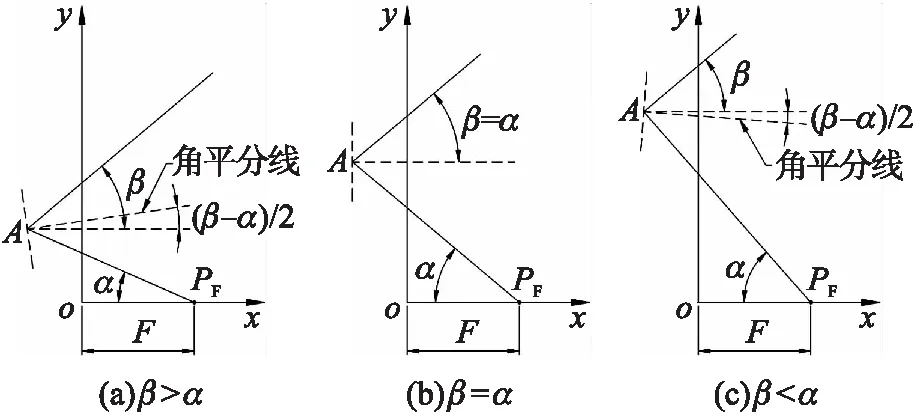
图2 赋形曲线在反射点处切线图

微分方程的求解,还需确定初值(x0,y0)。对于图2所示坐标系,设定赋形曲线从原点开始,因此理论初值为(0,0)。但以(0,0)为龙格-库塔法求解的初值,会导致数值解永在(0,0)。工程上的解决方法是根据曲线实际的初始倾斜方向,将初值y0设为0,而将x0设为1个非常小的负值或正值即可。

2 算例仿真

为验证上述设计方法的有效性,给出2种赋形波束设计算例,一种是余割平方功率分布波束,另一种是笔状波束,中心工作频率均设为f0=35 GHz。

2.1 馈源

为实现全向波束,馈源采用横电磁波模式(Transverse electromagnetic mode,TEM)同轴喇叭,其结构如图3(a)所示。它的波束是全向性的,但偏轴角较小,增益较低,波束较宽。设其口面内外半径分别记为ri与re,则其方向图函数可近似为[11]

(5)

式中:J0(·)是第一类0阶贝塞尔函数。同轴喇叭的主波束张角应与反射面相配合,以确保其主要能量均能被拦截反射,60°是1个工程上较合适的选择,ri=0.45λ0及re=0.9λ0可满足该要求。图3(b)给出了1个f0=35 GHz的TEM同轴喇叭数字仿真软件(Computer simulation technology,CST)仿真方向图以及解析式(5)计算曲线,两者吻合较好,主要能量可认为限定在60°内,因此积分计算中可取θfmax=60°。图3(c)给出了圆锥喇叭的S11参数仿真结果,在30～40 GHz范围均有较低的回波损耗。

图3 TEM同轴喇叭及其仿真结果图

2.2 余割平方波束

所谓余割平方波束,即天线功率方向图Gr(θr)可近似为[8,10]

Gr(θr)=G0rcsc2(θr-π/2)

(6)

式中:设θr的角度范围为θrmin=95°,θrmax=135°。根据前述方法,可得β与α的映射函数g(α)如图4(a)所示,所得赋形曲线如图4(b)所示,其焦距f=4.5λ0,口面半径R=19λ0。以前述同轴喇叭馈源照射,所得仿真波束如图4(c)所示,同时图4中也给出了余割平方函数计算结果,两者趋势一致。

图4 余割平方反射面及其仿真结果图

2.3 笔状波束

对于笔状波束,β角不是α的函数,而是1个固定值。根据实际工程需求,取β=40°,由此得到的赋形曲线如图5(a)所示,其焦距f=5.4λ0,口面半径R=10λ0。它的仿真波束如图5(b)所示。与余割平方波束相比,它不存在散焦问题,因此具有更高的增益。

3 测试与讨论

因工程所需,对β=40°笔状波束反射面天线进行了加工测试。微波暗室测试环境如图6所示。馈源的测试方向图、S11及赋形反射面天线整体测试结果如图7所示。

图5 笔状波束赋形反射面及其仿真结果图

图6 笔状波束赋形反射面天线测试现场图

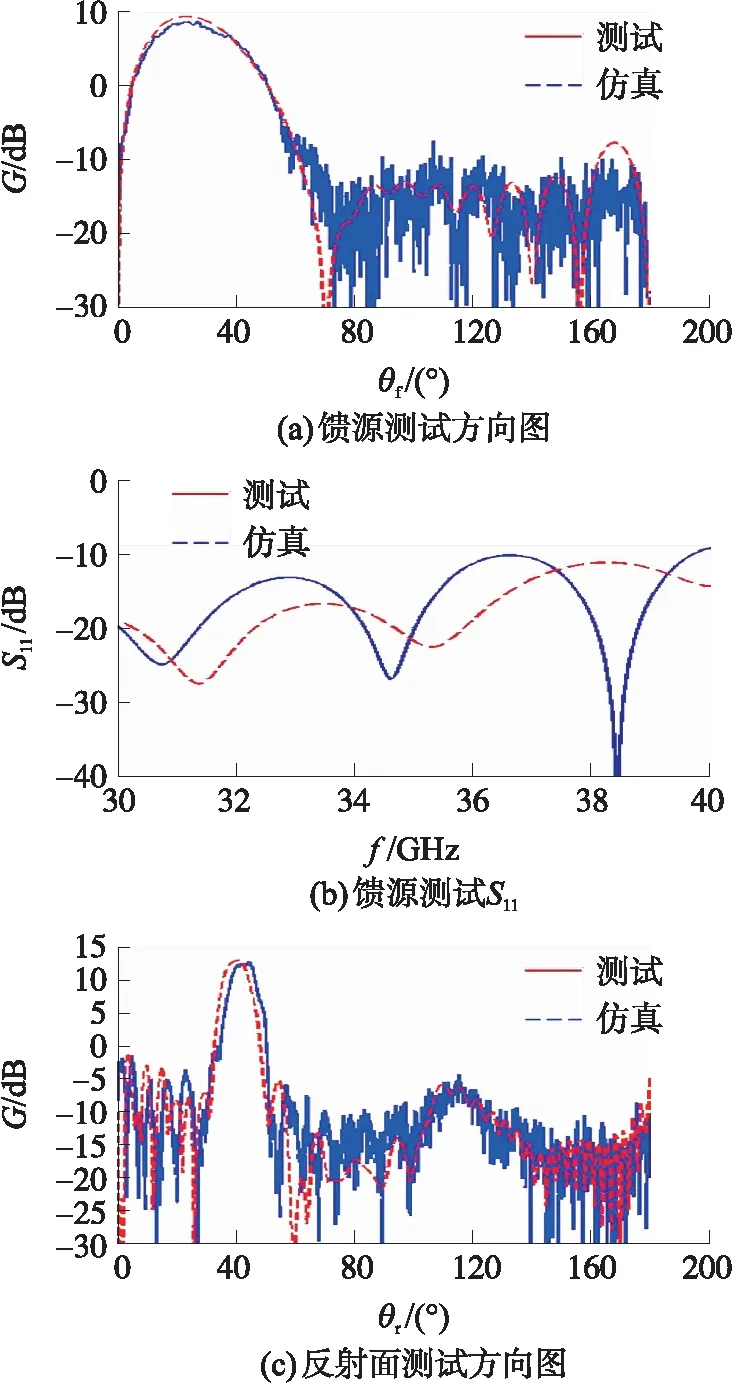
图7 笔状波束赋形反射面及其馈源测试结果图

为便于对比,前述仿真结果也绘于图7中。馈源测试方向图与仿真结果相比,主瓣几乎完全吻合,旁瓣处由于电平较低,测试噪声显得较为明显;馈源的S11测试结果与仿真结果相比总体趋势一致,显示出良好的宽带性能;整个赋形反射面天线的测试方向图也与仿真方向图吻合得很好,增益为12.2 dB,3 dB波束宽度约为8°,仅偏轴角约有2.5°的偏差。

本文设计的天线与文献[4-11]中提到的7种双、单反射面的典型尺寸、性能对比由表1给出。可以看出在实现近似电性能的情况下,本文方法具有一定的结构和尺寸优越性。

表1 本文方法与已有7种反射面天线的性能对比表

4 结束语

本文提出了一种工程上简单易行的赋形全向波束单反射面天线设计方法,可实现波束的任意偏轴角指向及任意功率分布。为表明该方法的适用性,设计了2种单反射面天线,一种具有大偏轴角余割平方方向图,另一种具有小偏轴角笔状波束。事实上,常规单反射面天线也可视为本文所述方法的1个特例,只需令β=0°即可得出所需的抛物线方程。最后,完成了1个40°偏轴角全向波束赋形单反射面天线的加工与测试,所得结果与设计仿真吻合良好,也表明了所述方法的有效性。