基于深度强化学习的高频交易优化算法
饶 瑞,潘志松,黎 维,刘松仪,张 磊,李云波
(陆军工程大学 1.指挥控制工程学院;2.通信工程学院,江苏 南京 210007)
算法交易(Algorithmic trading,AT)[1]是金融领域的研究热点,是指在无人工干预条件下,由计算机按照事先设定好的交易策略执行指令,其核心为交易的算法模型[2]。高频交易(High frequency trading,HFT)[3]是通过频繁交易来赚取买卖差价的一种算法交易[4],可看成在线决策问题[5],包含2个部分:环境特征感知和在线正确决策。这2部分是高频交易面临的2大难点,同时,频繁交易带来的高额交易费用大大影响投资收益。
对金融环境的特征感知,主要是从非平稳的、嘈杂的金融时序数据中提取有效的特征表示。现有的人工提取方法严重依赖于以往经验,易受人为主观因素的影响。针对在线正确决策问题,算法模型不仅要能利用已有的经验,还要能自主探索未知环境,实现动态交互,并在恰当时机做出正确的交易动作。深度学习(Deep learning,DL)[6]具有很强的特征提取能力。强化学习(Reinforcement learning,RL)[7]可进行在线自学习和连续决策,包含智能体(Agent)和环境(Environment)2个部分[8],是一种凭借试错和与环境交互的方式[9]不断进行策略改善,使得累积收益最大的机器学习算法。两者结合后可得到既有感知能力又有决策能力的深度强化学习(Deep reinforcement learning,DRL)[10]算法,可大致将其分为2类:基于值(Valued-based)[11]的强化学习方法和基于策略(Policy-based)[12]的强化学习方法。有学者将两者联合,形成演员-评论家(Actor-critic,AC)[13]算法。基于值的RL先输出值函数,再选择动作;基于策略的RL直接输出动作,但算法不易收敛。AC算法将两者结合,同时含有输出动作的Actor网络和输出值函数的Critic网络,用后者指导前者的动作输出,算法稳定,且收敛较快。DRL在游戏、无人机等领域的成功应用,激起了学者们将其用在量化交易上的浓厚兴趣,且已有不少的研究成果。
文献[14]在3支不同趋势的日级股票上,搭建基于全连接的深度确定性策略梯度(Deep deterministic policy gradient,DDPG)[15]模型,结果表明该模型仅在走势平缓的股票上表现良好,模型泛化能力较差。文献[16]针对高频的小时级数据,在单一证券上进行固定数量交易,对动作进行重塑,搭建基于近端策略优化(Proximal policy optimization,PPO)[17]算法的交易模型,结果表明基于AC的强化学习算法可用于高频交易,且表现较好。文献[18]将异步优势动作评价(Asynchronous advantage actor-critic,A3C)算法[19]运用到分钟级的投资交易上,主要研究不同网络设置(如节点数、随机丢包等)对收益的不同影响。文献[20]将DDPG算法运用在日级股票数据上,进行投资组合,验证了DDPG算法策略的组合收益高于最小方差投资组合策略和道琼斯工业平均指数。文献[14,16,18,20]主要是利用强化学习的自主决策能力解决自动化交易问题,验证AC算法在量化交易上的可行性,没有过多涉及环境的特征提取。
文献[21]使用Q-Learning算法,并在虚拟股票数据上进行实验验证,虚拟数据缺乏可信度。文献[22]首次在量化交易领域应用了基于策略的强化学习方法,并称之为直接强化学习(Direct reinforcement learning,Direct RL),在日级数据上验证了该方法收益效果优于Q-learning算法,但该算法中的递归结构降低了网络的训练速度。文献[23]在日级数据上,先用格拉布斯方法去噪,再搭建基于全连接的Direct RL交易模型,结果表明数据去噪有利于环境信息表征,对策略性能的提升有较大帮助。文献[24]提出基于任务感知的深度Direct RL算法,利用模糊函数对数据进行降噪,并用全连接网络进行特征提取。文献[25]利用门控循环单元(Gate recurrent unit,GRU)网络提取环境特征,进行直接强化学习。文献[5,23,24]重点在数据处理和环境的特征提取方面,验证了环境特征表示对交易策略的性能有极重要的影响,而对于在线决策的算法,则都采用直接强化学习。
现有文献研究有侧重于环境特征提取的,有强调强化学习算法的,日级数据频率偏多,但将两者联合并用于高频交易的较少。在高频交易中,交易太过频繁带来的高额交易费用给算法带来了新的挑战。本文提出融合长短期记忆(Long short term memory,LSTM)网络[25]细胞结构的DDPG高频交易算法模型。在进行连续交易时,利用LSTM可长时间记忆历史数据的特点[26],先将当前时刻的状态传递给其细胞结构,自适应地提取环境特征,该特征是当前状态和历史信息的抽象表示,是环境的综合特征,用于指导后续的交易决策;再利用DDPG算法进行自主学习和连续决策。此外在特定场景下对状态、动作和奖励进行约束重塑,最后在分钟级的上证50指数基金上进行实验验证,并逐一分析细胞结构和重塑奖励对收益的影响。
1 融合LSTM的DDPG高频交易算法
为从高频金融时序数据中获取环境特征,并进行动态连续决策,以获得最大累积收益,本文搭建了1个融合LSTM细胞结构的DDPG深度强化学习高频交易算法模型。
1.1 交易智能体的描述
1.1.1 交易智能体的任务描述
将强化学习应用到量化交易上,其学习目的是为了得到1个从状态到动作的最优映射策略π*,使得交易智能体在未来连续的一段时间内,根据该策略进行连续动作选择,可得到最大的累积收益值。因此,交易智能体的目标函数如下
(1)
式中:t′为未来的交易时刻长度,rt为每个交易时刻的单步收益值。由于智能体的训练集和测试集不同,因此对交易模型的泛化能力要求更高。
1.1.2 状态特征、动作和奖励设置
环境状态一般包括原始金融时序数据特征和人工提取的技术指标,记pt为t时刻的收盘价,相邻时刻的收盘差价为Δpt=pt-pt-1,t时刻的持仓量为pot,则在时刻t,环境的状态特征向量如下
ot=[Δpt-t′+1Δpt-t′+2… Δptpot-1]
(2)
t时刻的状态特征由前t′时刻内相邻时刻的收盘差价和t-1时刻的持仓量组成。Agent在t时刻的动作包含做空、持有和做多,分别用-1、0和1表示。由于高频交易频繁换仓,交易费用在很大程度上决定了收益高低,式(3)是常用的单步奖励函数[20]。
rt=at*Δpt-c*|pot-pot-1|
(3)
记C=c*|pot-pot-1|,表示发生交易时的手续费,式(3)表明,奖励函数即为收益函数,当不进行交易时,无交易费用;否则,加入交易费用。
1.1.3 状态、动作和奖励的重塑
本文仅对单一标的物进行固定数量的操作,每次交易数量为1,且不进行加仓操作,因此状态和动作需满足此约束,对其进行重塑,它们之间的转移关系见图1。

图1 状态-动作转移示意图
图1中,长方形表示交易智能体的重塑状态,圆形表示交易动作,椭圆形是对应动作的奖励值。Agent从无交易观望开始,进行做多建仓(或做空建仓),单向收取交易费用(建仓时不收,平仓时收取),奖励值r=0,持仓量po=1(po=-1);由于不进行加仓操作,因此当相邻2个时刻的动作相同时,Agent则进入做多持有(或做空持有)状态,奖励值r=a*Δp,持仓量po=1(po=-1),保持不变,无交易费用;当相邻时刻的动作不同时,则进行平仓操作,可由建仓状态(做多建仓或做空建仓)或持有状态(做多持有或做空持有)转移到平仓状态(做多平仓或做空平仓),奖励值中需考虑换仓的手续费,为r=a*Δp-C,持仓量po由1(-1)变为0。若不考虑换仓费用,则Agent会不计交易成本,不断进行建仓—平仓—建仓操作,在实际交易中,交易成本必须纳入考虑,在追求低买高卖时,保证扣除交易费用后,收益越大越好。
奖励函数引导交易智能体向着累积收益最大的方向更新。在式(3)中,奖励设置仅考虑了交易费用。但在实际中,交易费用与平仓的交易价格息息相关,价格高低对收益影响很大。因此在奖励函数中加入收盘价pt进行重塑如下
(4)
1.2 融合LSTM细胞结构的DDPG交易算法
1.2.1 LSTM网络的细胞结构
金融时序数据具有很强的相关性,历史数据中含有的某些信息对后续的交易决策有一定的指导作用,自适应地从历史数据中提取有用信息十分重要。LSTM网络常用于处理时序数据,其基本构成单元称为细胞(Cell),具有对过去信息的记忆功能,记忆信息的更新通过细胞中的门(Gate)结构实现,门的实质是加了激活函数的单层神经网络,可实现对信息的筛选如下
Gate=f(x*w+b)
(5)
式中:x为输入向量,w和b为网络学习的权重和偏置,f(·)可为不同形式的激活函数。
细胞结构见图2。图2中ot为智能体的状态特征向量,ht为细胞的输出值,同时也是提取到的环境特征。ct为细胞状态,用于保存历史信息,“×”表示向量各位置对应相乘,实现信息的筛选,“+”表示向量各位置对应相加,实现信息的更新。ft、it和o′t依次为遗忘门、输入门和输出门[27]的值,计算同式(5)。σ为sigmoid函数。经过遗忘门和输入门进行细胞状态更新,见式(6),接着新细胞状态通过输出门得到细胞输出值如下
ct=ft×ct-1+it×tanh(wi·[ot,ht-1]+bi)
(6)
ht=tanh(ct)×ot
(7)
式中:ct中同时含有之前时刻的历史信息ct-1和ht-1以及当前时刻的输入信息ot,ht是对新细胞信息ct的自适应输出,该值是当前输入信息和历史信息的1个综合特征表征,不仅是对环境的特征提取,还能指导后续的动作决策。这说明在进行交易时,综合考虑了当前可获得的显示信息和隐藏在历史数据中的隐性信息。
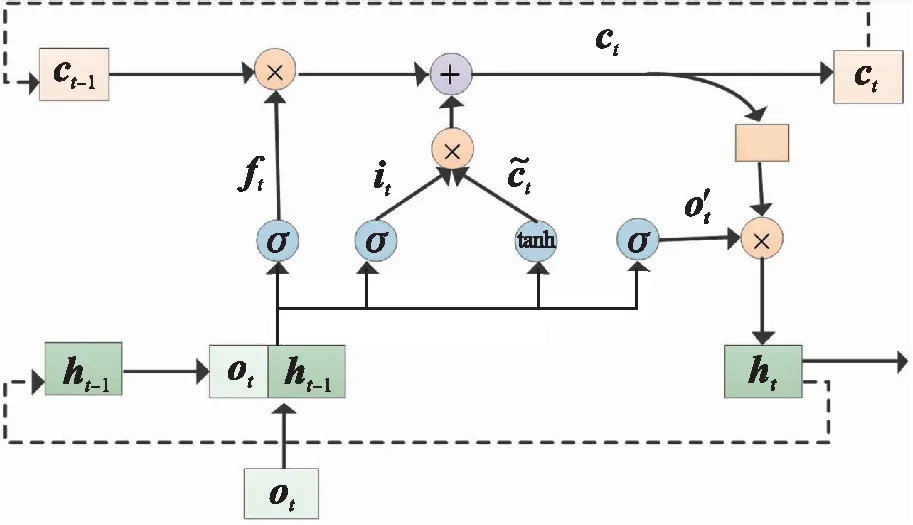
图2 LSTM细胞结构示意图
1.2.2 融合LSTM细胞结构的DDPG算法
DDPG算法是AC算法之一,其前身——确定性策略梯度(Deterministic policy gradient,DPG)算法[12]使用Q表记录值函数,而它使用深度网络来近似值函数,本文用它来最大化投资收益。在LSTM网络中,通常会同时处理多个时间步的数据,但强化学习在交易算法中进行的是单步连续操作,动作间相互影响,前一交易完成后,细胞状态的信息更新和持仓量的变化都将影响后续的交易决策。本文将LSTM单元融入交易智能体后,相邻时刻间的交互流程框架见图3。

图3 相邻交易时刻智能体与环境的交互示意图
图3展示了相邻交易时刻智能体与环境的互动,横轴为交易时间轴。纵向来看,在每一时刻,智能体中的输入信息除环境的状态向量ot外,还包括前一时刻LSTM细胞的隐藏输出ht-1和细胞状态ct-1,智能体的动作作用于环境外,还会影响下一时刻持仓量的变化。LSTM细胞为全局的特征提取器,主要是为了自适应保存和传递位于t′时刻之前的数据信息,以提供给交易智能体更多有价值的信息,帮助其做出更准确的交易动作。图3中的DDPG智能体,除了LSTM细胞外,还包括4个网络,具体结构以及单步交易中的网络更新见图4。

图4 单个时刻中DDPG交易智能体更新示意图
在图4中,除交易环境外,其余为DDPG交易智能体,其中的左侧为DDPG算法中的执行者(Actor)模块,右侧为其评论者(Critic)模块。每个模块中分别含有在线网络(Online net)和目标网络(Target net),这2个网络结构完全一样。强化学习要求状态间尽可能独立,因此先用经验回放(Experience replay)存储经验样本,再用随机方式采集样本更新网络。训练时在线网络实时更新,目标网络采用软更新策略,引入目标网络有助于训练稳定。图4中LSTM细胞为图2所示细胞结构。令Actor模块的在线网络和目标网络的参数为θ和θ-,Critic模块的在线网络和目标网络的参数为φ和φ-。则算法步骤如下:
(1)金融环境给出状态特征ot,首先传递给Agent中的Actor网络,先经过LSTM细胞单元提取环境特征ht,见式(7),再将特征ht送入决策网络,计算动作at=μ(ot;θ);
(2)环境转移状态到ot+1,并给出奖励值rt;
(3)存储经验样本(oi,ai,ri,oi+1)到经验池;
(4)利用随机方式,在经验池中采集N个经验样本,进行网络更新。首先,把采样样本的(oi,ai)送到Critic的在线网络,得到Qi(oi,ai;φ);接着用Actor的目标网络计算动作ai+1=μ′(oi+1;θ-);得到下一时刻的动作后,进一步计算目标Q值,如下
(8)
通过均方误差计算Critic的在线网络的损失,如下
(9)
Actor的在线网络的损失如下
(10)
通过梯度计算,更新在线网络如下
φ←φ+lr*L(critic;φ)
θ←θ+lr*L(actor;θ)
(11)
式中:lr是学习率,最后通过软更新(Soft update)策略,更新对应的目标网络参数如下
φ-←υφ+(1-υ)φ-
θ-←υθ+(1-υ)θ-
(12)
式中:υ是1个很小的值,称为更新系数,文中取0.01。
2 实验结果
2.1 数据说明及参数设置
数据来源:SSE 50股指期货,代码:000016,采样频率:1 min,时间范围:2018-01-02 09:30至2020-07-01 10:00,共145 000条数据,前70%为训练集,后30%为测试集,收盘价走势见图5。
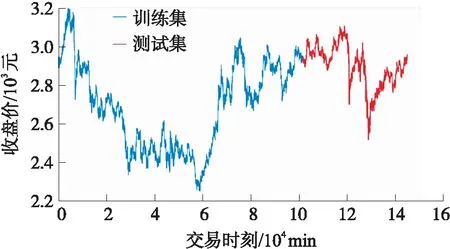
图5 收盘价走势及数据集划分图
图5中,蓝色为训练集,红色为测试集。在训练集上,价格呈现“波动下降—急剧上升—震荡”的模式;在测试集上,呈现“震荡—急剧下降—波动上升—急剧下降—震荡上升”的模式。价格无固定规律。
交易智能体的训练环境为Ubuntu16,使用Pytorch框架,智能体每min进行1次决策,训练时交易费用为收盘价的0.02%。在Actor网络中,LSTM细胞结构输入大小为61,隐层单元大小为128,Decision网络为2层全连接,第1层的输入和输出维度均为128,使用Relu激活函数,第2层的输入和输出维度分别为128和1,使用Tanh激活函数;Critic网络也是2层全连接,第1层的输入和输出维度分别为300和128,使用Relu激活函数,第2层的输入和输出维度分别为128和1。经验池的设置:经验池大小为50 000,随机采样的样本数N为32,学习率为0.000 1,优化器Adam,折扣系数为0.95。
2.2 评价指标及对比策略
利用不同的策略在不同评价指标上进行实验对比,并在不同交易费用下,验证本文算法动作执行的高效性。
2.2.1 评价指标
本文用到的评价指标有累积收益(Cumulative profit)曲线、最终收益(End profit,EP)、夏普比率(Sharp ratio)[28]、完整交易次数(Complete transaction times,CTT)。
累积收益曲线:从测试集开始到结束,在每一个时刻,根据交易策略自动连续执行交易动作,得到的收益累积值。最后1个时刻对应的累积收益值,即为最终收益值,该值可反映策略的盈利情况。
夏普比率:在承受单位风险的情况下,策略的收益情况[29]。值越大策略越优。定义如下
(13)
式中:E(R)和σ(R)分别为收益的期望值和标准差,Rf为无风险利率。
完整交易次数:在整个测试期间,进行完整交易的总次数。该指标对收益影响很大,频繁换仓操作会带来高额的手续费用。
2.2.2 对比策略
本文使用的交易算法为融合LSTM细胞结构的DDPG算法(DDPG-LSTM),对比策略如下:
(1)买入持有(Buy holding),即从交易的第1个时刻开始做多买入,保持做多持有,直到交易的最后1个时刻将其做多平仓。
(2)基于全连接的DQN算法[21](DQN-FC),使用经典的基于值函数的算法——DQN算法,该算法仅有2个网络,其结构和DDPG-FC中的Actor网络完全一样。
(3)基于全连接的DDPG算法[14](DDPG-FC),该算法将DDPG-LSTM中的LSTM细胞换成FC层,并使用Relu激活函数,其余设置不变。
2.3 实验结果及分析
本文将基于策略自身以及本策略与其他策略在各指标上的表现进行分析论证。首先,本文将LSTM细胞结构融入DDPG算法中,其中有2个关键点:利用细胞结构来更新保存环境历史状态和利用收盘价格进行奖励重塑。控制这2个关键变量进行实验,得到图6。

图6 DDPG算法控制关键变量的收益图
图6中的3条曲线都是在DDPG-LSTM下进行的,交易费用为收盘价的0.01%。其中DDPG-LSTM_0仅用了细胞结构对环境信息的存储,DDPG-LSTM_1仅用了重塑的奖励函数,DDPG-LSTM_2两者都用了。可见DDPG-LSTM_0的收益效果最差,说明在奖励函数中加入收盘价格对算法收益至关重要。在表1中可看到,DDPG-LSTM_1的交易次数约为DDPG-LSTM_2的5倍,而其收益值仅是DDPG-LSTM的1.5倍,动作的平均收益远远低于DDPG-LSTM_2。当交易费用由0.01%上升到0.02%时,从图7中可看到,DDPG-LSTM_1的收益值大幅下降,而DDPG-LSTM_2的收益保持稳定,说明DDPG-LSTM_2对交易费用的包容性更强。综上可得,本文设置的奖励函数以及利用LSTM细胞结构保存和传递环境特征,前者不仅能提升收益,还能大幅降低交易次数,后者能进一步减少交易次数,提升算法在收益方面的稳定性,在面对不同的交易费用时,收益变化幅度在投资者的接受范围内。

表1 DDPG算法控制关键变量的指标值表

图7 DDPG算法对交易费用的敏感度实验曲线图
接下来,将DDPG-LSTM_2用DDPG-LSTM来代替,并分析其在测试集上的表现,见图8。图8(b)曲线中值较大的几处位置对应着图5中价格下跌幅度较大的位置,反映了模型能对稍纵即逝的交易机会做出快速正确的反应。图8(c)中越密集的地方说明交易频率越高,在整个阶段,交易并不均匀,根据价格波动变换交易频率:波动平缓时,保守投资,交易频率低;波动较大时,换仓频繁,才能不错过最佳投资时机。图8(d)中前期收益平稳缓慢增长,准确捕获2次大跌的交易机会后,收益值相应地出现2次激增,最后趋于平稳,最终的累积收益为正。最后,将DDPG-LSTM算法与其他策略进行对比,见图9和表2。

图8 DDPG-LSTM策略结果图

图9 各策略的收益曲线图
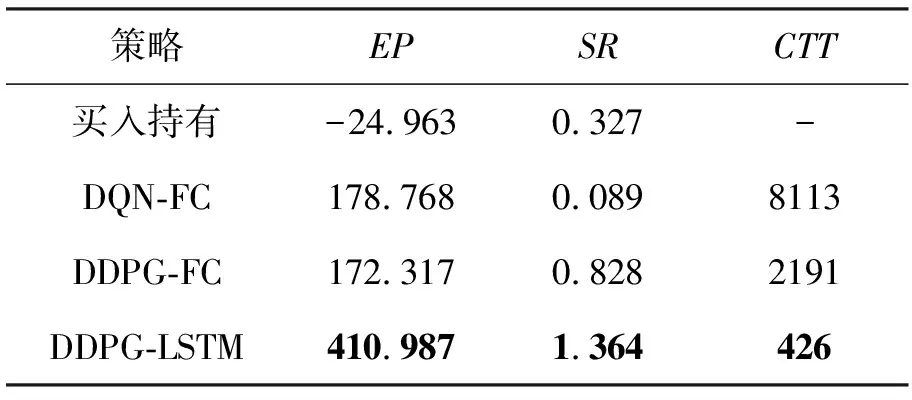
表2 各策略的指标值表
分析图9和表2:首先,除买入持有策略外,其余策略最终都能获利,说明深度强化学习算法在高频交易中的可行性高;其次,策略DDPG-LSTM优于其他策略,最终收益至少是其余策略的2.3倍,夏普比率高达1.364,说明在同样风险下,DDPG-LSTM策略能获得更高的收益,是一种低风险高收益的稳健型投资策略;最后,DDPG-LSTM的交易次数仅为426次,分别约占DQN-FC和DDPG-FC的1/20和1/5,交易少但利润高,说明DDPG-LSTM算法采取行动的有效性高,且较少的交易次数可避免频繁交易带来的高额交易费,对交易费率的包容性更高。
3 结束语
本文搭建了融合LSTM细胞结构的DDPG高频交易算法,并对状态和动作进行重塑,在奖励函数中考虑交易费率和收盘价格,其中收盘价和LSTM细胞结构的联合是算法成功的关键。最后在价格波动大的SSE 50指数基金的分钟级数据集上进行实验,结果表明,该算法策略可实现:
(1)环境特征的有效提取,LSTM细胞结构对当前信息和历史信息进行综合表征,得到1个能有效指导后续交易的环境特征;
(2)捕获稍纵即逝的交易机会,及时做出正确决策,且采取动作的有效性高,避免了频繁交易带来的高额费用;
(3)在奖励函数中加入收盘价并利用LSTM细胞结构对历史信息进行保存,不仅能提升收益和减少交易次数,还能降低高额交易费率造成的收益不稳定问题;
(4)在面对较高的交易费率时,收益的变化幅度较小。
本文算法没有加入技术指标,为进一步提升投资收益,可在后续工作中加入金融技术特征,进行辅助决策。此外,对单个标的物的投资风险较大,可考虑对多个标的物进行高频投资组合,形成对冲,分散风险。

