基于智能反射面的空地无源干扰技术*

彭玲，徐以涛，王海超，谷江春，丁国如

（陆军工程大学，江苏 南京 210007）

0 引言

近年来，智能反射面（IRS,Intelligent Reflective Surface）和无人机（UAV,Unmanned Aerial Vehicles）技术在通信领域的应用引起了广泛关注[1-2]。智能反射面由大量无源器件构成，并且每个单元能够通过微控制器独立地调控相移和幅值，进而重构无线电磁环境[3-4]。与此同时，无人机具有高机动、广覆盖、低成本和按需部署等优势[5-7]，使得无线传播环境的重构能够更高效。

目前，从通信对抗的角度来看，无人机和智能反射面技术的研究主要以提高通信抗干扰性能为主[8-11]。例如，文献[8] 研究了智能反射面在基于无人机的正交频分多址通信系统中的应用，利用智能反射面的反射波束带来显著增益和无人机的高机动性来提高系统的通信速率。文献[9] 考虑了一个无人机和智能发射面结合的通信系统，通过联合优化无人机的主动波束成形、雷达的被动波束成形以及无人机的轨迹来最大化地面用户的接收功率。

此外，将智能反射面技术应用于干扰领域也逐步引起了研究者的兴趣[12-14]。例如，文献[12] 提出了将智能反射面作为无源干扰机攻击合法通信，强调此种方式不需要任何内部能量便可产生干扰信号。然而，智能反射面与干扰领域相结合的研究还处于初步阶段。一方面，由于智能反射面往往放置于固定设施上，导致干扰缺乏一定的灵活性；另一方面，无人机作为干扰发射机时，无人机固有的有限能耗导致干扰的持续性和性能有限。因此，本文提出了一种基于智能反射面的空地无源干扰系统，具体是无人机搭载智能反射面作为一个无源干扰机，实现快速、精准、低耗能地干扰地面通信用户对。与传统干扰系统相比，所提方案中无人机搭载智能反射面作为一个无源干扰机利用通信用户的信号即可降低通信接收方的通信性能，同时无人机为智能反射面的灵活性提供了可能，进一步降低了通信接收方的通信性能。

为达到干扰效果最优化，本文首先提出了一个地面通信用户对的接收功率之和最小化问题，其优化变量包含了无人机位置、智能反射面相移和幅值。为了求解上述问题，首先将原始的优化问题解耦成三个子优化问题，分别是无人机位置优化子问题、智能反射面相移优化子问题和幅值优化子问题，然后引入半定松弛技术和高斯随机化方法对反射面的相移和幅值优化问题进行松弛求解，并引入连续凸近似方法对无人机位置问题进行求解。进一步，设计交替优化算法对上述三个子问题进行迭代求解。最后，仿真结果证明所提算法比其他的算法能够更有效地降低地面通信用户对的接收功率之和。

1 系统模型

基于智能反射面的空地无源干扰系统如图1 所示，此干扰系统被分为两个阶段。具体而言，阶段1 考虑用户1 作为发射机，用户2 作为接收机，智能反射面利用用户1 的发射信号对用户2 进行干扰；阶段2 考虑用户2作为发射机，用户1 作为接收机，智能反射面利用用户2的发射信号对用户1 进行干扰。其中，位于地面的用户1和用户2 配备单根天线，搭载智能反射面的无人机一直处于用户1 和用户2 的上方。同时，智能反射面装备了N个反射单元，并可通过微控制中心对反射单元的幅值和相移进行调控[15-16]。

图1 基于智能反射面的空地无源干扰系统

1.1 阶段1：对用户2进行干扰

阶段1 包含了用户1—IRS、IRS—用户2、用户1—用户2 三个链路，其信道增益分别表示为G1∈ℂN×1、，其中上标H 表示共轭转置运算，ℂ表示a×b的复值矩阵空间；x1～ CN (0,1)表示从用户1的发射信号服从高斯分布，其传输功率为Pa；Θ1为阶段1中智能反射面的幅值和相移参数。因此，用户2 接收到的总的信号可以表示为：

1.2 阶段2：对用户1进行干扰

1.3 用户1和用户2的接收功率之和

结合式(1) 和(3)，用户1 和用户2 的接收信号之和可以表示为：

为了简化运算，令v为总的噪声之和，即v=v1+v2。进一步，结合(2)和(4)，用户1 和用户2 的接收功率之和为：

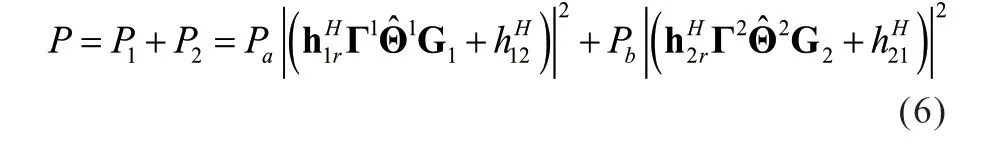
2 优化问题构建及算法设计

2.1 优化问题构建

为了对通信用户1 以及用户2 实时干扰，提出一个用户1 和用户2 的接收功率之和最小化优化问题，如公式(7)所示：

其中，优化变量分别为智能反射面在两个阶段的幅值和相位以及无人机的位置。约束条件分别为智能反射面的幅值约束、相移约束以及无人机与用户间的最大距离约束。

注意到，问题P1 的目标函数包含多个耦合变量，导致问题P1 非凸，难以采用现有的方法直接求解。接下来，为有效地求解问题P1，首先将原始优化问题解耦分解成三个子优化问题，然后提出交替优化方法对三个子问题进行迭代求解。

2.2 给定无人机位置和反射面幅值，优化反射面相移

首先，给定智能反射面的幅值以及无人机的初始位置分别为a1、a2和q=[x,y,z]，则优化问题P1 可以转换为：

注意到优化问题P2 中的约束是离散的，导致原始问题难以直接求解。因此，可将其松弛成连续变量，即。然后问题P2 可以转换为：

注意到优化问题P2.3 中约束rank(M)=1，rank(S)=1导致优化问题仍然是非凸的。为了解决此问题，引入半定松弛（SDR,Semi-definite Relaxation）技术[17-18]。因此，优化问题P2.3 可以转换为：

2.3 给定无人机位置和反射面相移，优化反射面幅值

将求解P2 得到的最优相移解p1，p2和无人机的初始位置q代入到反射面幅值的优化问题中，优化问题P1 可以转换为：

注意到Pa|(a1)Hu1+f1|2是一个凸函数，所以P3.1 是一个凸问题，可以用CVX 求解。相似地，利用高斯随机化方法求得近似的幅值解。

2.4 给定智能反射面相移和幅值，优化无人机位置

将求解P2 得到的最优相移解p1，p2和求解P3 得到的最优幅值a1，a2代入到无人机位置优化问题中，优化问题P1 可以转化为：

注意到优化问题P4.3 的所有约束都是凸约束且目标函数是线性的，因此问题P4.3 是凸的，可以通过CVX 方法有效求解。

2.5 联合优化算法设计

在无人机位置、智能反射面幅值和相移优化的基础上，问题P1 的次优解可以通过交替求解问题P2，P3 和P4 得到。注意到，由于原始问题变量互相耦合，难以得到最优解，因此，给出了一种次优解的解决方案。表1 中算法1 总结了解决问题P1 的全部过程。首先步骤1 对无人机位置，反射面相移、幅值以及判断数值进行初始化；然后步骤2 采用交替下降的方法对无人机位置、反射面相移和幅值进行联合优化，直到无人机位置优化后的功率小于反射面幅值优化的功率结束；步骤3 输出无人机位置、反射面相移以及幅值。

表1 基于智能反射面的幅值和相移以及无人机位置的联合优化算法

3 仿真分析

为了验证所提的联合优化算法的有效性，本节通过MATLAB2016a 平台仿真了基于智能反射面的空地无源干扰技术的接收功率之和曲线，并与基准算法（无任何优化算法）、仅优化相移算法、以及仅优化幅值算法进行比较，具体如下：

首先，对仿真参数进行初始设置，智能反射面的反射单元个数N=100，反射相移随机产生、反射面的幅值都设置为1。用户1 和用户2 的位置分别为u1[0,50,0]和u2[50,50,0]，无人机初始位置q[0,0,10]。针对大尺度衰落考虑的增益L(d)=A(d/d0)-α，其中A 是在参考距离d0的路径损失，被设置为-30 dB。α为路径损耗系数，各个链路的损耗系数表示为阶段1 的用户1 到IRS，IRS 到用户2，用户1 到用户2链路和阶段2 的用户2 到IRS，IRS 到用户1，用户2 到用户1 链路的路径损耗系数α1=α2=2，用户1 到用户2 链路的路径损耗系数α3=3.5。针对小尺度衰落[12]，小尺度信道系数是均值和单位方差为零的圆复高斯随机变量。两个时隙下的噪声功率都为-60 dBm，Pa=45 dBm，Pb=43 dBm。

图2 展示了IRS 反射单元数量N=50 时的接收功率之和的曲线。可以看出，基于智能反射面的空地无源干扰技术的接收功率之和总是低于其他方案的接收功率，这意味着此技术下的干扰性能优于其他方案。在发射功率为1 W的时，基于智能反射面的空地无源干扰系统相较于无任何优化方案有接近11×10-10W 的差距，与仅优化反射面相移的方案有4×10-10W 的差距。

图2 不同发射功率对接收功率的影响图

图3 展示了发射功率Pa=0.3 W，Pb=0.2 W 时的接收功率之和的变化曲线。可以看出，基于智能反射面的空地无源干扰技术仍然具有优越的性能。在IRS 反射单元N=50 时，基于智能反射面的空地无源干扰系统相较于无任何优化方案有接近4×10-10W 的差距，与仅优化反射面相移的方案的差距在1.3×10-10W 左右。

图3 不同反射单元对接收功率的影响图

4 结束语

针对传统干扰方式存在静态有源等不足，本文提出了一种基于智能反射面的空地无源干扰系统，通过无人机搭载智能反射面对地面一对通信用户进行实时干扰。为了优化干扰性能，建立了一个通信用户对的接收功率之和最小化问题，然后设计交替优化算法通过联合优化无人机位置和智能反射面的幅值和相移对原始优化问题进行迭代求解。仿真结果表明，所提算法相较于传统的方法有更好的干扰性能，并且随着智能反射面反射单元数量的增加而增强。在未来工作中，为了进一步提升干扰性能，可考虑将无人机群应用于协同干扰场景中，例如将单无人机的干扰场景推广到多无人机干扰的场景[22]。然而，多无人机协同也存在着一系列的挑战，例如动态环境下的信道高复杂性[23]、干扰的准确性[24-25]、无人机部署[6]等。