6G极化码低时延译码方案*
魏浩,张梦洁,王东明
(1.中兴通讯股份有限公司,广东 深圳 518055;2.移动网络和移动多媒体技术国家重点实验室,广东 深圳 518055;3.东南大学移动通信国家重点实验室,江苏 南京 210096;4.网络通信与安全紫金山实验室,江苏 南京 211111)
0 引言
2008 年,土耳其学者Arikan 基于信道极化的思想提出了极化码[1],并证明了其在二进制输入对称离散无记忆信道下信道容量渐次可达[2],引发学术界与工业界的高度关注。其作为信道编码方案写入第五代移动通信系统(5G)国际标准第一版(3GPP NR Rel-15 版本),并于2018年9 月正式发布[3]。极化码通过信道分裂和信道合并操作引入相关性,从而构造出可靠度不同的极化信道[4]。5G标准给出了不同母码长度的可靠度序列[3],可靠度较高的极化信道承载信息比特进行数据传输,而可靠度较低的极化信道承载冻结比特进行前向纠错,从而实现数据的可靠传输。为了实现任意码长传输,5G 标准设计了速率匹配方案,相应定义了重复、打孔和缩短三种类型比特,可根据码率和可靠度序列进行灵活配置。同时,将循环冗余校验(Cyclic Redundancy Check,CRC)比特与奇偶校验(Parity Check,PC)比特引入标准方案中,作为级联码的外码提升译码性能[5]。
随着5G 商用部署的日臻成熟,业界的研究热点已经开始转向下一代移动通信系统(6G)。相较于5G,6G 时代将面对更高程度的场景多样性和需求差异性,高速率大容量广连接等各项性能指标都将全面提升。其中,超高可靠低时延(Ultra Reliable Low Latency Communication,URLLC)的业务需求受到重点关注,要求中断概率小于10-6且通信时延达到50~100 μs[6,7]。因此,已被严格证明可以没有误码平台的极化码,其有限码长的性能逼近香农容量极限,可以满足超高可靠传输的需求,是6G 最有潜力的信道编码候选方案之一[8]。目前,极化码的主流译码方案是串行消除列表(Successive Cancellation List,SCL)算法[2,9]。当译码列表数较大时,SCL 译码的时间复杂度、计算复杂度和存储复杂度都很高。同时,由于SCL 译码时序的串行特点,也较难实现高吞吐量的译码器[10]。因此,为了应对6G 提出的挑战,业界对高效低时延的极化码译码方案的需求变得愈发迫切。
本文首先介绍极化码原理和5G 标准中极化码的相关概念。其次,定义自由比特和确信比特,提出灵活串行消除列表(Flexible SCL,FSCL)译码算法,实现低时延译码方案。然后,对FSCL 算法译码流程进行阐述。同时,通过仿真实验进行性能验证,并给出译码时延分析。最后总结全文,对极化码的未来应用和研究方向进行展望。
1 低时延译码方案
根据极化现象的信道分裂与合并过程,Arikan 提出采用串行消除(Successive Cancellation,SC)算法进行极化码的译码[2]。通过引入广度优先搜索机制,对于每一个叶节点比特进行多条路径的译码,并分别计算和更新路径度量(Path Metric,PM)值,扩展形成SCL 算法[9]。同时在编码时引入CRC 比特作为级联码,在译码的最后阶段对多条候选路径进行CRC 校验,PM 值最小且通过CRC 校验的译码路径对应的码字作为最终译码结果输出[9,11]。基于CRC 辅助的SCL 算法,相对于Turbo 码、LDPC 码都有显著的性能增益[8],事实上成为了标准推荐和业界公认的极化码主流译码方案。然而,高性能的译码方案也会带来较高的复杂度。设计高效低时延的译码方案,实现高吞吐量的译码器,是应对6G 超高可靠低时延挑战的必然要求。
SCL 算法的译码过程主要包括码树中非译码节点的f/g函数计算和比特递归更新计算,以及译码节点的路径PM 值排序[8,9]。具体实现中,由于计算和存储复杂度可以通过增加硬件资源来解决需求,业界更加关注的是f/g函数的计算量[8,12]。由于SCL 算法基于码树的译码架构和串行译码的特点,码树的每一个非译码节点都需要串行地进行f/g函数的计算,然后再进行比特更新递归信息至其父节点,由此限定了译码过程的时序。因此,尽可能在码树的上层节点进行译码,从而减少f/g函数计算和递归操作的次数,是降低译码器整体译码时延的关键。
1.1 译码节点层级提升
相对于原先在叶节点进行判决译码的SCL 算法,业界提出了固定多比特SCL 算法,每次固定译码2/4/8 个比特[13,14]。与单比特算法相比,在相应的码树中间节点就可以进行译码,译码节点的下层节点不需要计算f/g函数,从而减少译码的时间复杂度。然而每次以固定2/4 比特进行译码,对码树的译码节点层级提升不多(提升1/2个层级),同时固定译码8 比特的算法又会使得路径PM值排序算法的计算复杂度和硬件资源开销极大增加[15]。
根据码树叶节点中信息比特和冻结比特的组合,可以将码树解构为一些特殊类型的节点(或者子树)。如图1(a) 所示,以母码长度为N=16 的极化码为例,码树结构共有5 层,其中d=4 表示根节点,d=0 表示叶节点。根据码树的节点性质,可以将节点分为4 种类型[16,17]。Rate-0 节点为纯白色节点,其所属叶节点全部为冻结比特;Rate-1 节点为纯黑色节点,其所属叶节点全部为信息比特;REP(Repetition)节点为内黑外白色节点,其所属叶节点中,只有最右边一个是信息比特,其他全是冻结比特;SPC(Single-Parity-Check)节点为内白外黑节点,其所属叶节点中,只有最左边一个是冻结比特,其他全是信息比特。整个码树可以看作是由这些特殊类型的节点组成,然后对其译码方案进行低复杂度优化,即是简化串行消除(Simplified Successive-Cancellation,SSC)算法[18,19]。进一步考虑运用列表扩展方案,可以得到SSCL 算法[20,21,22]。
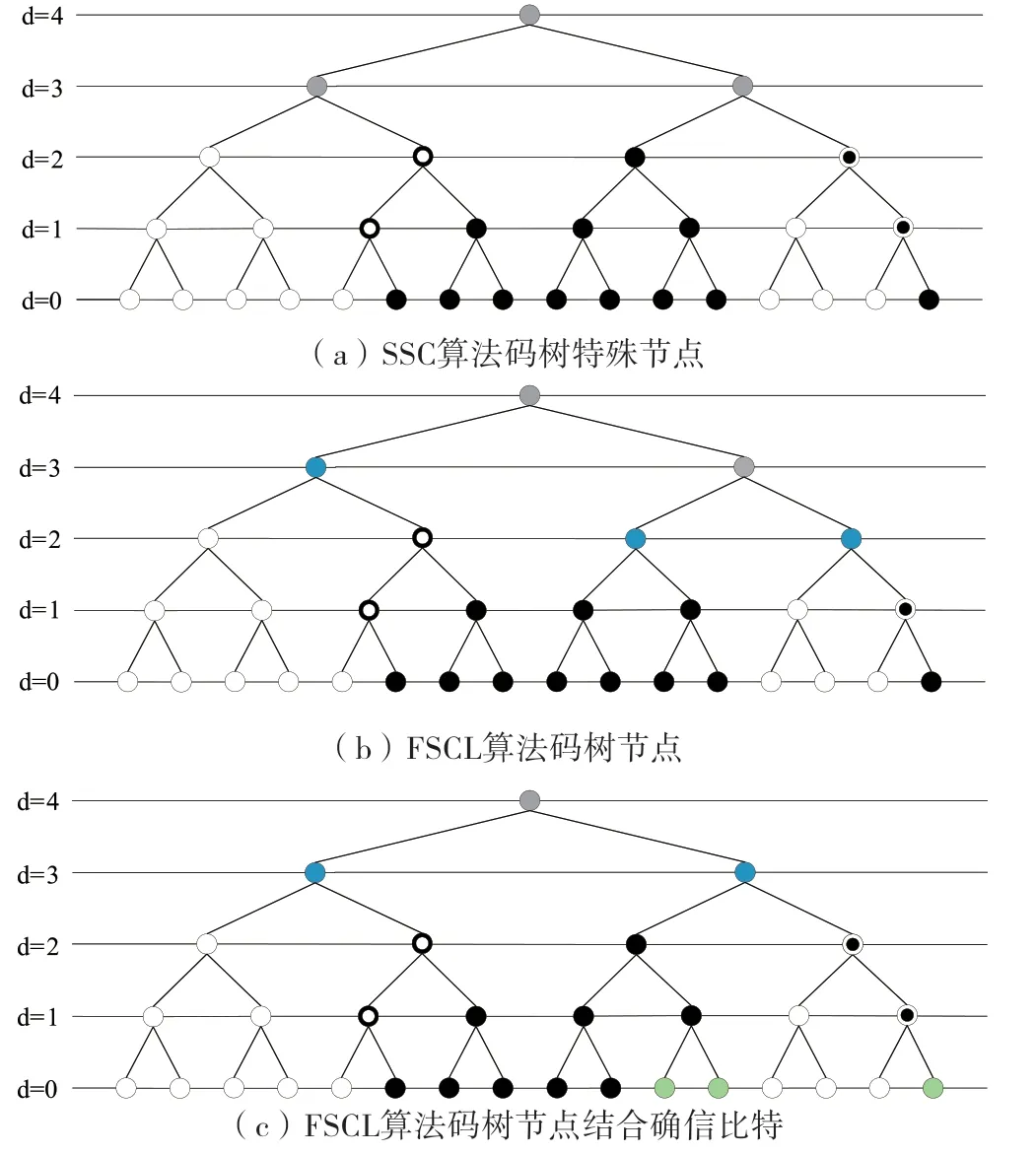
图1 N=16极化码码树节点
SSC/SSCL 算法在码树中对特殊节点进行匹配,尽量实现在上层节点进行译码。其中Rate-0、REP 两种节点的译码算法得到较大简化,但其匹配的子树译码节点通常在靠近叶节点的位置,译码时延降低比较有限。SPC节点的译码算法相对复杂,需要分为多个子类讨论,且只有启发式的方案[20,21]。而Rate-1 节点的译码算法并不能简化,其复杂度与固定多比特算法是相同的。实际中,Rate-R 节点由于其一般性(图1(a) 中的纯灰色节点),才是码树中所占比例最高的,需要重点优化。此外,根据5G 标准,除了信息比特和冻结比特,还有PC 比特等其他类型,可能带来更多的分类和更复杂的节点间关系。
1.2 自由比特路径扩展
综合考虑5G 标准确定的极化码相关的比特类型,可以将信息比特和CRC 比特统称为自由比特(Free Bit,FB),在译码时进行路径扩展;冻结比特、PC 比特、打孔位置比特和缩短位置比特由于协议已经约定其比特值,因此可以统称为协定比特(Agreed Bit,AB),在译码时不进行路径扩展[23]。
由前文所述,固定多比特SCL 算法和SSC/SSCL 算法,都是为了提升码树的译码节点层级。前者关注于译码节点所属叶节点的数量,但受限于计算复杂度,每次译码的比特数较为有限(业界一般推荐每次译码4 比特的方案);后者根据译码节点所属叶节点的特殊组合进行分类匹配,但这些特殊节点在码树中所占比例不高,而且还需要通过译码节点的比特再计算得到叶节点的比特。因此,两种算法虽然一定程度提升了译码效率,但并没有充分利用码树的特性。
通过对码树特征和SCL 算法的分析可知,译码节点的计算复杂度主要取决于路径扩展的规模。由于协定比特不进行路径扩展,因此决定路径扩展规模的,不是译码节点所属叶节点的数量,而是其中自由比特的数量。于是,提出一种灵活的SCL(Flexible SCL,FSCL)算法,基于其所属叶节点中自由比特的数量,来判决是否在当前码树节点进行译码。以图1 中的码树为例,考虑限制译码节点的最大计算复杂度,设置译码节点所属叶节点中自由比特的数量小于等于4。结果如图1(b) 所示,固定4比特算法与SSCL 算法,译码节点均为d=2 这一码树层级。而FSCL 算法,译码节点则为图中蓝色节点,在码字前部提升至d=3。
FSCL 算法是一种通用的方案,考虑的是一般性的Rate-R 节点,关注其所属叶节点中自由比特的数量,具有普遍意义。同时观察极化码可靠度序列可知,可靠度较高的比特位置处于码字后部,而可靠度较低的位置处于码字前部。因此,当码字的码率较低,自由比特数量较少时,码字的前部呈现稀疏特性,使得码字前部的译码节点层级提升(可以接近于根节点),有效降低译码时延。
1.3 确信比特路径删减
通常在实际通信时,主要关注信道码字整体的误块率(Block Error Rate,BLER),极化码的码字BLER 可以表示为

是前i-1 个比特译对时第i个比特的错误概率,也可以认为是第i个比特的误比特率(Bit Error Rate,BER)的近似[24]。
极化码在编码时,根据可靠度序列由高到低,放置自由比特。而可靠度参数的实质为相应比特位置的最大似然译码错误概率上界[16]。由于极化特性,码字不同比特位置的可靠度往往相差非常大。仍以母码长度为N=16 的极化码为例,设定信噪比为0 dB,计算加性高斯白噪声信道的巴氏参数[25]。可以得到巴氏参数由低到高排在第1 位的值(表示最可靠)为0.000 3,而排在第8 位的值为0.260 4,几乎相差3 个数量级。如果提升信噪比,则巴氏参数值会相差更大。于是根据式(1)和(2)可知,可靠度较高自由比特的BER 对于码字BLER 几乎没有影响,码字BLER 主要取决于可靠度较低自由比特的BER。这种可靠度的极化特性可以用来降低译码的复杂度。文献[26]根据每个比特的巴氏参数得到BER,再转换为其相应的似然比阈值。采用SCL 算法译码时,如果叶节点信息比特的似然比高于阈值则不进行路径扩展,即回退到SC 算法。而对于固定4 比特算法,文献[27] 统计了4 个叶节点中连续出现高可靠信息比特的情况,并分别进行排序复杂度的简化。这两种方案,本质上是利用可靠度的极化特性对译码节点的路径扩展进行删减,但译码节点的位置没有改变,译码时延也没有从时序方面降低。
对此,将可靠度较高的自由比特称为确信比特(Trusted Bit),并应用于FSCL 算法中。在译码时,先根据自由比特中确信比特的数量进行路径删减,然后再根据剩余的自由比特数量进行路径扩展。这样,基于分阶段排序的思想减少了路径扩展的规模,降低了排序复杂度[28]。更重要的是,可以在不增加排序实现硬件资源的情况下,每次译码更多的比特,进一步的将译码节点上移。对比图1(a) 和1(b) 中的码树,图1(c) 中绿色节点表示确信比特。同样考虑限制译码节点的最大计算复杂度,设置译码节点所属叶节点中,自由比特的数量与其中确信比特数量的差小于等于4。由图中蓝色节点可以看到,采用结合确信比特的阈值判断之后,FSCL 算法的后部码字译码节点也提升至d=3 这一层级。
根据可靠度的极化特性,当码率较高时,自由比特数量较多,同时确信比特也会相应增加。这样结合前文所述,无论码字的码率高低,FSCL 算法都可以同时利用极化码的稀疏特性和极化特性,提升整体的译码节点,减少f/g函数的时序数,有效降低译码时延。
2 FSCL算法译码流程
考虑一般性,设码字母码长度为N=2n,由一个满二叉树表示,n为码树的层级。设码字中自由比特数量为K,其中确信比特数量为KTB,列表路径数为L。对于其中的节点v,其层级为dv,dv=n表示当前节点为根节点,dv=0 表示当前节点为叶节点,节点v所属的叶节点数量为2dv。设维度为2dv×1 的向量ξv为节点v所属叶节点中各类型比特位置标识。令向量α表示对数似然比(Log likelihood Ratio,LLR)信息,向量β是对应的比特,而向量p表示PM 值信息,具体向量的维度如后文所述。同时,设置码树节点的译码判决阈值为KTH。
译码流程实现步骤如下:
(1)译码过程由根节点开始,当前节点v的比特位置向量ξv中自由比特数为Kv,其中确信比特数为,于是定义路径扩展比特数。由其父节点传递的L条路径的LLR 信息,分别是L个维度为2dv×1 的向量。同时传递的L条路径的PM 值信息,由维度L×1 的向量pv表示。

其中,为母码码字长度为2dv的生成矩阵[2,6],即将原先叶节点到译码节点的比特更新递归整合成编码过程。对父节点传递来的L条路径分别进行上述比特向量扩展,其中第l条路径扩展出新的2Kv条路径相应的PM值为:

(3)如果KvEX>KTH,则不在当前节点v进行译码。提取节点v的比特位置标识向量的前半部分:

得到左子节点的比特位置标识向量。通过f函数计算,得到左子节点vLF的L条路径分别对应的维度为2dv×1 的LLR 向量:

在左子节点vLF完成译码流程之后,会将经过路径扩展和删减之后L条路径的信息返回至节点v,包括更新之后的L条路径PM 值向量,以及相应的比特向量。然后,通过g函数计算,得到右子节点vRT的L条路径分别对应的维度为2dv×1 的LLR 向量:


(4)当根节点完成译码操作之后,译码流程结束,输出译码结果。
3 仿真与分析
3.1 性能仿真实验
本文通过仿真实验对比了SCL、4b-SCL 与FSCL 三种算法的性能。其中4b-SCL 表示固定4 比特SCL 算法,同时FSCL 算法的译码节点阈值KTH设定为4 比特。为了对比简洁,设置仿真实验参数为加性高斯白噪声信道,调制方式为QPSK,译码路径列表数为L=8。考虑码率较低和较高的两个仿真用例,其具体参数设置如表1 所示。

表1 仿真用例参数
此外,考虑对译码节点的实现复杂度做一定的限制,设置FSCL 算法每次译码时译码节点所属叶节点中自由比特的数量不超过8 比特。为了更加清晰地描述确信比特对性能的影响,将确信比特数与自由比特数的比值定义为确信比例,即:

显然有ηTB∈ [ 0,1]。
图2 是关于case1 的BLER 性能的仿真。如图2(a)所示,SCL、4b-SCL 与FSCL 三种算法的性能是一致的。当确信比例ηTB提升到1/6 和1/3 时,在BLER=10-5性能处仍然没有损失;当μTB提升至2/3 时,出现较小性能损失。图2(b)验证了确信比特数对FSCL 算法性能的具体影响。固定SNR 值分别使得BLER 为10-1,10-2和10-3,可以看到,随着确信比特数的增加,BLER 先保持恒定,随后逐渐提高,到达一个数值之后会迅速抬升。而设置的BLER值越大,在保持性能恒定的条件下,可以选取的确信比特数也越多,这样可以更大程度的降低译码时延。

图2 BLER case1
图3 是关于case2 的BLER 性能的仿真。由图3(a)可知,SCL、4b-SCL 与FSCL 三种算法的性能是一致的。而且,确信比例ηTB提升至2/3 时,在BLER=10-4处仍然没有性能损失。图3(b)对确信比特数关于FSCL 算法性能的影响进行了验证。同样的,在固定BLER 相应的SNR 条件下,增加确信比特数,BLER 在保持一段的恒定之后,逐渐提高至一个数值后迅速抬升。同时可以看到的是,在相同的性能条件下,case2 可以设置的确信比例明显高于case1。

图3 BLER case2
由上述仿真可以看出,当自由比特越高,码率越高时,可以选取的确信比特数也越多。通过大量的仿真和统计分析,给出确信比特的经验公式如下:

其中,E表示传输码字长度,R=K/E是码字的码率。参数ω1,ω2,ω3,均为实数,可以根据不同的性能和时延需求进行调整,同时将结果进行向下取整。当需要保持的恒定性能为BLER=10-2时,可以给出推荐的参数配置为ω1=0.2,ω2=0.6,ω3=-6。这样,对于case1 可以得到确信比特数为9;而对于case2 可以得到确信比特数为54。当然,如果能够接受一定程度的性能损失,则可以配置更多的确信比特。
3.2 时延分析
在实际实现过程中,通常以时钟周期(Clock Cycle,CC)为单位来评估译码过程的时间复杂度,即完成译码必须要进行的时序数。对于以SCL 算法为框架的译码方案,码树中从根节点到译码节点之间每一个节点,进行f/g函数计算都需要各消耗一个CC[29]。以母码长度为N=2n的码字为例,对于SCL 算法,其译码过程的CC 数为[36]:

而对于4b-SCL 算法,译码节点提升两个层级,但同时由于译码节点的实现复杂度增加,因此需要消耗一个CC[30,31],于是可以得到其译码过程的CC 数为:

可以看到,SCL 算法与4b-SCL 算法的时延量级均为O(N),但4b-SCL 算法相对于SCL 算法时延降低超过两倍。
对于FSCL 算法,较难得到关于译码CC 数的理论表达式。如表2 所示,根据仿真实验的两个用例,对SCL、4b-SCL 和FSCL 三种算法的CC 数进行了统计。其中,由于FSCL 算法也是利用码树的结构,可以认为SSCL 算法与FSCL 算法(ηTB=0)的CC 相接近。可以看到,FSCL 算法的CC 数明显小于SCL 算法和4b-SCL 算法。随着确信比特的增加,CC 数量持续降低。虽然没有准确的闭式解,但可以近似认为,FSCL 算法的CC 数与路径扩展比特数有线性关系,即:

表2 译码CC数
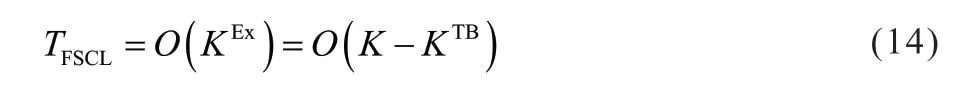
由上述分析可知,译码的计算复杂度主要取决于译码节点所属叶节点的比特扩展和路径排序。FSCL 算法正是利用码树的稀疏特性和极化特性,在保证性能的条件下有效识别出真正需要路径扩展的比特,从而提升译码节点层级,实现了高效低时延的译码器。
4 结束语
为了应对未来6G 系统超高可靠低时延的要求,本文提出FSCL 算法译码方案,可以通过调整确信比特的比例,灵活实现译码性能和译码时延的自适应优化,较好地适用于URLLC 场景的业务需求。
极化码在5G 时代进入标准,作为控制信道和广播信道的编码规范,已经证明其巨大的工程实用价值。而对于进一步应用于数据信道,相应的前瞻性研究已经开展。在数据传输方面,与多天线技术和非正交多址技术相结合,可以获得更高的频谱效率和更大的系统容量[4]。同时,基于混合自动重传请求机制,可以根据信道条件实现链路自适应传输[32,33]。而在译码方案方面,基于可靠度的排序统计译码算法(Ordered Statistic Decoding,OSD)可以获得短码时近似最大似然译码的性能[34]。同时,也可以采用并行译码架构的置信传播算法(Belief Propagation,BP),获得在低信噪比条件时译码性能的提升[2]。但OSD 算法需要解决复杂度高的问题,而BP 算法需要降低在高信噪比时的误码平层[10]。
随着相关技术研究的逐渐成熟,极化码的潜力和优势也被不断的发掘出来。极化码提出至今仅十余年,作为5G 的编码标准只是其实用的开始。相信在未来的6G 时代,极化码将具有更加广阔的应用前景。

