平行泊车路径规划与跟踪控制研究

魏双叶，童亮,2

(1.北京信息科技大学 机电工程学院，北京 100192；2.北京信息科技大学 北京电动车辆协同创新中心，北京 100192)

0 引言

随着汽车数量的不断增长，停车位紧缺且空间越来越狭小，泊车导致的事故也在增多，而自动泊车系统可以自动控制方向盘和车速，快速地完成泊车操作，解决停车入位的问题[1-3]。

关于自动泊车系统的研究，Walambe等[4]以车辆速度和前轮转角为控制输入，以位置坐标为控制输出，设计了模糊控制算法控制车辆实现自动泊车。Qin等[5]设计了一种比例—积分—微分(PID)控制算法实现自动泊车。Song[6]和叶浩[7]等设计了一种输入方向盘转角和车轮速度得到实际运动轨迹的模型预测控制器(model predictive control，MPC)。从现有研究可知，传统的模糊控制和PID控制具有结构简单、鲁棒性强的优点，但存在响应慢、精度低的问题。MPC可有效解决控制约束和多目标优化的问题，但对于智能车辆的路径跟踪控制仍存在不足。

本文在假设已经获得了关于停车位周围环境全部信息的基础上，研究了路径跟踪控制问题。通过逆向行驶的方法进行三段式泊车路径规划，并对其进行五次多项式平滑处理，实现了泊车过程的连续性。最后采用模型预测控制与PID控制结合的方法，达到了很好的跟踪效果。

1 汽车运动学模型

通常自动泊车时车辆行驶速度相对较低，不会发生横向滑动，可以忽略汽车的侧向力，且汽车没有车轮侧滑角，此时汽车满足阿克曼转向几何原理[7]。因此，以汽车等效前轴偏转角度和后轴中心点坐标为研究目标，本文应用图1所示的汽车运动学模型[8]，并在此基础上研究了平行泊车系统跟踪控制方法。

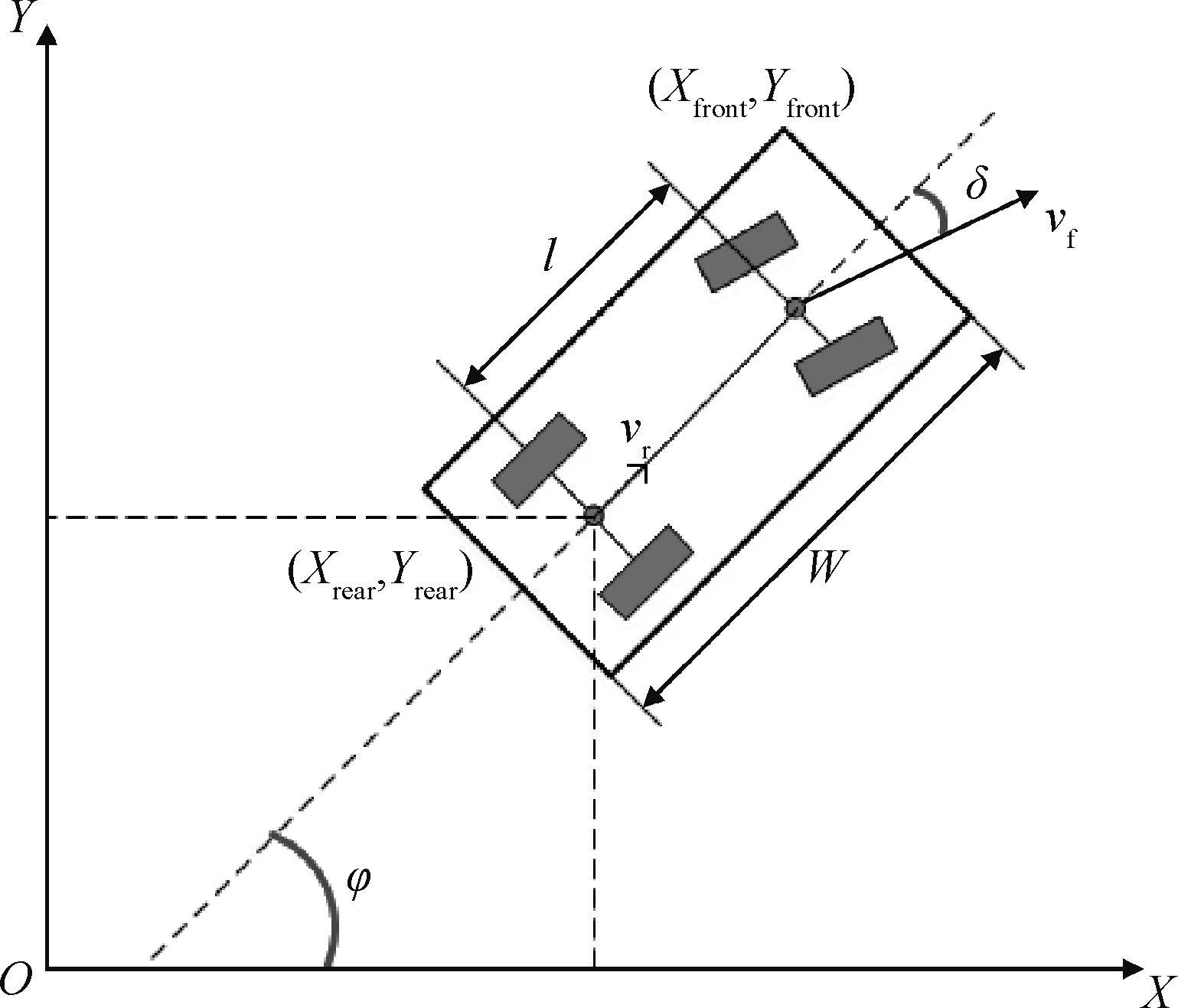
图1 汽车运动学模型

图中(Xrear,Yrear)和(Xfront,Yfront)分别为汽车后轴和前轴中心坐标，vr和vf分别为汽车后轴和前轴中心速度，W为车辆宽度，φ为汽车横摆角，δ为前轮偏角，l为轴距。

假设汽车转向过程中质心侧偏角恒定，则泊车过程中汽车运动学模型为

(1)

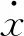
2 平行泊车路径规划

2.1 泊车过程分析

针对狭小平行停车位自动泊车，为使泊车路径曲率连续，缩短泊车时间，本文采用了圆弧—直线—圆弧三段式泊车，泊车路径如图2所示。

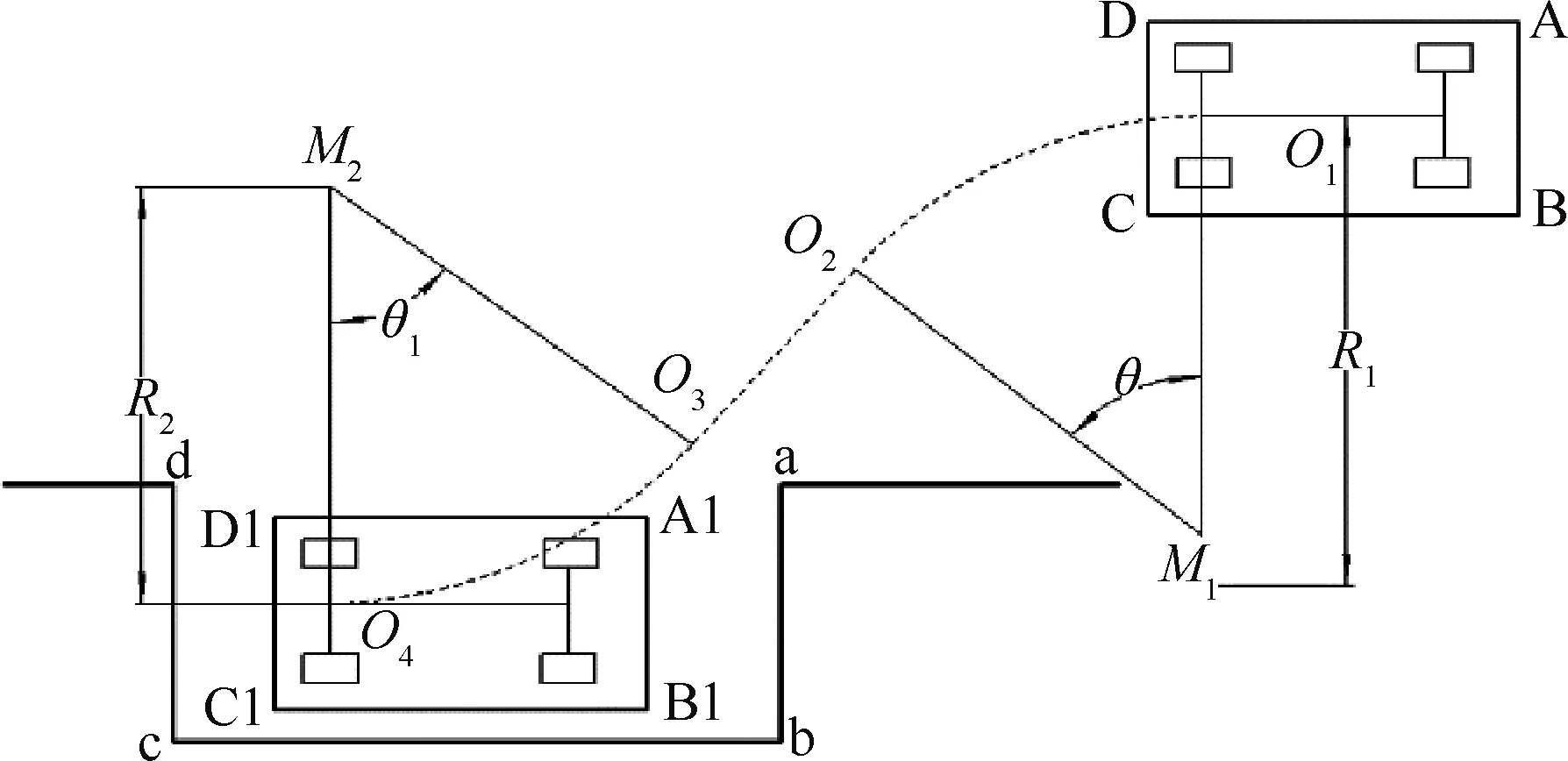
图2 平行泊车路径

设汽车以速度v匀速泊车，为便于车位探测，假设汽车的初始姿态与停车位方向平行，汽车后轴中心的泊车初始位置记为O1点。平行泊车过程即目标车辆从初始位置O1点以R1为转动半径、M1为转动中心转动θ角度后行驶至O2点；然后车辆沿直线O2O3行驶至O3点；最后车辆从O3点以R2转动半径、M2为转动中心转动θ1后行驶至O4点，泊车结束。

考虑到平行泊车过程中受到的碰撞约束和汽车约束，根据泊车环境和车辆尺寸信息，通过逆向行驶的方法可确定泊车关键点坐标、所需最小停车位尺寸以及初始停车范围，满足要求则可进行泊车。

2.2 路径平滑处理

圆弧—直线—圆弧平行泊车路径规划方法可能存在路径不够平滑的问题，且考虑到其他的平滑处理方式可能存在求解参数多、计算量大或者加速度不连续等问题，本文利用五次多项式曲线拟合对初始路径进行了平滑处理。

假设泊车路径表达式如下：

Y=K1X5+K2X4+K3X3+K4X2+K5X+K6

(2)

式中：K1～K6为五次多项式各项系数。

已知6个约束条件：泊车规划路径经过泊车起点、终点、O2和O3点；在泊车起点与终点处，泊车路径的导数应为0；为使汽车初始状态的等效前轮转角为0，汽车在泊车轨迹初始位置的二阶导数也应为0。可求解出多项式系数K1～K6，从而得到平滑处理后的泊车轨迹方程。

3 路径跟踪控制器的设计

本文采用了PID控制汽车车速、MPC控制前轮转角的控制策略。

3.1 模型预测控制基本原理

由式(1)汽车运动学模型可知，自动泊车系统可以看作是一个输入为控制量u(v,δ)、状态量为χ(x,y,φ)的控制系统[9-10]。可表示为

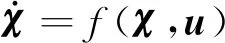
(3)

由汽车后轴运动轨迹表征泊车参考路径，用r表示参考量，一般形式为

(4)

式中：ur=[vrδr]Τ，χr=[xryrφr]Τ。

对式(3)在参考轨迹点进行泰勒级数展开，可得：

(5)

将式(5)与式(4)相减，可得线性化的汽车误差模型：

(6)

为将该模型应用于MPC控制器，对式(4)进行离散化处理得：

(7)

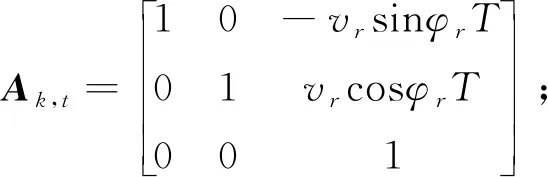
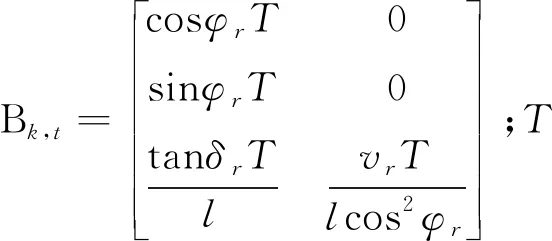
采用目标函数：

(8)

式中：η为模型预测值；t为采样时间；NP为预测时域；NC为控制时域；ρ为权重系数；ε为松弛因子；Q和R为权重矩阵；ΔU为控制增量矩阵[9-10]。

该系统控制量和控制增量的极限值分别为：

umin(t+k)≤u(t+k)≤umax(t+k),k=

0,1,…,Nc-1

(9)

Δumin(t+k)≤Δu(t+k)≤Δumax(t+k),k=0,1,…,Nc-1

(10)

考虑到约束条件，将目标函数转化为标准二次型，解决以下优化问题：

(11)

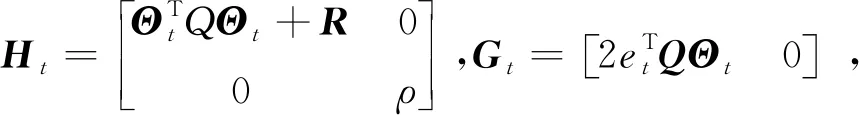
完成控制周期内的计算后，即可求得控制输入增量：

(12)

将控制序列中第一个元素应用于系统，得到：

(13)

通过重复以上控制过程，完成对参考路径的跟踪控制。其中，通过纵横向跟踪能力测试可以获得约束条件中涉及的参数。

为验证在泊车系统路径跟踪中模型预测控制器的可行性，根据式(4)及车辆外形参数，本文在 Matlab/Simulink中搭建了如图3所示的模型预测仿真模型。其中，控制器输入为汽车实际横向位移、纵向位移和横摆角速度，输出为汽车实际车速和实际前轮转角。

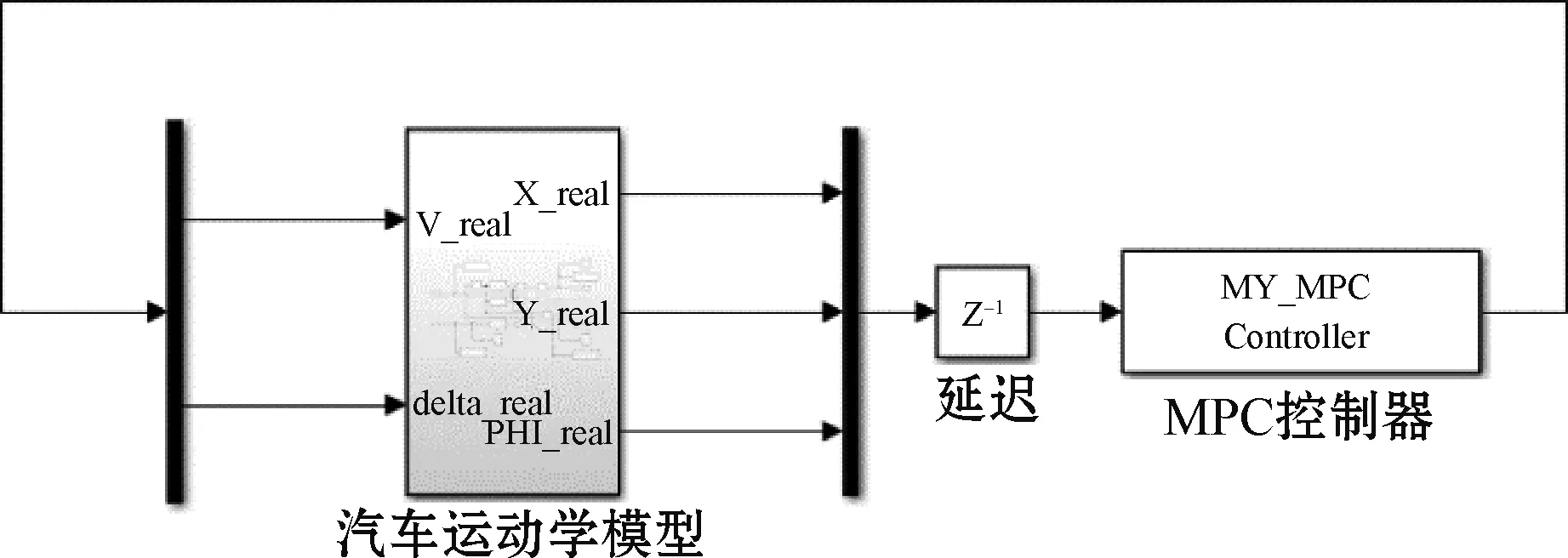
图3 模型预测仿真模型

3.2 路径跟踪控制器的优化

考虑到PID控制具有结构简单、鲁棒性强的优点，而MPC可实时修正控制误差、有效解决控制约束和多目标优化的问题[9-11]，本文提出了PID控制和MPC相结合的控制策略，并搭建了如图4所示的路径跟踪控制器模型。

图4 路径跟踪控制器模型

其中，PID控制器输入为期望车速和MPC控制器输出车速，输出为PID控制下汽车纵向车速。MPC控制器输入为汽车实际横向位移、纵向位移和横摆角速度，输出为MPC控制下的车速和前轮转角。通过两种控制策略结合，使得汽车速度保持恒定，跟踪控制精度得到提高。

4 平行泊车仿真验证

4.1 路径规划结果

设停车位长为6 m，宽为2.3 m，道路宽为3.5 m。在Matlab中进行路径规划和平滑处理，结果如图5所示，图6为平滑处理后路径的导数。

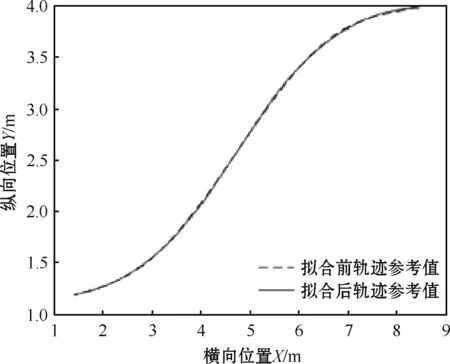
图5 参考路径

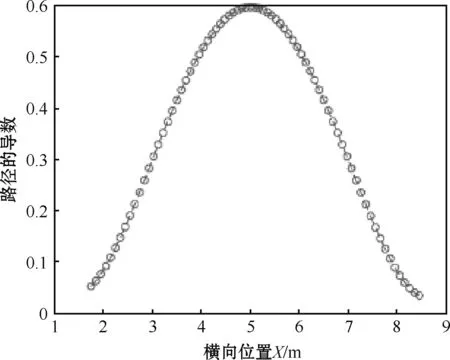
图6 规划路径的导数

从图5可以看出，处理后的泊车路径能够平滑地连接泊车起点与终点。由图6可知，泊车起始点与终点的导数分别为0.05和0.03，可认为泊车起点与终点的位置满足设计要求。

4.2 MPC与PID控制策略对比

选择图5中拟合后的路径作为泊车参考路径，本文在 Matlab/Simulink中对MPC和PID控制器进行了分析比较，仿真结果如图7、图8所示。

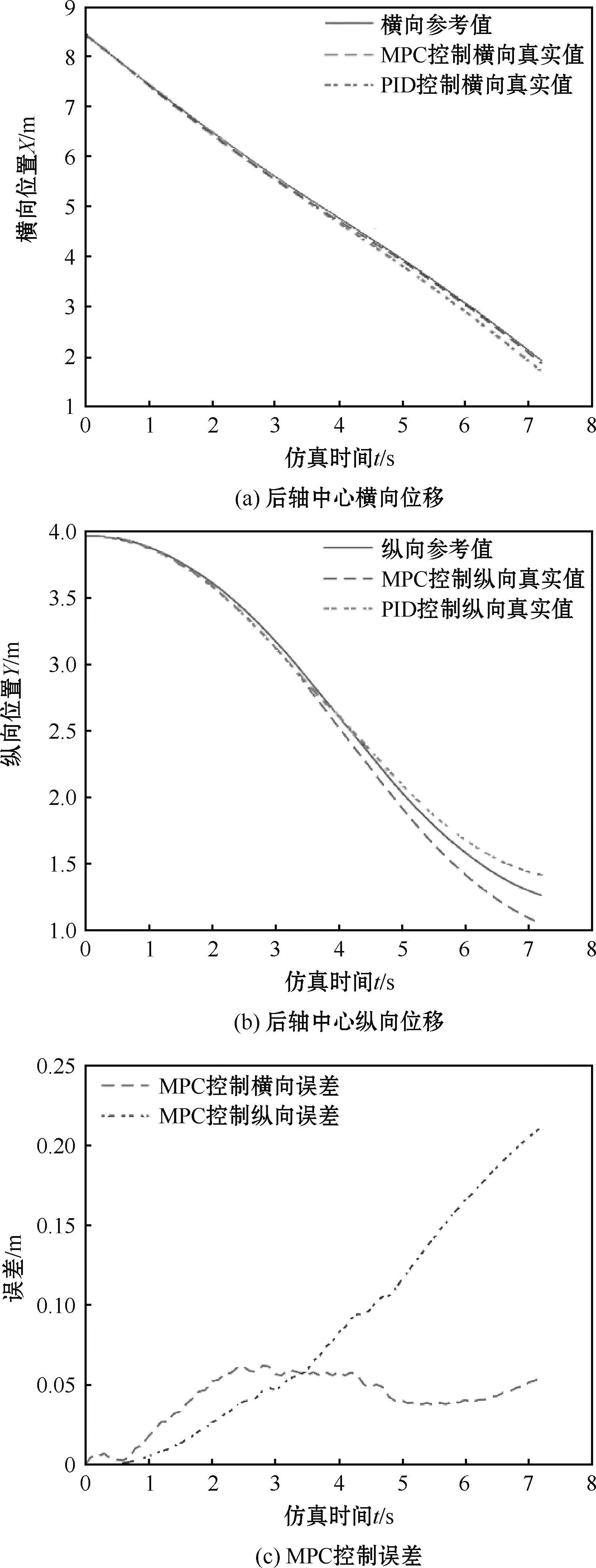
图7 路径跟踪对比

图7(a)、(b)分别是泊车过程中两种控制下的横向位移与纵向位移，可以看出两种控制方法均可以跟踪期望轨迹。图7(c)、(d)分别是MPC控制和PID控制下的位移误差，可以看出，泊车结束时，MPC控制下的横向和纵向误差分别是0.052 m、0.212 m，PID控制下的横向和纵向误差分别是0.242 m、0.146 m。结果表明，MPC控制下的横向位移误差远小于PID控制下的横向误差，且两者的纵向位移误差相差不大。对比可知，MPC跟踪效果更好。

4.3 跟踪控制器优化后效果验证

由4.2节可知，模型预测控制效果整体优于PID控制，但仍存在一定误差。设泊车速度为-1 m/s，利用优化后的控制器进行泊车控制，跟踪结果如图8～10所示。

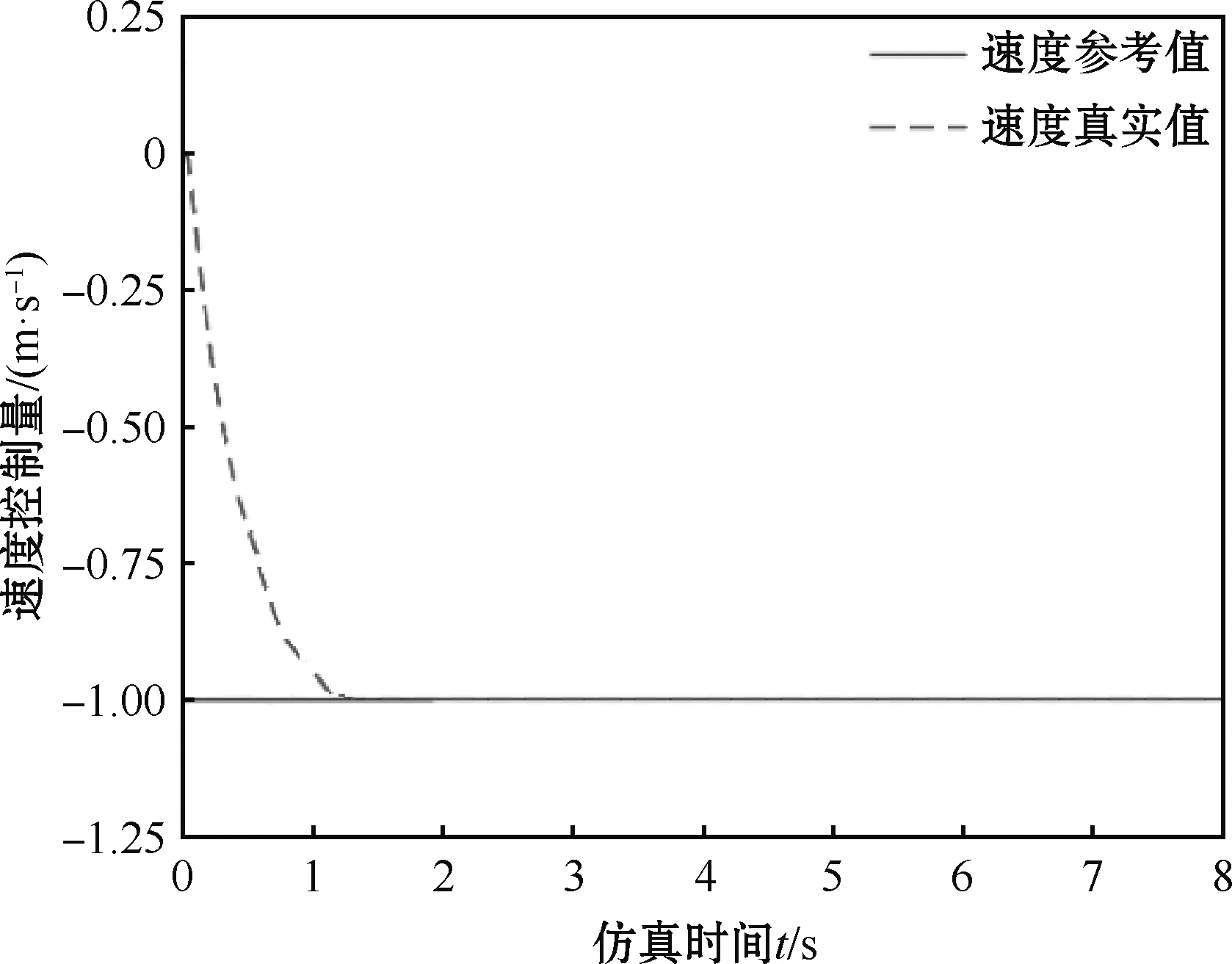
图8 车速控制器仿真结果

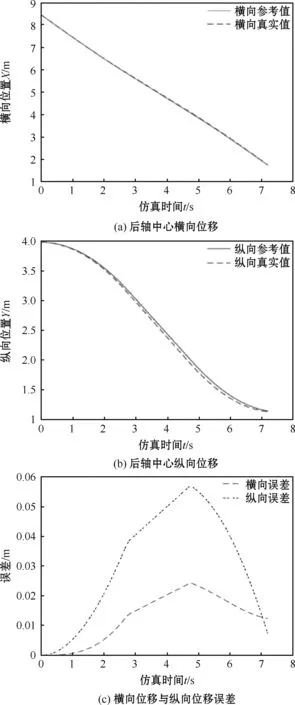
图9 路径跟踪效果

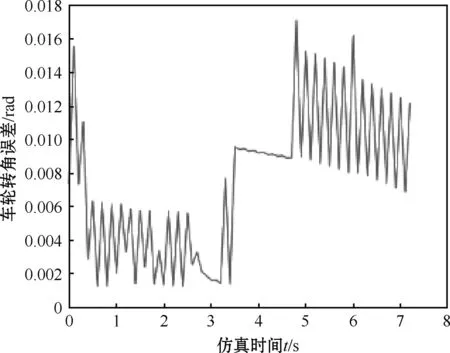
图10 车轮转角控制量

图8为车速控制器仿真结果。可以看出，1.3 s后车速可保持在期望值-1 m/s,没有产生超调和波动，说明PID控制能稳定控制车速，且效果较好。

图9为路径跟踪效果图。从图9(a)、(b)可以看出，后轴中心位移与参考路径基本重合。从图9(c)可以看出，虽4～5 s时跟踪误差较大，但均不超过0.06 m。且泊车结束时，车辆后轴中心点与目标位置存在的误差很小，横向与纵向误差分别是0.012 m和0.008 m。

图10为车轮转角误差。可以看出，车轮转角误差不超过0.02 rad，可认为跟踪精度较高。

与原MPC控制器比较可知，后轴中心的横向位移误差降低了0.037 m，纵向位移误差降低了0.204 m。虽然车轮转角变化不明显，但从位移误差可以看出，该方法提高了控制精度，可以得到更好的控制效果。

5 结束语

本文利用逆向行驶的方法进行平行泊车路径规划，并对该路径进行了五次多项式平滑处理。然后将模型预测控制器与PID控制器进行了比较分析，提出了PID控制速度、MPC控制前轮转角的控制策略，并在 Matlab / Simulink中进行平行泊车仿真验证。结果表明，该控制策略可以使车速恒定，跟踪误差减小，具有很好的跟踪控制效果。