基于时间序列的季节性气温预测研究

赵成兵，刘丹秀，谢新平，刘 静

（安徽建筑大学 数理学院，安徽 合肥 230601）

气候变化对人类活动产生重要的影响，研究气候非常有必要。随着大数据时代的到来，为气象预报提供了更加科学的技术支持。由于气象数据与时间紧密相关，因而可以采用时间序列的方法对气象数据进行处理及分析。目前对于时间序列研究主要分为三个方面[1-2]：一是传统统计模型包括线性模型、自回归移动平均模型（ARIMA）等。如Dimri 等[3]使用季节性ARIMA 拟合气温单变量模型，达到很好的拟合效果；谭小花[4]用随机分析法对重庆市气温数据做了趋势分析，选用季节指数和ARMA 模型对序列拟合预测，发现采用季节指数能更好地拟合趋势并预测未来序列。二是构建机器学习模型。朱晶晶等[5]依据CMSVM2.0 函数估计和交叉验证等方法，利用月平均气温建立了SVM 回归预报模型，发现交叉验证下的模型预测效果更好；张曼玉[6]对长三角地区的日温差进行了随机森林拟合，发现影响温度差的主要因子是地表温度；陶晔等[7]利用随机森林筛选出与气温变量高度相关的因子，将这些因子带入长短期记忆网络中，建立了预测性能更佳的RF-LSTM 模型；王可心等[8]将输入特征进行复合，引入复合特征随机森林回归模型，并用袋外误差率调试参数，发现雨雪天气状况下的路面温度预报精确度最高。三是以各种方式将统计模型与机器学习模型结合起来的混合模型。门晓磊等[9]使用岭回归，随机森林和深度学习三种方法分别对逐日地面2 m 处的气温进行预报，发现三种方法预测能力相差不大，甚至在小数据集上，随机森林和岭回归可能优于深度学习方法；曾静[10]将输入变量进行多项式扩充，再采用回归方法和随机森林等方法，得出最优拟合温度订正模型，再利用长短期记忆模型建模，最终建立多气象因子模式的温度预报模型；卢维学等[11]提出了基于随机森林算法的偏最小二乘回归模型，通过比较发现该回归模型的稳定性和预测精度优于其他模型。

在已有的研究中，随机森林模型拟合气温时序数据将原始数据直接作为输入特征，或者将输入特征进行组合，作为复合特征引入模型，忽略了气温数据中存在的季节性特征。本文将月份信息分类并采用One-Hot 编码，提取数据中的季节性，作为随机森林模型的输入特征，构建模型参数组合。在此基础上，利用随机搜索和网格搜索对季节性模型中的超参数进行进一步优化；最后计算拟合误差和准确率[12]，并和乘积季节ARIMA 模型预测能力进行比较。

1 模型设计

1.1 ARIMA 模型

ARIMA 模型的基本思想是通过变换去除序列的趋势，使非平稳序列变成平稳序列[13]。ARIMA模型的AR 部分是根据研究变量自身的历史值进行回归，MA 模型则是出现在不同时间间隔的历史误差值的线性组合。

对于存在季节性的时间序列，季节性可能对建立的模型有影响，因而需要建立季节模型，该模型包括季节影响和非季节影响。季节ARIMA 模型记为SARIMA（p，d，q）（P，D，Q），其 中，P，D，Q 表示模型季节性部分。本文采用季节性ARIMA 模型进行建模，主要建模步骤为：首先观察数据时序图，当观测到序列具有趋势或异方差时，则对其进行变换或差分，去除趋势，稳定方差，直到变换后的数据满足平稳性检验的条件，然后根据最小信息量准则和贝叶斯信息准则，拟合预测模型。

1.2 随机森林

随机森林算法是监督学习算法的一个分支，使用集成学习方法回归，集成学习方法主要包括神经网络、SVM 和决策树。随机森林采用Bagging Bootstrap 技术，通过随机抽样产生更多的样本。在Bagging 技术中，每个模型都独立运行，且最终输出的是汇总后的模型。但决策树可能会出现过拟合现象，且预测值对训练数据过于依赖和敏感，因而应用随机森林回归作为大决策树的组合，以此代替决策树。随机森林中构建的树并行运行，没有任何交互，其基本思想就是结合多个决策树确定最终结果，而不是依赖单个决策树。

文中随机森林算法的过程可以总结为如下步骤：

（1）对数据进行预处理，提取并编码季节信息；

（2）划分数据集，将其分成训练集和测试集；（3）对抽样的训练集建立回归树模型，汇总多棵回归树的结果，取其平均作为最终预测结果；

（4）采用两种搜索方法对训练模型进行超参数的优化。

1.3 预测能力评估

1.3.1 平均绝对误差（MAE）定义如下：

其中，n 为预测的时间点步长，fi为预测值，yi为实际观测值。实际观测值与预测值差值越接近，误差越小，说明预测模型的准确性越佳。

1.3.2 平均绝对百分误差（MAPE）

定义如下：

MAPE 越接近于零，表示模型预测的精度越高；若MAPE 大于100%，说明预测模型为劣质模型。

2 实证分析

2.1 数据来源

本文中数据来自中国气象数据网，数据包括合肥市某站点观测到的每月平均最高温度（A_MAX_T）、平均最低温度（A_MIN_T）、日照时数（sunshine_duration）、最高温度（MAX_T）、最低温度（MIN_T）、平均温度（AT）、降水量（precipitation）和月份（Month）八个指标，涵盖了1988 年1 月至2020 年9 月的各月数据，数据无缺失值。

2.2 季节性ARIMA 模型的应用

2.2.1 差分运算

差分运算是一种提取序列中确定性信息的方法，适当的差分便可以充分提取信息。

季节性ARIMA 模型是处理时间序列的流行模型之一，它将数据具有的季节性特征考虑到预测中，需要观察自相关系数图（ACF）和偏自相关系数图（PACF）并依据赤池信息准则或贝叶斯信息准则选择合适的模型。因为平均气温序列中含有季节效应，故采用季节模型进行拟合，选取1988 年1 月到2019 年12 月的平均气温月度数据作为训练集，利用拟合的模型预测2020 年1 月至2020 年9 月的每月平均气温数据，并和真实值做对比，计算预测准确度，建模过程通过R 语言实现。

图1 是平均温度时序图。其中，横轴表示日期，从1988 年1 月至2019 年12 月；纵轴表示实际观测的月平均气温值，单位为℃。由图可见，随着时间推移，温度值呈现上升后下降的循环，具有很强的周期性，且无明显增加或减少的趋势，序列平稳。

图1 平均温度时序图

图2 是气温序列延迟60 阶的自相关系数图与偏自相关系数图，横轴表示延迟阶数。左侧图中，纵轴表示的是序列的自相关系数；右侧图中，纵轴表示偏自相关系数。由图可知，左图表明ACF 呈现正负值交替的趋势，且延迟60 阶后，自相关系数无衰减趋势，表现为拖尾性；右图显示在延迟12 阶后，PACF 落入两倍标准差范围内，呈现截尾，表明平均气温序列间具有自相关性。

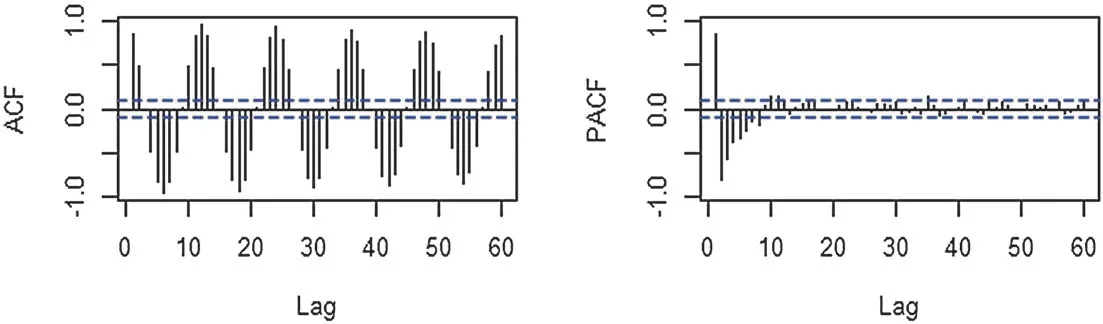
图2 自相关系数图与偏自相关系数图

由于序列存在自相关性和季节性，故对原序列作1 阶12 步差分，即差分后新序列值为∇12xt= xt- xt-12，其中 xt为序列值。12 步差分后的序列如图3 所示，温度值均在零值温度线上下波动。为检验序列是否平稳，对差分后的序列进行单位根检验，结果显示P=0.01，小于显著性水平0.05，表示不接受原假设，即差分后的平均气温序列中不存在单位根，认为差分后序列基本平稳。

图3 平均温度12 步差分后时序图

如图4 所示，虽然延迟12 阶的自相关系数显著不为0，偏自相关系数在延迟12 阶，24 阶显著不为0，但自相关系数与偏自相关系数基本在2 倍标准差范围内。

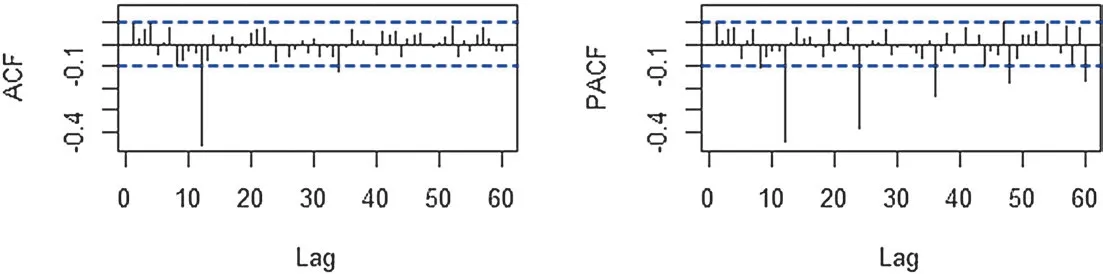
图4 平均温度差分后自相关系数图与偏自相关系数图

2.2.2 模型建立

根据上图可得，自相关图显示延迟12 阶自相关系数显著大于2 倍标准差范围，偏自相关系数图也是如此，说明序列仍然蕴含显著的季节效应，尝试拟合简单ARMA 模型，但效果并不理想，考虑该序列具有的短期相关性和季节性，尝试用乘积模型拟合序列的趋势。

首先考虑序列12 阶以内的自相关系数和偏自相关系数均不截尾，尝试使用ARMA（1,1）模型提取差分后序列的短期自相关信息；其次自相关图显示延迟12 阶的自相关系数显著非零，但延迟24 阶自相关系数落入两倍标准差范围内，偏自相关系数显示延迟24 阶以后的偏自相关系数显著非零。故以12 步为周期，构建ARMA（0,1）12，经过多次调整之后，依据AIC，BIC 准则最终确定拟合的模型为ARIMA（2,0,1）（0,1,1）12，此时BIC 值与AIC 值达到最小。

2.2.3 模型检验

图5 是差分后序列的残差自相关检验结果，可以发现，自相关系数呈现逐步衰减趋势，存在小幅度波动，但均在两倍标准差范围内，说明残差序列自相关性弱。同时纯随机性检验表明：12 步差分后的序列残差在滞后6 期时，P=0.962 1；当滞后12期时，P=0.85；当滞后24 期时，P=0.782 9，所有的P值均大于显著性水平0.05，表明不拒绝原假设，即差分后的序列的残差独立，模型通过残差白噪声检验，说明拟合的乘积季节性模型ARIMA（2,0,1）（0,1,1）12有效。

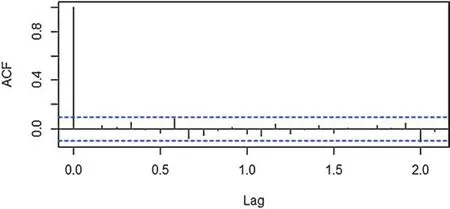
图5 差分后序列的残差自相关图

2.2.4 模型预测

表1 中给出了预测值与实际观察值的数据，并计算了预测误差。可以看到仅有个别温度点的预测值与实际值差异较大，最大温度预测误差为3.97℃，最小预测误差为0.08℃，经过计算可以得出：

表1 预测值与真实值对比

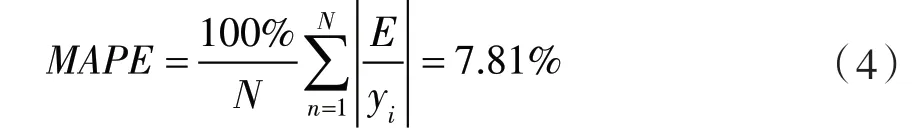
即使用拟合模型预测准确度可以达到92%以上。

2.3 随机森林分析

2.3.1 数据预处理

本文采用Python 语言编写，基于Sklearn 环境下构建随机森林模型，样本集中包含393 个样本，其中70%划分为训练集，剩余30%作为测试集。在对数据进行初步分析后，发现气象时序数据存在季节性特征，而冬季与夏季的温度差距很大，仅仅考虑月平均气温，精度是不充分的，所以使用文本特征提取方法，将季节性特征也纳入输入特征。春、夏、秋、冬四个分类变量是无序的、离散的，将这些特征数字化时，如果简单分类为1、2、3、4，分类变量之间便产生了顺序，且不能直接放入机器学习算法中，故而使用One-Hot 编码。

One-Hot 编码，又称一位有效编码，主要对M种状态进行编码，每个状态都有自己独立的寄存器位，并且在任意时候只有一位有效。即每个样本的M 种属性中只能有一个为1，表示该样本的该属性属于这个类别，其余扩展属性都为0。具体编码过程如下：

根据季节特征，将十二月、一月、二月归类为冬季；三、四、五月归类为春季；六、七、八月归为夏季；剩余三个月份归为秋季。

即 Sqi=（春季，夏季，秋季，冬季）=（0，1，0，0），若i 为夏季，则形式如表2：

表2 One-Hot 编码规则

如果输入样本 xi是夏季，则以( xi,0,1,0,0)的形式采样。

2.3.2 对比实验

随机森林中包含大量的参数，如随机森林决策树的数目、树的最大深度，本文的数据量并不大，故将最大深度设置为None。节点最小分裂所需样本个数是某节点样本数的最小值，当节点样本数小于该值时，不会将其划分。叶子节点最小样本数代表的是叶子节点最少的样本数目，若小于该值，则该节点会被剪枝。为了验证季节性特征是否利于提高随机森林模型预测精度，本文用简单随机森林模型和季节性随机森林模型进行比较，从平均绝对误差、均方误差和准确度三方面衡量预测能力。

如表3 显示，在决策树的个数M 均为20 的前提下，简单随机森林模型的平均绝对误差为0.28，平均绝对百分误差是4.04%；而季节性模型所得出的平均绝对误差是0.26，平均绝对百分误差为3.86%，说明加入季节性特征之后，减小了模型误差，提高了预报准确度。与两种随机森林算法相比，乘积季节性ARIMA 模型预报气温误差更大，而且需要通过ACF 图和PACF 图主观确定模型的阶数，预测气温的准确率相对较低。

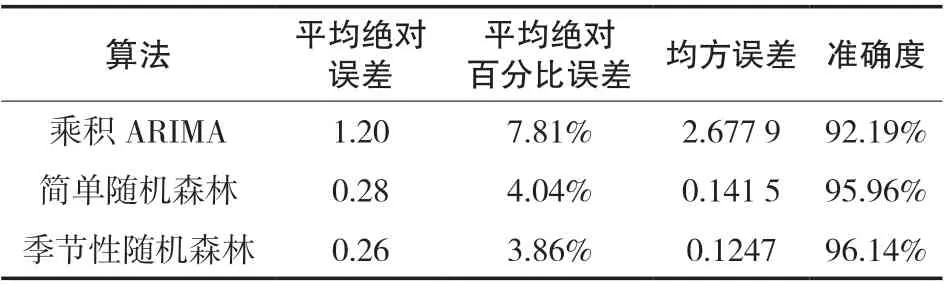
表3 各模型在月平均气温的预报性能对比

下图是测试集包含的118 个样本的真实标签值与预测值折线图，其中红色线表示预测值，绿色线表示标签值。可以看到，使用季节性随机森林模型进行预测，虽然有部分极值点的温度预测值与标签值存在偏差，但整体趋势一致，且准确度可以达到96%以上，总体预测效果较好。

2.3.3 参数优化

（1）网格搜索

超参数搜索算法一般包括目标函数、搜索范围等要素。网格搜索通过搜索上下限内的所有点确定最优值，因而极有可能找到全局最优值，但局限性在于计算量较大、耗时耗力，特别是需要调优的超参数较多时。一般先使用较广的搜索范围和较大的步长，寻找全局最优值可能的位置，然后逐渐缩小搜索范围和步长，寻找更精确的最优值。

（2）随机搜索

与网格搜索相比，随机搜索在上下限内随机选取样本点，搜索时间相对缩短，但产生的结果不一定是全局最优。当样本点集足够大时，随机采样也能找到全局最优值或其近似值。

在树的初始数目设为20 时，季节性随机森林模型预测精度可以达到96.14%，在此模型上进行超参数优化，并且使用三折交叉验证将数据集划分训练集和测试集，即将原始数据集进行三次划分，多次训练，取三次输出结果的均值作为算法精度的估计值，避免只将数据集一次划分而得出错误结论的情况。然后在季节性随机森林产生的最优参数空间基础上进行随机搜索。

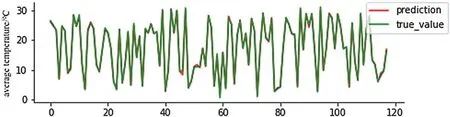
图6 真实值与预测值对比图

从表4 中可以看到，在Bootstrap 方法下，随机搜索最佳模型在树的个数为200、节点最小分裂所需样本数为2 时得到，此时准确率已经达到96.42%，优于树的个数N 为20 时的季节性随机森林模型。继续根据随机搜索产生的最佳参数空间，分别向最佳组合的左、右进行网格搜索，搜索的参数空间设定为N 取50，100 或150 时，节点最小分裂所需样本数取1，2 或3，同样使用Bootstrap 采样。结果显示，在树的个数为150 时，搜索到最佳组合，准确度为96.34%。结果未寻找到更优的参数组合，继续向右搜索。

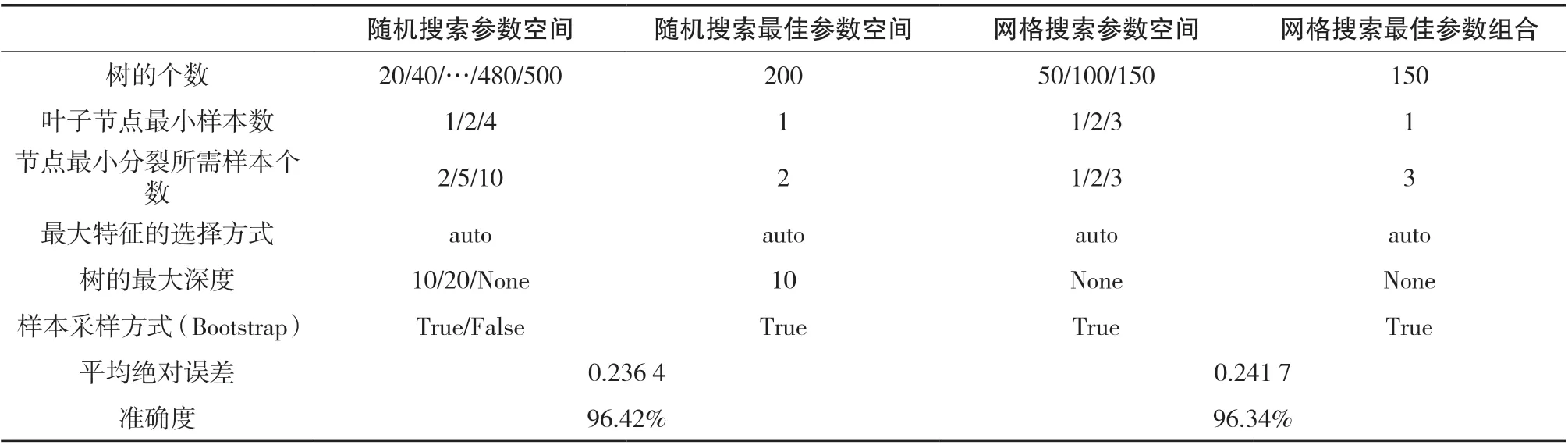
表4 随机搜索与网格搜索参数空间

表5 结果表明，在三折交叉验证下，当树的个数为100、节点最小分裂所需样本个数为2、叶子节点最小样本数也为2 时取得最优，此时预测准确率是96.45%，准确度进一步提升。

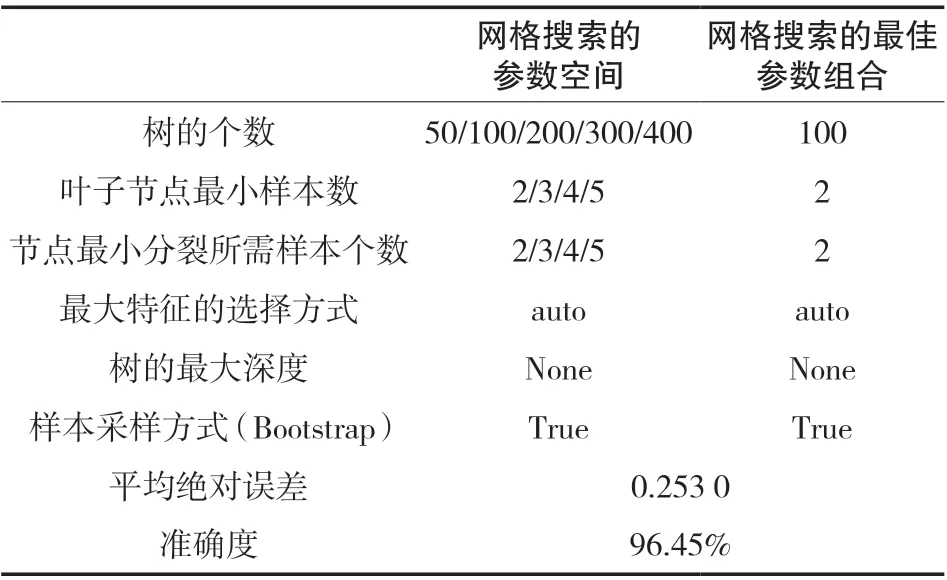
表5 向右网格搜索参数空间

3 结论

气候对人类的生活会产生巨大的影响。本文使用了基于R 语言的季节性ARIMA 模型和基于Python 语言的季节性随机森林两种模型对气象时间序列数据进行分析与建模，并对未来时刻进行了预测，得到如下结论：

（1）季节性ARIMA 模型可以很好地拟合时序数据中的季节性，预测精度超92%。虽然夏季高温极端值预报偏高，但偏差绝对值基本在3℃以内，认为预测效果有效。

（2）文中建立的随机森林模型引入季节特征作为输入特征时，模型对于温度极值的预测值偏小，整体拟合趋势符合实际趋势，且预测效果优于季节ARIMA 模型。

（3）在季节性随机森林模型基础上，利用随机搜索找出优化组合，然后根据该参数空间，在该组合附近进一步使用网格搜索，搜索该区域内所有可能值确定最优参数组合，此时模型的预测精度最高。

引入季节性特征的随机森林模型可用于气温预测，且预测误差较小。但由于资料限制，实验中数据仅是单个气象站的数据，输入变量较少，未能考虑到将周围地理气象数据可能存在的影响，这也是下一步研究的方向。