一类变系数回火分数阶扩散方程离散格式的收敛性分析

屈 威，叶宇航

（韶关学院 数学与统计学院，广东 韶关 512005）

回火分数阶扩散方程是分数阶扩散方程的推广［1］.在实际应用中，通常采用指数的回火得到回火的幂律跳跃步长（空间回火分数阶导数）和回火的幂律等待时间（时间回火分数阶导数），其在各类力学与物理行为、反常扩散［2］、欧式期权定价［3］等领域被广泛的应用.

近年来，关于回火分数阶偏微分方程的数值方法得到了广泛地研究.Li和Deng提出了回火加权移位Grünwald差分算子，并结合Crank-Nicolson（C-N）方法导出求解常系数Riemann-Liouville（R-L）回火分数阶扩散方程的数值格式，证明了数值格式在时间及空间方向都是二阶收敛［4］.随后，Qu和Liang将其结论推广到一类变系数的情形，并给出了数值格式的稳定性和收敛性分析，但收敛性证明所要求的条件较为严格，部分数值实验表明，当收敛性条件不满足时，数值离散格式仍能达到二阶收敛性［1］.为了获得更高精度的数值算法，文献［5-7］利用移位回火Grünwald差分算子构造出了具有三阶精度的回火差分算子以及高阶拟紧算子逼近正规化R-L回火分数阶导数，并利用所构造的高阶拟紧算子离散具有漂移项的单侧正规化回火分数阶扩散方程，同时，给出了数值离散格式稳定性和收敛性的理论分析.此外，对于Riesz回火分数阶扩散方程也得到了相应地研究.如文献［8-9］，分别基于新的生成函数，提出了二阶Lubich回火差分算子并结合（2，2）Padé逼近Riesz回火分数阶（阶数大于0小于2）导数，进而得到求解Riesz回火分数阶扩散方程新的数值离散格式，基于新格式的稳定性和收敛性也做了相应的分析.此外，文献［10］利用隐式中点法结合Lubich回火差分算子对带有满足Lipschitz条件的非线性源项的Riesz回火分数阶平流-扩散方程进行离散，并证明了格式的稳定性和收敛性.同时，多个数值实验验证了以上理论结果及所得数值格式的稳定性和收敛性的正确性.

笔者主要研究一类变系数回火分数阶扩散方程有限差分离散格式的收敛性，并对文献［1］中关于离散格式收敛性证明做进一步的扩展.具体地，对离散格式进行等价转换，利用合同矩阵的性质，给出了离散格式中系数矩阵不限定在负定性这一条件下的收敛性分析.笔者提出的收敛性证明方法和已有的研究成果相比，需要的条件较弱，具有更广的适用范围.考虑带有狄利克雷（Dirichlet）齐次边界条件的α阶（1＜α＜2）变系数回火分数阶扩散方程：

其中a，b和T已知，回火参数λ为适度大小的非负数，d（x）为正值有界扩散函数，非负常数k1，k2为控制扩散方向上的一组基，且k1+k2≠0，线性源项f（x，t）为定义在［a，b］×［0，T］上的已知函数，分数阶微分算子分别称为函数u（x，t）正规化R-L回火α（1＜α＜2）阶左侧和右侧导数，定义为方程（2）和（3），即：

定义1（左、右R-L回火分数阶导数）设1＜α＜2，函数u（x，t）定义在区间［a，b］×［0，T］上，Γ（·）为伽马函数，则称：

当λ=0时，左、右R-L回火分数阶导数退化成左、右R-L分数阶导数.

1 变系数回火分数阶扩散方程的基本结论

在文献［4］中，Li和Deng提出了一种具有二阶精度的回火加权移位Grünwald算子逼近正规化R-L回火的α阶（1＜α＜2）左侧和右侧导数的数值方法，并利用C-N方法逼近一阶时间偏导数，得到了在时间和空间上均具有二阶精度的常系数回火分数阶扩散方程的离散格式，并证明了该格式的稳定性和收敛性.笔者简要回顾回火加权移位Grünwald算子及相应的结论.

分别取两个正整数N和M，令空间步长为h=（b-a）/（N+1），时间步长为τ=T/M，则空间和时间的分割分别为xi=a+ih（i=0，1，…，N+1）和tm=mτ（τ=0，1，…，M）.由文献［4］得，方程（2）和（3）在网格点（xi，tm）处具有如下逼近格式：

其中，φ（λ）=（γ1ehλ+γ2+γ3e-hλ）（1-e-hλ）α.

序列｛｝k≥0满足关系式：

这里w0（α）=1，当k≥1时，方程（4）中的系数γi（i=1，2，3）满足方程（5）：

显然，在方程组（5）中，方程的未知量的个数多于方程的个数，因此，方程组（5）有无穷多解.通过直接计算，可得方程组（5）的3组解：

此外，序列｛gk（α）｝k≥0在方程组（5）解集的基础上，满足引理1的性质.

引理 1对于 1＜α＜2，λ≥0，如果γi（i=1，2，3）满足下列 3个条件之一：

2 数值离散格式

设｛u（xi，tm）∣0≤i≤N+1，0≤m≤M｝和｛∣0≤i≤N+1，0≤m≤M｝分别为回火分数阶扩散方程（1）的精确解和数值解.令利用 C-N 隐差分格式离散时间一阶偏导数、二阶中心差分离散空间一阶偏导数，以及Li和Deng提出的空间二阶回火加权移位Grünwald差分算子离散正规化R-L回火分数阶导数［4］，则对i=1，2，…，N和m=1，2，…，M-1，得到式（6）：

该差分格式是无条件稳定的，以及在空间和时间上的误差都满足2阶精度要求，详见文献［1］.记则式（6）的矩阵形式为：

其中，I为N阶单位矩阵，A=εk1G+εk2GT+η（k2-k1）W，D=diag（d1，d2，…，dN），ρm表示截断误差向量，并满足‖ρm‖∞=O（h2+τ2），W为三对角矩阵，G为Toeplitz矩阵，即：

关于数值离散格式（6）的收敛性证明在文献［1］中已经展开了讨论.然而，文献［1］中的证明是基于矩阵DA是负定矩阵这一条件的.事实上，当矩阵DA不是负定矩阵时，该离散格式在时间和空间上仍具有二阶精度收敛性，这一点也可以从文献［1］中例2的数值结果中看出.基于此，受文献［11］的启发，我们将方程（7）进行等价转换，并探讨收敛性在矩阵DA不加负定这一条件时成立的可能性，以下将就此展开讨论.

3 收敛性分析

在给出离散格式（6）的收敛性证明之前，先给出一些收敛性分析需要用到的定义及引理.

定义 2设向量v=［v1，v2，…，vN］T∈ℝN×1，h为空间步长，定义向量v的离散的L2范数定义为：‖v‖L2=向量v的2-范数定义为：.由定义2，可得，向量v的L2范数与2-范数之间的关系为

引理2令R（z）为在Rez≤0条件下的有界有理函数，对任一半负定矩阵A，则有：‖R（A）‖2≤成立［12］.

引理3［13］设矩阵A∈ℝn×n是正定（负定）矩阵，则vTAv＞0（＜0）对所有非零实向量v都成立，当且仅当它的对称部是正定（负定）的.

接下来，给出离散格式（6）的收敛性证明定理.

定理1设Dm是方程（1）的精确解向量，且um是差分格式（6）的解向量，当系数γi（i=1，2，3）满足引理1的假设之一，则：‖Um-um‖L2≤C（h2+τ2），对所有1≤m≤M都成立，其中，C是不依赖于m，τ和h的常数.

证令对j=1，2，…，N有则对0≤m≤M-1有：

由文献［4］可得，G为负定矩阵.又因为根据引理3可得，A为负定矩阵.进一步，也为负定矩阵.因此，为可逆矩阵，则方程（9）可化为：

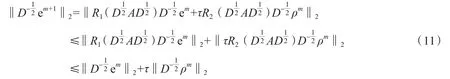
由定义2，向量的L2范数和2-范数之间的关系，在方程（11）两边同时乘以，得：

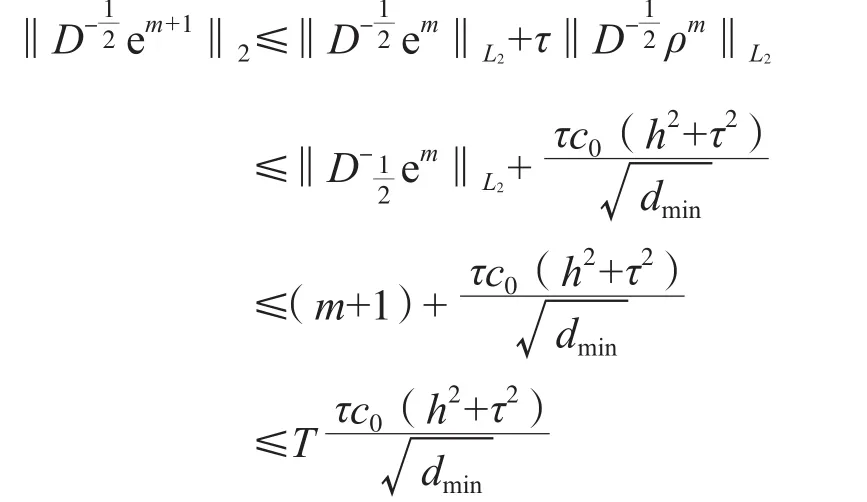
其中c0是一个正常数，更进一步，令um+1‖L2≤C（h2+τ2），即对 1≤m≤M，有：‖Um-um‖L2≤C（h2+τ2）.定理得证.

4 结语

讨论了利用C-N方法和回火加权移位Grünwald算子离散一类变系数回火分数阶扩散方程，得到了方程的数值离散格式，利用合同矩阵的性质，给出了数值格式收敛性的理论分析.该收敛性的证明和已有的研究成果相比，所需要的条件较弱，适用范围更广.