结合速度障碍法的无人艇编队控制策略研究
徐 杨,邵 兴
(1. 中国船舶集团有限公司第七一〇研究所,湖北 宜昌 443003;2. 清江创新中心,湖北 武汉 430076)
0 引言
随着国家对于海洋科学的不断重视和无人装备技术的进一步发展,水面无人艇作为一种新型的无人探测作业设备得到了快速的发展与广泛的运用。在民用方面,水面无人艇可用于内河航运、海洋环境检测、应急救援等领域;在军用领域,可用作区域侦察、中继通信、探雷探潜等用途。由于水面无人艇运动灵活性高且部署成本低,编队集群作业是水面无人艇的一类重要作业方式,编队控制技术也成为了水面无人艇当前研究的热点方向。当前,编队控制的主要方法有领航者-跟随者算法、虚拟结构法和基于行为的编队控制算法[1]。
领航者-跟随者算法作为一种结构简单、易于扩展的编队控制算法在实际工程实践中得到了广泛的运用。杨震等根据领导者的位置以及航向角信息来构建出一艘参考船,使其运行轨迹能够在固定时间内实现对参考船轨迹的跟踪,并利用反步法以及上下界滑模法设计一个鲁棒控制策略,使跟随船的实际轨迹能够跟随领航船的轨迹[2]。Cui基于领航者的位置信息和预设编队结构信息设计虚拟水下航行体,通过虚拟体产生期望轨迹和速度,并利用Lyapunov理论以及反演法设计控制律实现了跟随船对虚拟船的轨迹实时跟踪[3]。李良[4]等提出了一种基于改进跟随领航者法的编队控制方法,将对跟随者的航向和速度控制简化成单一的速度控制,并通过仿真实验和湖上试验进行了验证
相比于领航者-跟随者算法,虚拟结构法将编队描述为刚体运动,转化为时变的目标跟踪问题。适用于外界干扰少、运动模型确定的编队控制。潘无为等采用虚拟结构与人工势场相结合的编队控制算法,研究了存在障碍物条件下,多AUV系统的编队形成、编队保持和编队变换问题[5]。基于行为的编队控制算法通过定义编队成员的行为规则约束、协调编队动作,易于描述,但无法确定编队系统的整体行为,同时也无法用数学手段定量分析编队队形的稳定性。
基于行为的无人艇编队控制算法将无人艇的作业任务分解为多种行为(编队保持、进行避碰、目标跟踪等),并将各类行为分解为期望控制输出,通过行为融合模块控制无人艇运动。哈尔滨工程大学的姜大鹏[6]对基于行为的多AUV协调控制方法进行了研究,针对多AUV的编队控制问题设计了多种基本行为,采用基于多目标值优化的方法进行行为融合,并采用IvP计算模型对行为决策空间进行离散化处理以保证决策的实时性。基于行为的多无人艇编队控制基础结构简单,具有良好的实时性,可组成复杂的编队行为,但缺少相应的系统稳定性分析,不利于理论计算。
本文针对领航者-跟随者算法在编队形成过程中的缺陷,提出将速度障碍法引入领航者-跟随者算法,并在此基础上运用威胁评价函数协调编队运动,避免编队碰撞,提高编队控制的稳定性和安全性。
1 水面无人艇运动模型
为建立水面无人艇编队控制仿真平台,需建立水面无人艇的运动及动力学模型。结合水面无人艇的运动特性,本文只考虑无人艇水平面的运动模型,即只建立无人艇的纵荡、横荡以及艏摇3个自由度的数学模型,如图1所示。

图1 无人艇运动模型Fig.1 Motion model of unmanned surface vehicle
为简化模平面的三自由度数学模型,给出假设[7]:1)无人艇左右严格对称,即满足 Ixy=Iyz= 0 ;2)无人艇的质量均匀分布,且无人艇重心位于艇体坐标系原点;3)忽略无人艇在垂直面上的运动。
通过以上3个假设,可得出无人艇在水平面的三自由度数学模型:
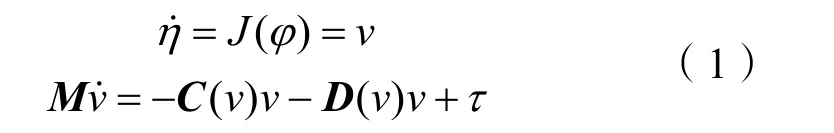
式中:η表示无人艇在大地坐标系下的位置信息,即纵向位置、横向位置和艏向角;v表示无人艇在大地坐标系下的速度信息,即纵向速度、横向速度和艏向角速度;τ表示无人艇控制力和力矩输入;M为惯性参数矩阵;C(v)为科氏力矩阵;D(v)为阻尼矩阵。
本文中所描述的水面无人艇为欠驱动水面无人艇,通过喷泵提供无人艇的前进推力,倒斗提供无人艇的转艏力矩,其基本控制器包括速度控制、艏向控制,路径跟踪、目标跟踪等控制算法的实现依赖于上述 2种基本控制器。水面无人艇通过舵、倒斗、喷泵为其提供前进推力和转艏力矩,并通过运动控制器实现速度控制、艏向控制、航迹跟踪等基本控制功能;激光雷达、光电摄像头和导航雷达为无人艇提供环境态势信息,并通过运动规划实现无人艇的目标跟踪、路径规划、动态避碰等功能。
2 编队控制基本策略模型
本文采用领航者-跟随者算法作为编队控制的基本结构。领航者采用路径跟踪控制的方式跟踪既定的航线路径,跟随者采用目标跟踪的方式跟踪虚拟目标点,虚拟目标点由领航者当前的位置和编队控制结构计算得出[8]。领航者和跟随者通过各自控制算法计算得出其期望速度和期望艏向,通过艏向和速度控制器实现编队控制[9]。
2.1 领航者路径跟踪算法设计
在实际工程运用中,水面艇的路径跟踪分为直线跟踪和圆轨迹跟踪2种形式。本文构建目标航向渐进函数,可计算得出目标区域内任意一点对于目标路径的趋近航向[10]。
设当前无人艇的所在位置与目标路径的最短距离为D。
1)当目标路径为直线段时,最短距离D为无人艇与目标直线的侧向距离,目标航向lδ为目标路径的方向角。最短距离D计算公式为

式中:目标航向可表述为 A x+By+C= 0 ;(x, y)为无人艇的所在位置。当无人艇位于目标路径左侧时,距离为负;位于目标路径右侧时,距离为正。
2)当目标路径为圆弧段时,最短距离D为距离无人艇位置的最近圆弧切线和无人艇当前位置的距离,目标航向lδ为距离无人艇位置的最近圆弧切线的方向。最短距离D计算公式为
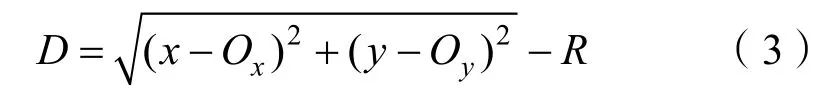
式中:(x, y)为无人艇的所在位置;(Ox, Oy)为目标路径的圆心;R为目标路径的半径。当无人艇位于目标路径外侧时,距离为负;位于目标路径内侧时,距离为正。

图2 直线跟踪路径导引Fig.2 Line tracking path guidance

图3 圆弧跟踪路径导引Fig.3 Circle tracking path guidance
无人艇所在位置期望航向角dψ与目标航向lδ之间的偏差航向ψΔ可通过式(4)计算。

式中ψmax为最大偏差航向角。对于函数 f( D)来说,应该满足特征:①函数有界,且取值范围为(-1,1);②函数连续可导,且在D的取值范围内为严格单调递增的奇函数。
本文选取S面函数为函数f( D)。
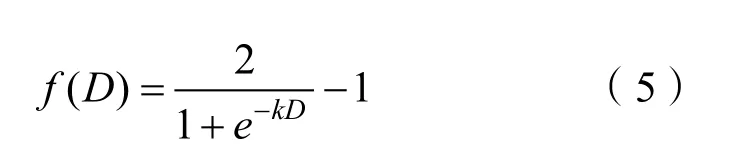
式中,k为航向变化参数,代表偏差航向的变化速率。其值越大,偏差航向的变化速度越大。
无人艇期望航向角dψ可计算得出:
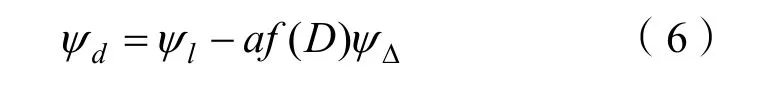
式中a为符号函数。当目标路径为直线段时,常值为正;当目标路径为圆弧段时,若圆弧段的绕行方向为顺时针,则a常值为正,若圆弧段的绕行方向为逆时针,则a常值为负。
上文所构建的目标航向渐进函数为外环控制器,计算得出目标航向,目标航向作为无人艇航向控制器的输入控制无人艇的舵/斗渐进跟踪目标路径。
2.2 跟随者目标跟踪算法设计
本文采用目标跟踪的方式实时跟踪编队队形,建立目标坐标系计算跟随者的跟踪误差。如图4所示,目标坐标系将坐标原点Od建立在领航者位置处,坐标轴OXd沿领航者艏向方向,坐标轴OYd为坐标轴OXd顺时针旋转90°所得。
无人艇的跟踪误差可由式(7)得出:

式中:s为无人艇的纵向跟踪距离;e为无人艇的横向跟踪距离; Rn(θ)为从大地坐标系到目标坐标系的旋转矩阵;qf为跟随者在大地坐标系下的位置;ql为领航者在大地坐标系下的实际位置。
无人艇的横向跟踪距离可通过调整无人艇的艏向角进行调整。根据横向距离误差(e -ed),可计算无人艇的期望艏向角ψd:

式中:lθ为领航者的艏向角;Δe为前视距离;一般为艇长的2~3倍。
无人艇的纵向跟踪距离可通过调整无人艇的航速进行调整。根据纵向距离误差(s -sd),可计算无人艇的期望速度vd:
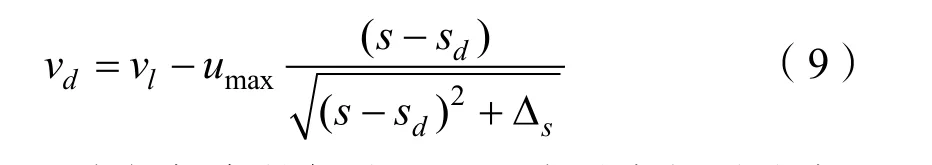
式中:vl为领航者的航速;umax为最大相对速度;Δs为相对速度调整项。
3 基于威胁评价的编队控制避碰策略
经典的领航者-跟随者算法在实际运用中有以下不足[11]:1)过度依赖编队领航者;2)无法灵活进行编队变换;3)存在编队形成过程中的避碰风险。
为了降低编队形成过程中各编队成员相互碰撞的风险,本文引入速度障碍法作为编队控制过程中的避碰策略。在常规的水面无人艇的避碰中,由于无人艇所携带的传感器难以精确地获取障碍物的速度位置信息,将速度障碍法运用于无人艇避碰时往往需要实时对障碍物的运动信息进行滤波和预测后,得到相对准确的障碍物运动信息才能发挥出良好的避碰性能。而在编队控制中,由于编队各成员的运动信息实时已知,速度障碍法可实时准确地计算出避碰角度。
3.1 基于椭圆的速度障碍法
由于无人艇的物理外形特征,本文采用文献[12]中的基于椭圆的速度障碍法计算无人艇的可行避碰角度。在椭圆速度障碍法中:P和V分别表示无人艇在水平面的位置和速度矢量;A和B分别表示无人艇椭圆和障碍物椭圆,两者的半长轴分别沿着其速度矢量方向;VA表示无人艇的速度矢量;VB表示障碍物的速度矢量;VBA表示无人艇相对障碍物的速度矢量,可通过下式求得。


图5 基于椭圆的速度障碍法示意图Fig.5 Schematic diagram of ellipse-based velocity obstacle algorithm
假设无人艇和障碍物的运动状态保持不变,当相对速度VBA的方向与障碍物B相交时,即可认为无人艇和障碍物在将来某一时刻t会发生碰撞。定义使得A和B碰撞的相对速度VBA的集合为RCCAB,称之为相对碰撞区域。为方便在多个障碍物环境下得统一描述,将每个障碍物的RCC定义在无人艇的绝对速度空间,称之为速度障碍VOAB。
当存在多个障碍物时,总的速度障碍VO为各障碍物VO的并集:

3.2 基于威胁评价的编队避碰算法
通过速度障碍法计算出速度障碍VO后,非VO集合中的矢量方向即为无人艇可选的避碰艏向。考虑到无人艇的转弯性能,一般选取无人艇当前编队期望艏向角aψ附近的艏向区间作为避碰艏向选择。即:
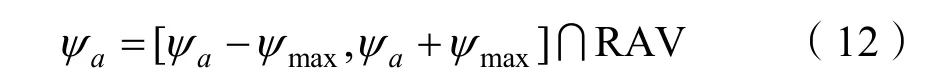
式中:aψ为由式(8)计算所得的期望艏向角;ψmax为最大允许转弯角度;RAV为可行避碰区间。
在编队成员间使用速度障碍法进行避碰需要对避碰编队成员间的避碰艏向进行协调。本文采用编队成员i所受势场力的矢量和作为编队成员i的威胁评价,并以编队成员i的威胁评价计算编队成员i的期望转艏角度。

式中:Frep为编队成员i所受的排斥力(当编队成员i具有碰撞威胁且与具有碰撞威胁编队成员处于距离R内时不为0);arep为斥力系数;dis为编队成员i与其他编队成员的相互距离,通过求解编队成员i的总斥力Ftrep可计算编队成员i的碰撞威胁。
f( x)为编队成员i的威胁评价函数[13],通过排斥力Frep的矢量和计算编队成员i所受的碰撞威胁程度。当编队成员之间的相互距离越近,编队成员i的威胁程度越高,其转艏角度也就越大,当存在多个碰撞威胁时,按照Frep的矢量和计算编队成员i的碰撞威胁程度。
编队成员的期望艏向角:

式中α为符号函数。当Ftrep的矢量方向沿速度矢量p左侧时,α取负;当Ftrep的矢量方向沿速度矢量p右侧时,α取正。
当无人艇按照既定队形进行编队时,领航者-跟随者算法作为编队控制的基本策略导引无人艇进行编队航行,当跟随者附近出现障碍物时,由威胁评价函数判断跟随者是否有碰撞风险。若具有碰撞风险,则由速度障碍法计算器避碰艏向,跟随者按避碰艏向规避障碍物。
4 仿真试验
4.1 领航者-跟随者编队控制试验
图6为同一仿真试验条件下的一字型编队队形下3艘无人艇的编队控制效果,该试验假设3艘无人艇位于同一出发点同时出发,最终在100个仿真步长下形成了稳定的编队队形。
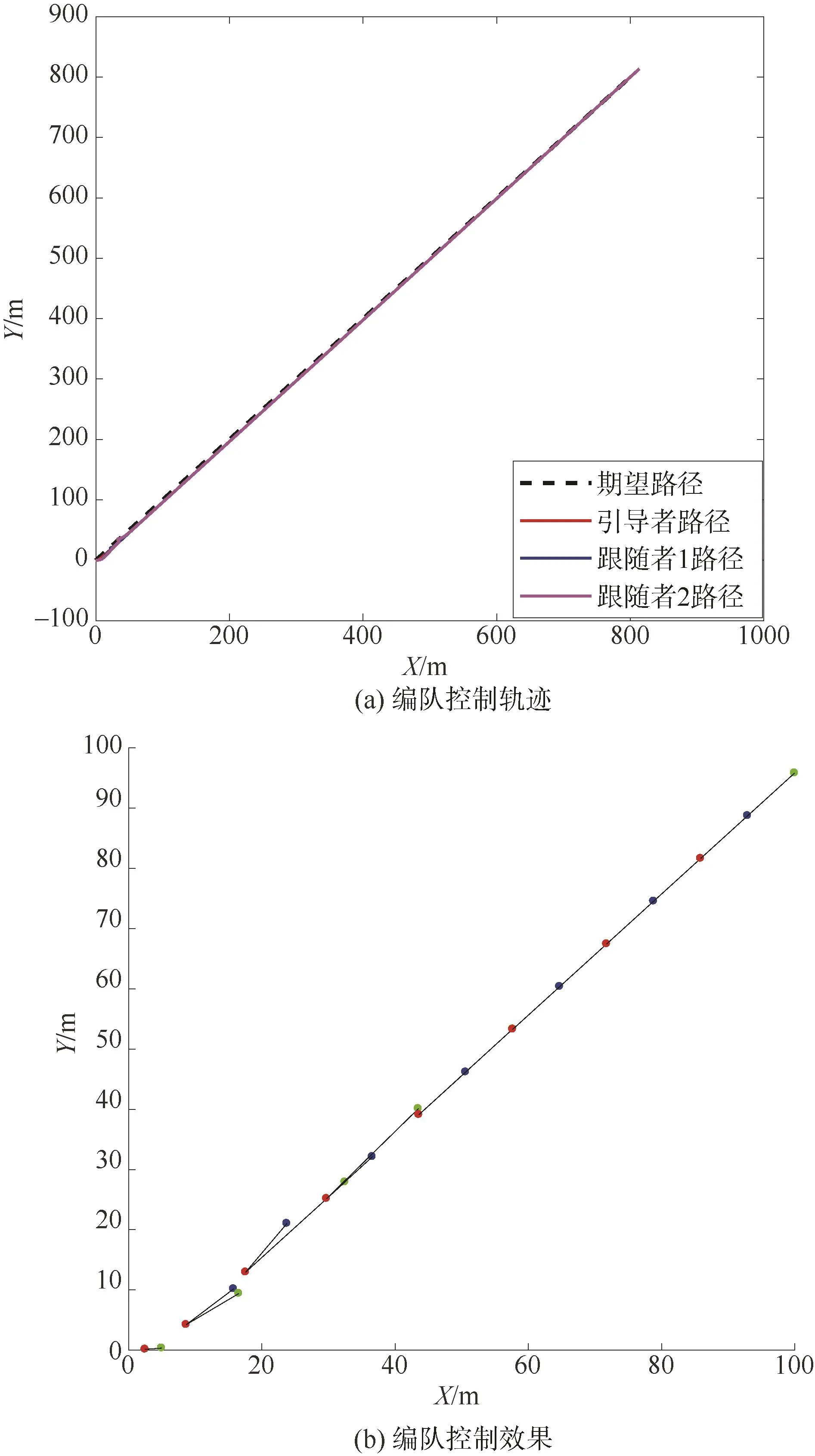
图6 一字形结构下的编队控制效果Fig.6 Formation control effects under linear shape structure
仿真结果表明,领航者-跟随者算法能够有效地对指定编队队形进行组织和跟踪。
4.2 编队避碰算法仿真试验
图7为编队控制时2个编队成员的初始状态,p和q分别表示在该编队成员的艏向角。在该种状态下编队成员具有相互碰撞的风险,本文对该类初始状态下的编队控制效果进行对比仿真试验。图8为带有避碰策略下的编队形成过程。
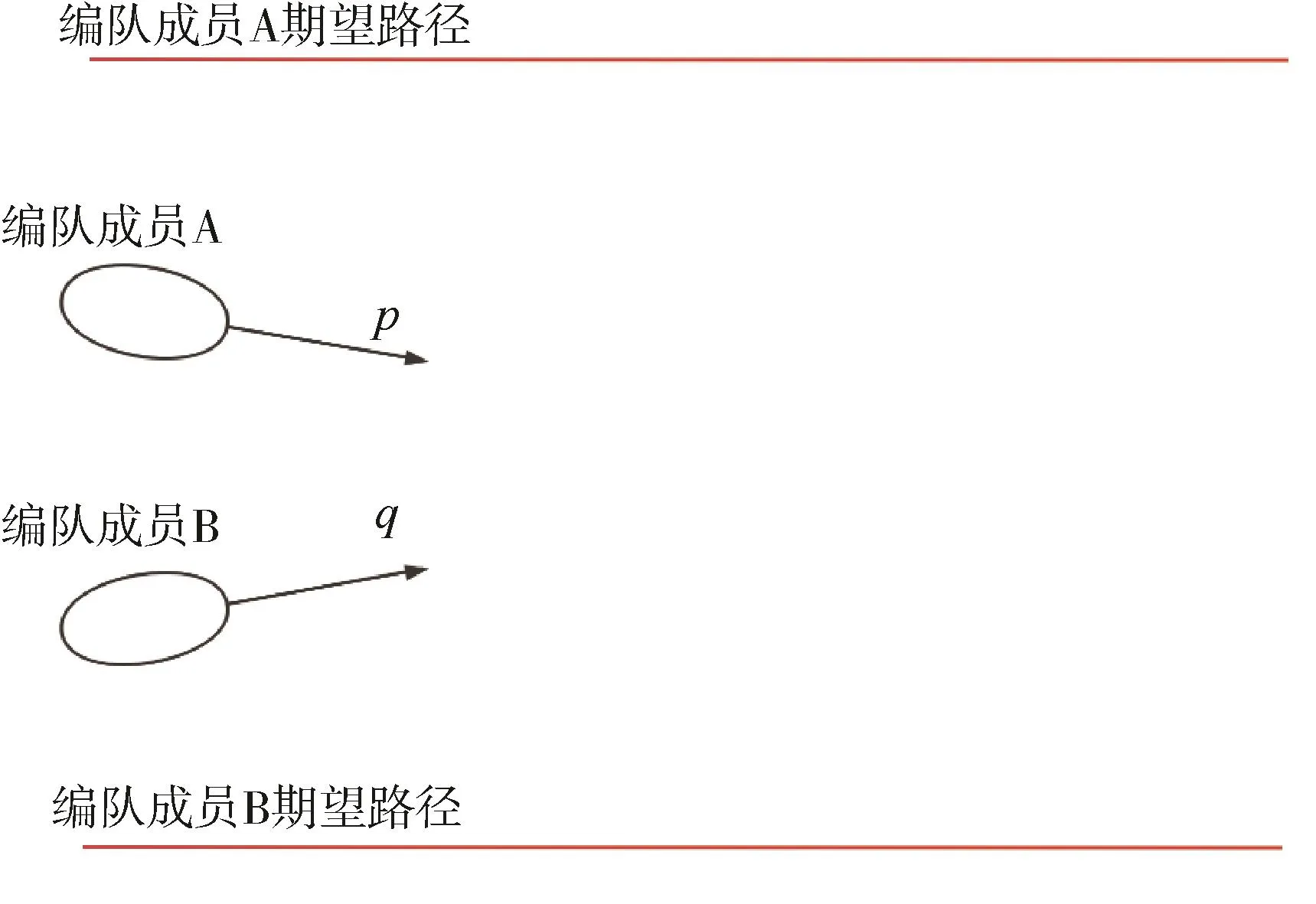
图7 编队成员初始状态Fig.7 Initial status of formation member
图 8(a)中,带有避碰策略的编队控制算法可在50 m之内初步形成有效的编队队形,而图8(b)中,则需要115 m的距离形成有效的编队队形。相比于无避碰策略的编队控制算法,带有避碰策略的编队控制算法编队形成速度加快,且避免了原本可能发生的碰撞编队成员碰撞风险。

图8 有无避碰策略的编队形成过程对比Fig.8 Comparison of formation with and without collision avoidance strategy
5 结束语
本文通过领航者-跟随者算法成功解决了多无人艇编队控制问题,且分析了领航者-跟随者算法的缺陷。通过将速度障碍法引入到编队控制中,解决了领航者-跟随者算法在编队形成过程中的编队碰撞问题。仿真试验表明:该编队控制避碰策略显著改善了编队形成过程中的相互碰撞问题,使领航者-跟随者算法更适合实际工程试验中的编队控制问题,为后续的湖上试验创造了有利的条件。

