基于模糊数学的AIS和被动声呐航迹关联算法研究

孙 峰，邱家兴，宋 彦

（1. 海军潜艇学院，山东 青岛 266000；2. 自然资源部北海预报中心，山东 青岛 266000）

0 引言

在复杂多目标应用背景下，被动声呐信息获取能力先天不足，存在信噪比低、识别误差大等问题，即便是通过后期复盘分析、人工听信识别，也很难单独依靠被动声呐信号获取足够的目标信息。而安装在民用船只上的船舶自动识别系统（Automatic Identification System，以下简称 AIS系统）采取卫星导航确定目标位置，准确度高、实时性好。因此，将AIS数据与被动声呐信号进行轨迹关联和信息融合，可以有效提高被动声呐目标识别准确度。

目前，国内外关于航迹关联、信息融合的研究主要采用的算法有加权法[1]、遗传算法[2]、独立序贯法[3]、最近邻域法[4]等。这些方法大多基于雷达、激光等高精度传感器数据，环境干扰小、信噪比高，识别结果相对精确。但相同方法应用于被动声呐信号这种高误差、低信噪比的数据上时，效果并不理想。另外，AIS系统基于VHF实现数据传递，当网络堵塞或船舶远离海岸时，数据掉帧、跳帧、出现奇异点的情况比较普遍，也不利于数据融合。因此，本文主要对AIS数据进行预处理，并在此基础上，应用模糊数学的方法对两者航迹进行关联，实现从硬判定到带有可信度因子的软判定，进一步提高关联结果的鲁棒性、适用性和准确度。

1 AIS系统和被动声呐数据特点

1.1 AIS系统数据特点

AIS系统发送的报文包含了船速、位置等动态信息和船名、呼号等静态信息。由于AIS系统采用卫星导航系统定位，精度一般在30 m以内，数据点的位置误差基本可以忽略不计。但在实际应用中，受VHF通信链路不稳定等因素影响，AIS系统存在报文频率不稳定或者数据错误的情况。

1.2 被动声呐系统数据特点

被动声呐仅能测得目标方位信息，无法获知目标距离。在测量精度上，不同阵型的被动声呐有所差异，但误差普遍在1.5°～10°之间，线列阵声呐还存在左右舷模糊问题。如遇到复杂水声环境、观测盲区，误差也可能接近或超过15°。以美国的AN/SQR-19型被动拖曳线列阵声呐为例，其正横方向测向精度小于2°，被动探测距离可达 70 n mile[5]。而按照目标距离30 n mile、GPS定位误差100 m计算，AIS系统测向精度为0.1°。由此看，被动声呐数据在目标测量精度和获取信息丰度等方面差距明显。

2 基于模糊函数的AIS和被动声呐航迹关联算法

模糊数学是研究和处理模糊性现象的一种数学理论[6]，对于解决 AIS系统和被动声呐间的航迹关联问题具有较好的适应性。因此，本文采用模糊函数关联算法对被动声呐与AIS系统航迹进行关联。具体算法流程如下。

2.1 区域划分

为减小航迹关联计算量，在关联判定前先进行区域划分，筛选出在被动声呐探测范围的AIS数据。若被动声呐数据工作时间段为t1～tn-1，声呐装置位置为（lon0，lat0）...（lonn-1，latn-1），则 AIS 数据的时空筛选范围分别如下。

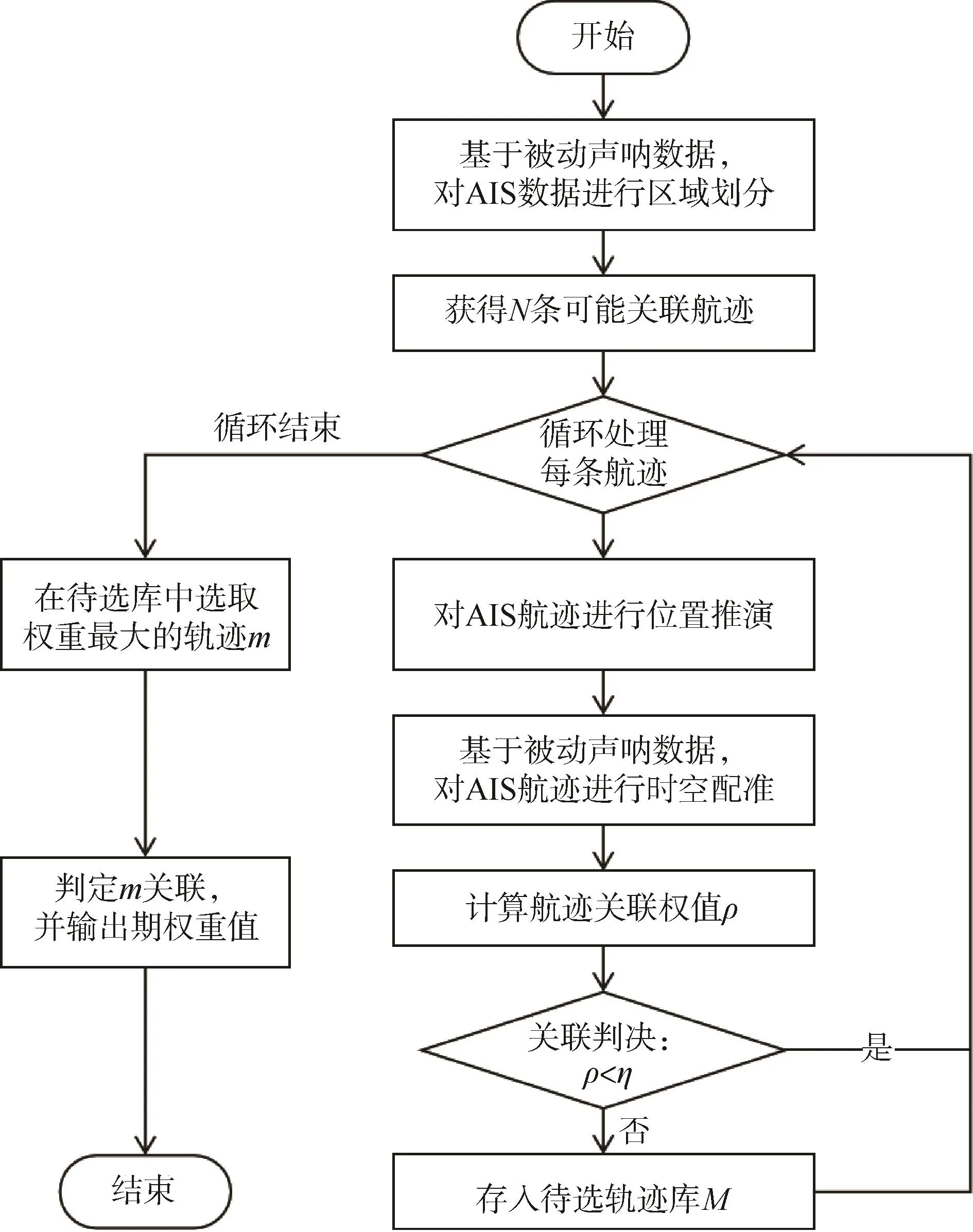
图1 基于模糊函数的AIS和被动声呐航迹关联算法流程图Fig.1 Flow chart of the track correlation algorithm for AIS and passive sonar based on fuzzy function

式中：Δt为声呐数据时间段向外延拓宽度，通常设为1 800 s；R为被动声呐最大探测距离，根据不同型号声呐性能而定；Δlon和Δlat是最大探测距离R经过换算后对应的经纬范围。

2.2 航迹推演

AIS报文频率不固定，大部分时刻的船舶位置信息需要推演获得。设某船舶AIS航迹数据为{（t0，lon0，lat0，v0，φ0）...（tn-1，lonn-1，latn-1，vn-1，φn-1）}，其中loni和lati分别为船舶在ti时刻所处经纬度，vi、φi为 ti时刻船舶航速和航向。由于船舶正常航行时短时间内航速和航向都比较稳定，可以简化为匀速直线运动[7]，据此可推演得到任意时刻的船舶位置。另外，由于航迹推演有一定的不可靠性，因此引入位置概率 pi，代表求得航迹位置的可靠程度，其取值范围为（0，1），pi越接近1意味着航迹位置越可靠。假设欲求tj时刻船舶轨迹，具体算法如下。

1）若tj＜t0，则理解为船舶以v0的速度沿φ0方向由 tj时刻行驶至 t0时刻。考虑船速与经纬度间的变换关系，可以推导得tj时刻船舶经纬度分别为

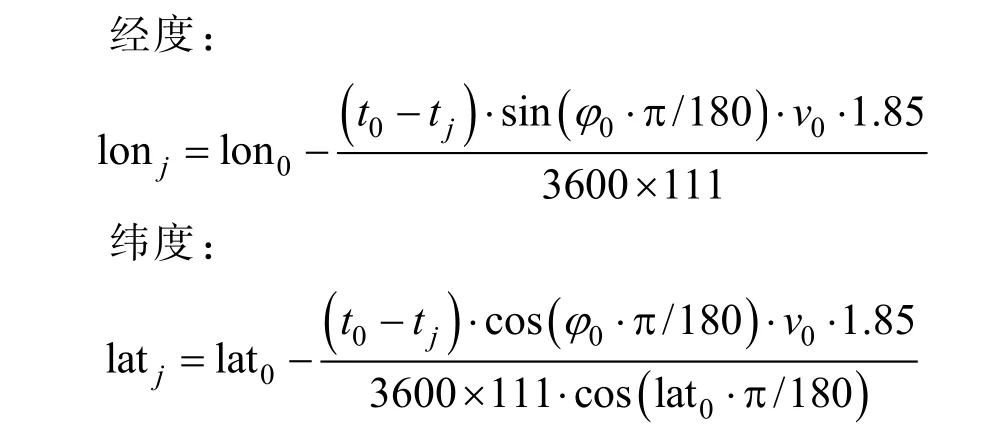
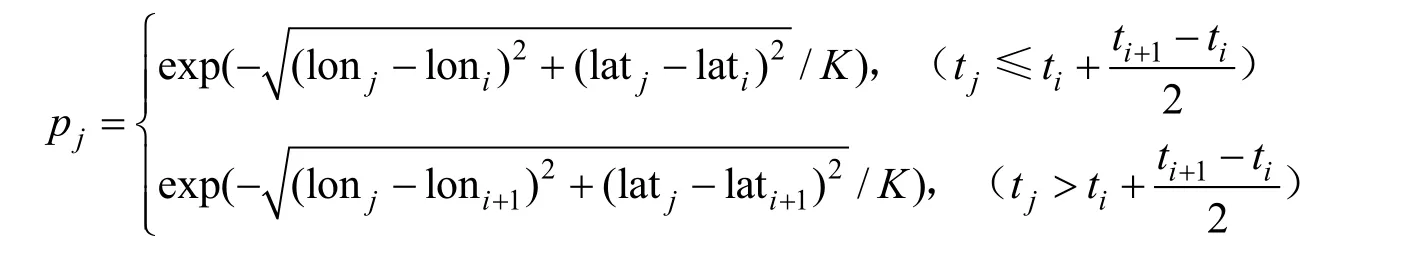
3）若tj＞tn-1，则理解为船舶以vn-1的速度沿vn-1方向由tn-1时刻行驶至tj时刻。考虑船速与经纬度间的变换关系，可以推导得Tj时刻船舶经纬度分别为

2.3 时空配准

AIS与被动声呐数据的时空坐标不匹配，需要统一时空坐标系。空间坐标方面，考虑到被动声呐数据信息丰度弱、测量精度低，空间信息不易转化为其他坐标格式，故将AIS位置坐标统一到以声呐装置船艏方向为零点的相对角度坐标系中，转换公式为

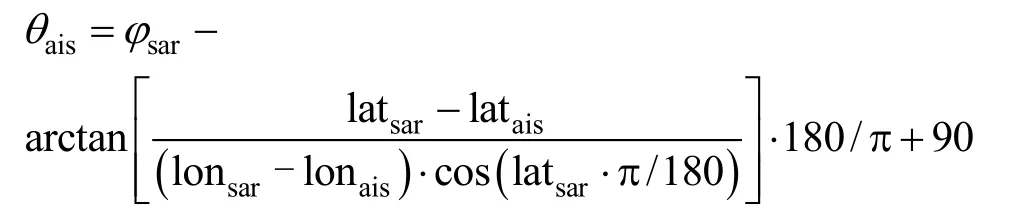
时间坐标方面，从方便计算的角度考虑，应统一到 Unix格式的绝对时间坐标上来[8]。即tsar′=

2.4 关联判决

航迹关联本质上是一个二元判决问题。对于被动声呐航迹Si与AIS系统任意航迹Aj，总存在关联、不关联 2种可能。考虑到影响航迹关联的因素主要有角度、距离和位置可靠性等 3个，根据模糊数学原理，分别设计 3个因素对应的隶属度函数，并基于隶属度函数得出关联概率。设被动声呐航迹，其中θsk为tk时刻目标角度；AIS航迹，其中θsk、rsk、psk分别代表tk时刻船舶相对声呐的角度、距离和其位置可靠性。则关联概率表达式为

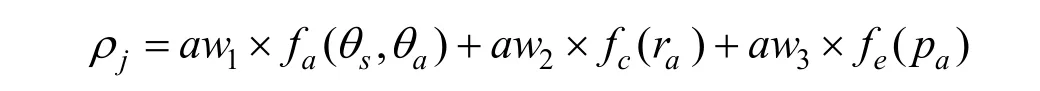
关联概率 ρj越大，代表航迹 Si与 Aj的关联程度越高。若航迹 Aj与 Si均不关联，计算过程中有可能将ρj中的相对最大者判定为关联航迹，但这是与实际不符的。因此，设立门限值η，使得其中μ为阶跃函数。即当ρi＜η时，判定航迹不关联，η的取值根据被动声呐系统参数而定。

3 实验验证及其讨论

本文利用某型被动声呐在2019年12月16日6：53-7：23在东海某海域测得的数据与 AIS系统数据进行关联，以验证算法的有效性。

3.1 数据预处理

根据前文所述，首先对AIS系统数据进行区域划分和航迹推演，并将AIS系统数据和被动声呐数据进行时空配准。去除仅有1个AIS数据点的无效轨迹，被动声呐有效探测范围（100 km）内共有船舶轨迹141条。分别计算每条轨迹的位置 loci、相对距离 ri和相对声呐角度θi，所得结果如图2、图3所示。

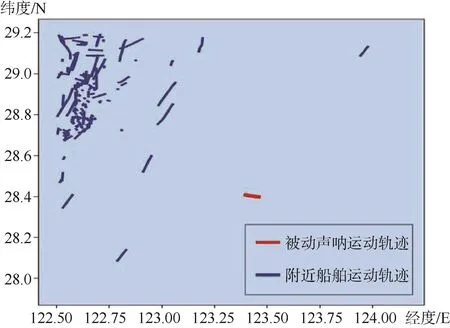
图 2 声呐和船舶运动轨迹图Fig.2 Motion tracks of sonars and ships

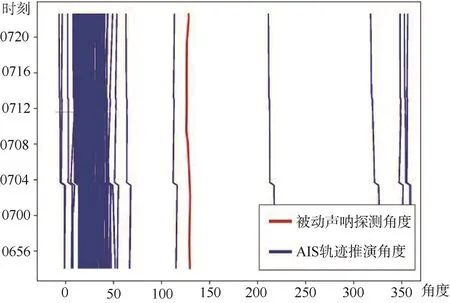
图3 船舶相对声呐角度变化Fig.3 Angle changes of ships relative to the sonars

3.2 设定权值参量

在计算关联概率前，应确定角度、距离和目标位置可靠性这3个因素对轨迹关联的影响程度，即设置超参数aw1、aw2、aw3的值。根据模糊函数关联算法原理，隶属度函数值分布越离散，对关联判决越有利，其对应的超参数所占权重就越高。因此，对预处理后的141条轨迹分别计算角度、距离和位置可靠性的隶属度函数值fai、fbi、fci，观察其分布情况。

可以明显看出，fa分布相对离散，特别是红色点与其他值差异明显，是最可能关联的航迹；fb的分布虽不如fa离散，但相对fc更好一些。因此在超参数设置时，应当有aw1＞aw2＞aw3。此设置方式与“角度差异是影响关联判决的主要因素”这一客观事实是相符合的。根据上述理论，结合经验，设置 aw1=0.6，aw2=0.25，aw3=0.15。

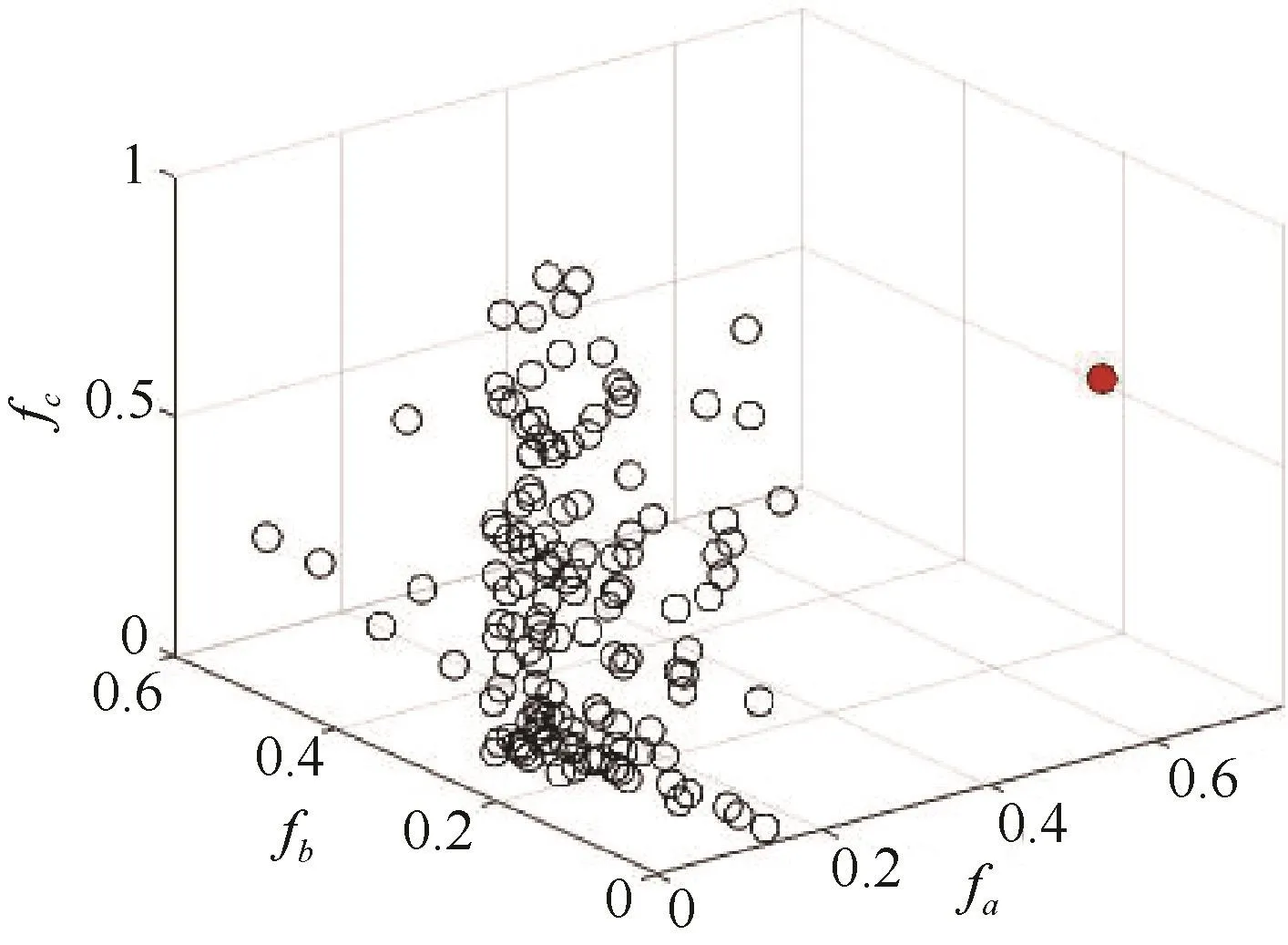
图4 隶属度函数fa、fb、fc分布Fig.4 Distribution of membership functions fa，fb，fc

图5 隶属度函数分布的fa-fb截面图Fig.5 Section view of membership functions fa-fb

图6 隶属度函数分布的fb-fc截面图Fig.6 Section view of membership functions fb-fc

另外，阈值η应参照被动声呐系统性能进行设定。假设声呐最大探测距离为120 km，最大测向误差为15°，按照关联概率计算公式，可求得η=0.561 2。考虑到AIS数据还存在误差，因此实际阈值应再小一些。

3.3 进行关联判决

表1 处理结果Table 1 Calculation results

根据以上数据，可判定船舶AMI的航迹与被动声呐航迹关联，关联概率为0.650 7；其余AIS航迹的关联概率均远小于阈值η，不具备关联的可能性。

4 结束语

本文分析了AIS系统数据和被动声呐数据的各自特点，提出了基于模糊数学的航迹关联判决算法，并对其进行了实验验证。从实验结果可以看到，该算法在航迹关联判决中取得了较好的效果。但此算法在判决过程中仅考虑了角度、距离和AIS位置可靠性等3个方面因素，其他诸如声呐测量经度、船舶运行状态等可能影响航迹判决的信息并未纳入考虑范围内。如何对这些因素进行建模分析，将是下一步的研究方向。