高雷诺数条件非线性弹簧下PTC圆柱流致振动数值模拟

樊天慧，周诗博，孙海，陈超核*

1 华南理工大学 土木与交通学院，广东 广州 510641

2 哈尔滨工程大学 航天与建筑工程学院，黑龙江 哈尔滨 150001

3 密歇根大学安娜堡分校 海洋可再生能源实验室，美国密歇根州 安娜堡 48109-2145

0 引 言

当一定流速的流体流过钝体时，流体会在钝体的两侧形成交替脱落的旋涡，若钝体在横向和流向上受到弹性约束，则旋涡作用在钝体上的流体力会使钝体发生振动，这种现象就是流致振动（flow-induced vibration，FIV）[1]。钝体的流致振动现象会对钝体的结构安全造成严重危害；不过，若利用得当，也可以使海洋流成为一种安全、清洁、高效的能源。因此，流致振动现象在许多领域都是研究热点，如海洋平台、桥梁结构、高层建筑，可再生能源等领域[2-5]。

最为常见的流致振动现象是涡激振动（vortexinduced vibration，VIV），其振动响应有自限性。Feng[6]在空气介质中进行了光滑圆柱横向振动实验，发现光滑圆柱的涡激振动存在初始分支和下部分支2 个分支，并且圆柱在一定的雷诺数范围内出现锁定状态。Williamson 等[7]对低质量比的圆柱涡激振动进行了大量实验研究，发现低质量比圆柱的横向振幅曲线会出现初始分支、上端分支和下端分支，并指出了各个分支所对应的涡脱模式，有2S 和2P 模式，S 表示单个旋涡脱落，P 表示一对旋转方向相反的旋涡脱落。Bearman[8]从雷诺数、振动方式、自由度和柱体数量等方面对涡激振动研究成果进行了综述。另一种常见的流致振动现象是驰振（Galloping），有着低频率、高振幅的失稳特性，振动响应随着流速的增加不断增强直至结构破损，比涡激振动更具有破坏性[9]。驰振的产生通常跟柱体的截面形状有关，对于光滑圆柱一般发生涡激振动而不会发生驰振，可以通过在圆柱表面或周围增加附属物的方式使之发生驰振，这种通过改变柱体表面结构控制振动响应的方法称为被动湍流控制（passive turbulence control，PTC）。Nakamura 等[10]通过实验发现无论柱体截面形状是否光滑，只要在柱体尾部增加一段长分隔板，都可以使柱体发生驰振。Park 等[11]通过在光滑圆柱表面上添加粗糙带的形式进行了流致振动物理模型实验，发现PTC 圆柱发生了驰振，振幅达到2.9 倍的圆柱直径，并且还可以在更大的流速范围内发生振动响应，从而提高了流致振动的能量转换效率。Sun 等[12]研究了质量比、阻尼比和刚度对PTC 圆柱流致振动能量转换效率的影响，发现能量转换效率随着质量比和阻尼比的增大而增大，而使圆柱发生起始振动的流速随着弹簧刚度的增大而增大。Wu 等[13]使用OpenFOAM 开源软件结合Spalart-Allmaras 湍流模型对PTC 圆柱进行了二维数值模拟，并与实验结果进行对比；结果表明模拟的振幅比曲线捕捉到了初始分支、上部分支和驰振分支，与实验结果相同。Zhang 等[14]采用FLUENT 软件模拟了不对称PTC 圆柱的流致振动，也成功得到4 个振动分支，并发现带有粗糙带一侧的振幅值偏小。

多数学者所研究的流致振动模型主要是将其简化为线性弹簧的质量−弹簧−阻尼线性系统，而非线性弹簧下的流致振动响应和线性弹簧下相比有所不同，主要表现在振幅响应、频率响应和锁定区间等方面。Gammaitoni 等[15]证明了合适的非线性模型装置可以有效提高能量产生效率。Mackowski 等[16]通过实验证明，和线性弹簧相比，非线性弹簧可以改变结构的固有频率，扩大VIV的锁定区间。Huynh 等[17]对非线性弹簧下的涡激振动进行了实验和数值模拟研究，得到的数值模拟的结果和实验值吻合得很好。Sun 等[18]和Ma等[19]在2 400≤Re≤12 000 高雷诺数下进行了分段弹簧支撑的PTC 圆柱流致振动实验，发现分段弹簧的回复力可以提高实验装置的能量转换效率。同时，Ma 等[20]通过实验研究了分段弹簧对串联双圆柱的影响，发现使圆柱初始振动的流速比单个圆柱要高。Li 等[21]进行了高雷诺数下三次方弹簧支撑的光滑圆柱涡激振动模型实验研究，发现三次方弹簧可以有效地扩大涡激振动的上部分支。Wang 等[22]应用重叠网格技术对低雷诺数下硬化弹簧刚度的光滑圆柱涡激振动进行了二维数值模拟研究，发现硬化弹簧的非线性越大，圆柱的振动响应就需要在更高的雷诺数范围内才能发生。Lyu 等[23]从柱体形状、被动控制方法、非线性弹簧、阻尼和多柱体等方面对非线性流致振动的文献作了全面综述。

综上所述，非线性弹簧下圆柱流致振动的响应特性与线性弹簧的差异显著，非线性弹簧下圆柱流致振动具有更加复杂的振幅特性、频率特性和流固耦合机理。本文针对高雷诺数下分段弹簧支撑的PTC 圆柱，将其简化为二维模型，在采用Spalart-Allmaras 湍流模型求解非稳态雷诺平均Navier-Stokes 方程组的基础上，通过计算流体力学软件FLUENT 对分段弹簧支撑下的PTC 圆柱流致振动进行数值模拟，并将其与实验结果进行比较，探讨分段弹簧对PTC 圆柱流致振动响应的影响，为提高能量转换装置的效率提供理论与技术支撑。

1 研究对象

文献[18]展示了美国密歇根大学海洋可再生能源实验室研究团队完成的一个物理实验，本文数值模拟采用了该文献的物理模型参数。实验中圆柱的实际长度L=0.895 m，直径D=0.088 9 m，长径比L/D=10.067。将该圆柱流致振动实验装置简化为二维单自由度的质量−弹簧−阻尼振动系统，即不考虑圆柱的三维展向效应，只考虑垂直于来流方向上的运动。

PTC 圆柱流致振动物理模型示意图如图1所示，U为来流方向上的均匀流速，阻尼ctotal=23.41 N·s/m，质量mosc=7.286 kg，排水质量md=5.425 kg，质量比m∗=mosc/md=1.343，圆柱表面上布置的对称粗糙带（PTC）是为了增大圆柱流致振动的响应，总厚度为0.847 mm，覆盖在圆柱表面的宽度为16°，粗糙带前边缘位置与圆柱前驻点相对圆心的夹角为20°。非线性弹簧刚度采用分段线性函数的形式，示意图如图2 所示。图2中Frestoring为非线性弹簧的回复力，y为圆柱振动的位移，K1和K2分别为第1 段和第2 段弹簧的刚度，K1=1 000 N/m，K2=200 N/m，y0为Frestoring(y)的分段点，取0.5D和1.0D。当圆柱位移|y|≤y0时，回复力仅由刚度为K1的弹簧决定，此时圆柱振动和线性弹簧一致；当|y|>y0时，两段刚度分别为K1和K2的线性弹簧共同构成回复力。

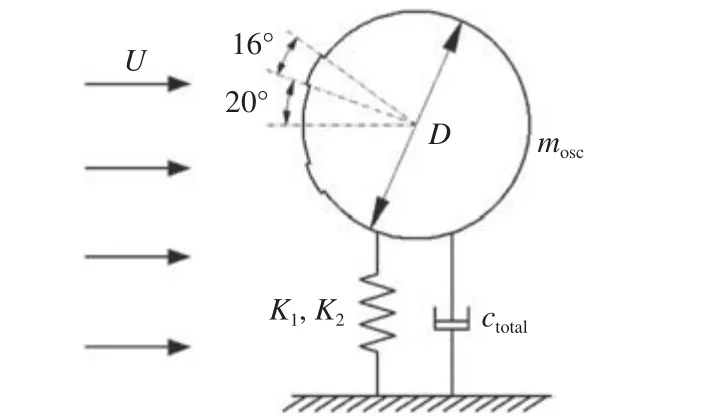
图 1 PTC 圆柱流致振动模型示意图Fig. 1 Schematic diagram of vibrating model of PTC-cylinder

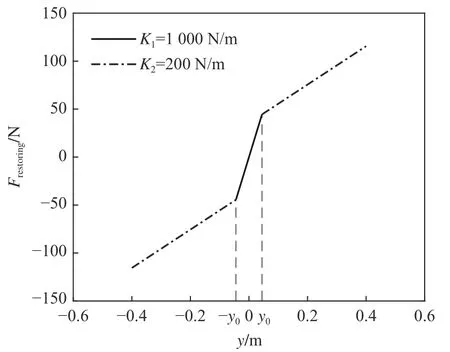
图2 非线性弹簧刚度函数Fig. 2 Nonlinear spring-stiffness function

2 数值计算方法

本文将物理模型简化为二维单自由度质量−弹簧−阻尼系统，利用计算流体力学方法，选取Spalart-Allmaras 湍流模型求解Navier-Stokes 方程组，在用户自定义函数(UDF) 中求解振动方程，实现对分段弹簧下的PTC 圆柱流致振动的数值模拟。

2.1 流体控制方程

对于不可压缩黏性流体流动，本文用二维非稳态的雷诺平均Navier-Stokes (RANS)方程组结合一方程Spalart-Allmaras 湍流模型[24]进行数值模拟。其连续性方程和动量方程在笛卡尔坐标系下的守恒形式为：

2.2 柱体运动方程

二维单自由度圆柱非线性流致振动的动力学特性可以由质量−弹簧−阻尼模型描述，模型中弹簧的回复力由两段刚度不同的线性弹簧组合产生，其运动方程和弹簧回复力表达式为：

本文采用有限体积法对流场离散化求解。首先，在每个时间步内，由FLUENT 软件求解RANS方程组，获得流场对圆柱的升力；然后，在用户自定义函数（UDF）中通过四阶龙格−库塔法求解运动方程，得到圆柱的运动速度和位移；最后，再将速度和位移输入FLUENT 进行下一个时间步的迭代计算，实现流固耦合作用的计算模拟。动量方程和连续性方程的压力速度耦合采用SIMPLEC算法求解，对流项和压力项采用二阶迎风格式，扩散项为中心差分格式。

2.3 计算模型

本文采用的计算模型如图3 所示。整个流场计算区域为14D×30D尺寸的矩形区域，圆柱中心距离流场入口边界处10D，距离出口边界处20D，距离上、下边界7D。在圆柱周围设置2D×2D的正方形运动区域，运动区域内的网格不发生变化，在横向上随圆柱同步做上下振动。为了避免网格负体积的产生，使计算结果更加准确，动网格采用动态铺层法。

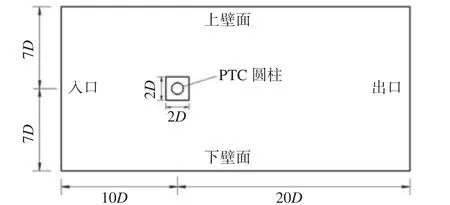
图3 计算模型Fig. 3 Computational model

边界条件设置：入口处采用速度入口边界条件(velocity inlet)，来流方向速度u为均匀来流速度U，横向速度v为0，即u=U,v=0；出口处采用自由出流边界条件(Outflow)，即=0；上、下壁面取固定壁面边界条件(Wall)，法向速度和切向速度都为0，即u=0,v=0；圆柱采用无滑移壁面边界条件(Wall)，圆柱表面流体的速度为圆柱的运动速度，即u=0,v=y˙。

2.4 网格无关性和计算方法验证

为了测试网格划分数目对计算结果的影响，选取了3 种数量的网格，分别对其在U=0.5 m/s，Re=44 700 工况下进行静止的圆柱绕流模拟计算，网格的选取和对比结果如表1 所示。在2D×2D的正方形区域内沿正方形周长和径向方向上进行网格加密，为保证计算精度，边界层网格的y+保持在30～70 范围，在模拟完一个工况后，需要查看圆柱边界网格的y+值，根据y+的大小调整圆柱第1 层网格厚度，再进行新一轮的数值模拟。

由表1 分析可知，从网格1 加密到网格2 时，CL和CD的差异率分别为5.87% 和3.78%；从网格2 加密到网格3 时，CL和CD的差异率分别为1.42%和0.67%，差异率较小，可以认为网格数量的改变对计算结果影响较小，满足网格独立性的要求。结合考虑计算资源和计算精度，最终选取网格2 作为模拟计算网格，网格2 的示意图如图4所示。

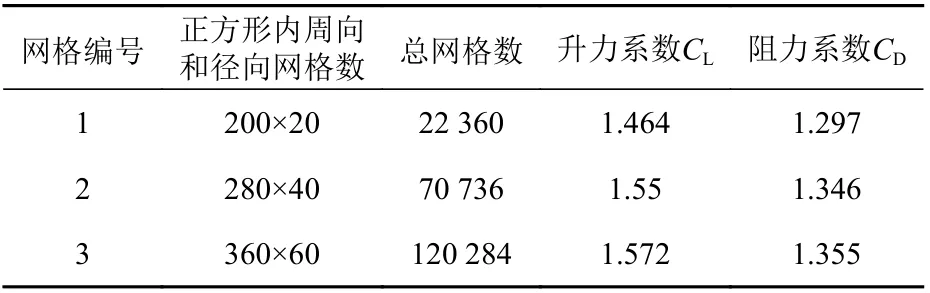
表1 网格的选取及计算结果对比Table 1 The selection of meshes and comparison of numerical simulation

图4 计算网格Fig. 4 Computational meshes

为了验证计算方法的正确性，对线性弹簧支撑的PTC 圆柱流致振动进行数值模拟，并将模拟结果和实验结果与Wu 等[13]、Ding 等[25]的计算结果作对比。图5 给出了线性弹簧下PTC 圆柱随雷诺数变化的振幅比和频率比曲线。从图5 可以看出，本文模拟方法得到的振幅比曲线成功捕捉到了初始分支、上部分支、过渡分支和驰振分支 ，频率比曲线随雷诺数变化的趋势和实验结果基本吻合，验证了本文数值模拟方法的正确性。

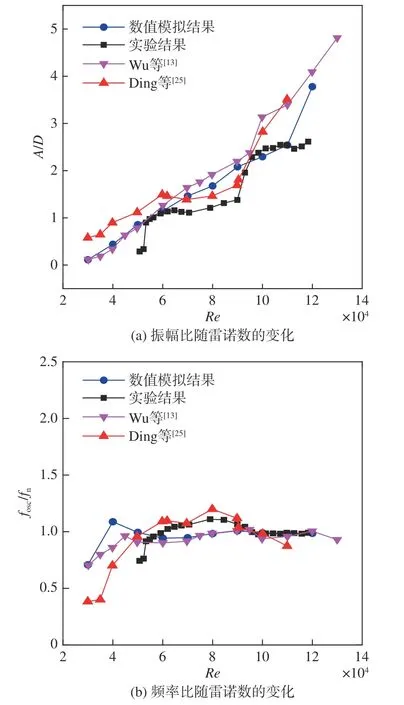
图5 线性弹簧下PTC 圆柱流致振动的数值模拟验证Fig. 5 Validation of numerical simulation of flow-induced vibrations of PTC-cylinder with linear spring

3 圆柱振动特性分析

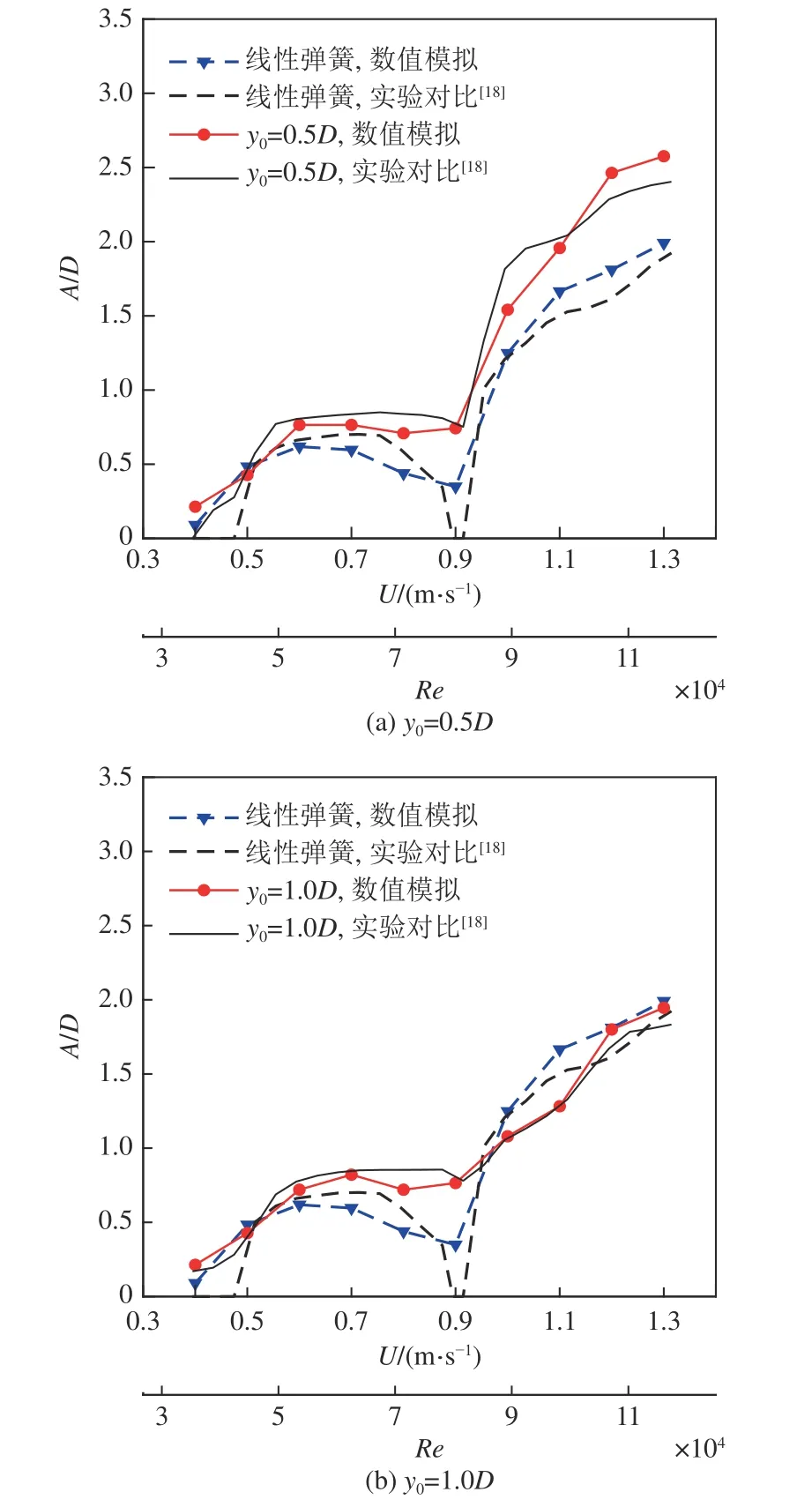
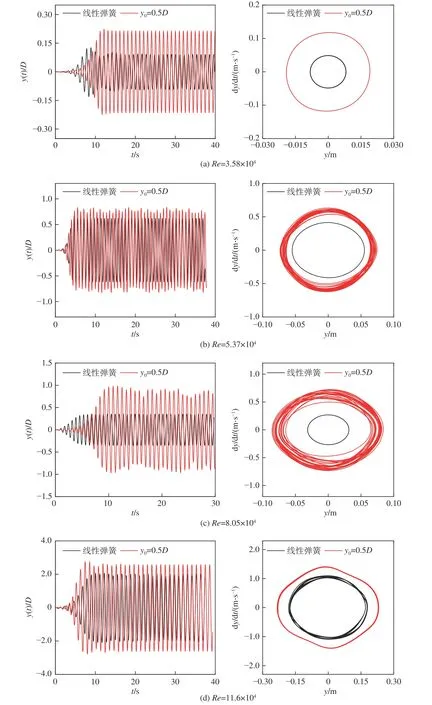
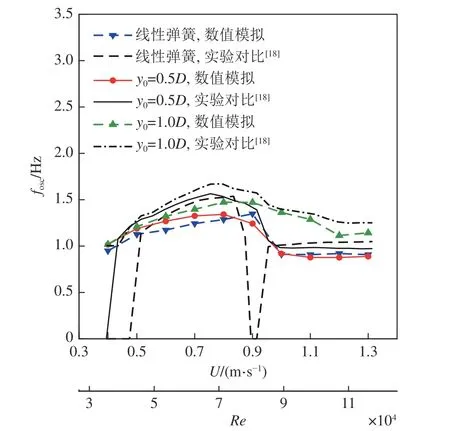
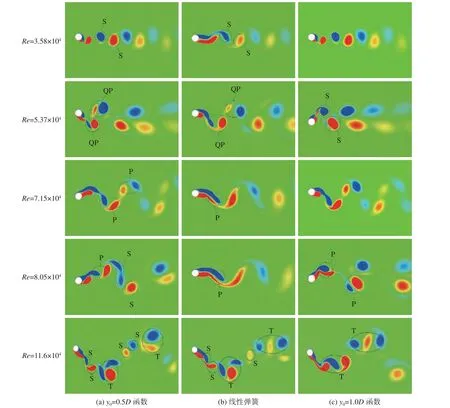
本文进行了线性弹簧和非线性弹簧下的PTC 圆柱单自由度流致振动的数值模拟，采用文献[18] 中的实验结果验证数值模拟结果。非线性弹簧刚度取K1=1 000 N/m，K2=200 N/m，阻尼ctotal=23.41 N·s/m，非线性弹簧刚度函数的分段点y0分别取0.5D，1.0D。线性弹簧刚度取K=400 N/m，阻尼ctotal=25.01 N·s/m，其他参数设置和非线性弹簧工况相同。计算的来流速度范围0.4 ～ 1.3 m/s，对应的雷诺数范围30 000

3.1 振幅响应

图6 为在不同分段函数下的PTC 圆柱流致振动的数值模拟及实验结果振幅比曲线。从图中可以看出，圆柱振动响应随雷诺数的变化大致可以划分为4 个区间：VIV 初始分支、VIV 上部分支、VIV−驰振过渡分支、驰振分支。

图6 不同分段函数下PTC 圆柱振幅比曲线Fig. 6 Amplitude ratio of the PTC cylinder for different piecewise functions

在VIV 初始分支阶段（30 000

在VIV 上部分支阶段（50 000 ≤Re< 75 000），分段弹簧下的圆柱振幅比随着雷诺数的增大保持平稳，振幅比都保持在0.730 左右。线性弹簧下的振幅比有下降的趋势，从0.596 下降到0.436，数值模拟和实验结果基本一致。同时，分段弹簧下的振幅和线性弹簧下相比偏大，y0=0.5D函数的振幅和y0=1.0D函数大致相同。

在VIV−驰振过渡阶段（75 000≤Re≤85 000），实验中线性弹簧下的圆柱基本没有振动，数值模拟的振幅比随着雷诺数的增大有所下降，下降到0.349，数值模拟捕捉的结果较为准确。实验中分段弹簧下的圆柱振幅比和线性弹簧下的相比较大，y0=0.5D函数和y0=1.0D函数的数值模拟振幅比在0.742 左右，和实验结果基本吻合。

在驰振阶段（85 000≤Re< 120 000），线性弹簧和分段弹簧下的圆柱振幅比随着雷诺数的增大而急剧增大。线性弹簧下的振幅比从1.249 增加到1.991，增大的幅度为0.742。y0=0.5D函数的圆柱振幅比由1.541 增大到2.576，增大的幅度为1.035。在Re=11.6×104时，y0=0.5D函数的圆柱振幅比比线性弹簧下的增大了29.4%。同时，y0=0.5D函数的圆柱振幅比和线性弹簧下相比整体偏大。和线性弹簧下相比，y0=1.0D函数的圆柱振幅比并未表现出增大趋势，随着雷诺数的增大，振幅比先是偏小，然后基本相同，数值模拟结果和实验结果基本吻合。

图7 给出了不同雷诺数下线性弹簧和y0=0.5D函数弹簧支撑的PTC 圆柱位移比时历曲线以及取20 s 稳定振动状态时的振动速度相图。从圆柱振动速度随位移变化的相图中可以看出，在所有的振动分支中，y0=0.5D函数弹簧的圆柱振动速度曲线包围了线性弹簧下的振动速度曲线；这说明和线性弹簧相比，y0=0.5D函数的分段弹簧可以提高圆柱的振动速度。在初始分支中，线性和非线性弹簧下圆柱的振幅比都保持不变。随着雷诺数的增大，在上部分支时，y0=0.5D函数弹簧的圆柱出现了“拍”现象，振幅比上下波动，因为圆柱振幅比超过0.5，分段弹簧中的第2 段线性弹簧开始提供回复力，2 个不同的频率相互叠加导致这一现象。在过渡分支中，y0=0.5D函数弹簧圆柱振动的不稳定性进一步增强，而线性弹簧保持小振幅的稳定振动。从图7 可以看出，在过渡分支中分段弹簧圆柱的涡脱模式发生不稳定的过渡转化，而线性弹簧圆柱脱落的旋涡相对稳定，并且有一部分相互抵消，导致了圆柱振幅的减小。随着雷诺数进一步增大，在驰振阶段，y0=0.5D函数弹簧圆柱振动稳定，线性弹簧出现了较小幅度的“拍”现象。

图7 不同雷诺数下PTC 圆柱位移比时历曲线和振动速度相图Fig. 7 Time histories and phase portraits of the PTC-cylinder at different Reynolds numbers

3.2 频率响应

图8 为在不同分段函数下的PTC 圆柱振动频率曲线。图中圆柱的振动频率fosc通过将振动位移时程曲线进行快速傅里叶变换得到。

图8 不同分段函数下PTC 圆柱频率曲线Fig. 8 Frequency of the PTC-cylinder for different functions

在VIV 初始和上部分支阶段，线性弹簧和非线性弹簧下的圆柱振动频率fosc随着雷诺数的增大而增大，从大到小排序依次为：y0=1.0D函数、y0=0.5D函数、线性弹簧。其中，y0=1.0D函数下的振动频率fosc增幅最大，从1.019 Hz 增加到1.473 Hz，数值模拟结果和实验结果基本一致。

在VIV−驰振过渡阶段，实验中线性弹簧下的圆柱未发生振动，数值模拟捕捉到的振动频率fosc=1.348Hz。y0=0.5D函数的振动频率fosc开始下降，从1.342 Hz 下降到1.243 Hz，而y0=1.0D函数的振动频率保持平稳，fosc=1.471 Hz，数值模拟和实验结果基本吻合。

在驰振阶段，线性弹簧和y0=0.5D函数的圆柱振动频率fosc随着雷诺数的增大而保持平稳，稳定在0.9 Hz 左右。y0=1.0D函数的圆柱振动频率fosc随着雷诺数的增大而逐渐减小，减小到约1.143 Hz 后保持平稳。在此雷诺数范围内，y0=1.0D函数的振动频率fosc和y0=0.5D函数相比整体偏大，在雷诺数Re=11.6×104时振动频率fosc增大了28.6%。这表明当第1 段弹簧线性刚度比第2 段弹簧线性刚度大时，振动频率的大小和分段点有关，分段点越大，第1 段弹簧刚度在流致振动过程中发挥的作用越大，圆柱振动频率也就越大。

3.3 涡脱模式

图9 为不同雷诺数下线性弹簧和分段弹簧的圆柱尾流旋涡脱落模式。

在VIV 初始分支阶段，选取流速U= 0.4 m/s，雷诺数Re=3.58×104下的圆柱振动进行尾涡结构分析。从图9 中可以看出，线性弹簧和分段弹簧下的尾流旋涡结构为2S 模式，即在一个振动周期内，圆柱尾流处脱落了两个旋转方向相反的旋涡，S 表示单个旋涡脱落。

图9 不同雷诺数下线性弹簧和分段弹簧的圆柱尾流旋涡脱落模式Fig. 9 Wake vortex of the PTC-cylinder for linear spring function and piecewise spring functions at different Reynolds numbers

在VIV 上部分支阶段，流速U= 0.6 m/s，雷诺数Re=5.37×104时，线性弹簧和y0=0.5D函数的圆柱同时脱落一个较强和一个较弱的方向相反的旋涡，这时的尾涡结构已经在朝着2P 模式发展，但还尚未成型，称为2QP 模式，P 表示一对旋转方向相反的旋涡脱落，此时y0=0.5D函数圆柱的振幅达到0.068D，超过分段点y0，第2 段线性刚度较小的弹簧开始提供回复力。而y0=1.0D函数的圆柱振幅尾涡结构为2S 模式，从单排涡结构发展成了双排涡，这是因为振幅没有达到分段点y0，回复力仅由第1 段线性刚度较大的弹簧提供。随着雷诺数增大，U= 0.8 m/s，Re=7.15×104时，分段弹簧下的尾涡结构都发展为2P 模式，这种周期性交替脱落的旋涡会产生升力作用在圆柱上，使得圆柱产生稳定的涡激振动。线性弹簧下的尾涡结构也为2P 模式，但随着时间的增加，其中一个漩涡被逐渐拉长，另一个漩涡被抵消掉，这种尾涡模式导致了圆柱的振幅减小。

在VIV−驰振过渡阶段，流速U= 0.9 m/s，雷诺数Re=8.05×104时，线性弹簧下的尾涡依然为2P 模式，两个相互抵消的旋涡损失了一部分能量，使得圆柱振幅进一步变小。y0=1.0D函数的圆柱尾部脱落的一对旋涡没有相互抵消，导致圆柱的振幅较大，尾涡模式为2P 模式。y0=0.5D函数的尾涡脱落较为复杂，圆柱从最大负位移处向最大正位移处运动过程中脱落了单个旋涡和一个拉长涡，该拉长涡是两个旋转方向相同的旋涡未分离产生的，圆柱再从最大正位移处向最大负位移处运动时，脱落了两个旋转方向相反的旋涡。和线性弹簧相比，分段弹簧下的圆柱在该阶段脱落了更多的旋涡，导致圆柱受到更大的垂直于来流方向上的升力，圆柱的振幅变得更大。

在驰振阶段，流速U= 1.3 m/s，雷诺数Re=11.6×104时，线性弹簧下的圆柱在一个振动周期内尾涡脱落模式为T+2S+T+S 模式，共有9 个旋涡脱落，其国T 代表3 个旋涡脱落。y0=0.5D函数的圆柱在1 个振动周期内为T+2S+T+2S 模式，共有10 个旋涡脱落，尾流旋涡脱落模式也更加复杂，增强了圆柱与流体的耦合作用，使得圆柱产生更加激烈的振动。而y0=1.0D函数的尾涡模态为2T 模式，有6 个旋涡脱落，这是因为在圆柱的位移相同并且超过分段点的情况下，和y0=0.5D函数相比，y0=1.0D函数的分段点较大，第1 段线性弹簧提供的回复力占总回复力比例较大，弹簧的总体刚度较大。

图10 展示了在雷诺数Re=11.6×104时y0=0.5D函数的圆柱一个振动周期T内的尾涡变化，t/T=0.200 和t/T=0.756 时刻对应圆柱的位移y=0.5D，t/T=0.253 时刻对应圆柱的位移y=−0.5D。圆柱从最大正位移处向下运动到0.5D位置过程中，脱落了3 个旋涡，由K1=1 000 N/m和K2=200 N/m的两段弹簧共同提供回复力。接着圆柱位移从0.5D运动到−0.5D处，脱落了一个旋涡，此时圆柱仅由K1=1 000 N/m提供回复力。圆柱从−0.5D位置向下运动到最大负位移处时，也只脱落了一个旋涡，到此，前半个周期内圆柱的尾涡结构为T+2S 模式。同理，后半个周期的旋涡脱落和前半个周期相同，故在一个周期内，圆柱的尾涡结构为T+2S+ T+2S 模式。

图10 Re=11.6×104时y0 = 0.5D 函数的圆柱在一个振动周期内的尾涡变化Fig. 10 Wake vortex of the PTC-cylinder within a period of oscillation for y0 = 0.5D functions atRe=11.6×104

4 结 论

本文利用FLUENT 软件针对高雷诺数下分段弹簧和线性弹簧支撑的PTC 圆柱流致振动进行了二维数值模拟研究，并对比了模拟结果和实验结果，分析了不同分段点下分段弹簧对PTC 圆柱流致振动的影响。其中，分段弹簧函数是由两段刚度不同的弹簧组成的：K1=1 000 N/m和K2=200 N/m，并且选择两个不同分段点进行分析：y0=0.5D和y0=1.0D。得到以下结论：

1） 在所研究的雷诺数范围内，y0=0.5D函数的圆柱振幅比和线性弹簧下的相比整体偏大，在Re=11.6×104时增大了29.4%。y0=1.0D函数的振幅比和线性弹簧下的相比在VIV 上部分支阶段和VIV−驰振过渡阶段有所增大，在驰振阶段并未增大。

2） 在上部分支和过渡分支中，y0=0.5D函数弹簧圆柱振动观察到了“拍”现象。和线性弹簧相比，y0=0.5D函数弹簧可以提高圆柱的振动速度。可见选择合适分段点可以有效地增大圆柱振幅，从而提高能量转换装置的转换效率。

3） 分段弹簧下的圆柱振动频率fosc都有随雷诺数的增大而出现先增大再减小最后保持稳定的趋势。分段点y0=1.0D的振动频率fosc整体比y0=0.5D的大，表明当第1 段弹簧刚度比第2 段弹簧大时，分段弹簧下的圆柱振动频率fosc的大小和分段点的选择有关，分段点越大，第1 段刚度较大的弹簧发挥的作用越多，振动频率fosc越大。

4） 在VIV 初始和上部分支阶段，线性弹簧和分段弹簧的尾涡结构大致相同。在VIV−驰振过渡阶段，分段弹簧下的圆柱有较多的旋涡产生，可以提供更多的能量，而线性弹簧下的尾涡被逐渐拉长。在驰振阶段，和线性弹簧以及y0=1.0D函数的涡脱模式相比，y0=0.5D函数的涡脱模式最为复杂，共有10 个旋涡脱落，尾涡结构为T+2S+T+2S 模式。